Paper Menu >>
Journal Menu >>
 Journal of Minerals & Materials Characteri zation & Enginee r ing, Vol. 8, No.6, pp 495-508, 2009 jmmce.org Printed in the USA. All rights reserved 495 Plane Strain Fracture Behaviour of Fabric Reinforced Hybrid Composites under varied Notch Configurations K. Mohamed Kaleemulla1*, B. Siddeswarappa2 1 Department of Mechanical Engineering, University B.D.T. College of Engineering, Davangere 577004, India 2 Department of Industrial and Production Engineering, University B.D.T. College of Engineering, Davangere 577004, India * Corresponding Author: Phone: +919844332313, E-mail: kmdkaleemulla @gmail.com ABSTRACT Utilization of fabric reinforced hybrid polymer composites has increased tremendously in many engineering fields. The present investigation is an attempt on fabric-reinforced hybrid composite laminates with different volum e fractions of the constituent mater ials; epoxy resin, plain-woven glass fabric, and textile satin fabric. Fracture toughness of a material has immense importance in the determination of the resistance of the material to crack propagation. Hence in this article, impact behaviour and fracture toughness of the laminates were investigated as per ASTM-D256 standards. Specimen configuration includes selection of different notch depths, fiber proportion and orientations. The fracture toughness has been found to increase continuously with increased volumes of glass fabric and significantly dependent on the notch size. Experimental results are validated using analysis of variance (ANOVA) technique, and found that percentage contribution of glass content is approximately 80%, while notch depth and orientation have contributed only 16%. KEY WORDS: Impact toughness, fracture toughness, glass fabric, textile satin fabric, ANOVA, Modeling. 1. INTRODUCTION Impact damage in metal was easily detected as damage starts at the impacted surface; however, damage in composites often begins on the non-impacted surface or in the form of an internal delamination. The behavior of fiber reinforced composites when impacted by a solid object was the subject of much numerical, analytical and experimental research. The penetration and perforation of targets by projectile involve highly complex processes, which  496 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 have been investigated experimentally for more than two centuries and analytically during the last two decades [1, 2]. All composite materials that exhibit a linear elastic stress-strain relationship to failure will be very sensitive to notches. Unlike metallic materials, the effects of the notch on strength will vary with the size of the notch but are relatively independent of notch geometry [3]. The subject of composite impact behavior is one of enormous complexity. A single impact event can produce several different damage modes simultaneously. These damage modes are affected by the properties of both the impactor and the laminate. The multitude of impactor and laminate variable combinations coupled with the complexity of the impact behavior has led to the vast amount of research devoted to the analysis and improvement of FRP impact performance. The hardness of the specimen as well as the geometrical shape and dimensions of notch affect the stress concentration factor. The factor of the material with higher hardness is larger than that of the material with low hardness [4, 5]. The notch root radius governs the relative elastic stress distribution near the notch root predominantly only. Both the maximum elastic stress and the notch root radius determine the yielded zone size near the notch root [6]. The severity of stress concentration initiates propagation of cracks, causing the fracture of material. Fracture in all materials, brittle or ductile, homogeneous or composites, is governed more or less by discontinuities and imperfections, such as cracks, notches, inclusions or dispersed phases [7, 8]. Damage of composite structures through impact events is perhaps one of the most important aspects of mechanical behaviour that limit the wide applications of these materials. Whilst high-energy impact loading causes complete penetration or damage that may be detectable on the surface, low-energy impact can produce extensive sub-surface delamination with little visible surface damage. The presence of internal damage was found to cause degradation in important mechanical properties. Damage due to impact substantially reduces the residual strength after impact of composite structure [9, 10]. The principal mechanism of compressive strength reduction is local buckling of the sub-laminates formed in the delaminated area [11]. In tensile loading the strength reduction mechanism is dominated by fiber fracture. For these reasons, impact damage is generally recognized as the most severe threat to composite structures [12, 13]. Impact damage consists of complex mixtures of delaminations, matrix cracking and fiber failure. Transverse impact first initiates critical matrix cracks, due to transverse shear or bending stresses, in a layer within laminated composites with a brittle matrix. Such cracks can generate delaminations immediately along the bottom or upper interface of the cracked layer, depending on the position of the layer in the laminate. Material strength may be correlated with its fracture energy, elastic modulus, and the size of the crack initiating the fracture. In this domain, the fracture toughness of the material has a major role in the determination of the fracture behaviour and resistance of the material to  Vol.8, No.6 Plane Strain Fracture Behaviour 497 crack propagation under the influence of impact load. The material cannot be used without analysing the fracture behaviour or ultimate strength of structure. In assessing the strength of a structural element, fracture mechanics provides a greater insight when a crack-like defect is explicitly taken into account. Central to the process is the determination of stress intensity factor, which is a function of the geometry of the structure and the character of the load. The advent of fracture mechanics [14-16] has accelerated the methods for determination of crack growth rate and maximum allowable damage at limit load conditions. Hence, the degradation of strength of composite materials in presence of notch must be understood precisely under any situation for the wider application. Hybrid composites are finding wide applications in numerous structures of aircraft and spacecraft, as well as other cladding situations, and thus the understanding of the fracture behaviour and prediction of fracture toughness of composite materials have assumed greater importance. One of the accepted methods of analysing fracture behaviour is the application of Linear Elastic Fracture Mechanics (LEFM) [16], where the attention is focused on exploring the fracture mechanism at the crack tip of the fibre composites. A number of methods, both experimental and analytical, have been suggested by researchers [17-19] for the assessment of fracture strength as well as life prediction of composite materials. Cantwell and Morton [20] studied the response of CFRP under low and high velocity impact and found that low velocity impact results in global deformation whereas high velocity impact results in a localized deformation. All structures from aircraft fuselages to chemical storage tanks will inevitably be subjected impacts of some type be it a dropped tool or bomb blast. Traditional laminated composites, however, perform very poorly when subjected to transverse impacts. It is therefore essential to understand the impact behavior of composites in order to properly design them. Estimating the fracture load of notched plates has more or less been established and the influence of related parameters like width and thickness of specimen, notch geometry, notch angle, notch root radius, and notch depth have widely been studied [21-23]. Thus, the determination of the stress intensity factor has become mandatory for solving the problems like residual strength analysis, fatigue crack growth rate and stress corrosion mechanism. In this article, an extensive experimental investigation is aimed at exploring the impact behavior of unstressed specimen. This study also focuses on the plane strain fracture behaviour of laminates subjected to various notch types, fiber content and orientations 2. EXPERIMENTAL 2.1 Materials Hybrid composite materials reinforced with woven fabrics are becoming increasingly popular for various structural applications in the automotive, aerospace, and other industrial sectors; particular applications of fabric-reinforced composites are in thin-walled structures. The present investigation has been carried out on three materials; epoxy resin, plain-woven glass  498 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 fabric, and textile satin fabric. The matrix material was medium viscosity epoxy resin (LY556) with a room temperature curing hardener (HY951). The plain-woven glass and textile satin fabric were the reinforcements, all the fibres in the fabric have diameters less than 30 µm. 2.2 Specimen Configuration The hybrid bi-directional composite specimen was fabricated at room temperature and under constant pressure in the shape of a rectangular plate by hand lay-up technique. Ample precautions were taken to minimise voids in the material and maintain homogeneity. Specimen preparation includes selection of different volume fractions for constituents; matrix material 40% for all samples, the volume fraction of glass fabric was between 15–45% in steps of 15% and the corresponding volume of satin fabric was estimated. The specimen preparation is in accordance with ASTM D256 dimensions, with a notch centrally located. Specimen configuration also includes selection of two fibre orientations i.e. 0/90° and ±450, for each type of the specimen five notch depths; 1, 2, 3, 4, and 5mm were cut centrally. 2.3 Instrumental Among the different testing devices, the instrumented Charpy test is very attractive since it is one of the most commonly used testing procedures. ASTM D256 standards define test conditions in order to decrease dynamic effects so that a quasi-static loading situation may be assumed. A series of medium velocity impact tests were performed on the composite specimen using single-blow pendulum type impact setup. The specimen, which was prepared earlier, was mounted and it is such that the pendulum strikes at the opposite end of the notch. 3. RESULTS AND DISCUSSION Experimentations have been carried out to characterize the candidate composite material under different loading conditions and with various specimen configurations, the analysis of the results and the influence of various parameters on the properties are summarized in the following sections. 3.1 Density Density of the laminates was measured according to the ASTM D792 standards. For density tests, rectangular samples of size 10mm X 10mm X 55mm were used with thickness and width variations of ±0.15mm and ±0.15mm, respectively. Distilled water at room temperature was used as the immersion fluid and the mass was measured using digital balance with a 10-4 g resolution. To obtain the mean value of density of each group, a total of thirty specimens such that a minimum of three specimens from each group were tested. As expected, the hybrid composites had no significant difference in density with respect to fiber orientation, this is attributed to the approximately same warp and fill count. However, the experiments show that the density of the laminates ranges from 1239.6 kg/m3 to 1649.4 kg/m3 for  Vol.8, No.6 Plane Strain Fracture Behaviour 499 laminates with increase in glass content from 15% to 45%, this is true because glass being the denser constituent among the selected materials and hence increases the sample density 3.2 Void Percentage ASTM D2734 standard was used to analyze the void percentage in composite laminate. Normally upto one percent of voids indicate a good composite, but practical difficulties increase the percentages of voids. The void content of a composite may significantly affect the mechanical properties. Higher percentages of voids usually mean lower fatigue resistance, greater susceptibility to water penetration and weathering and increased variation in strength properties. Knowing the densities of the constituents, the volume fractions of fiber, resin, and void were calculated based on two assumptions. The first assumption was that the mass of fiber in the composite was known (i.e., there is no fiber loss during manufacture). The second assumption is that the gas in any voids has the density of air, 1.29 x 10-3 g/cm3. The results show that void content varies between 2.6 to 4.8 % for laminates with different percentages of reinforcement. 3.3 Fiber Content The fiber content in the composite laminates was analyzed by using ASTM D3171 standard, this method consists of dissolving the resin portion of a weighed composite specimen in a hot digestion medium, i.e., Nitric acid. The residue is filtered, dried, and weighed. The weight percent of fiber can be converted to a volume percent of by using the fiber and resin densities. Since in this study two types of reinforcements were used, to validate the above method a second method was also used to compare the results. In the second method, fiber volume fraction of composite specimen was determined using standard method by burning small piece of hybrid composite of known weight and weighing the residue in the form of glass fibers. Comparing the results of both the tests, the deviation in volume fraction of five specimens in each case is between 0.5% to 1.1%. 3.4 Impact Behaviour of Hybrid Composite Laminates The machines with their pendulum-type hammers have been standardized including a fixed mass of the hammer and height of hammer fall, which results in a substantially fixed velocity of the hammer at the moment of impact. The striking edge of the pendulum in Charpy test, is tapered with an including angle of 450 with a radius of 3.17mm, and with an angle of fall being 141.450. According to the ASTM D256 standards, impact tests were carried on laminates, the fracture specimen geometry used in this study is the standard Charpy V-notch specimen (450 angle), with a length of 55 mm and a cross section of 10 mm X 10 mm. At mid length, a 0.25 mm root radius, 2 mm deep notch is machined. A triaxial state of stress is developed at the root of notch and hence notched specimens are used in these tests. The samples preparation includes selection of different fiber orientations and volume fraction. The specimen was clamped into pendulum impact test fixture with the notched side facing the striking edge of the pendulum. The pendulum was released and allowed to strike through the  500 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 specimen, the standards used for the investigation define test conditions in order to decrease dynamic effects so that a quasi-static loading situation may be assumed [24]. The experimental results for the standard specimen are shown in Figure 1, and from the trends, it can be clearly seen that the glass fabric content plays vital role in the impact strength of laminates. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 15 20 25 30 35 40 45 Volu me Fraction o f Glass, % I mpact St reng th, J/mm 2 0/ 90 degr ee 45 degree Figure 1. Impact Strength of laminates for various glass percentages and Orientations. Hence, it can be said that more the glass fabric percentage more will be the impact toughness and it can be observed that the impact strength has increased significantly for the increase in glass percentage, this trend is true irrespective of fiber orientation. The maximum impact toughness for 45% glass content is 0.71 J/mm2 and 0.89 J/mm2 for laminates with 0/900 and ±450 orientation respectively. The margin of increase in impact toughness for increased glass percentage is approximately same for both the orientations. However, the laminates with ±450 orientation have indicated greater impact strength compared to 0/900 fiber orientation. This is mainly due to increased number of load bearing fibers at the critical section compared to laminates with 0/900 orientation. 3.5 Effect of Notch Size on Impact Strength To analyze the effect of notch size on impact strength, hybrid composite laminates with different notch depths; 1, 2, 3, 4, and 5 mm were prepared. The specimens with various notches and volume fractions in different orientations were subjected to impact loads and the results are shown in Figure 2. The trend of reduction in impact strength for reduced glass percentage is true for all the laminates, irrespective of orientation and notch size. The higher notch depths have made the specimen to sustain lesser impact strength; this can be clearly seen from Figure 2(a) and (b), that impact toughness is large when notch depth is less and poor when depth is high. From the plots, it can be seen that the effect of notch is not that severe for 0/900 laminates with 45% glass content. Whereas the laminates with 15% glass content exhibits quite a small toughness this is attributed to the lower strength of satin fabric.  Vol.8, No.6 Plane Strain Fracture Behaviour 501 (a) Fi ber Orientation 0/90 0 0 0.2 0.4 0.6 0.8 1 54321 Notch Size, mm Impact Strength, J/mm 2 15% Glass 30% Glass 45% Glass (b ) Fi b er Orientati o n ±45 0 0 0.2 0.4 0.6 0.8 1 54321Notch Size, mm Impact Strength, J/mm 2 15% Glass 30% Glass 45% Glass Figure 2 Effect of Notch Size on Impact Strength of Composite Laminates with various Glass Percentages for (a) 0/900 Orientation and (b) ±450 Orientation. This severity of notch depth can be quite easily understandable, because as the resisting cross sectional area reduces load bearing capacity will also reduce and hence the reduction in impact toughness. The effect of notch is estimated approximately to be 10% per mm upto 3mm depth and it is 40% strength deterioration is seen for notch sizes above 3mm. 3.6 Effect of Notch Size on Fracture Toughness The results of the impact test interms of the energy are used to determine the fracture toughness of all the coupons and Figure 3 is plotted to study the effect of the notch size, glass percentage and orientation on fracture toughness. From the plots, it is evident that the trends of almost all the test coupons are approximately same with respect to the parameters under consideration. However, the fracture toughness of individual coupons is dependent on the percentage of glass content and fiber orientation. Figure 3 Effect of Notch Size and Fiber Orientation on Fracture Toughness of Composite Laminates with various Glass Percentages.  502 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 Impacted S p ecimen Fractured Side Face-2 Face-1 Fractured Layers Notch Fractured Layers Notch The results indicate that effect of notch depth is not that severe as compared to the effect of glass content and fiber orientation. For example, for a given laminate the approximate variation in fracture toughness with respect to notch size is 10% in comparison to ≈ 75% variation with respect to glass content and ≈ 30% variation based on fiber orientation. The analysis of fractured specimens reveals the catastrophic failure for all the samples, irrespective of orientation and glass content. Laminates have broken into two pieces along the notch section and in some samples the delamination due to impact is observed, this effect is comparatively more in the case of laminates with lesser glass percentage. 3.7 Failure Analysis The failure analysis is carried by analyzing the appearance of the fractured specimens, the photographs of the typical samples selected is taken. Fig.4 and 5 shows the appearance of fractured surface of specimens subjected to impact, two types of fractures was observed. In the first case laminate failed completely into two pieces, the fibers are straight indicating minimal fiber pullouts, such failure were recorded in the case of laminates with 0/900 fiber orientation as shown in Fig.4. The second type where the fiber orientation is ±450, fracture represents fiber pullouts and laminate indicated no failure in the last ply, typical sample is shown in Fig. 5. The fracture appearance is same for all the laminates irrespective of percentage of glass content. Figure 4 Fractured surfaces of impacted Composite Laminates with 0/900 fiber orientation.  Vol.8, No.6 Plane Strain Fracture Behaviour 503 Figure 5 Fractured surfaces of impacted Composite Laminates with ±450 fiber orientation. 3.8 Modeling of Impact Strength Modeling of Impact strength using Multilevel Factorial Design was used, with three factors and 36 runs. The factors selected to study the response of Impact strength are glass volume fraction, fiber orientation and Notch depth. Table 1 indicates the factors and their levels used in general linear model having 36 runs in multilevel factorial design. The Impact test results were subject to the analysis of variance. The ANOVA technique was carried out for a level of significance of 5% that is the level of confidence is 95%. For determining the significant effect of the parameters on the quality characteristics, F-test is used. Table 2 shows the results of ANOVA analysis for Impact strength. Table 1. Process parameters for Impact Response. General Linear Model: Impact Strength Versus Volume Fraction, Orientation, Hole Diameter Factor Type Levels Values Volume Fraction, % Fixed 3 15, 30, 45 Fiber Orientation, deg Fixed 2 0, 45 Notch Depth, mm Fixed 5 0, 1, 2, 3, 4, 5 Fractured Layers Face- 2 Face- 1 Notch Fractured Layers Notch  504 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 Table 2. Analysis of Variance Results for Impact Test. Source of Variation DF SS MS FCal F 0.05 P Significance Volume Fraction (VF) 2 1.6487600.824380712.204.4680.17Significant at 95% CL Fiber Orientation (FO) 1 0.1644280.164428142.055.327.99Significant at 95% CL Notch Depth (ND) 4 0.1694760.04236936.603.848.24Significant at 95% CL VF*FO 2 0.0541210.02706023.384.462.63Significant at 95% CL VF*ND 8 0.0013670.0001710.153.440.07Insignificant at 95% CL FO*ND 4 0.0092240.0023061.993.840.45Insignificant at 95% CL Error 8 0.0092600.0011580.45 Total 29 2.056637 100 SS = Sum of squares, DF = Degree of freedom, MS = Mean Square, Fcal= F-test calculated, F0.05= F-value at 5% significance level and P = Percentage of contribution. Table 2 shows the results of ANOVA analysis for Impact strength of laminates. It can be observed from the results that the interaction between the above factors does not have significant variation on the Impact strength of the composite laminates. It is clear from the ANOVA table that the glass volume fraction (p= 80.17 %), Fiber orientation (p=7.99 %) and hole diameter (p=8.24 %) have significant influence on the Impact strength. The effect of the notch depth and orientation is comparatively less, which indicates that glass volume fraction significantly controls the Impact strength of the composite laminate. However, the interaction between the factors is quite marginal and can be neglected and also the error associated in the ANOVA table was almost negligible because it is about 0.45 %. The Regression coefficient (R2) indicates that the predicted model explains 94.4% of variability in the impact strength. R2 value, which is very closer to unity, shows that the relationship between the impact strength and other factors are fairly represented by the DOE model considered for design. The main effect of the factors on impact strength can be analyzed from the Figure 6, it is clear that the glass fiber volume fraction has significant influence on Impact strength compared to other factors. The above trends generalize the effects of the factors on the impact strength, to examine individual factor with all of its levels, the detailed interaction plot for impact strength is given in Figure 7. The variation in impact strength is due to variations in the levels of the factors that are better understood by using contour and surface plots, hence to represent these effects on the impact response Figure 8 is shown below. The contour plots indicate that the highest impact strength is obtained when glass levels are high and notch depth levels are low. This area appears at the lower right corner of the plot. The surface plot also show the same response, in addition it is possible to get a general idea of impact strength at various levels of the factors.  Vol.8, No.6 Plane Strain Fracture Behaviour 505 453015 0.8 0.6 0.4 0.2 450 54321 0.8 0.6 0.4 0.2 Volume Fraction Mean Fiber O rien t atio n Not ch Dep t h Main Effects Plot fo r Impact Strength Da ta M eans Figure 6 Main Effects plot for mean Impact Strength on all factors. 0.8 0.4 0.0 54321 450 0.8 0.4 0.0 453015 0.8 0.4 0.0 Volume Fraction F ib e r Or ienta t ion Notch De pth 15 30 45 Fraction Volume 0 45 Orientation Fiber 1 2 3 4 5 Depth Notch Interaction Plot for Impact Strength Da ta M eans Figure 7 Interaction plot for Impact Strength. Volume F raction Notch Depth 45403530252015 5 4 3 2 1 > – – – < 0. 2 0.2 0.4 0.4 0.6 0.6 0.8 0. 8 Strength Impact Contour Plot of Im pact Strength vs Notch Depth, Volum e Fraction Figure 8 Contour and Surface plots for Impact Strength. 3 45 0.00 0.25 0 1 0. 50 0.75 2 1.00 3 15 4 5 Impac t S tren g th Volume Fraction Notch Depth Surface Plot of Impact Strength vs Volum e Fraction , No tch D epth 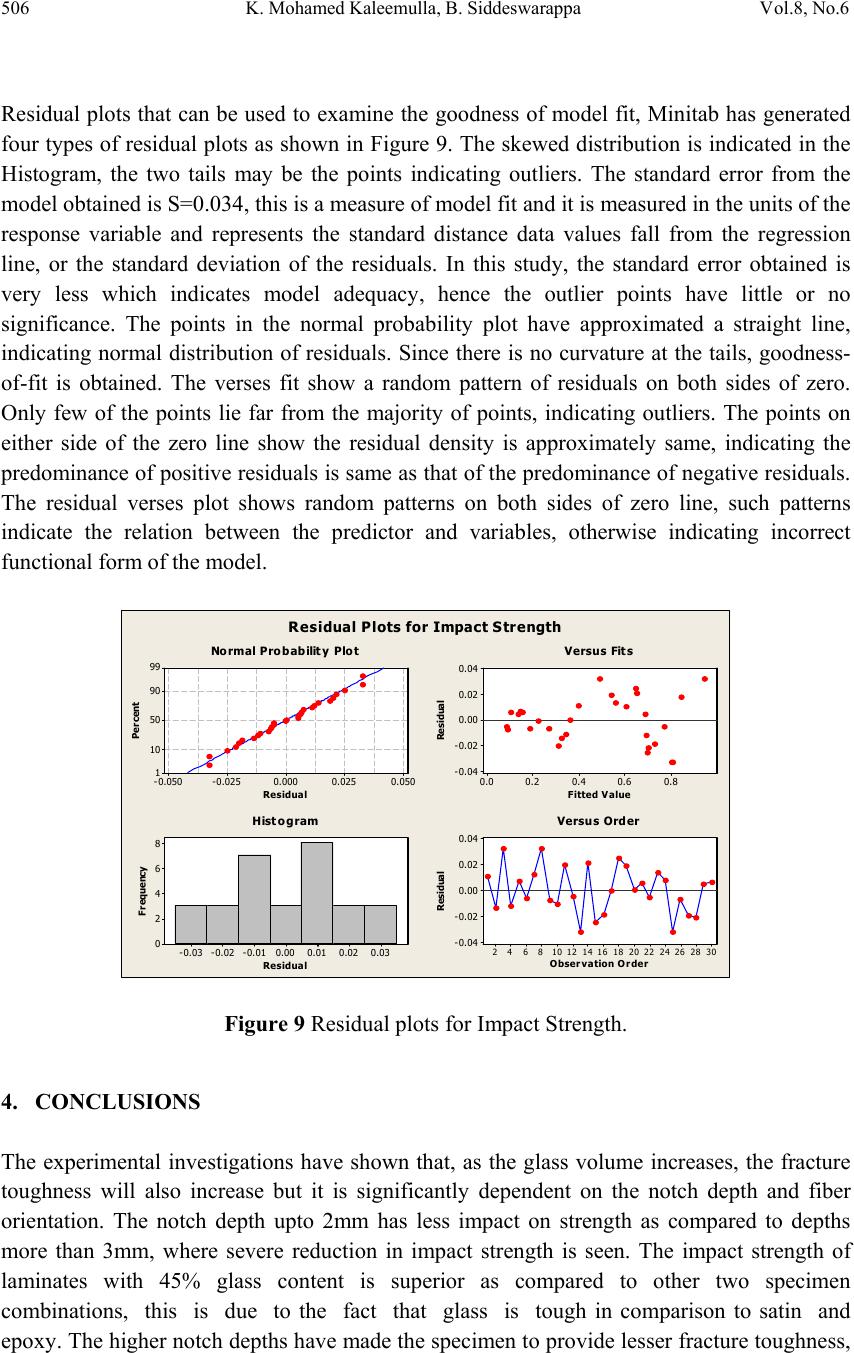 506 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 Residual plots that can be used to examine the goodness of model fit, Minitab has generated four types of residual plots as shown in Figure 9. The skewed distribution is indicated in the Histogram, the two tails may be the points indicating outliers. The standard error from the model obtained is S=0.034, this is a measure of model fit and it is measured in the units of the response variable and represents the standard distance data values fall from the regression line, or the standard deviation of the residuals. In this study, the standard error obtained is very less which indicates model adequacy, hence the outlier points have little or no significance. The points in the normal probability plot have approximated a straight line, indicating normal distribution of residuals. Since there is no curvature at the tails, goodness- of-fit is obtained. The verses fit show a random pattern of residuals on both sides of zero. Only few of the points lie far from the majority of points, indicating outliers. The points on either side of the zero line show the residual density is approximately same, indicating the predominance of positive residuals is same as that of the predominance of negative residuals. The residual verses plot shows random patterns on both sides of zero line, such patterns indicate the relation between the predictor and variables, otherwise indicating incorrect functional form of the model. 0.0500.0250.000-0.025-0.050 99 90 50 10 1 Residual Percent 0.80.60. 40.20.0 0.04 0.02 0.00 -0.02 -0.04 Fitted Value Resi dual 0.030.020.010.00-0.01-0.02-0.03 8 6 4 2 0 Residual Frequency 30282624222018161412108642 0.04 0.02 0.00 -0.02 -0.04 Observation Order Resi dual Normal Pro b abilit y PlotVersus Fit s Hist o g ramVersu s Ord er Residual Plots for Impact Strength Figure 9 Residual plots for Impact Strength. 4. CONCLUSIONS The experimental investigations have shown that, as the glass volume increases, the fracture toughness will also increase but it is significantly dependent on the notch depth and fiber orientation. The notch depth upto 2mm has less impact on strength as compared to depths more than 3mm, where severe reduction in impact strength is seen. The impact strength of laminates with 45% glass content is superior as compared to other two specimen combinations, this is due to the fact that glass is tough in comparison to satin and epoxy. The higher notch depths have made the specimen to provide lesser fracture toughness,  Vol.8, No.6 Plane Strain Fracture Behaviour 507 this behaviour is true for all volumes of glass fabric and orientations. It is reasonable to assume that the main energy absorption mechanisms are delamination and deformation including membrane and bending deformations because of fiber breakage. ANOVA technique used to validate the above discussion has supported the trends and found that the glass percentage significantly controls the impact toughness with a percentage contribution of about 80%, while the orientation and notch depth has less significance with each contributing approximately for 8%. REFERENCES 1. Backman, M. and Goldsmith, W. (1978). Int. J. of Engineering Science., 16: 1-99. 2. Zukus (1982). Penetration and perforation of solids. Impact dynamics, ed.: Wiley, 155- 214 3. MIL-HDBK-17-1F (2002). Composite Materials Handbook: Volume 1. Polymer Matrix Composites Guidelines for Characterization of Structural Materials, Department of Defense Handbook., 1: Chapter 7. 4. Taniuchi, K.(1990). The experimental analysis of yield stress at bottom of notch roots, Applied Stress Analysis., 1: 234–242. 5. Whitney, J.M. and Nuismer, R.J. (1974). Stress fracture criteria for laminated composites containing stress concentration, Journal of Computational Mathematics., 8(3): 253 6. Hyakutake, H. and Hagio, T. (1990). The severity near the notch root of notched bars, Applied Stress Analysis., 1: 243–249. 7. Lyons, J. (2003). Temperature Effects on Fractural Toughness of Polymeric Composites, Pittsburg State University-Kansas Technology Center., 27. 8. Reifsnider, K.L., Liao, K., McCormic, M. and Tiwari, A. (1997). Fibre fracture in continuous fibre ceramic composites: concepts and observations, J. of Engineering for Gas Turbine and Power., 119(1): 205. 9. Starnes, J.H., Rhodes, M.D. and Williams, J.G. (1979). Nondestructive Evaluation and Flaw Criticality for Composite Materials, ASTM STP., 696: 145. 10. Starnes, J.H. and Williams, J.G. (1982). NASA Technical Memorandum 84552, Washington DC., 157. 11. Wang, A.S.D. (1984). Composite Technology., 6: 45. 12. Greszczuk , L.G. (1975). ASTM STP., 568: 14. 13. Whitehead, R.S. (1985). Proc. of the 7th Conf. on Fibrous Composites in Structural Design, AFWAL-TR., 85-3094: 331-352. 14. Chell, G.G. (1979). Developments in Fracture Mechanics–1, Applied Science Publication Ltd., London. 15. Broke, D. (1987). Elementary Engineering Fracture Mechanics, 4th ed., Martinus Nijhoff Publishers, The Netherlands., 16. Hyakutake, H., Nisitani, H. and Hagio, T. (1989). Fracture criterion of notched plates of FRP, J. of Japan Society of Mechanical Engineers., 32(2): 300. 17. Konish, H.J. and Cruse, T.A. (1975). Determination of fracture strength in orthotropic graphite/epoxy laminates, Composite Reliability, ASTM STP., 580: 490.  508 K. Mohamed Kaleemulla, B. Siddeswarappa Vol.8, No.6 18. McClintock, F.A. and Irwin, G.R. (1984). Plasticity Aspects of Fracture Mechanics in Fracture Toughness Testing and it’s Applications, ASTM STP., 381: 84. 19. O’Brien, T.K., Johnson, N.J., Morris, D.H. and Simonds, R.A. (1982). A simple test for the interlaminar fracture toughness of composites, SAMPE Journal., 18(4): 8–15. 20. Cantwell, W.J. and Morton, (1989). The influence of varying projectile mass on the impact response of CFRP, Composite Structures., 13: 101-114. 21. Awerbach, J. and Madhukar, M.S. (1985). Notched strength of composite laminates: predictions and experiments – a review, J. of Reinforced Plastics and Composites.,4: 105. 22. Pipes, R.B., Wetherhold, R.C. and Gillespie Jr., J.W. (1979). Notched strength of composite materials, J. of Composite Materials., 12: 148. 23. Weixing, Y. 1992). On the notched strength of composite laminates, J. of Composite Science and Technology., 45: 105. 24. Rittel, D., Pineau, A., Clisson, J. and Rota, L. (2002). On Testing of Charpy Specimens Using the One-point Bend Impact Technique, Experimental Mechanics., 42: 1-6. |

