Paper Menu >>
Journal Menu >>
 Journal of Minerals & Materials Characterization & Engineering, Vol. 8, No.6, pp 417-425, 2009 jmmce.org Printed in the USA. All rights reserved 417 Mathematical Model for Optimizing Charge and Heel Levels in Steel Remelting Induction Furnace for Foundry Shop O.K. Abubakre and R.A. Muriana* Mechanical Engineering Department, Federal University of Technology, Minna, Nigeria *Corresponding Author: mraremu@yahoo.com Abstract Heat energy balance equation in an induction furnace was developed along with computer programme (model) written in basic programming language to optimize the charge/heel level in the furnace, using the hypoeutectic AISI-SAE 1042 alloy steel as charge material. Time and cost of electrical energy consumption were considered as the decision variables. The model results showed that Charge (solid scrap) and Heel (molten steel) levels of ratio 3:2 was the optimum for an economical productivity. 1. INTRODUCTION Considerable amount of rejects at the end of a production line in an alloy steel based plant, turnings and borings from machine shops, trimmings from die forging, sprue, risers and gates from foundry shops, all could constitute scrap piles which could be remelted and reused in production line. Induction furnace is found suitable in achieving this aim because of its traditional moderate size and environmental friendliness, making its movement easy. The heat needed to generate melt is itself generated within the scrap electromagnetically- a non-contact heating process. High frequency electricity drives a large alternating current through a coil which in turn generates a very intense and rapidly changing magnetic field (causing eddy current in the scrap). In other to achieve time-gain melting exercise, part of the subsequent melt is left in the furnace as “heel” to preheat the next charged solid scrap. This work is aimed at determination of most economic, optimum, level of charge and heel in the routine melting.  418 O.K. Abubakre and R.A. Muriana Vol.8, No.6 1.1. Literature Review 1.1.1. Electromagnetic induction heating Induction heating is mainly dependent on two physical phenomena: 1. Faraday-Lenz’s law and 2. The Joule effect When loop of a conductor is placed in an alternating magnetic field, alternating current is induced in the loop thus E = dt d Φ (1) Where E = voltage (v) Φ = magnetic flux (wb) t = time (s) Faraday affirmed that when this loop is short-circuited, the induced voltage ‘E’ will cause current to flow and oppose its cause, the alternating magnetic field. If a massive conductor (like a charged crucible) is placed in the alternating magnetic field, eddy current will be induced and in turn, generate heat within the conductor according to the joule effect principle. [1] 1.1.2. The Joule effect When current ‘I’ (A) flows through a conductor with resistance ‘R’ (Ω), power ‘p’ (w) is dissipated in the conductor as [2]: P = R x I 2 1.1.3. Skin effect A source of high frequency electricity is used to drive a large alternating current through the coil. This coil is known as the work coil (Figure 1). The passage of current through this coil generates a very intense and rapidly changing magnetic field in the space within the work coil. The work piece to be heated is placed within this intense alternating magnetic field. The alternating magnetic field induces a current flow in the conductive work piece. The arrangement of the work coil and the work piece can be thought of as an electrical transformer. The work coil is like the primary where electrical energy is fed in, and the work piece is like a single turn secondary that is short-circuited. This causes tremendous currents to flow through the work piece. These are known as eddy currents.(Figure 2). In addition to this, the high frequency used in induction heating applications gives rise to a phenomenon called skin effect. This skin effect forces the alternating current to flow in a thin layer towards the surface of the work piece. The  Vol.8, No.6 Mathematical Model for Optimizing Charge and Heel Levels 419 skin effect increases the effective resistance of the metal to the passage of the large current. Therefore it greatly increases the heating effect caused by the current induced in the work piece. So, the skin effect is characterized by a parameter called penetration depth (δ in mm) to estimate the induced eddy current penetration depth. Maxwell’s equation gives δ as f k r µ ρ δ = (2) Where ‘ρ’ = electrical resistivity (Ω.m) µ r = relative magnetic permeability (H/m) f = frequency (Hz) and k = proportionality constant (503 for steel) [3] Figure 1. Skin effect demonstration on the surface of the heated bolt(www.inductionheating.co.uk ) Figure 2: Eddy current concentrates on the surface of the work piece  420 O.K. Abubakre and R.A. Muriana Vol.8, No.6 1.2. Induction Furnace Heat Generation 1.2.1. Heat generation rate in an induction furnace The heat ‘Q’ in joule, generated in an induction furnace is directly proportion to the square of the induced current ‘I s ’ in Ampere, as shown in equation 3. tfIZQ rs •= )( 2 ρµ (3) Heat generation rate is therefore given by t Q where Z = an empirical constant [4]. The induction furnace arrangement behaves likes a transformer. The work coil is likened to the primary winding while the charge serves as secondary winding [5]. 1.2.2. The Heat (H s ) needed to melts solid scrap of mass m s in Kg and raise the melt temperature from ambient temperature to a superheat temperature θ s in o C. Heat H s shall be the addition of heat to raise the scrap’s temperature from ambient temperature to its melting point, heat needed to change the solid scrap to liquid at the same temperature and the heat needed to raise the temperature of the melt from melting point to a given superheat temperature. Thus, )()( msssmss CmLmCmH θθθθ −++−= (4) Where C = specific heat capacity of the scrap material in …. m θ = melting point of the scrap material θ = ambient temperature The heat contents of heel and the mixture (solid scrap and heel) are connoted as H h and H mx respectively (equation 5 and 6) )( mshhmhh CmLmCmH θθθ −++= (5)  Vol.8, No.6 Mathematical Model for Optimizing Charge and Heel Levels 421 mxhsmx CmmH θ )( += (6) (The resulting mixture is assumed to be is solid form, else the model does not apply). Similarly, H mx can be written as += θ CmH smx )( mshhmh CmLmCm θθθ −++ Then, )( sh shhs mx mmC CmLmCm + ++ = θθ θ (7) Where θ mx = mixture’s temperature. The crucible effective mass m eff = m s + m h . 2. THE MODEL EQUATIONS Assumptions: 1. Heat loss during opening and closing of the furnace is neglected 2. The heat absorbed by the crucible (during the first melting) is not accounted for. To have a complete melt from the scrap, the inductive heat generated by the furnace must be equal to the heat needed to melt the scrap. Therefore, Q = H s . That is, tfIZ rs •)( 2 ρµ = )()( msssms CmLmCm θθθθ −++− (8) And t = )( )()( 2 fZI CmLmCm rs msssms ρµ θθθθ −++− (9) 3. THE MODEL PROGRAM CLS 10 REM “MODEL PROGRAMME FOR OPTIMIZING SCRAP –HEEL LEVEL IN STEEL REMELTING INDUCTION FURNACE USING STEEL GRADE AISI-SAE 1042 AS THE CHARGE MATERIAL  422 O.K. Abubakre and R.A. Muriana Vol.8, No.6 20 DIM M heel (200), M scrap (200),T mx (200),Q m (200), COST s (200),COST h (200),G(200),T hr (200) 35 DIM Q 1 (200), Q 2 (200), Q 3 (200),C s (200),C t (200),C h (200),C sh (200),COST s 1Kg(200) 40 DIM COST h 1Kg (200), COST melt (200), G (200), J (200), Pp (200), NS (200), LS(200) 50 REM “ ρ S ” IS CHARGE MATERIAL DENSITY; “V cru ” AND “V eff ” ARE TOTAL AND EFFECTIVE VOLUMES IN RESPECTIVELY 55 REM “M eff IS EFFECTIVE MASS OF CHARGE” 60 INPUT “CHARGE DENSITY =” ; ρ S 70 V cru = 0.003825: V eff = (3/4)*V cru : M eff = ρ al * V eff 75 PRINT “EFFECTIVE MASS = “ ; M eff a$ = INPUT$(1) 80 REM “C” IS SPECIFIC HEAT CAPACITY OF THE STEEL; “L” IS LATENT HEAT OF FUSION OF THE STEEL AS WELL” 90 REM “T amb ” IS THE AMBIENT TEMPERATURE; “T m ” IS MELTING POINT OF THE ALLOY (THE STEEL); AND“T s ”IS THE SUPERHEATTEMPERATURE 100 INPUT “C=”; C 105 INPUT “L” ; L 110 INPUT “T amb =”; T amb 115 INPUT “T s =”; T s 120 REM “I P ” IS THE SUPPLIED CURRENT IN AMP. ; “V P ”IS THE SUPPLIED VOLTAGE IN VOLT AND “ µ r” THE ALLOY’S RELATIVE MAGNETIC PERMIABILITY,“F”IS FREQUENCY AND“LS”IS THE INDUCED CURRENT 125 I P = 16.3: V P = 170: µ r =180: F = 50: KT = 0.0013 130 REM HEEL RANGES FROM 10% TO 50% STEP 5 WHILE SCRAP RANGES FROM 90% TO 50% STEP 5 135 REM “R sc ” IS SCRAP RANGE; “R heel ” IS HEEL RANGE; “M heel ” IS MASS OF HEEL; “M scrap ” IS MASS OF SCRAP a$ = INPUT$(1) 140 I=1 145 R sc = 0.9 150 FOR R heel = 0.1 TO 0.50 STEP 0.05 155 M heel = M eff * R heel 160 M scrap = M eff *R sc 165 Q 1 = M scrap *C* T amb 170 Q 2 = M heel * L 175 Q 3 = M heel *C * T s 180 Tmx = (Q 1 +Q 2 +Q 3 )/ (C * M eff ) 185 G = KT* (LS) ^2 205 IF Tmx >200 AND Tmx < 250 THEN PC = 0.296 ELSE IF Tmx >250 AND Tmx < 350 THEN PC = 0.301 ELSE IF Tmx >350 AND Tmx < 400 THEN PC = 0.493 ELSE  Vol.8, No.6 Mathematical Model for Optimizing Charge and Heel Levels 423 IF Tmx >400 AND Tmx < 500 THEN PC = 0.638 ELSE IF Tmx >500 AND Tmx < 600 THEN PC = 0.739 ELSE IF Tmx >600 AND Tmx < 700 THEN PC = 0.894 ELSE IF Tmx >700 AND Tmx < 800 THEN PC = 1.06 ELSE IF Tmx >800 AND Tmx < 900 THEN PC = 1.093 ELSE IF Tmx >900 AND Tmx < 1000 THEN PC = 1.11 ELSE IF Tmx >1000 AND Tmx < 1100 THEN PC = 1.142 ELSE IF Tmx >1100 AND Tmx <1200 THEN PC = 1.169 ELSE 295 a$= INPUT$(1) 208 J = ( µ r * PC* F ) ^ 0.5 210 Pp = G*J 213 t = ((M scrap *C*1350) + (M scrap *L) + (M scrap *C*125))/Pp 215 REM “T hr IS THE TIME REQUIRED IN HOUR TO MELT THE SCRAP” 220 T hr = t / 3600 225 REM “NEPArate IS COST IN NAIRA PER KWh” 230 REM “Q m IS THE ENERGY USEDE TO MELT SCRAP IN KILOWATT” 235 Q m = (I p * V p *T hr )/1000 240 NEPArate = 6 245 REM “COSTs” IS OF MELTING SCRAP 250 COST S = 6 * Q m 255 COSTs1Kg = COSTs/M scrap 260 PRINT “COST OF MELTIN 1Kg SCRAP”; “=”; COSTs1Kg 265 PRINT “MASS OF SCRAP IN Kg=”;M scrap 270 PRINT “MASS OF HEEL IN Kg=”;M heel 275 PRINT “TIME TAKEN TO MELT THE SCRAP IN HOUR=”; T hr 280 PRINTS “TEMP. OF THE CHARGE Tmx IN DEGREE CELCIUS = ”; Tmx 283 I=I+1 285 Rsc =R sc – 0.5 289 PRINT “ ” 290 NEXT R heel a$=INPUT$(1) 295 END RUN COST OF MELTING 1Kg SCRAP = 0.88 MASS OF SCRAP IN Kg = 19.1 MASS OF HEEL IN Kg = 3.38 TIME TAKEN TO MELT THE SCRAP IN HOUR = 1.01 TEMP. OF THE CHARGE Tmx IN DEGREE CELCIUS = 301.93 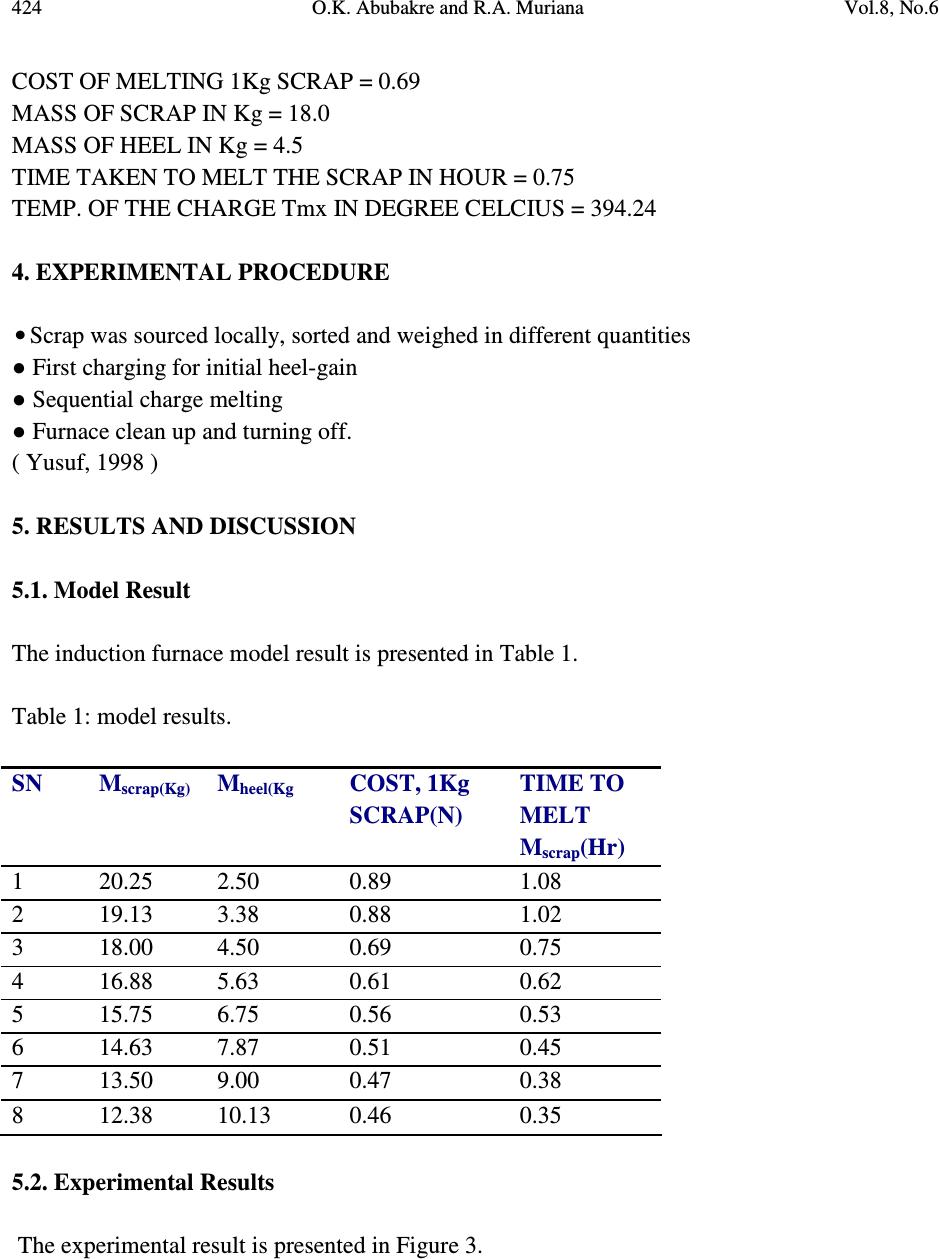 424 O.K. Abubakre and R.A. Muriana Vol.8, No.6 COST OF MELTING 1Kg SCRAP = 0.69 MASS OF SCRAP IN Kg = 18.0 MASS OF HEEL IN Kg = 4.5 TIME TAKEN TO MELT THE SCRAP IN HOUR = 0.75 TEMP. OF THE CHARGE Tmx IN DEGREE CELCIUS = 394.24 4. EXPERIMENTAL PROCEDURE • Scrap was sourced locally, sorted and weighed in different quantities ● First charging for initial heel-gain ● Sequential charge melting ● Furnace clean up and turning off. ( Yusuf, 1998 ) 5. RESULTS AND DISCUSSION 5.1. Model Result The induction furnace model result is presented in Table 1. Table 1: model results. 5.2. Experimental Results The experimental result is presented in Figure 3. SN M scrap(Kg) M heel(Kg COST, 1Kg SCRAP(N) TIME TO MELT M scrap (Hr) 1 20.25 2.50 0.89 1.08 2 19.13 3.38 0.88 1.02 3 18.00 4.50 0.69 0.75 4 16.88 5.63 0.61 0.62 5 15.75 6.75 0.56 0.53 6 14.63 7.87 0.51 0.45 7 13.50 9.00 0.47 0.38 8 12.38 10.13 0.46 0.35  Vol.8, No.6 Mathematical Model for Optimizing Charge and Heel Levels 425 12. 75 12. 80 12. 85 12. 90 12. 95 13. 00 010 20 3040 50 60 Percentage Heel Productivity (Kg/min) Figure 3. Percentage Heel against Productivity 5.3. Results Discussion The productivity increased with increase in heel level. Above 36.8% heel level however, a steep decline in productivity set in (Figure 3). From the model result (table4.1), increase in heel level up to 9.00Kg caused remarkable reduction in energy-cost of melting. Further increase above this level however caused no significant reduction in energy-cost of melting. 6. CONCLUSION Optimum range of melting the medium carbon steel in term of charge/heel ratio is between 3: 2 and 6.3: 3.7 by mass. REFERENCES 1. Callebant L. (2007) “Induction Heating”. Pp2-9. www.induction .com. 2. Theraja B.L. and Theraja A.K. (2002) “Electrical Technology” S.chand New Delhi. 926pp;Pp1479-1490 3. Sybil P.P., Jonathan W. and Betty R. (1982) “Encyclopedia of Science and Technology” Mc Graw-Hill New York 608pp, vol 3; 432pp vol 12 4. Rock H. (2003) “Induction Heating Plus” Thermal corporate, Pp1-3 5. www.inductionheating.co.uk 6. Yusuf J.A. (1998) “investigation on the effect of cold charge and heel on the productivity of foundry furnace and effect on the quality of product” Pp6-28 |

