Journal of Minerals & Materials Characterization & Engineering, Vol. 8, No.3, pp 203-221, 2009
jmmce.org Printed in the USA. All rights reserved
203
Predicting Viscosity of Limestone–Water Slurry
Pradipta Kumar Senapati*
a
, Dibakar Panda
b
, Ashutosh Parida
a
a
Institute of Minerals & Materials Technology (IMMT), Bhubaneswar-751013, India
b
Department of Chemical Engineering, C.V.Raman College of Engineering,
Bhubaneswar-752054, India
* Corresponding author: [e-mail], [e-mail]
ABSTRACT
The rheological behavior of limestone–water slurry samples was investigated for different
volume concentrations, particle size distribution and slurry temperature. Experiments were
conducted over a range of volumetric solids concentration (
=
φ
0.20- 0.46) in shear rate range
of 1-300 s
-1
. The slurry showed Newtonian behavior up to a volumetric solids concentration of
37.8 vol. %, beyond which the slurry was highly pseudoplastic in nature and fitted excellently to
a non-Newtonian Power law model. The relative viscosity (
r
η ) of the mixture slurry, defined as
the suspension viscosity over the viscosity of the suspending medium was found to be increasing
exponentially when
φ
exceeds 0.404. By adopting an experimental approach, the rheological
data indicated that
φ
might reach 0.462. Using the (
21
1
−
−
r
η ) -
φ
relationship proposed by Liu,
the theoretical maximum solids fraction (
m
φ ) was evaluated as
m
φ = 0.504 for the given slurry
samples and was then used to predict the relative viscosity (
r
η ) by some existing models. Five
empirical models namely; Liu, Dabak et al., Krieger-Dougherty, Mooney and Chong et al. were
considered for the purpose. Liu’s model better predicted the relative viscosity and thus would be
helpful in evaluating the hydraulic parameters accurately for design of limestone slurry
pipelines operating at high concentrations.
Keywords: Limestone-water slurry, Relative Viscosity, Maximum solids concentration

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 204
1. INTRODUCTION
The steel industries require limestone as a fluxing agent in huge quantity, both in the blast
furnace and steel melting shop. Commercial hydraulic transportation of limestone from the mine
site to the steel industries can be an economically viable technology. Therefore, it is essential to
formulate highly dispersed homogeneous slurry of ground limestone powder in water medium
for hydraulic transportation through pipelines. The slurry rheology is required to be studied for
evaluating the various hydraulic parameters such as optimum transport concentration, design
velocity, pumping power, specific power consumption etc [1].
The rheology behavior of the slurry is essentially to be controlled in many industrial processes
such as transportation of slurries, dewatering and wet grinding [2]. A number of theoretical and
empirical equations have been developed to predict the viscosity of concentrated suspensions [3,
4]. Each equation has achieved some agreement between prediction and measurement, but with
limits to factors such as solids concentration and powder characteristics, in a variety of
suspension systems.
Studies conducted on the rheological behavior of iron powder (average particle size was 28.48
µ
m) suspensions with some binders indicated that the dynamic viscosity increased with
increasing solid content due to strong interaction between particles [5]. The rhological behavior
of calcite suspensions behaved as a shear thinning fluid with a yield value, and the viscosity
increases when the particle size decreases due to attractive interparticle forces [6] . Experimental
investigation on the rhelogical behavior of highly concentrated zirconia-wax mixtures implied
that an optimal temperature control is very much essential for preparation of such mixture slurry
for injection molding [7, 8]. A model was also proposed by Liu [9] to predict the maximum
particle packing density (
m
φ ) over a wide variety of ceramic suspensions through the use of a
few viscosity-concentration data. By applying the Liu’s model, the maximum solid loading
m
φ of
barium titanate (BaTiO
3
) aqueous suspensions was evaluated according to a linear
φη −−
−
)1(
21
r
relationship [10, 11]
Various physical and chemical properties of a slurry, such as solids concentration, particle size
distribution, shear rates, temperature etc. have significant influences on the slurry rheology due
to change or modification in surface property [12]. The investigation on the rheological behavior
of limestone slurries (d
50
=24.68µm) indicated pseudoplastic behavior at higher concentrations.
The maximum packing solids fraction )(
m
φ was predicted as 6.64 =
m
φ vol. % for the slurry with
the addition of a polymeric dispersant [13]. However from commercial application point of view,
a semi-empirical approach will be of great importance in determining the maximum packing
solids fraction )(
m
φ from rheological data without addition of additives.

205 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
In literature, the value of
m
φ , is considered as one of the most important parameters in describing
the rheological properties of the slurry. In this paper, we aimed to investigate the rheological
behavior of the limestone-water slurry to relate
φ
with
r
η and try to estimate
m
φ . The value of
maximum solids fractions were determined experimentally and theoretically without application
of any dispersant. By applying the various theoretical and empirical models, the relative
viscosity of the slurry under given solids fractions were predicted using the maximum solids
fraction
m
φ determined from the
r
η -
φ
relationship. Also the effect of particle size distribution
and temperature on the relative viscosity of the lime stone slurry has been investigated.
2. EXPERIMENTAL
2.1. Raw materials
The limestone sample used for the study was procured from Purnapani limestone mines, Orissa
situated around 30 km away from Rourkela Steel Plant. The raw samples of size 5 mm was dry
ground in a ball mill and 2 product samples designated as S-1 and S-2 with different milling
time intervals were taken for the study. The size distribution of the two samples S-1 and S-2 was
measured in a Malvern PSD analyzer and the d
50
of the samples were determined to be 26.31 µm
and 53 µm respectively. The particle size distribution is shown in Fig.1. This has been finely
ground taking into consideration the liberation characteristics of inorganic constituents present in
it. The density of the sample has been determined with 50 ml standard specific gravity bottle.
The density of the sample is 2.743g/cm
3
. The chemical analysis of the sample was done by
standard methods and is given in Table 1.
Table 1. Complete Chemical analysis of limestone samples
Main chemical composition Percent (%)
CaO
MgO
SiO
2
Al
2
O
3
Fe
2
O
3
TiO
2
P
2
O
5
SO
3
K
2
O
Na
2
O
Loss of Ignition (LOI)
47.7
4.9
6.1
3.38
0.72
0.002
0.089
0.024
0.55
0.16
36.89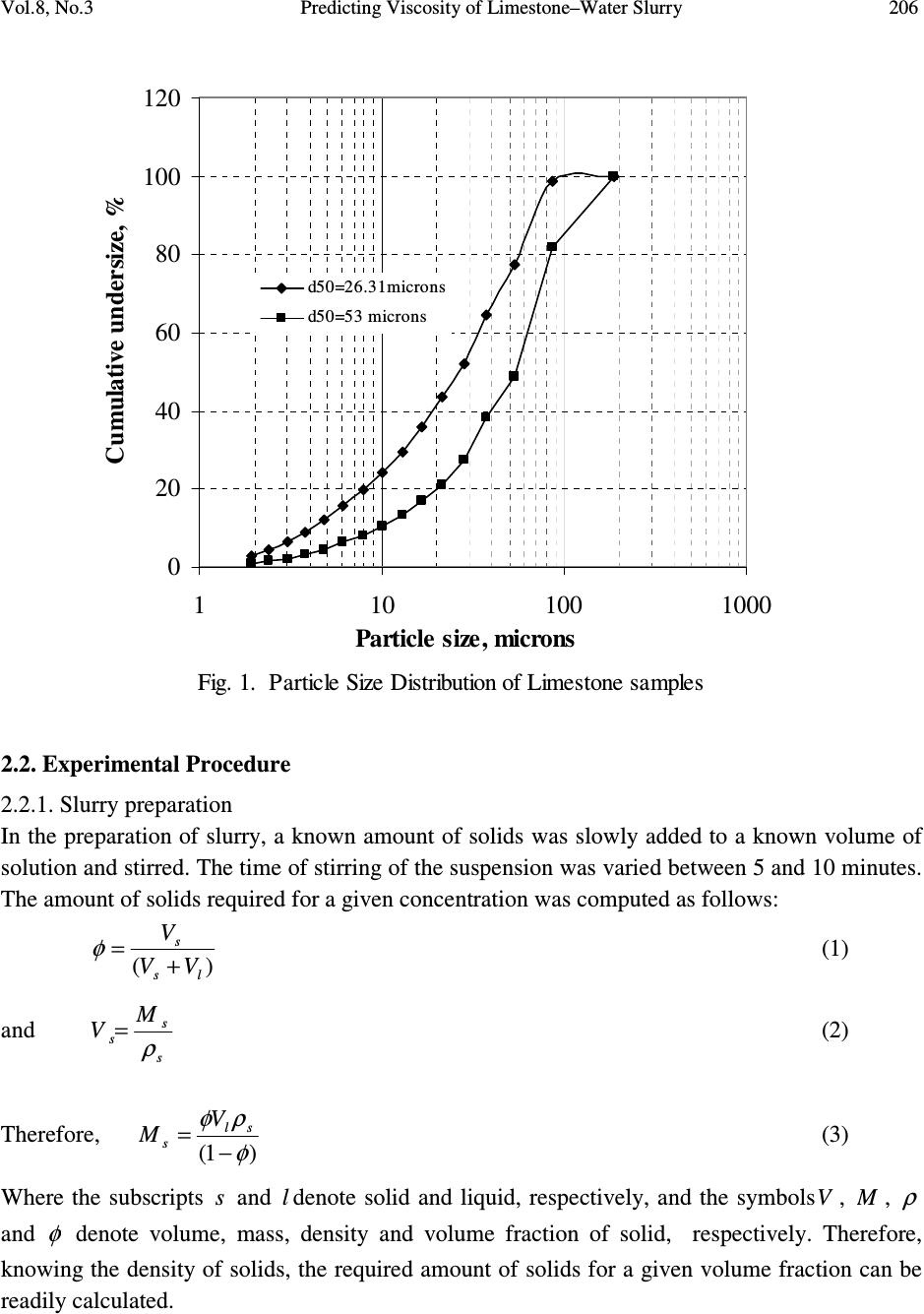

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 206
Fig. 1. Particle Size Distribution of Limestone samples
0
20
40
60
80
100
120
110100 1000
Particle size, microns
Cumulative undersize, %
d5 0=26.31 mic r on s
d50=53 microns
2.2. Experimental Procedure
2.2.1. Slurry preparation
In the preparation of slurry, a known amount of solids was slowly added to a known volume of
solution and stirred. The time of stirring of the suspension was varied between 5 and 10 minutes.
The amount of solids required for a given concentration was computed as follows:
)(
ls
s
VV
V
+
= φ (1)
and
s
s
s
M
V
ρ
= (2)
Therefore,
)1( φ
ρφ
−
=
sl
s
V
M (3)
Where the subscripts
s
and l denote solid and liquid, respectively, and the symbols V ,
M
,
ρ
and
φ
denote volume, mass, density and volume fraction of solid, respectively. Therefore,
knowing the density of solids, the required amount of solids for a given volume fraction can be
readily calculated.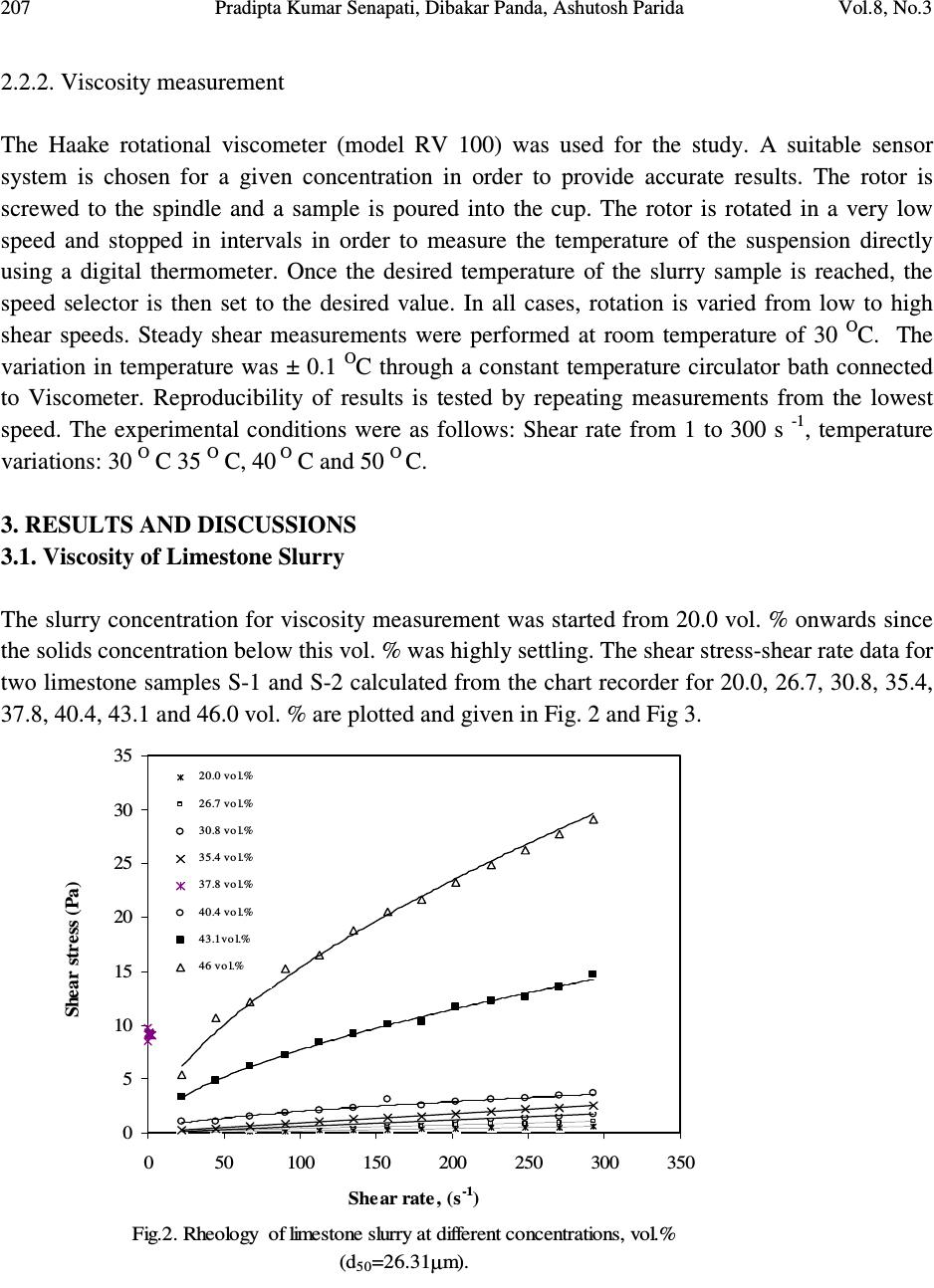

207 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
2.2.2. Viscosity measurement
The Haake rotational viscometer (model RV 100) was used for the study. A suitable sensor
system is chosen for a given concentration in order to provide accurate results. The rotor is
screwed to the spindle and a sample is poured into the cup. The rotor is rotated in a very low
speed and stopped in intervals in order to measure the temperature of the suspension directly
using a digital thermometer. Once the desired temperature of the slurry sample is reached, the
speed selector is then set to the desired value. In all cases, rotation is varied from low to high
shear speeds. Steady shear measurements were performed at room temperature of 30
O
C. The
variation in temperature was ± 0.1
O
C through a constant temperature circulator bath connected
to Viscometer. Reproducibility of results is tested by repeating measurements from the lowest
speed. The experimental conditions were as follows: Shear rate from 1 to 300 s
-1
, temperature
variations: 30
O
C 35
O
C, 40
O
C and 50
O
C.
3. RESULTS AND DISCUSSIONS
3.1. Viscosity of Limestone Slurry
The slurry concentration for viscosity measurement was started from 20.0 vol. % onwards since
the solids concentration below this vol. % was highly settling. The shear stress-shear rate data for
two limestone samples S-1 and S-2 calculated from the chart recorder for 20.0, 26.7, 30.8, 35.4,
37.8, 40.4, 43.1 and 46.0 vol. % are plotted and given in Fig. 2 and Fig 3.
Fig.2. Rheology of limestone slurry at different concentrations, vol.%
(d
50
=26.31µm).
0
5
10
15
20
25
30
35
050100 150 200 250 300 350
Shear rate, (s
-1
)
Shear stress (Pa)
20.0 vol.%
26.7 vol.%
30.8 vol.%
35.4 vol.%
37.8 vol.%
40.4 vol.%
43.1 vol.%
46 vol.%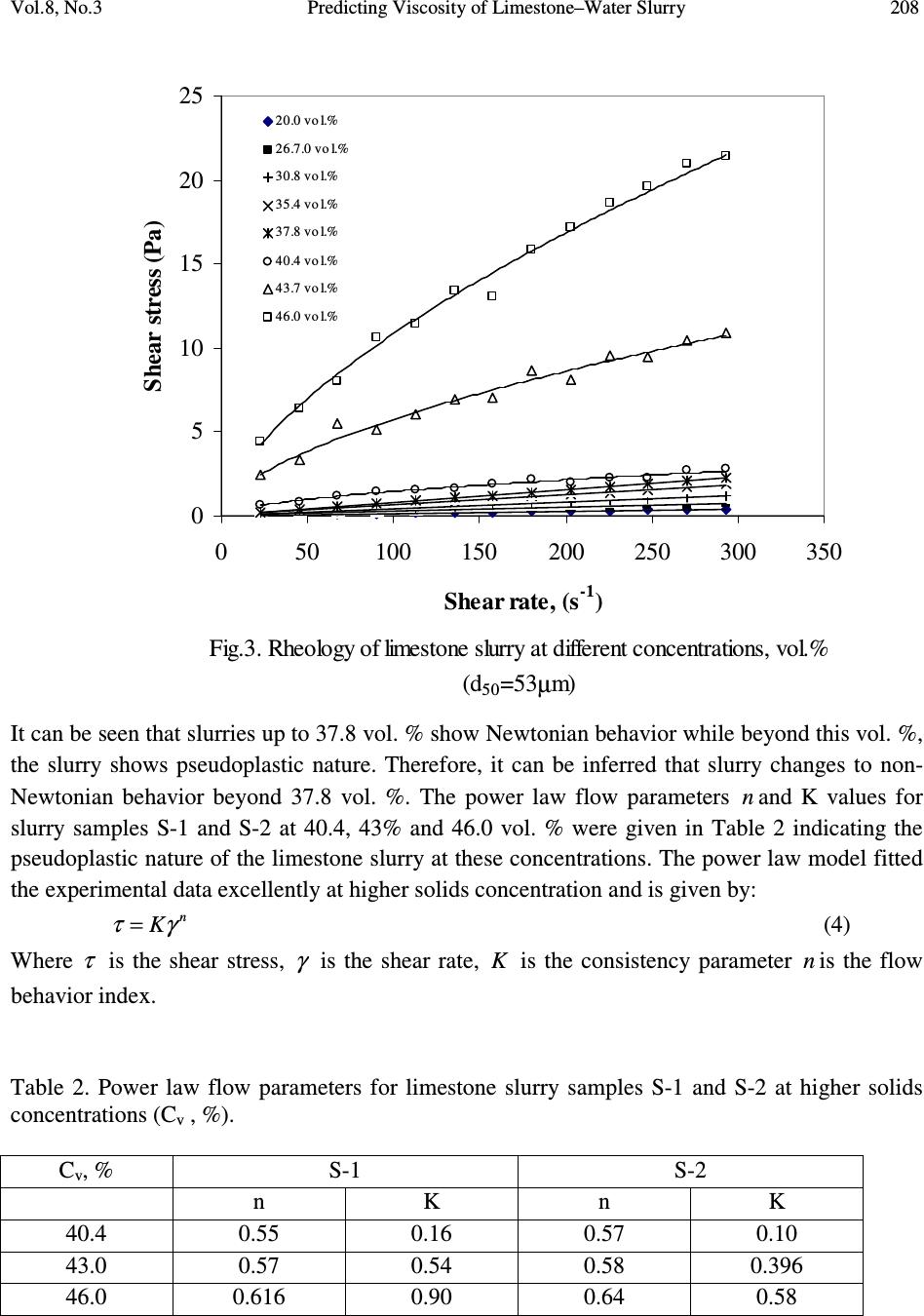

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 208
Fig.3. Rheology of limestone slurry at different concentrations, vol.%
(d
50
=53µm)
0
5
10
15
20
25
050100 150200 250 300 350
Shear rate, (s
- 1
)
Shear stress (Pa)
20.0 vol.%
26.7.0 vol.%
30.8 vol.%
35.4 vol.%
37.8 vol.%
40.4 vol.%
43.7 vol.%
46.0 vol.%
It can be seen that slurries up to 37.8 vol. % show Newtonian behavior while beyond this vol. %,
the slurry shows pseudoplastic nature. Therefore, it can be inferred that slurry changes to non-
Newtonian behavior beyond 37.8 vol. %. The power law flow parameters
n
and K values for
slurry samples S-1 and S-2 at 40.4, 43% and 46.0 vol. % were given in Table 2 indicating the
pseudoplastic nature of the limestone slurry at these concentrations. The power law model fitted
the experimental data excellently at higher solids concentration and is given by:
n
K γτ = (4)
Where
τ
is the shear stress,
γ
is the shear rate,
K
is the consistency parameter
n
is the flow
behavior index.
Table 2. Power law flow parameters for limestone slurry samples S-1 and S-2 at higher solids
concentrations (C
v
, %).
C
v
, % S-1 S-2
n K n K
40.4 0.55 0.16 0.57 0.10
43.0 0.57 0.54 0.58 0.396
46.0 0.616 0.90 0.64 0.58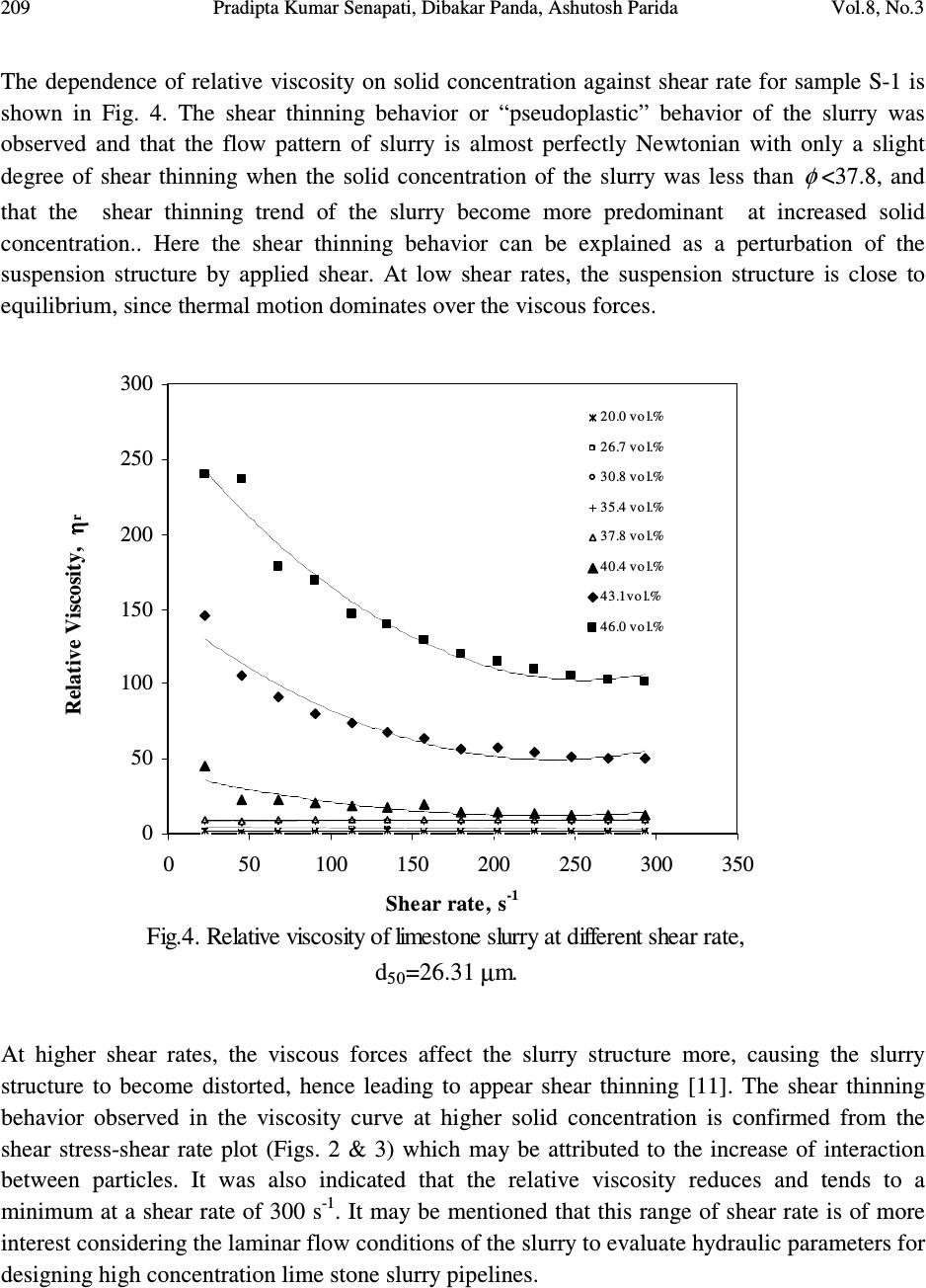

209 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
The dependence of relative viscosity on solid concentration against shear rate for sample S-1 is
shown in Fig. 4. The shear thinning behavior or “pseudoplastic” behavior of the slurry was
observed and that the flow pattern of slurry is almost perfectly Newtonian with only a slight
degree of shear thinning when the solid concentration of the slurry was less than
φ
<37.8, and
that the shear thinning trend of the slurry become more predominant at increased solid
concentration.. Here the shear thinning behavior can be explained as a perturbation of the
suspension structure by applied shear. At low shear rates, the suspension structure is close to
equilibrium, since thermal motion dominates over the viscous forces.
Fig.4. Relative viscosity of limestone slurry at different shear rate,
d
50
=26.31 µm.
0
50
100
150
200
250
300
050100150200 250300350
Shear rate, s-1
Relative Viscosity, η
η η
ηr
20.0 vol.%
26.7 vol.%
30.8 vol.%
35.4 vol.%
37.8 vol.%
40.4 vol.%
43.1 vol.%
46.0 vol.%
At higher shear rates, the viscous forces affect the slurry structure more, causing the slurry
structure to become distorted, hence leading to appear shear thinning [11]. The shear thinning
behavior observed in the viscosity curve at higher solid concentration is confirmed from the
shear stress-shear rate plot (Figs. 2 & 3) which may be attributed to the increase of interaction
between particles. It was also indicated that the relative viscosity reduces and tends to a
minimum at a shear rate of 300 s
-1
. It may be mentioned that this range of shear rate is of more
interest considering the laminar flow conditions of the slurry to evaluate hydraulic parameters for
designing high concentration lime stone slurry pipelines.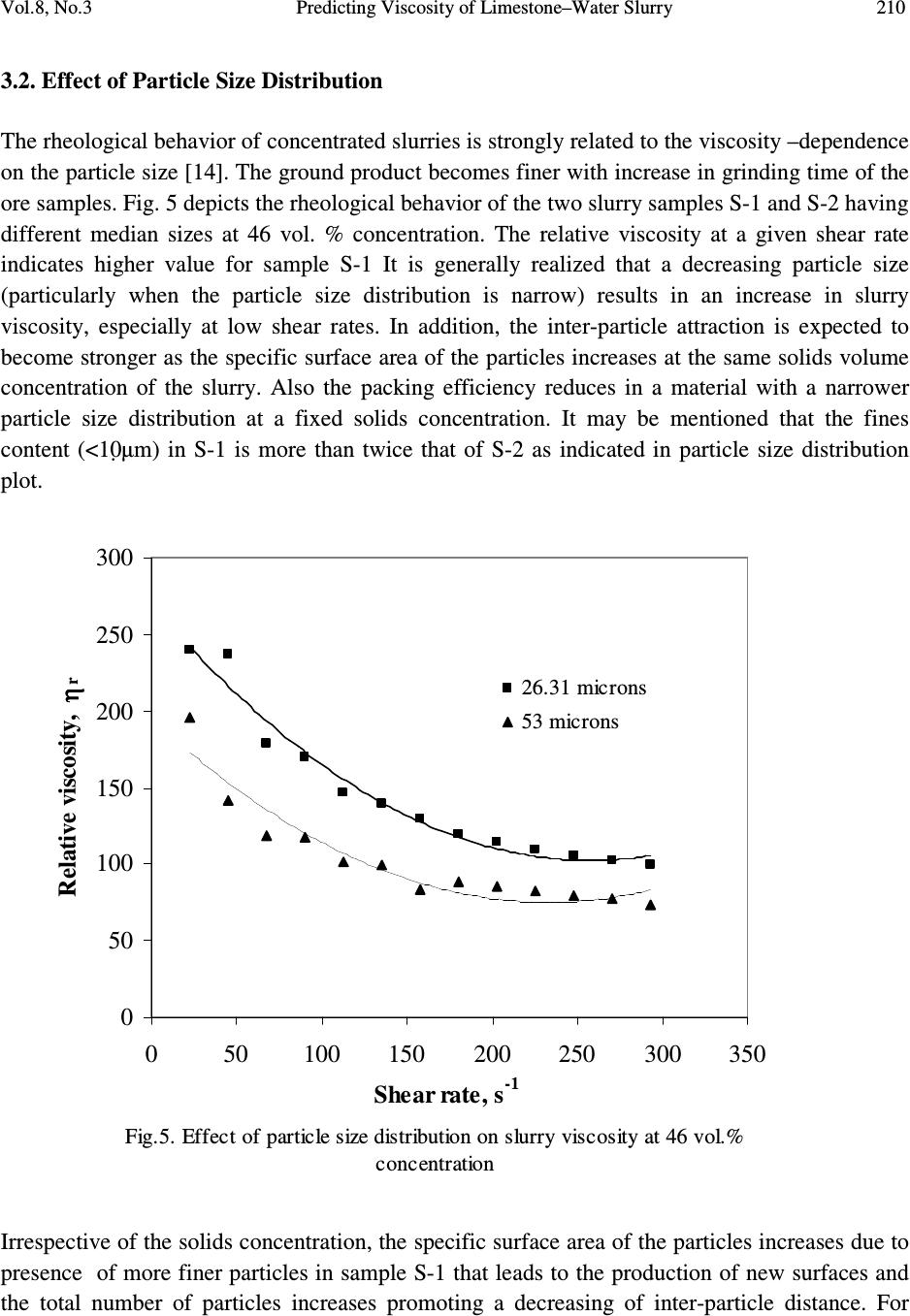

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 210
3.2. Effect of Particle Size Distribution
The rheological behavior of concentrated slurries is strongly related to the viscosity –dependence
on the particle size [14]. The ground product becomes finer with increase in grinding time of the
ore samples. Fig. 5 depicts the rheological behavior of the two slurry samples S-1 and S-2 having
different median sizes at 46 vol. % concentration. The relative viscosity at a given shear rate
indicates higher value for sample S-1 It is generally realized that a decreasing particle size
(particularly when the particle size distribution is narrow) results in an increase in slurry
viscosity, especially at low shear rates. In addition, the inter-particle attraction is expected to
become stronger as the specific surface area of the particles increases at the same solids volume
concentration of the slurry. Also the packing efficiency reduces in a material with a narrower
particle size distribution at a fixed solids concentration. It may be mentioned that the fines
content (<10  µ m) in S-1 is more than twice that of S-2 as indicated in particle size distribution
plot.
Fig.5. Effect of particle size distribution on slurry viscosity at 46 vol.%
concentration
0
50
100
150
200
250
300
050100 150200 250300 350
Shear rate, s
-1
Relative viscosity, η
η η
η
r
26.31 microns
53 microns
Irrespective of the solids concentration, the specific surface area of the particles increases due to
presence of more finer particles in sample S-1 that leads to the production of new surfaces and
the total number of particles increases promoting a decreasing of inter-particle distance. For

211 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
sample S-2 with larger median particle size and with less proportion of finer particles, the
interaction between particles is weak. Hence the relative viscosity indicates higher values for S-1
than S-2 at a specific solids concentration and shear rate. Also the power law model involving n
and K depicts the rheological behavior of both the limestone slurry samples at higher solids
concentration (>37.8 vol.%). The decreasing trend of n and increasing trend of K at the specified
solids concentrations is well marked when the median particle size decreases as shown in Table
2.
3.3. Effect of Slurry Temperature
During the process of grinding the ore samples, the temperature of ground slurry fluctuates
between 30
O
to 60
O
C depending upon the grinding conditions which affects the slurry rheology
[15]. Therefore the temperature dependence of viscosity of lime stone slurry was also
investigated in the shear rate range of 1 to 300 s
-1
. Figure 6 shows the variation of temperature
with relative viscosity of the limestone slurry sample S-1 at 40.4 vol.%, 43.1 vol.% and 46.0
vol.% solids concentration respectively. The relative viscosity of the slurry decreases in the
range of temperature studied (30
O
C – 50
O
C). The trend of decreasing viscosity at elevated
temperatures occurs due to increased kinetic energy of the particles promoting the breakage of
intermolecular bond between adjacent layers which results in decrease in viscosity of the
limestone slurry.
Fig.6.Effect of temeprature on relative viscosity of limestone slurry at
different solids concentrations, d
5 0
=26.31 µm
0
20
40
60
80
100
120
25 30 3540 45 50 55
Temperature.
O
C
Relative viscosity, η
η η
η
r
40.4 vol.%
43.1 vol.%
46.0 vol.%

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 212
Also the temperature dependence of viscosity can be represented in terms of a simple Arrhenius
type of equation for the range of temperature investigated. The relation between viscosity and
temperature may be presented as
RT
E
r
a
Ae= η
(5)
or
A
RT
E
r
a
lnln += η
(6)
where,
r
η is the relative viscosity at a particular shear rate,
a
E is the fluid –flow activation
energy,
T
is the temperature in Kelvin, R is the universal gas constant, and A is a fitting
parameter. A plot of relative viscosity versus reciprocal of absolute temperature should be linear
which is quite evident from Figure 7 for the lime stone slurry.
Fig.7. Effect of slurry temperature with relatve viscosity, d
50
=26.31 µ
m
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0.003050.0031 0.003150.00320.003250.0033 0.00335
1/T
O
K
Ln η
η η η
r
35.40%
37.80%
40.40%
4 3.10%
46%
3.4. Viscosity Model Fitting
The maximum solid fraction)(
m
φ can be determined either by using the experimental data from
rheological measurements or by utilizing theoretical approach. By adopting experimental
approach, the relative viscosity at various volume fractions of solids are measured and plotted
and the corresponding value of
φ
at high volume fractions of solids where a sharp increase in

213 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
viscosity is observed may be considered as
m
φ [5]. For the limestone-water slurry sample S-1, it
was found that the relative viscosity sharply increases at a solids fraction of
m
φ ~0.462 (Fig. 8).
Fig.8. Experimental measurement of maximum solid fraction (Φ
m
) in
studied range of limestone slurry.
0
20
40
60
80
100
120
00.05 0.1 0.15 0.2 0.250.3 0.35 0.4 0.45 0.5
Solid fraction (vol.%)
Relative Viscosity, η
η η
η
r
The relative viscosity of the limestone-water slurry, under given solids fractions were predicted
by applying the various theoretical and empirical models. Five models namely Liu’s model,
Dabak et al. model [16], Krieger-Dougherty equation 17], Mooney’s equation [18], Chong et al.
model [19] were utilized to predict the slurry viscosity and the models are presented in Table 3.
Liu [9] has proposed a model to estimate the theoretical, maximum solid fractions (
m
φ )
allowable for given suspension at which the slurry viscosity approaches infinity. The equation
involves a linear relationship of
21
1
−
−
r
η with
φ
which predicts the maximum solid fractions
(
m
φ ) and is given as:
ba
n
r
+=−
−
φη
1
1 (7)
Where, the constant
a
(slope of the straight line) and b (intercept value) were determined from
the )1(
1 n
r
−
− η -
φ
relationship using the experimental data.

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 214
Table 3. Different Models utilized to predict relative viscosity (
r
η ) of the Limestone slurry.
Models
Equation
Liu’s model
n
mr
a
−
−= )]([ φφη
Dabak et al.
mode
n
m
m
r
n





−
+= )(
][
1
φφ
φφη
η
Krieger
-
Dougherty
equation
m
m
r
φη
φ
φ
η
][
1
−














−=
Mooney’s
equation








−
=
φ
φη
η
K
r
1
][
exp
Chong et al.
model
2
)(1
)(75.0
1





−
+=
m
m
r
φφ
φφ
η
As shown in Fig. 9, the maximum solids fraction (
m
φ ) was determined to be 0.504 by
extrapolating the fitted line to
21
1
−
−
r
η =1. The intersection point of the dashed line at Y=1 and
the extrapolated fitted line gives the value of
m
φ .
This value was low when it is compared with what is achievable by the random close packing of
mono-size spheres (
m
φ =0.64). It is presumably due to the apparent particle agglomerations found
in the starting limestone powder samples that exist persistently in the suspension to an
unspecified extent even after high –shear ball milling.
For high solids concentration, the viscosity model for slurry as proposed by Liu is given as:
2
)]([
−
−= φφη
mr
a (8)
The term )( φφ −
m
is the effective space available for the particles to move in the matrix media.
The effective space reduces as
m
φφ => , and the viscosity of mixture slurry becomes thicker and
finally becomes infinite at the point of
m
φ . The above Eq. (8) is valid for highly concentrated
slurries under sufficient shear conditions. However, taking into account a variety of materials

215 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
and shearing conditions the generalized form of the Eq. (8) is given in Table 3, where ‘
n
’ is a
flow–dependant parameter and suspension specific. For the present investigation the values
a
and
n
determined from Liu’s analytical model is given in Table 4. These values were adopted
to calculate the viscosity of limestone-water slurry and the data fitted reasonably better in the
range of solids concentration studied.
Fig. 9. Typical 1-η
r
- 0. 5
- Φ relationship for limestone slurry.
y = 2.3561x - 0.188
R
2
= 0.9767
0
0.2
0.4
0.6
0.8
1
1.2
0.1 0.2 0.30.4 0.5 0.6
Solid Fraction (Φ
ΦΦ
Φ)
1-η
η η
η
r
- 0.5
The second model developed by of Dabak et al. involves two adjustable parameters [
η
] and a
term ‘
n
’ which is applicable over both low and high shear regions. Taking the value of ‘
n
’as
n
=2, the linearized form of the model equation can be expressed in the form of:
)(2
][
1
21
φφ
φφη
η
−
=−
m
m
r
(9)
and the intrinsic viscosity [
η
] was determined using 1
5.0
−
r
η versus )/( φφφ −
m
plot and is given
in Table 4.

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 216
Table 4. Model parameter values utilized to compute Relative viscosity of limestone slurry.
Various Models Model Parameter values
Liu’s model
m
φ = 0.504
a
= 2.3561
n
= 2
Dabak et al. model
m
φ = 0.504
n
= 2
[
η
] = 3.422
Krieger-Dougherty
equation
m
φ = 0.504
[
η
] = 3.581
Mooney’s equation
m
φ = 0.504
[
η
] = 3.581
K
=1.4
Chong et al. model
m
φ = 0.504
n
= 2
The third model invoked to compare the experimentally determined viscosity values was
Krieger-Dougherty equation which gives a reasonable approximation of the rheological data for
uniform-sized colloidal suspension with spherical geometry of the particles. The linearized form
of the semi empirical model can be written as:
)1ln(][)ln(
m
mr
φ
φ
φηη −−= (10)
Where [
η
] is the intrinsic viscosity.
The value of intrinsic viscosity ][
η
was obtained from a linear fit of ln(
r
η ) – ln)1(
m
φ
φ
− with the
intercept through the origin and is given in Table 4. The intrinsic viscosity value obtained is
close to the value computed by using Eq. 9. However the value of ][
η
so obtained deviates
substantially from [
η
] =2.5 for the mono-sized spherical particles in suspension, presumably due
in part to the agglomerated nature of the particles used, as well as to the particle size distribution
involved in the starting powder.

217 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
The fourth model used was Mooney’s equation for predicting the relative viscosity (
r
η ), which
does not involve the maximum solids fraction
m
φ . An adjustable parameter
K
in the equation
was determined by taking the computed value of intrinsic viscosity [
η
] from other models and is
given in Table 4.
The last empirical model proposed by Chong et al. for highly concentrated poly-dispersed
suspension was used to predict the viscosity of the slurry, where
m
φ is the maximum solids
fraction of a given powder. The value of
m
φ =0.504 computed from Liu’s theoretical model was
used to predict the viscosity of limestone slurry at different solids concentration.
3.4.1 Comparison of models
The comparison of predictive
r
η and the experimentally measured
r
η at solids concentration
studied in the present investigation are presented in Table 5.
Table 5. Prediction of relative viscosity (
r
η ) using different models.
C
v
, %
Experim ental
r
η
Liu’s
Model
Dabak et
al. Model
Krieger
-
Dougherty
Model
Mooney’s
Equation
Cho
ng et
al. Model
20.0 1.822 1.95 2.46 2.5 2.70 2.23
26.7 3.422 3.21 3.88 3.9 4.60 3.4
30.8 5.57 4.7 5.54 5.49 6.95 4.74
35.4 8.66 8.01 9.21 8.91 12.34 7.67
37.8 9.011 11.35 12.86 12.2 17.72 10.56
40.4 12.453 18.01 20.10 18.52 27.95 16.24
43.1 49.97 33.80 37.10 32.69 48.98 29.46
46.0 100.92 93.05 100.31 81.52 102.22 78.16
For the given limestone slurry system it was indicated from Table 5 that all the models gave a
reasonable estimation of the relative viscosity (
r
η ) over a solids concentration range C
v
=20.0-
37.8 vol. %. The models of Liu, Krieger-Dougherty and Chong et al. better predicted the relative
viscosity values at solids concentration of 40.4 vol. % whereas the models proposed by Mooney
Liu and and Dabak et al agreed quite well beyond solids concentration of 40.4 vol. %. However,
Liu model favourbaly fitted the experimental data at low as well as high solids concentration.

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 218
The calculated %, errors as shown in Table 6 and the discrepancy in predicting
r
η (over and
under prediction of the models with experimentally measured data) by using different models
may be attributed to various factors as enumerated in the following paragraph.
Table 6. The calculated %, errors in predicting the relative viscosity (
r
η ) with different models.
Liu’s Model Dabak et al.
Model
Krieger-
Dougherty Model
Mooney’s
Equation
Chong et al.
Model
-7.02 -35.01 -37.21 -48.18 -22.4
6.2 -13.38 -13.96 -34.42 0.64
15.62 0.54 1.43 -24.77 14.9
7.5 -6.35 -2.88 -42.49 11.43
-25.95 -42.71 -35.39 -96.65 -17.19
-44.62 -61.4 -48.72 -124.44 -30.41
32.36 25.75 34.58 1.98 41.04
7.8 0.604 19.22 -1.28 22.55
*Negative sign indicates over prediction
**Positive sign indicates under prediction
The shear thinning behavior of the limestone slurry in the range of shear rate studied is typical of
agglomerated or flocculated suspensions. The presence of flocculants may increase the viscosity
of the slurry at higher solids concentration which requires application of more amount of stress
to promote particle alignment in the direction of shear by breaking down the structure of
floc/aggregates. This indicates that in a lower range of shear rates, the attractive interparticle
force is predominant over the hydrodynamic force exerted by a flow field affecting slurry
viscosity [12]. Also the repulsive forces due electrostatic interactions are quite significant in
aqueous suspensions. The other factors such as particle shape effect of the limestone powder,
particle size and size distribution, distribution of the carrier medium i.e. water in the suspension
may contribute to the discrepancy observed with various models [7, 20]. In addition, the models
used all assume implicitly a ‘hard’ and same diameter sphere model in given suspension system.
Therefore, the discrepancy was found in the rheological prediction among all models.
4. CONCLUSIONS
The rheologcal behavior of limestone slurry of Purnapani limestone mines in aqueous medium
were investigated which indicated pseudo plastic shear thinning behavior beyond 37.8 vol.%.
The maximum solids fraction (
m
φ ) of the slurry was theoretically determined using Liu’s model
and the value of
m
φ was found to be 0.504 for the given slurry system. Five models namely
Liu’s model, Dabak et al. model, Krieger-Dougherty equation, Mooney’s equation, Chong et al.

219 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
model were utilized to predict and compare the slurry rheology. The Liu’s model fitted
reasonably better the experimental data at all range of solids concentration investigated. The
influence of particle size distribution also significantly affects the slurry rheology which was
quite evident for the two limestone samples S-1 and S-2 with different d
50
(median particle size)
and extent of fines content. The sample S-1 with d
50
= 26.31 µm and more percentage of fines
content (< 10  µm) exhibited higher relative viscosity than S-2 at a specified solids concentration
of the slurry within the studied range of shear rates. Also the relative viscosity of the slurry
reduces with increase in temperature and the change in relative viscosity with temperature of
limestone slurry could be described by a simple Arrhenius type of equation for the range of
temperature and concentration investigated
The two parameter equation involving ‘
a
’ and
m
φ proposed by Liu may enable accurate
prediction of slurry rheology with respect to solids concentration for maintaining the desired
slurry viscosity. This will be beneficial in evaluating the hydraulic parameters accurately from
slurry rheology such as optimum solids concentration, design velocity, pumping power
requirement, and specific power consumption etc. for commercial design of limestone slurry
pipelines at higher solids concentration.
ACKNOWLEDGEMENT
The authors are gratefully indebted to Prof. B.K.Mishra, Director, IMMT, Bhuabneswar, India
for giving permission to publish the paper and Steel Authority of India Limited (SAIL),
Rourkela, Orissa for supporting the investigations.
Nomenclature
A fitting parameter in Arrhenius equation.
C
v
solids concentration, vol. %
a
E fluid-flow Activation Energy, kJ mol
-1
K
crowding factor in Mooney’s Equation
K
consistency parameter
M
mass of solids/liquid, kg
R universal gas constant, 8.3144 kJ/kg mole K
T
temperature in Kelvin
V volume of solids/liquid, m
3
a
slope of the straight line in equation 5. (Liu’s model)
b intercept value in equation 5. (Liu’s model)
d
50
median particle size
l subscript for liquid
n
flow–dependant parameter and suspension specific in equation 7.
s
subscript for solids

Vol.8, No.3 Predicting Viscosity of Limestone–Water Slurry 220
φ
volume fraction of solids (solids fraction)
m
φ maximum solids fraction (maximum particle packing density)
r
η relative viscosity
[
η
] Intrinsic viscosity, Pas
ρ
density of solids/liquid, kg/m
3
n
flow behavior index.
τ
shear stress, Pa
γ
shear rate, S
-1
REFERENCES
[1] Govier, G.W, Aziz, K., (1972). “ The Flow of Complex Mixtures in Pipes” , Van Nostrand
Reinhold Company: New York.
[2] Muster, T.H. & Prestidge, C.A., (1995), “Rheological investigations of sulphide mineral
slurries”, Minerals Engineering , vol.8, pp.1541-1555.
[3] Weltmann, R.N. & Green, H., (1943), “Rheological Properties of Colloidal Solution,
Pigment Suspensions and Oil mixtures”, Journal of Applied Physics , vol.14, pp.569-576.
[4] Goodwin, J.W., (1975), “The Rheology of Dispersions”, Colloid Science , vol. 7, pp.
246-293.
[5] Firouzi, J., Akbar Yousefi, A. & Langroudi, A.E., (2006), “Rheological Behaviour of
Metal powder Suspensions under Dynamic loading” , Iranian Polymer Journal , vol.
15(2), pp. 127-134.
[6] Garcia, F., Bolay, N. le. & Frances, C., (2003), “Rheological behaviour and related
granulometric properties of dense aggregated suspensions during an ultrafine
comminution process”, Powder Technology.130, 407-414.
[7] Liu, D.M., (1999), “Control of yield stress in low-pressure ceramic moldings”, Ceramic
International , vol. 25, pp. 587-592.
[8] Liu, D.M. & Tseng, W.J., (2000), “Rheology of injection-molded zirconia–wax
mixtures”, Journal of Material Science , vol. 35, pp. 1009-1016.
[9] Liu, D.M., (2000), “Particle packing and rheological property of highly-concentrated
ceramic suspensions:
m
φ determination and viscosity prediction”, Journal of Materials
Science , vol. 35 , pp. 5503-5507
[10] Tseng, W.J. & Yu Li, S., (2002), “Rheology of Colloidal BaTiO
3
suspension with
ammonium polyacrylate as a dispersant”, Journal of Materials Science and Engineering .
A vol. 333, pp. 314-319.
[`11] Yuanling, S., Xiaolin, L. & Jianfeng, C., (2004), “The maximum solid loading and
viscosity estimation of ultra-fine BaTiO
3
aqueous suspensions”, Colloids and surfaces A:
Physicochemical Engineering Aspects, vol. 247, pp. 27-34.

221 Pradipta Kumar Senapati, Dibakar Panda, Ashutosh Parida Vol.8, No.3
[12] He, M., Wang, Y. & Forssberg, E., (2004), “Slurry rheology in wet ultra-fine grinding of
industrial minerals: a review”, Powder Technology . Vol. 147, pp. 267-304.
[13] He, M., Wang, Y. & Forssberg, E., (2006, “Parameter studies on the rheology of
Slurries”, International Journal of Mineral Processing , vol. 78, pp. 63-77
[14] Tangsathitkulchai, C., Austin, L.G., (1988), “Rheology of concentrated slurries of of
natural size distribution produced by grinding”, Powder Technology, vol. 56, pp. 293-
299.
[15] Gao. M., Forsberg. E., (1993), “The influence of slurry rheology on the ultra-fine
grinding in a stirred ball mill”, Proceedings of XVIII International Mineral Processing
Congress, Sydney, Australia, vol.2. pp. 237-244.
[16] Dabak, T. & Yucel, O., (1986), “Shear Viscosity behaviour of highly
concentrated suspensions at low and high shear rates”, Rheologica Acta, vol. 25,
pp. 527 533
[17] Krieger, I.M & Dougherty, T.J., (1959), “A Mechanism for non-Newtonian flow in
suspensions of rigid spheres”, Trans. Soc. Rheol . Vol. 3, pp. 137-148.
[18] Mooney, M., (1951), “The viscosity of concentrated suspension of spherical particles”,
Journal of Colloid Science , vol. 6, pp. 162-170.
[19] Chong, J.S., Christiansen, E.B. & Baer, A.D., (1971), “Rheology of concentrated
Suspensions”, Journal of Applied Polymer Science , vol. 15, pp. 2007-2021.
[20] Bergstrom, L., (1994), “Surface and Colloid Chemistry in Advanced Ceramic
Processing”, Marcel Dekker: New York