Journal of Min erals & Materials Characterization & Engineering , Vol. 8, No.1, pp 73-78, 2009
jmmce.org Printed in the USA. All rights reserved
73
In-Vitro Studies of Artificially Removed Human Renal Stone Minerals
by Sonic Engineering Approach-I
G. Kanchana, P. Sundaramoorthi*, and G.P. Jeyanthi
Department of Bio-chemistry, Avinashilingam University for Women, Coimbatore, India.
*Department of Physics, Thiruvalluvar Govt. Arts College, Rasipuram, Namakkal,
India-637401.
(Ph.No.-04287-231802 (off.) Fax- 04287-231882 , MailID-moorthi.sundara@gmail,com)
ABSTRACT
Ultrasonic waves are the main tools for measuring the unknown parameters in
science and technological analysis of a particular biological sample. The sonic wave velocity
measurement applied in the in-vitro & in-vivo studies in medical fields has been made in
different renal stones removed from the human kidney. The samples were analyzed at different
frequencies and the corresponding wavelength at room temperature (305K) were found. The
experimental results have been used to calculate many physical constants of the samples, such
as stone density, sonic velocity, acoustical wavelength, specific acoustic impedance,
transmitivity, reflectivity and dynamic modulus of elasticity. The investigated results have
been agreed to the reported information.
Key Words: Mineral processing, Sampling, Process instrumentation, Bio-oxidation, Ion
exchange
1. INTRODUCTION
The ultrasonic sound velocity gives the necessary data in all the states. From the
sonic velocity of a particular medium and its propagation results, one can find the texture,
structure, porosity, compression, and particle size in a direction, which is kept at constant
physical and chemical environments. More number of parameters can be calculated in solids
[1-2] and hence it is applied to the human physiological disorders. Ultrasonic wave velocity
has been used in conventional medical diagnostics therapy and surgical tools in different
sensitive parts of the human body such as brain, glands, breast, heart, urinary tracts,
peripheral blood vessels, reproductive organs, etc.[3-5]. Especially in a human physiological

74 G. Kanchana, P. Sundaramoorthi*, and G.P. Jeyanthi Vol.8, No.1
system, kidney is a major organ, which separate extra minerals, water, wastes etc. from the
blood after digestion. In the pathological condition let the kidney failure, inhibitor disorder,
and increase in mineral values in the blood or urine continuously, one can get the renal
stones any where within the urinary tracts. The kidney stone formation, or renal stone
diseases or mineral deposition or crystals grown in the kidney creates socio-economic
disorders. To avoid this type of problem one must clearly know about the diseases to prevent
the deposition either before the start or after the start. Extra corporeal shock wave lithotripsy
(ESWL), Laser and UV has created large disadvantages such as tissue damage, pain etc. [6-
8] which can be overcome by ultrasonic method of treatment [9]. In the present
investigation, the longitudinal sonic parameters of six different kidney stones at different
frequency ranges from 0.5MHZ to 12 MHZ at 305K were used.
2. MATERIALS AND METHODS
Many methods are used to measure the ultrasonic parameters in the biological
system. In the present investigation, pulse echo overlap (PEO) technique was used with the
good accuracy. The PEO method is applied in diagnostic purpose as well as the tissue
characterization in a static and dynamic system. A double probe contact (between the kidney
stones) through transmission technique was used for the measurement of this parameter. The
transmitter, receiver transducers are controlled by the computer. Similar studies have already
been carried out in gallstones [10]. From the observation, it gives directly the parameters of
pulse transit time (t) for the known thickness (d). Using the available data the acoustical
impedance (Z), density (p) of the samples, pressure amplitude coefficient (R), pressure
amplitude transmission coefficient (T) and dynamic modulus of elasticity (E) of all the
samples were calculated.
In the present studies different types of stones were collected in and around
Namakkal District local hospitals in Tamil Nadu. India. The stones were named as A, B, C,
D and E. The stones were removed from the kidney by applying the ultrasonic lithotripsy
process. The samples were collected, cleaned and then preserved. The chemical
compositions of all the samples were by bio-chemical methods. The constituents of the
samples are tabulated in Table-1. In this study, it is assumed that in-vitro calculation gives
good representation of the natural properties of the biological stones and characteristics of
the vivo solution.
3. RESULTS AND DISCUSSIONS
The artificially removed renal stone samples were photographed using digital camera
and find its dimensions. The renal stone samples are shown in Fig.1-5. Samples were
analyzed by bio-chemical methods to identify the chemical constituent present in the
samples. The corresponding samples composition and its various types of stones are shown
in Table-1. The various parameters of the stones, such as mass, size, volume and density are
presented in Table-2. It is clear that the B sample has more density and less volume than the
sample D. The frequencies and wavelength of the corresponding samples at particular

Vol.8, No.1 In-Vitro Studies of Artificially Removed Human Renal Stone 75
velocity of the ultrasonic samples at constant temperature were recorded in Table-3. From
the data, the frequency and wavelength is inversely proportional to each other. The specific
acoustic impedance of all the samples were calculated and recorded in Table-4. With
reference to the density of air medium, and ultrasonic velocity then acoustical impedance of
the medium, the reflectivity, transmitivity were calculated and recorded in Table-5. The
dynamic elasticity of the renal stones at room temperature (305K) were calculated and
recorded in Table-6. Densities of the samples are directly proportional to the dynamic
modulus of elasticity [11].
Fig.1-5 Renal stones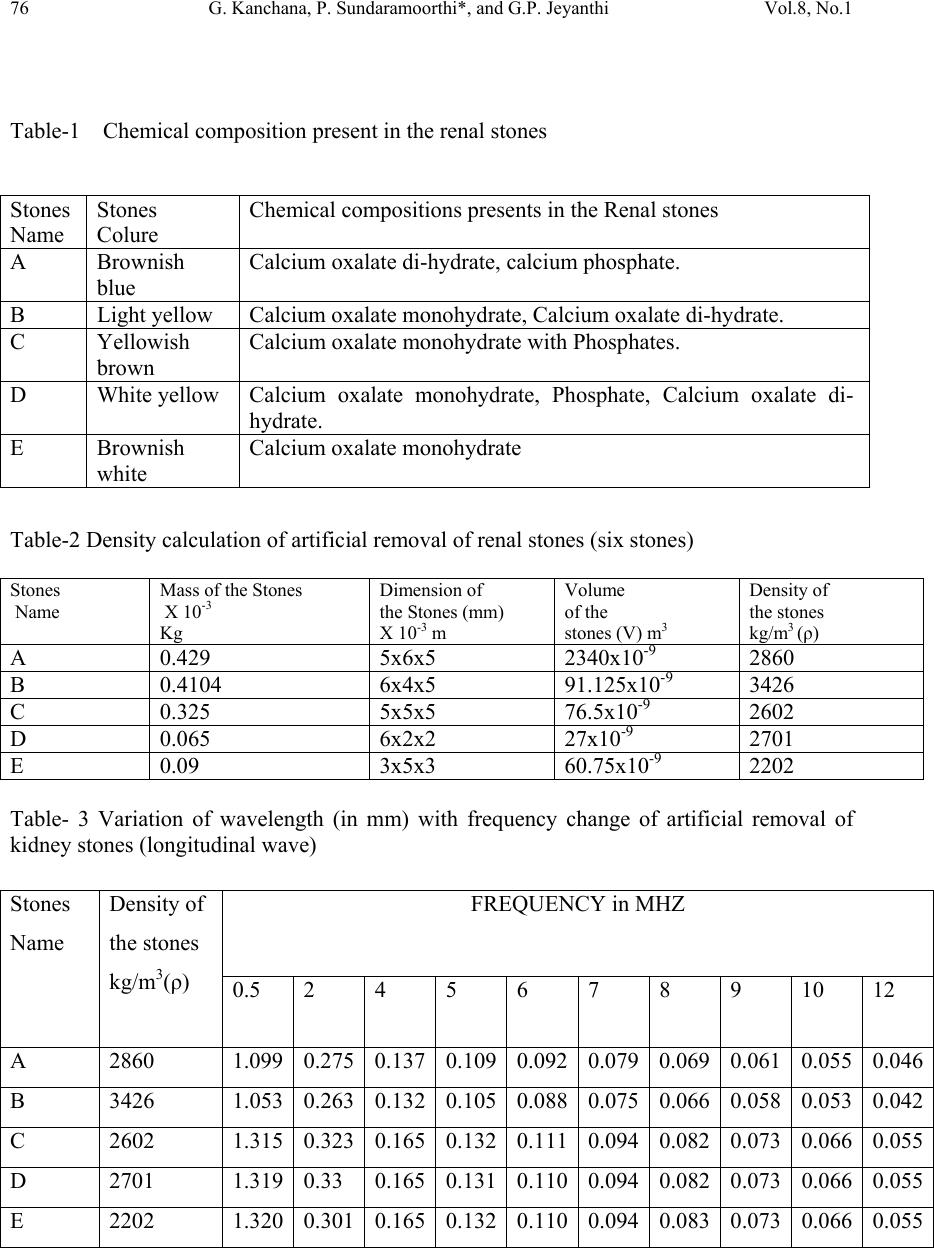

76 G. Kanchana, P. Sundaramoorthi*, and G.P. Jeyanthi Vol.8, No.1
Table-1 Chemical composition present in the renal stones
Stones
Name
Stones
Colure
Chemical compositions presents in the Renal stones
A Brownish
blue
Calcium oxalate di-hydrate, calcium phosphate.
B Light yellow Calcium oxalate monohydrate, Calcium oxalate di-hydrate.
C Yellowish
brown
Calcium oxalate monohydrate with Phosphates.
D White yellow Calcium oxalate monohydrate, Phosphate, Calcium oxalate di-
hydrate.
E Brownish
white
Calcium oxalate monohydrate
Table-2 Density calculation of artificial removal of renal stones (six stones)
Stones
Name
Mass of the Stones
X 10-3
Kg
Dimension of
the Stones (mm)
X 10-3 m
Volume
of the
stones (V) m3
Density of
the stones
kg/m3 (ρ)
A 0.429 5x6x5 2340x10-9 2860
B 0.4104 6x4x5 91.125x10-9 3426
C 0.325 5x5x5 76.5x10-9 2602
D 0.065 6x2x2 27x10-9 2701
E 0.09 3x5x3 60.75x10-9 2202
Table- 3 Variation of wavelength (in mm) with frequency change of artificial removal of
kidney stones (longitudinal wave)
Stones
Name
Density of
the stones
kg/m3(ρ)
FREQUENCY in MHZ
0.5 2 4 5 6 7 8 9 10 12
A 2860 1.099 0.2750.1370.1090.0920.0790.069 0.061 0.0550.046
B 3426 1.053 0.263 0.132 0.105 0.088 0.075 0.066 0.058 0.053 0.042
C 2602 1.315 0.323 0.165 0.132 0.111 0.094 0.082 0.073 0.066 0.055
D 2701 1.319 0.33 0.165 0.131 0.110 0.094 0.082 0.073 0.066 0.055
E 2202 1.320 0.301 0.165 0.132 0.110 0.094 0.083 0.073 0.066 0.055

Vol.8, No.1 In-Vitro Studies of Artificially Removed Human Renal Stone 77
Table- 4 Specific acoustic impedance of the renal stones
Stones
Name
.
Volume of
the stones
(V) 10-9 m3
Density of
the stones(ρ)
Kg/m3
Velocity of the
Ultrasonic wave
m/sec
Specific acoustic
Impedance (Z)
Z=(ρ x c) X106
ohms
A 150 2860 549.9 1.9994
B 120 3426 526 1.9995
C 125 2602 657.9 1.9995
D 24 2701 659.3 1.9995
E 45 2202 660.1 1.9994
Table-5 Reflection co-efficient and transmission co-efficient of the renal stones
Density of air=1.26 Kg/m3.
Acoustic impedance of air (Z1) = 425.7.
Velocity of ultrasonic in air =330 m/sec
Stones
Name.
Volume of
the stones
(V) 10-9
m3
Density o
f
the
stones(ρ)
Kg/m3
Velocity of
the
Ultrasonic
wave m/sec
Specific
acoustic
Impedance
Z=(ρxc)
X106
ohms
Reflectivity
( R )
Transmitivity
( T )
A 150 2860 549.9 1.9994 0.9995 1.9994
B 120 3426 526 1.9995 0.9995 1.9995
C 125 2602 657.9 1.9995 0.9995 1.9995
D 24 2701 659.3 1.9995 0.9995 1.9995
E 45 2202 660.1 1.9994 0.9994 1.9994

78 G. Kanchana, P. Sundaramoorthi*, and G.P. Jeyanthi Vol.8, No.1
Table-6 Dynamic modulus of elasticity of the renal stones (E)
Stones
Name
Volume of
the stones
(V) 10-9 m3
Density of
the stones(ρ)
Kg/m3
Velocity of
the
Ultrasonic
wave
m/sec
Specific
acoustic
Impedance (Z)
Z=ρ x c X106
Ohms
Dynamic
modulus of
elasticity of
stones
(E) x 1010
Nm-2
A 150 2860 549.9 1.9994 0.4496
B 120 3426 526 1.9995 0.6174
C 125 2602 657.9 1.9995 0.4455
D 24 2701 659.3 1.9995 0.4810
E 45 2202 660.1 1.9994 0.3202
4. CONCLUSIONS
From these investigations, one can understand the chemical constituents present in the
samples, the ultrasonic velocity, specific acoustic impedance, reflectivity, transmitivity and
dynamic modulus of elasticity of all the samples. All the observed data in this study are in
close agreement with the results of earlier workers in gallstones. The results give the
necessary information about the ultrasonic propagation in different types of renal stones. The
in-vitro information helps the identification and understanding of the future in-vivo studies.
REFERENCES
[1] S. Balakrishana. Ind. Minerals, 1, 57, (1960).
[2] M. Auberger and S.J. Rirhart., J. Acc. Soc. Am.32 1698, (1968).
[3] P.N. Well. , Bio. Ultra. (Academic Press London), (1977).
[4] G. Heap., Br J. Urol. 40 485 (1968).
[5] F.G.M. Ross., Ultra.cli. diag. (John Willy, London) p 143.
[6] V.R. Singh., R.Agarwal., Ind. J. Pure & Appl. Phys., 6, 475 (1968).
[7] E.R. Sosa., SPAN, 2 , 44, (1988).
[8] A.J. Coleman, J.E.Saunders, Ultra., 75 (1993).
[9] N. Krishanamoorthi, S. Balakrishanan. Geo. Phys 22, 268, (1968).
[10] Jasure Singh, et al., Ind. J. Pure & Appl. Phys. 35, 452-455, (1997).
[11] P. Sundaramoorthi and S. Kalainathan, J. Curr. Sci. 9 (2) 569, (2006).