Journal of Minerals & Materials Characterization & Engineering, Vol. 7, No.1, pp 71-82, 2007
jmmce.org Printed in the USA. All rights reserved
71
Development of Mathematical Equation for Fraction of Solid in
AlSi7Mg Alloy Solidification Simulation
O.O. Oluwole*, G.O. Oluwadare , A.A. Afonja
Materials Science and Engineering Department,
Obafemi Awolowo University, Ife, Nigeria.
* Correspondence author: e-mail [e-mail], Phone:[phone]
ABSTRACT
Thermodynamic data is made use of in calculating fraction of metal solidified in
solidifcation simulation. However, thermodynamic data for many industrial alloys in
their solidification ranges are not available for most practicing engineers. It is thus
desirable to develop reliable equations that can be used in calculating fraction of metal
solidified for solidification simulation. This work has developed an equation to calculate
fraction of metal solidified for AlSi7Mg alloy solidifying under fast cooling conditions
using generated values from thermodynamic data.
Keywords: Solidification simulation, mathematical equation, fraction of solid, AlSi7Mg
1. INTRODUCTION
Numerical simulation is a very useful tool in predicting the final state of cast parts.
The purpose of simulating solidification in castings is to identify designs that are likely to
cause defects due to the temperature variations in the solidifying metal. Also
microstructure simulation is being done to ascertain the microstructures formation before
casting. If successive time- solidification temperatures profiles show hotspots which will
induce solidification defects such as shrinkage porosities, pipe and hot tears, the design
variables could be modified or the decisions to use solidification aids such as chills and
paddings could be made [1]. Thus, the ability to model a variety of casting variables
before any tooling is built becomes desirable.
Today, numerical investigations of casting processes can be performed on both the
macroscopic and microscopic levels [2,3]. While macro-simulations allow the global
prediction of mold filling, solidification and stress formation, micro simulation seeks to
predict micro structural formation [4,5].
Heat conduction models are used in solidification simulation. The heat source in the
solidifying liquid is the latent heat of fusion released gradually as the solidification proceeds.

72 O.O. Oluwole, G.O. Oluwadare , A.A. Afonja Vol.7, No.1
Fraction of metal solidified per degree fall in temperature is a useful method of
calculating latent heat release during the solidification process [1-5]. Thermodynamic
data is used in calculating fraction of metal solidified during the solidification process which
in turn is used in calculating the latent heat of fusion release over the solidification range
[3,6]. Though thermodynamic data for most metals and their alloys are available in their
solid state, thermodynamic data for most multicomponent industrial alloys in the
solidification ranges are not available and are still an ongoing European collaborative
project [7,8].
Because of the non-availability of thermodynamic data, many researchers make use of
thermal equilibrium diagrams as alternatives. Though widely used, the thermal equilibrium
method is unreliable especially for multicomponent systems. Therefore there is still need to
develop an effective model for the release of latent heat of fusion over the solidification
range. In this present work a parabolic-elliptical model for latent heat release for the pro-
eutectic Aluminium Silicon-Magnesium alloy (AlSi7Mg) is developed.
2. MATERIALS AND METHODS
A curve of the cumulative weight fraction of metal solidified during fast solidification of
AlSi7Mg alloys is obtained by using thermodynamically formulated phase diagram,
generated by means of the code Thermocalc
TM
from Gieberei-Institut, RWTH-Aachen,
Germany. Using this plot, the curve is then fitted using appropriate equation and the
parameters of the plot. The mathematical equation obtained was then used to calculate
fraction solidified for the AlSi7Mg alloy and compared to the data from thermodynamic
data. The model was applied to AlSi7Mg alloy to determine ∆T. Fraction of solid data
generated from the results was compared to results obtained using thermodynamic data.
Results were verified used in solidification simulation using the Fourier equation
( )
t
T
CH
z
T
K
y
T
K
x
T
K
P
∂
∂
+∆=
∂
∂
+
∂
∂
+
∂
∂
ϕρ
2
2
2
2
2
2
and the Finite Difference Method of Numerical solution. The C Programming language
was used for writing the simulation codes[9] and Matlab used for graphics display.
The plot of the fraction of metal solidified is shown in Fig. 1. It shows two segments I
and II. Segment I shows an increase in weight fraction of metal solidified as temperature
drops until it gets to a temperature Te. This segment is parabolic. After Te, the
solidification does not proceed at a fixed temperature as would have occurred in the pro-
eutectic Al-Si binary alloy but increases elliptically in this second segment until it gets to
the segment where Mg
2
Si is formed in the solidifying alloy.

Vol.7, No.1 Development of Mathematical Equation 73
Fig.1. Shape of Cumulative Fraction of solid solidified
AlSi7Mg alloy under fast cooling conditions.
2.1 Modelling the Parabolic Component
The fraction solidified curve was thus divided into two segments: I and II. The parabolic
component is modelled after the parabola while the elliptic segment was modelled after
an ellipse. Equations of a parabola could be obtained in any pure mathematics text [10].
The general equation for a parabola is
y
2
= 4ax………………………………………………………………. (1)
Where x and y are the values on the x and y axis and a is the distance of the focus from
the axis close to the vertex.
If the parabolic segment in Fig.1 is extended to form a parabola, rotated, and placed on an
x-y axis as shown below (Fig.2). It can be seen that a provision for the vertex must be

74 O.O. Oluwole, G.O. Oluwadare , A.A. Afonja Vol.7, No.1
made for the parabola. This is shown as ∆T.
Fig.2: The Parabolic segment of Fig.1 extended to full parabola and rotated
Thus, y- axis is the cumulative weight fraction of metal solidified, fs, while the x-axis is
the Temperature, T in degrees Celsius.
Applying the general equation of the parabola to this curve will give
x –axis = Temperature axis, T (
o
C or K)
y-axis = fraction solidified axis; f
S
(
o
C or K)
a = measure of temperature (
o
C or K) from parabola theory (Bunday and Mulholand,
1975).
Thus the parabola becomes T
p
*
2
= 4af
pS
*.……………………………….. (2)
or 1
4
2*
=
PS
P
af
T
Thus
PS
P
af
T
4
2*
is a dimensionless factor
Where T
p
* = T
i
– T
E
+ ∆T where T
i
is the instantaneous temperature and T
E
is the
eutectic temperature and ∆T is the temperature needed for the curve to make its parabolic
turn at the vertex.

Vol.7, No.1 Development of Mathematical Equation 75
f
pS
* = f
Se
- f
Si
where f
Se
is the fraction solidified at the eutectic temperature and f
Si
is the
fraction solidified at Temperature T
i
.
a is the focus of the parabola which can be obtained at maximum T* and maximum f*.
Maximum T
P
* = T
L
+ ∆T - T
e
Maximum f
P
* = f
Se
∆T = temperature needed for the curve to make its parabolic turn at the vertex.
2.2 Modelling the Elliptic Component
The elliptic component of Fig. 1 can be modelled after a quadrant of an ellipse as shown
in Fig. 3 below.
Fig. 3 Elliptic component of Fig. 1 shown as a quadrant of an ellipse with major and
minor axis a and b respectively.
The general equation for an ellipse is 1
2
2
2
2
=+
b
y
a
x……………………….(3)
Applying this to the quadrant gives
1
)()1(
2
2*
22
2*
=
−
+
−
es
se TT
T
f
f………………………………………………….(4)
where f
se
= cumulative fraction solidified at Te
f* = f
S
- f
se
T* = T – Ts where Ts is the solidus temperature

76 O.O. Oluwole, G.O. Oluwadare , A.A. Afonja Vol.7, No.1
The Model
The Parabo-elliptic model can be stated as
At T > Te; i.e. Te < T< T
L
T
p
*
2
= 4a f
pS
* ……………………………………………………………….(5)
Where T
p
* = T
i
– T
e
+∆T where T
i
is the instantaneous temperature and T
e
is the
eutectic temperature.
f
pS
* = f
Se
- f
Si
where f
Se
is the fraction solidified at the eutectic temperature and f
Si
is the
fraction solidified at Temperature T
i
.
a is the focus of the parabola which can be obtained at maximum T* and maximum f*.
Maximum T
P
* = T
L
+ ∆T - T
e
Maximum f
P
* = f
Se
At TeT
≤
; i.e TeTTs
≤
≤
1
)()1(
2
2*
22
2*
=
−
+
−
es
se TT
T
f
f
……………………………………………….(6)
where f
se
= cumulative fraction solidified at Te
f* = f
S
- f
se
T* = T – Ts where Ts is the solidus temperature
2.3 Applying The Model
The model was applied to AlSi7Mg alloy solidifying in chilled mould. Fraction of solid
data generated from the results were used in numerical simulation of solidification
behaviour for un-risered casting. Riser size selected from the simulation was input back
into the program incorporating effect of riser.
3. RESULTS
3.1 Comparison of Model Results and Fraction of Solid From Thermodynamic Data
The parabo-elliptic model was used in calculating cumulative fraction of metal solidified
for AlSi7Mg alloy and compared to values obtained using thermodynamic data. These
are presented in Figs. 4 and 5. Regression analysis show no significant difference in the
results. The parabo-elliptic model equations applicable to AlSi7Mg are:
The Parabolic segment of the AlSi7Mg alloy

Vol.7, No.1 Development of Mathematical Equation 77
∆ T = 10; a = 1299.38; Equation of Parabola; T*
2
= 5197.5f*
f = 0.481 – f*; T = T*+ 565; Calculations were made at T* = 0,15,25,35,45,50
The elliptic segment
a = 15 ; b = 0.466; Equation of ellipse: 1
)469(.)18(
2
2
2
2
=+ yx
T = T* + 565; f = f* + 0.481;
Fig. 4: Cumulative Fraction of Metal solidified per deg. Celsius fall in
temperature for AlSi7Mg alloy .
Fig. 5: Fraction of metal solidified per deg. Celsius fall in
temperature for AlSi7Mg alloy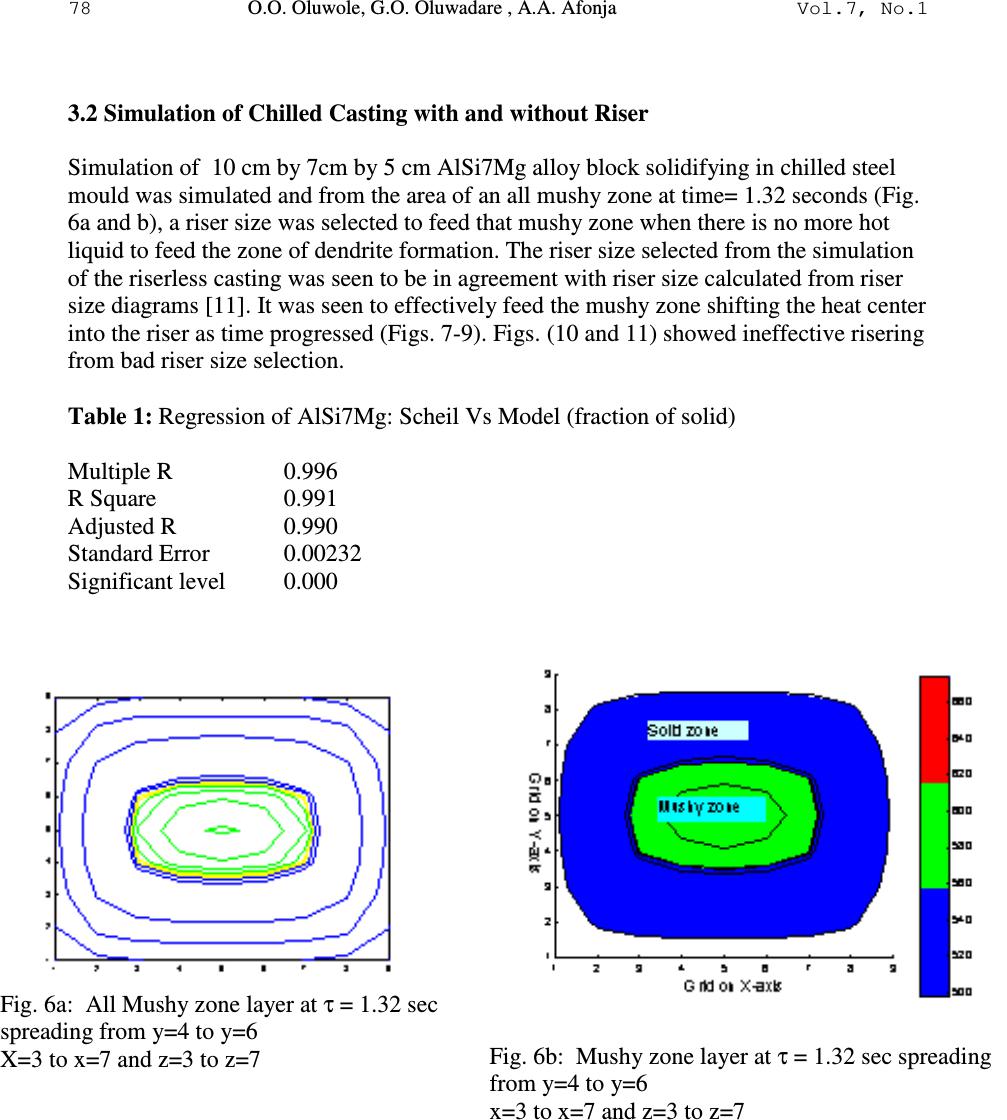

78 O.O. Oluwole, G.O. Oluwadare , A.A. Afonja Vol.7, No.1
3.2 Simulation of Chilled Casting with and without Riser
Simulation of 10 cm by 7cm by 5 cm AlSi7Mg alloy block solidifying in chilled steel
mould was simulated and from the area of an all mushy zone at time= 1.32 seconds (Fig.
6a and b), a riser size was selected to feed that mushy zone when there is no more hot
liquid to feed the zone of dendrite formation. The riser size selected from the simulation
of the riserless casting was seen to be in agreement with riser size calculated from riser
size diagrams [11]. It was seen to effectively feed the mushy zone shifting the heat center
into the riser as time progressed (Figs. 7-9). Figs. (10 and 11) showed ineffective risering
from bad riser size selection.
Table 1: Regression of AlSi7Mg: Scheil Vs Model (fraction of solid)
Multiple R 0.996
R Square 0.991
Adjusted R 0.990
Standard Error 0.00232
Significant level 0.000
Fig. 6a: All Mushy zone layer at τ = 1.32 sec
spreading from y=4 to y=6
X=3 to x=7 and z=3 to z=7
Fig. 6b: Mushy zone layer at τ = 1.32 sec spreading
from y=4 to y=6
x=3 to x=7 and z=3 to z=7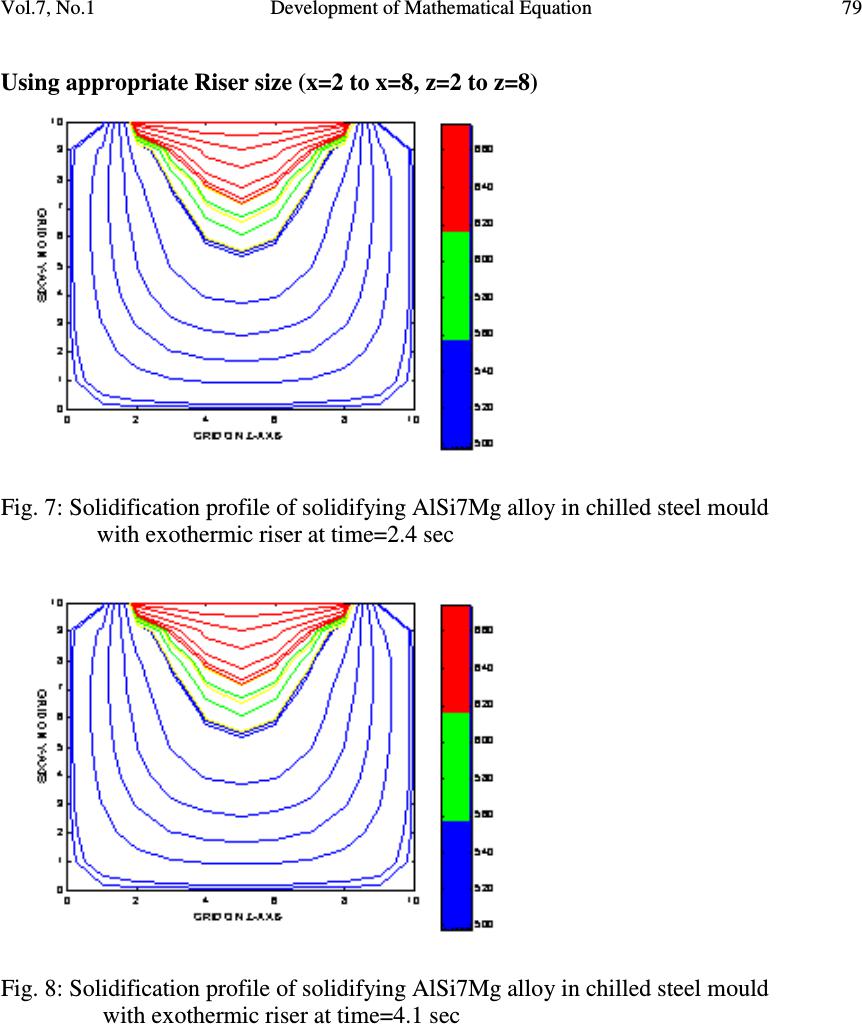

Vol.7, No.1 Development of Mathematical Equation 79
Using appropriate Riser size (x=2 to x=8, z=2 to z=8)
Fig. 7: Solidification profile of solidifying AlSi7Mg alloy in chilled steel mould
with exothermic riser at time=2.4 sec
Fig. 8: Solidification profile of solidifying AlSi7Mg alloy in chilled steel mould
with exothermic riser at time=4.1 sec

80 O.O. Oluwole, G.O. Oluwadare , A.A. Afonja Vol.7, No.1
Fig. 9: Solidification profile of solidifying AlSi7Mg alloy in chilled steel mould
with exothermic riser at time=13.3 secs
Using Incorrect Riser size (x=4 to x=6, z=4 to z=6)
Fig. 10: Solidification profile of solidifying AlSi7Mg alloy in chilled steel mould
with exothermic riser at time=1.2 secs using riser extending from x=4 to x=6

Vol.7, No.1 Development of Mathematical Equation 81
Fig. 11: Solidification profile of solidifying AlSi7Mg alloy in chilled steel mould
with exothermic riser at time=1.44 secs using riser extending from x=4 to
x=6
4. CONCLUSION
A model has been developed for fraction of solid solidified for AlSi7Mg alloy
solidification under fast cooling conditions that can effectively replace thermodynamic
data. Model is seen to effectively predict AlSi7Mg casting solidification.
REFERENCES
[1] Chen C. W., Li C. R., Han T. H., Shei C. T., Hwang W. S and C.M.Houng,
1994. Numerical Simulation of Filling Pattern for an Industrial Die Casting
and its Comparison with the defects distribution of an actual castings . Trans. of
the American Foundrymen’s Society , 102 , 139-146.
[2]Chen. Y. F. and W.S. Hwang, 1996. Mould Filling Simulation with Partial Cell
Method. Trans American Foundrymen's Society , 104 , 197-201.
[3] Fackeldy. M, Ludwig. A and P.R. Sahm,, 1996. Coupled Modelling of the
Solidification process predicting Temperature, Stresses and Microstructure
Computational Material Science , 7(194-199).
[4]Cheng C. Q., Upadhya G., Suri V. K., Atmakuri S and A.J Paul,1992.
Solidification Modelling and Prediction of Defect of a sand cast Ductile Iron T-
Plate. American Foudrymen Society. 20p
[5]Ehlen G. Schweizer A. Ludwig A. and P.R Sahm, 2000. Free Surface Model to
Predict the Influence of Shrinkage Cavities on the Solute Redistribution in
Castings In: Modeling of Casting, Welding and Advanced Solidification
Processes IX, ed. P.R. Sahm, P. N. Hansen, J. G. Conley, 632-63
[6]A. Ludwig,2001. Comparison of Dendrites of a pure Material with Thermal Alloy
Dendrites. Acta Materiala , 49 , 165.
[7]MEBSP,2002. Microstructural Engineering by solidification processing;
Properties base for Solidification Simuilation- European collaborative program”
http:// www.gi.rwth-aachen.de/MEBSP-b

82 O.O. Oluwole, G.O. Oluwadare , A.A. Afonja Vol.7, No.1
[8] Ludwig. A , Quested. B . and G.Neuer,2001. How to find Thermophysical Material
Property data for casting Simulations. Advanced. Engineering Materials, 3, 11
[9] Oluwole.O Ph.D Thesis, Obafemi Awolowo University, (2004) 266 pages.
[10] Bunday B . D and H. Mulholand (1975). Pure Mathematics for Advanced Level
Butterworths , London , 94 -129, 170 – 187.
[11] E. Myskowski, H. Bishop and W. PelliniT Riser Diagrams Trans. AFS, 63 (1955) 271.