Journal of Environmental Protection, 2010, 1, 155-171
doi:10.4236/jep.2010.12020 Published Online June 2010 (http://www.SciRP.org/journal/jep)
1
Analysis of Mean Monthly Rainfall Runoff Data of Indian
Catchments Using Dimensionless Variables by Neural Network
Manish Kumar Goyal*, Chandra Shekhar Prasad Ojha
Department of Civil Engineering, Indian Institute of Technology, Roorkee, India.
Received April 2nd, 2010; revised May 4th, 2010; accepted May 5th, 2010.
ABSTRACT
This paper focuses on a concept of using dimensionless variables as input and output to Artificial Neural Network
(ANN) and discusses the improvement in the results in terms of various performance criteria as well as simplification of
ANN structure for modeling rainfall-runoff process in certain Indian catchments. In the present work, runoff is taken as
the response (output) variable while rainfall, slope, area of catchment and forest cover are taken as input parameters.
The data used in this study are taken from six drainage basins in the Indian provinces of Madhya Pradesh, Bihar, Ra-
jasthan, West Bengal and Tamil Nadu, located in the different hydro-climatic zones. A standard statistical performance
evaluation measures such as root mean square (RMSE), Nash–Sutcliffe efficiency and Correlation coefficient were em-
ployed to evaluate the performances of various models developed. The results obtained in this study indicate that ANN
model using dimensionless variables were able to provide a better representation of rainfall–runoff process in com-
parison with the ANN models using process variables investigated in this study.
Keywords: Dimensional Variables, Artificial Neural Networks, Rainfall–Runoff
1. Introduction
The rainfall-runoff relationship is one the most complex
hydrological phenomenon due to the tremendous spatial
and temporal variability of watershed characteristics and
rainfall patterns as well as a number of variables in-
volved in the physical processes. Also, this process is
non-linear in nature and thus difficult to arrive at explicit
solutions [1,2]. The runoff needs to be estimated for effi-
cient utilization of water resources. The rainfall-runoff
models play a significant role in water resource man-
agement planning and hydraulic design. Several attempts
have been made to model the non-linearity of the rain-
fall–runoff process, arising from intrinsic non-linearity of
the rainfall–runoff process and from seasonality These
rainfall-runoff models generally fall into these broad
categories; namely, black box or system theoretical mod-
els, conceptual models and physically-based models
[3-5]. Black box models normally contain no physi-
cally-based input and output transfer functions and
therefore, are considered to be purely empirical models.
Conceptual rainfall-runoff models usually incorporate
interconnected physical elements with simplified forms,
and each element is used to represent a significant or
dominant constituent hydrologic process of the rain-
fall-runoff transformation [6,7]. A dimensional analysis
technique has also been developed and used to obtain
mean annual flood estimation in several Indian catch-
ments [8].
In recent year, applications of Artificial Neural Net-
work (ANN) has become increasing popular in water
resources and have been used in various fields for the
prediction and forecasting of complex nonlinear proc-
esses, including the rainfall runoff phenomenon. Many
studies have demonstrated that the ANNs are excellent
tools to model the complex rainfall–runoff process and
can perform better than the conventional modeling tech-
niques [1,9-12] However, many a times, less attention is
given to simplify the ANN structure.
The use of dimensionless variables as input and output
to ANN in rainfall-runoff modeling has not been found in
the literature as of our best knowledge. Although, some
evidences of using dimensionless variables in ANN are
known in application of estimation of scour downstream
[13] and for heat problems [14]. Swamee used the di-
mensionless variables to compute annual flood estima-
tion and hence, the same dimensionless variables are
used in this present study in the context of rainfall-runoff
process [8].
Thus, in view of the above, the objectives of the pre-
sent study are to 1) evaluate dimensional analysis tech-
nique of Swamee et al.; 2) investigate the technique of

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 156
ANNs using process variables as well as dimensionless
variables for modeling the complex rainfall–runoff proc-
ess; and 3) to achieve simplifications in ANN structure.
The paper begins with a brief introduction of the com-
puting techniques of ANN and study area followed by
the details of the model development before discussing
the results and making concluding remarks. The tech-
niques are applied on all river basin data used in the pre-
sent study and Damodar river basin is used as an exam-
ple of individual river basin to examine the effects on
individual catchment.
2. Artificial Neural Network
The Artificial Neural Network represents an alternative
computational paradigm where the solution to a problem
is learned from a set of samples. An artificial neural
network consists of simple synchronous element, called
neurons, which are analogous to the biological neurons in
the human brain [7,15]. These neurons are arranged in
layers in a network. The neurons in one layer are con-
nected to those in the adjacent layers and strength of
connection between the two neurons in adjacent layers is
called “weight”. There are weights on each of the inter-
connections and it is these weights that are altered during
the training process to ensure that the inputs produce an
output that is close to the desired value with an appropri-
ate training rule being used to adjust the weights in ac-
cordance with the data that are presented to the network.
An ANN normally consists of three layers, an input layer,
a hidden layer, and an output layer. In a feed-forward
network, the weighted connections feed activations only
in the forward direction from an input layer to the output
layer. Each node in a layer receives and processes
weighted input from a previous layer and transmits its
output to nodes in the following layer through links. A
typical three layer feed-forward network is shown in
Figure 1. There are many optimization techniques for
neural networks training using the backpropagation algo-
rithm. Recently, Levenberg–Marquardt learning algo-
rithms are used increasingly due to the better perform-
ance and learning speed with a simple structure [15,16].
Figure 1. Three layer feed-forward neural network
This learning algorithm is discussed here briefly as fol-
lows:
The Levenberg–Marquardt algorithm is based on ap-
proaching second-order training speeds without having
the computation of Hessian matrix [17]. The Leven-
berg–Marquardt algorithm uses an approximation to the
Hessian matrix in the following Newton-like update:
when μ is large, this becomes gradient descent with a
small step size, and when μ is small, the algorithm ap-
proximates the Newton’s method.
The Levenberg-Marquardt algorithm uses this ap-
proximation to obtain the revised weight in the following
form:
Xk + 1 = Xk – 1
[]
TT
J
JIJ 

e
(1)
where J is the Jacobian matrix that contains first deriva-
tives of the network errors with respect to the weights
and biases; e is a vector of network errors and I is an
identity matrix [15,18,19].
Study Area
The data used in this study are from 31 sub-catchments
of six large drainage basins in the Indian provinces of
Madhya Pradesh, Bihar, Rajasthan, West Bengal and
Tamil Nadu. Locations of the various catchments and
sub-catchments taken for the analysis are shown in Fig-
ure 2. The sub-catchments were grouped under six major
river basins namely Damodar, Barkar, Chambal, May-
urakshi, Lower Bhawani and Ram Ganga.
Figure 2. Geographical locations of different catchments

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 157
16
75
84
91
4
39
69
The values of monthly runoff were determined by
summing up the daily observed discharges for the month.
The monthly rainfall for each catchment was averaged
using the Theissen polygon method. The hydrological
data for use in the present study is taken from Pooja Jain
and Rama Raju [20,21]. These data were originally taken
from the reports of Soil and Water Conservation Division,
(1984, 1987) published by Water Conservation Division
of the Ministry of Agriculture, Government of India. The
periods for which data is available vary from 10 to 17
years. Some data points were excluded from published
hydrological data where runoff was more than precipita-
tion, which is practically not possible. Mean values of
several years of data are given in Table 1 and ranges of
the above mentioned data used in the present study are
given in Table 2.
Table 1. Mean value of data used
Hydrological
region
R
m
(mm)P
m
(mm)R
m
(mm) P
m
(mm) R
m
(mm)P
m
(mm) R
m
(mm)P
m
(mm)R
m
(mm) P
m
(mm)
42.62 97.67131.16282 95.32222 84.66206 31.4147.98.512 299.61
63.36165 151.8251 148.9263 130.218851.774.617.510 291.53
45.11 123.7 142.6 283.4 165.4 280.1123236.8 66.3 87.3 14.510 261.9
54 113.3 145.3 275.8 136.1285 131.5 228.649.974.612.515 172.88
49.6 132.11 128.16266177326.1 148.65229.157.390.241320 267.7
31.2 134.2 98.51240 190.6 327.7 150.5 231.240.750.912.828 69.62
78.9 155.5 99.85 224.1120 271.677.6 136.7 40.24 52.6416.530 396.99
51.72 159.41 131.26242 216.22301108.8197.857.8491.58.540 149.6
59140 142.2301 138.9 284.7127.64 223.775.3 107.612.535 441.54
22.7474.3113.81270135.18 263.7 139.9 280.5 46.54 86.411450 156.64
33.278.2 137.2 331.8 154.7306113 230.129.64611.540 235.87
72.7 166.6103.64 340.4159.25 299.6 126.7212.6 51.0460.6960 35.58
7.53 49.18 62.11230 112.7277.5 46.91 149.15.7312152 15.4
4.5 43.65 55.43 192.2129.71 232.8 37.311355.8811.3142
4.6 49.2288.2 235.1 114.627250.6 171.25.659.6840 29.2
19.774.5 109.6 266.7 97.45 238.1 50.16 132.46.16.16.51 383.2
11.1749.7 84.41 228.6120.71 286.159.7 193.510.964.61.515 345.65
45.46 134.5177.41 351.6 137.8 244.6152 271.6 58.11 81.41525 1514.45
31.5 110.6152.65 321.4143.06 261.2122.43 212.4 47.4271.61338 1054.47
60.8 175 142 362 154 220162.2225.648.1145.2826346.
40.54147 268.6 370.7 149.6 236.3171.23 245.840.8453.535 39.26
23.5 108.7149.21 307.4 107.1 221.5108 219.8 40.3547.5635 76.79
49.3 142.2 191.6351 133.8238130.16 236.23851.3448196.
25.8 108.8 131.2 390.4 196.1 257.8 150.7 223.2 44.2633.7645311.
34 130.7 118.1310 113.7 256.5128.1247.3 38.4 57.65.540 65.19
25.4165.6 23.7166.51545.246.4 149.2 77.42 196.2410019.4
19.11 82.9 37.6 65.111 53.8 19.3122.314.51147.48100 17.5
36.4 234.3 137.8 507.4 142.2 443.7 120.5 207.846.7 187.3565238.
128.2300 360.8 520.2 193.439975.9 346.893.2184488 89.1
28.75 194.7 58.72 481.4 106.2429100 231.341 120.1779144.
48.33 246.767.3 425.7 106.6 430.7 103.6 221.660.3 155.4569 90.75
Ram GangaMayurakshi
Lower Bhawa n i
FA(%) A(Km2)
DamodarBarakarChambal
June JulyAugSeptOct
S(%)
Table 2. Range of the data
Range
Sl.No. DATA
Minimum Maximum
1 Catchment Area(Km2) 15.4 1514.45
2 Monthly Runoff (mm) 4.5 360.8
3 Monthly rainfall(mm) 11.3 520.2
4 Land Slope (%) 1.0 17.5
5 Forest Cover (%) 1. 0 100

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 158
3. Methods
3.1 Dimensional Analysis
For dimensional analysis, Buckingham’s π theorem can
be used to obtain the various dimensionless groups [8].
Swamee has investigated the influence of inclusion of 4
dimensionless groups in mean flood flow estimation.
These dimensionless groups were formed using variables
such as discharge Q, Area A, average rainfall p, of dura-
tion D and recurrence interval T, Slope S and forest cover
FA [8].
Based on available data for Indian catchments, fol-
lowing variables were identified: rainfall (P), runoff (R),
slope (S) and forest cover (FA). Adopting A as the re-
peated variable, following nondimensional groups were
formed:
R* = A-0.5 R (2)
P* = A-0.5 P (3)
where R is the runoff in mm, P is the rainfall in mm and
A is the drainage area in km2.
Using the above dimensionless group, the following
empirical equation was proposed:
3 1
*0* 24
()( )
a a
A
RaPSa Fa 
5
a
5
)
a
(4)
Here a0-a5 are empirical constants, S is the slope (per-
cent) and FA is the forest cover.
The computed value for R* for ith data set R*ci was ob-
tained as
3 1
*0* 24
()(
a a
cii iAi
RaPSaFa (5)
Here suffix i stand for ith data set and a0-a5 are fitted
coefficients.
Using Equation (5), the observed value R* for ith data
set R*oi was obtained. To calibrate the model, the error
criterion was set to minimize the average percentage er-
ror Ea, defined as
**
1*
100 n
oi ci
ioi
RR
Ea nR


 (6)
3.2 ANN Model Development Using Process
Variables
Before the data presented to the ANN training, it must be
standardized in order to restrict its range to the interval [0,
1]. The actual observed outputs of the network being
outside this bounded range of neuron transfer function;
need to be normalized such that they fall within the
bounded output range. To develop a model, it is impor-
tant to establish a correlation between the dependent
variable with the independent variables. For this purpose,
correlation matrix has been made and is given in Table 3.
Using the information drawn from the correlation matrix
analysis, runoff models have been decided as a function
of different input variables. However, rainfall has been
considered as a common input variable among all.
1:( ){( )}
A
NNPAMR tfP t (7)
2:( ){( ),}
A
NNPAMR tfP tS (8)
3:( ){(),,}
A
ANNPAMR tfP tSF (9)
4:( ){( ),,,}
A
A
NNPAMRtfP tSFA

(10)
5:( ){(1),( ),,,}
A
A
NNPAMR tfP tPtSFA


Here ANNPAM represents Artificial Neural Network
Process variables All river basins Model.
The development of rainfall–runoff models using
ANNs, involves the following steps: 1) selection of data
set for training, cross-validation and validation of the
model, 2) identification of the input and output variables,
3) normalization of the data, 4) selection of the network
architecture, 5) determining the number of neurons in the
hidden layer, 6) training of the ANN models, and 7)
validation and cross-validation of ANN model using the
selected performance evaluation statistics.
Back Propagation Learning Network (BPLN) has been
first calibrated using about 60 percent of data and 20
percent of data have been used in the validation of model.
The remaining 20 percent have been used for cross vali-
dation of the model. The momentum coefficient is ada-
pted to 0.9 and learning rate is fixed to 0.05 for neural
network training. The number of epochs has been set to
3000. Log sigmoid is used as transfer function. The set of
inputs combination which produced desired results cor-
responding to minimum RMSE were adopted for further
analysis.
3.3 ANN Model Development Using
Dimensionless Variables
Following model ANNDAM1 has been developed using
dimensionless variables of rainfall (P*), slope (S), forest
cover (FA) and runoff (R*). These dimensionless vari-
ables are discussed previously. Here ANNDAM repre-
sents Artificial Neural Network Dimensionless All river
basin Model.
Table 3. Correlation matrix of the variables
Runoff Rainfall Slope Forest cover Area
Runoff 1.0000
Rainfall 0.7769 1.0000
Slope 0.1333 –0.0114 1.0000
Forest cover –0.1315 0.0891 –0.3675 1.0000
Area 0.1299 0.0405 0.1761 –0.3471 1.0000

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 159
1:*( ){*( ),,}
A
ANNDAMRtf PtSF (11)
2:*(){*(1),*( ),,}
A
ANNDAMR tfPtPtSF
(12)
Model-Performance Criteria
For identification of best combination of input vari-
ables, different models are tested using various perform-
ance criteria [22]. Root mean square error (RMSE) has
been calculated for training, validation and testing data of
these models. The RMSE is defined as follows.
2
1
()
N
ci
N
YY
RMSE N




(13)
In addition, the Nash–Sutcliffe efficiency (η) is also
widely used in water resources sector to assess the per-
formance of a model [23].
2
1
2
1
()
1
()
N
ic
i
N
i
i
YY
YY








(14)
Also the correlation coefficient (CC) was also used a
performance criteria and is computed by using the fol-
lowing relationship [22].
1
1()(
n
ic
i
yc yi
YYYYc
N
CC




)
(15)
where is observed output, is computed output,
Yc Y
Yis the mean of observed output , Yc is the mean of
computed output,

is the standard deviation and N is
total no. of samples.
4. Training and Validation and
Cross-Validation of Data
4.1 Training, Validation and Cross-Validation of
All River Basins Data
Data have been analyzed in this section using dimen-
sional analysis and ANN using process variables as well
as using dimensionless variables.
Using Dimensional Analysis Model
The dimension analysis model DAAM1 was developed
and fitted coefficients a0-a5 were calculated by minimiz-
ing Ea by using steepest descent technique. DAAM
represents Dimensional Analysis All river basins Model.
The optimum value of a0-a5 was obtained for which Ea
was 39.74. This yielded the following form of (5):
DAAM1: R* = 0.41P*0.89(S + 0.052)0.112(FA + 0.049)-0.001 (16)
By using above expression, for model DAAM1, RMSE
was 5.11, 4.05, 2.79 and Nash-Sutcliffe efficiency was
0.58, 0.45, and 0.73 as well as CC was 0.837, 0.729, and
0.910 for training, validation and cross validation set
respectively for. The performance statistics in terms of
RMSE, Nash-Sutcliffe efficiency and CC of the results
for this model have been summarized in Table 4. The
trends of the RMSE for different models have been
shown in Figure 3.
Using ANN with BPLVM Using Process Variables
Using the same input process variables defined as the
models (i.e. ANNPAM1 through ANNPAM5), the ANN
models have been trained using Levenberg-Marquardt
algorithm (BPLVM) for different ANN architectures.
The performance statistics of the results for all the models
used with different architectures have been summarized in
Tables 5(a)-(d). The trends of the RMSE for different
architectures have been shown in Figures 4(a)-(d).
Table 4. Summary of dimensional analysis to Model DAAM1
Training Validation Testing
Architecture RMSE η CC RMSE η CC RMSE η CC
DAAM1 5.1130.583 0.83744.0520.4500.72962.797 0.731 0.9104
Figure 3. RMSE of dimensional analysis for DAAM1

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 160
Table 5(a). Summary of ANN application to ANNPAM1 using BPLVM process variables
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
1-1-1 37.178 0.632 0.79530.5840.7040.84122.761 0.767 0.886
1-4-1 29.302 0.772 0.87830.9810.6960.84021.792 0.786 0.890
1-6-1 28.936 0.777 0.88228.9290.7350.86823.117 0.759 0.879
1-2-2-1 32.783 0.714 0.84529.6530.7220.85521.844 0.785 0.888
1-4-5-1 30.546 0.752 0.86729.8200.7180.85421.179 0.798 0.896
1-6-7-1 26.367 0.815 0.90329.9820.7150.84725.961 0.696 0.861
Table 5(b). Summary of ANN application to ANNPAM2 using BPLVM with process variables
Training Validation Testing
Network Ar-
chitecture RMSE η CC RMSE η CC RMSE η CC
2-1-1 36.4981 0.6455 0.80330.68280.70190.84419.9987 0.8198 0.911
2-4-1 35.7986 0.6590 0.81230.79230.69970.84121.6273 0.7893 0.900
2-6-1 26.7166 0.8101 0.90030.03520.71430.85536.0875 0.4132 0.772
2-2-2-1 29.1566 0.7738 0.88029.56810.72310.85424.7052 0.7250 0.863
2-4-5-1 28.1872 0.7886 0.88830.53160.70480.84628.8788 0.6242 0.828
2-6-7-1 24.4513 0.8409 0.91731.05850.69450.83526.5795 0.6817 0.844
Table 5(c). Summary of ANN application to ANNPAM3 using BPLVM with process variables
Training Validation Testing
Network Archi-
tecture RMSE
η CC
RMSE
η CC
RMSE
η CC
3-1-1 36.266 0.650 0.80629.9970.7150.84821.070 0.800 0.903
3-4-1 20.904 0.884 0.94033.9430.6350.80327.726 0.654 0.841
3-6-1 19.254 0.901 0.94935.6370.5980.80233.779 0.486 0.761
3-2-2-1 35.287 0.669 0.81830.3900.7080.84721.872 0.784 0.905
3-4-5-1 23.231 0.856 0.92527.4290.7620.87818.896 0.839 0.917
3-6-7-1 23.650 0.851 0.92332.8900.6570.81324.946 0.720 0.876
Table 5(d). Summary of ANN application to ANNPAM4 using BPLVM with process variables
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
4-1-1
36.2552 0.6502 0.80629.86380.71760.85020.9179 0.8029 0.905
4-4-1
23.3499 0.8549 0.92533.05060.65410.81022.6574 0.7687 0.884
4-6-1
18.7049 0.9069 0.95231.30370.68970.83523.8769 0.7431 0.867
4-2-2-1 28.7672 0.7798 0.88329.05590.73260.86219.3198 0.8318 0.912
4-4-5-1 34.3087 0.6868 0.82933.23600.65020.80724.3186 0.7335 0.886
4-6-7-1 19.2702 0.9012 0.95142.22420.43540.72030.8548 0.5711 0.792

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 161
Table 5(e). Summary of ANN application to ANNPAM5 using BPLVM with process variables
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
5-1-1 37.6870 0.4522 0.6729.52600.57060.7817.7127 0.3662 0.66
5-4-1 32.8048 0.5849 0.7656.1951–0.55530.2864.1959 –7.3250 0.36
5-6-1 8.6947 0.9708 0.99127.3057–6.9822–0.61142.9043 –40.253 –0.16
5-2-2-1 28.6140 0.6842 0.8327.90180.61660.8119.4920 0.2325 0.63
5-4-5-1 18.1824 0.8725 0.9344.78180.01230.6175.2239 –10.430 0.13
5-6-7-1 9.9741 0.9616 0.9896.0710–3.54580.51147.6428 –43.034 0.05
1) Model ANNPAM1: The performance of this model
has been presented in Table 5(a) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 4(a). For this model, RMSE was in the
range of 21.17-37.17 and Nash-Sutcliffe efficiency was
in the range of 0.632-0.815 for different NN architecture.
The best identified NN architecture was 1-4-5-1 for
which RMSE was in the range of 21.17-30.54 and
Nash-Sutcliffe efficiency was in the range of 0.718-0.798.
The NN architecture performed 1-1-1 the worst for
which RMSE was in the range of 22.76-37.17 and Nash-
Sutcliffe efficiency was in the range of 0.632-0.767.
2) Model ANNPAM2: The performance of this model
has been presented in Table 5(b) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 4(b). For this model, RMSE was in the
range of 19.99-36.49 and Nash-Sutcliffe efficiency was
in the range of 0.413-0.840 for different NN architecture.
The best identified NN architecture was 2-1-1 for which
RMSE was in the range of 19.99-36.49 and Nash-
Sutcliffe efficiency was in the range of 0.645-0.819. The
NN architecture 2-6-7-1 performed the worst for which
RMSE was in the range of 24.45-31.05 and Nash-
Sutcliffe efficiency was in the range of 0.694-0.840.
3) Model ANNPAM3: The performance of this model
has been presented in Table 5(c) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 4(c). RMSE was in the range of 18.89-
36.26 for different NN architecture for this model. The
best identified NN architecture was 3-4-5-1 for which
RMSE was in the range of 18.89-27.42 and Nash-Sut-
cliffe efficiency was in the range of 0.762-0.856.The NN
architecture 3-1-1 performed the worst for which RMSE
was in the range of 21.07-36.26 and Nash-Sutcliffe effi-
ciency was in the range of 0.650-0.800.
4) Model ANNPAM4: The performance of this model
has been presented in Table 5(d) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 4(d). RMSE was in the range of
18.70-36.25 for different NN architecture for this model.
The best identified NN architecture was 4-6-1 for which
RMSE was in the range of was 18.70-31.30 and Nash-
Sutcliffe efficiency was in the range of 0.689-0.907.The
NN architecture performed 4-1-1 the worst for which
RMSE was in the range of 20.19-36.25 and Nash-Sut-
cliffe efficiency was in the range of 0.650-0.803.
5) Model ANNPAM5: The performance of this model
has been presented in Table 5(e) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 4(e). RMSE was in the range of
8.69-147.64 for different NN architecture for this model.
The best identified NN architecture was 5-2-2-1 for
which RMSE was in the range of was19.40-28.61 and
Nash-Sutcliffe efficiency was in the range of 0.23-0.68.
Based on these results, it can be inferred that NN ar-
chitecture 4-6-1 performs the best for which RMSE was
18.70, 31.30, 23.87, Nash-Sutcliffe efficiency was 0.907,
0.689, 0.743 and CC was 0.95, 0.83, 0.86 for training,
validation and cross validation set respectively.
ANN with BPLVM Using Dimensionless Variable
Using the input dimensionless variables defined in the
model ANNDAM1 and ANNDAM2; the ANN models
have been trained using Levenberg-Marquardt algorithm
(BPLVM) for different ANN architectures. The per-
formance statistics of the results for all the models used
with different architectures have been summarized in
Tables 6(a) and (b). The trends of the RMSE for different
architectures have been shown in Figures 5(a) and (b).
1) Model ANNDAM1: The performance of this model
has been presented in Table 6(a) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 5(a). For this model ANNDAM1, RMSE
was in the range of 2.13-6.88 and Nash-Sutcliffe effi-
ciency was in the range of (–0.65)-0.927 for different NN
architecture. For NN architecture 3-1-1, RMSE was 2.86,
4.86 and 3.85 and Nash-Sutcliffe efficiency was 0.762,
0.209 and 0.489 for training, validation and cross valida-
tion set respectively. For NN architecture 3-3-1, RMSE
was 3.10, 6.60 and 6.93 and Nash-Sutcliffe efficiency
was 0.845, –0.460 and –0.657 for training, validation and

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 162
(a)
(b)
(c)
(d)

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network163
(e)
Figure 4. (a) RMSE of different ANN architecture using BPLVM for ANNPAM1; (b) RMSE of different ANN architecture
using BPLVM for ANNPAM2; (c) RMSE of different ANN architecture using BPLVM for ANNPAM3; (d) RMSE of differ-
ent ANN architecture using BPLVM for ANNPAM4; (e) RMSE of different ANN architecture using BPLVM for ANNPAM5
(a)
(b)
Figure 5. (a) RMSE of different ANN architecture using BPLVM for ANNDAM1; (b) RMSE of different ANN architecture
using BPLVM for ANNDAM2

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 164
Table 6(a). Summary of ANN application to ANNDAM1 using BPLVM with dimensionless variables
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
3-1-1 2.8679 0.7620 0.873 4.8603 0.2089 0.645 3.8523 0.4890 0.905
3-3-1 3.1098 0.8458 0.920 6.6037 –0.4604 0.618 6.9372 –0.6571 0.873
3-5-1 2.1393 0.9270 0.963 5.0977 0.1297 0.697 6.8841 –0.6318 0.869
Table 6(b). Summary of ANN application to ANNDAM2 using BPLVM with dimensionless variables
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
4-1-1 4.1198 0.7223 0.850 4.5203 0.3047 0.686 2.9293 0.3388 0.77
4-3-1 2.6301 0.8868 0.942 5.3015 0.0437 0.6393 3.7672 –0.0936 0.55
4-5-1 2.9652 0.8562 0.925 4.1604 0.4110 0.7385 3.7473 –0.0820 0.59
cross validation set respectively. For NN architecture
3-5-1, RMSE was 2.13, 5.09 and 6.88 and Nash-Sutcliffe
efficiency was 0.927, 0.129 and –0.632 for training, vali-
dation and cross validation set respectively.
2) Model ANNDAM2: The performance of this model
has been presented in Table 6(b) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 5(b). For this model ANNDAM2, RMSE
was in the range of 2.63-5.30 and Nash-Sutcliffe effi-
ciency was in the range of (–0.08)-0.88 for different NN
architecture. For NN architecture 4-1-1, RMSE was 4.11,
4.52 and 2.92 and Nash-Sutcliffe efficiency was 0.722,
0.304 and 0.338 for training, validation and cross valida-
tion set respectively. For NN architecture 4-3-1, RMSE
was 2.63, 5.30 and 3.76 and Nash-Sutcliffe efficiency
was 0.88, 0.043 and –0.0.093 for training, validation and
cross validation set respectively. For NN architecture
3-5-1, RMSE was 2.96, 4.16 and 3.74 and Nash-Sutcliffe
efficiency was 0.856, 0.411 and –0.082 for training, vali-
dation and cross validation set respectively.
Based on these overall results, it can be inferred that
model ANNDAM1 with NN architecture 3-1-1 performs
the best for which RMSE was 2.86, 4.86, 3.85, Nash-
Sutcliffe efficiency was 0.762, 0.209,0.489 and CC was
0.873,0.645,0.905 for training, validation and cross vali-
dation set respectively.
4.2 Training, Validation and Cross Validation of
Damodar River Basin Data
Data of Damodar river basin has been analyzed in this
section using dimensional analysis, ANN models using
process variables and ANN models using dimensionless
variables.
Using Dimensional Analysis Model
The dimension analysis model DAINM1 was devel-
oped and fitted coefficients a0-a5 were calculated by
minimizing Ea by using steepest descent technique.
DAINM represents Dimensional Analysis Individual river
basin Model. The optimum value of a0-a5 was obtained
for which Ea was 20.54. This yielded the following form
of (5):
DAINM1: R* = 0.42P*0.95(S + 0.052)0.112(FA + 0.049)-0.001
(17)
By using above expression, for model DAINM1,
RMSE was 1.72, 2.43 and 1.044; Nash-Sutcliffe effi-
ciency was 0.85, 0.65 and –0.21 and CR was 0.950, 0.970,
0.945 for training, validation and cross validation set
respectively for. The performance statistics in terms of
RMSE, Nash-Sutcliffe efficiency and CC of the results
for this model have been summarized in Table 7. The
trends of the RMSE for different models have been
shown in Figure 6.
Using ANN with BPLVM Using Process Variables
Using the input process variables defined as the mod-
els (i.e. ANNPAM1 through ANNPAM4), the ANN
models (ANNINPM1 to ANNINPM4) have been trained
using Levenberg-Marquardt algorithm (BPLVM) for
different ANN architectures for Damodar river basin.
ANNINPM represents Artificial Neural Network Indi-
vidual river basin Process variables Model. The per-
formance statistics of the results for all the models used
with different architectures have been summarized in
Tables 8(a)-(d). The trends of the RMSE for different
architectures have been shown in Figures 7(a)-(d).
1) Model ANNINPM1: The performance of this model
has been presented in Table 8(a) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 7(a). For this model, RMSE was in the
range of 7.01-51.12 and Nash-Sutcliffe efficiency was in
the range of (–1.31)-0.999 for different NN architecture.
The best identified NN architecture was 1-6-1 for which
RMSE was in the range of 7.01-32.57 and Nash-Sutcliffe

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 165
Table 7. Summary of dimensional analysis to Model DAINM1
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
DAINM1 1.72 0.852 0.950 2.43 0.650 0.970 1.04 –0.210 0.945
Table 8(a). Summary of ANN application to ANNINPM1 using BPLVM with process variables
Training Validation Testing
Network Ar-
chitecture RMSE
η CC
RMSE
η CC
RMSE
η CC
1-1-1 11.9073 0.9477 0.97436.2359–0.16250.78425.5472 0.7336 0.907
1-4-1 9.4568 0.9670 0.98332.26510.07830.81723.2351 0.7796 0.913
1-6-1 7.0183 0.9818 0.99132.57330.06060.53131.4172 0.5971 0.817
1-2-2-1 9.5547 0.9664 0.98338.1784–0.29050.76325.7522 0.7293 0.943
1-4-5-1 1.3961 0.9993 1.00032.57500.06050.81931.6387 0.5914 0.853
1-6-7-1 11.4890 0.9514 0.97551.1218–1.31390.40624.6394 0.7522 0.919
Table 8(b). Summary of ANN application to ANNINPM2 using BPLVM with process variables
Training Validation Testing
Network Ar-
chitecture RMSE η CC RMSE η CC RMSE η CC
2-1-1 10.224 0.961 0.98133.5560.0030.87123.205 0.780 0.911
2-4-1 4.919 0.991 0.99644.444–0.749–0.36237.777 0.417 0.667
2-6-1 3.367 0.996 0.99842.190–0.5760.34651.692 –0.091 0.425
2-2-2-1 8.617 0.973 0.98635.593–0.1220.82926.514 0.713 0.890
2-4-5-1 6.836 0.983 0.99141.678–0.5380.68629.581 0.643 0.864
2-6-7-1 5.796 0.988 0.99434.436–0.0500.73628.463 0.669 0.868
Table 8(c). Summary of ANN application to ANNINPM3 using BPLVM with process variables
Training Validation Testing
Network Ar-
chitecture RMSE η CC RMSE η CC RMSE η CC
3-1-1 9.5579 0.9663 0.98332.59600.05930.84726.3721 0.7161 0.878
3-4-1 4.7262 0.9918 0.99635.7375–0.13080.62631.9391 0.5836 0.861
3-6-1 3.2147 0.9962 0.99835.6086–0.12260.90241.9146 0.2829 0.736
3-2-2-1 53.7743 –0.0657 0.03732.78910.04810.29647.5421 0.0774 0.285
3-4-5-1 34.0421 0.5729 0.84131.19960.13820.80050.3999 –0.0369 0.774
3-6-7-1 57.9588 –0.2380 0.02039.3340–0.36980.44061.3259 –0.5352 –0.559
Table 8(d). Summary of ANN application to ANNINPM4 using BPLVM with process variables
Training Validation Testing
Network Ar-
chitecture RMSE η CC RMSE η CC RMSE η CC
4-1-1 15.1078 0.9159 0.96216.56110.75720.94514.6386 0.9125 0.957
4-4-1 9.8741 0.9641 0.9836.70220.96020.98412.1456 0.9398 0.973
4-6-1 8.3123 0.9745 0.9886.60950.96130.98911.2242 0.9486 0.976
4-2-2-1 12.9961 0.9378 0.97012.67380.85780.94010.0796 0.9585 0.989
4-4-5-1 8.8720 0.9710 0.98610.51890.90200.95413.0449 0.9305 0.975
4-6-7-1 11.8970 0.9478 0.97817.22260.73740.96417.4376 0.8759 0.936

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 166
Figure 6. RMSE of dimensional analysis for DAINM1
(a)
(b)
(c)

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 167
(d)
Figure 7. (a) RMSE of different ANN architecture using BPLVM for ANNINPM1; (b) RMSE of different ANN architecture
using BPLVM for ANNINPM2; (c) RMSE of different ANN architecture using BPLVM for ANNINPM3; (d) RMSE of dif-
ferent ANN architecture using BPLVM for ANNINPM4
efficiency was in the range of 0.06-0.981. The NN archi-
tecture performed 1-6-7-1 the worst for which RMSE
was in the range of 11.48-51.12 and Nash-Sutcliffe effi-
ciency was in the range of (–1.31)-0.951.
2) Model ANNINPM2: The performance of this model
has been presented in Table 8(b) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 7(b). For this model, RMSE was in the
range of 3.36-51.69 and Nash-Sutcliffe efficiency was in
the range of (-0.749)-0.988 for different NN architecture.
The best identified NN architecture was 2-6-7-1 for
which RMSE was in the range of 5.79-34.43 and
Nash-Sutcliffe efficiency was in the range of (–0.05)
-0.988. The NN architecture 2-1-1 performed the worst
for which RMSE was in the range of 10.22-33.55 and
Nash-Sutcliffe efficiency was in the range of 0.003-
0.961.
3) Model ANNINPM3: The performance of this model
has been presented in Table 8(c) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 7(c). RMSE was in the range of 3.21-
61.32 for different NN architecture for this model. The
best identified NN architecture was 3-6-1 for which
RMSE was in the range of 3.21-41.91 and Nash-Sutcliffe
efficiency was in the range of (–0.122)-0.996. The NN
architecture 3-1-1 performed the worst for which RMSE
was in the range of 39.3-61.32 and Nash-Sutcliffe effi-
ciency was in the range of 0.059-0.966.
4) Model ANNINPM4: The performance of this model
has been presented in Table 8(d) and RMSE of the re-
sults for training, validation and cross-validation are
shown in Figure 7(d). RMSE was in the range of 6.60-
17.43 for different NN architecture for this model. The
best identified NN architecture was 4-6-1 for which
RMSE was in the range of was 6.6-11.22. The NN archi-
tecture performed 4-1-1 the worst for which RMSE was
in the range of 14.63-16.56.
Based on these results, it can be inferred that NN ar-
chitecture 4-6-1 performs the best for which RMSE was
8.31, 6.60, 11.22, Nash-Sutcliffe efficiency was 0.974,
0.961, 0.948 and CC was 0.988, 0.989, 0.976 for training,
validation and cross validation set respectively.
ANN with BPLVM Using Dimensionless Variable
Using the dimensionless variables as input defined in
the model ANNDAMI, the ANN model ANNINDM1 have
been trained using Levenberg-Marquardt algorithm (BPLVM)
for different ANN architectures. ANNINDM represents
Artificial Neural Network Individual river basin Dimen-
sionless variables Model. The performance statistics of
the results for all the models used with different archi-
tectures have been summarized in Table 9. The trends of
the RMSE for different architectures have been shown in
Figure 8.
For this model ANNINDM1, RMSE was in the range
of 0.344-3.36; Nash-Sutcliffe efficiency was in the range
of 0.198-0.995 and CC was in the range of 0.73-0.99 for
different NN architecture.
For NN architecture 3-1-1, RMSE was 1.16, 1.95 and
2.5 and Nash-Sutcliffe efficiency was 0.943, 0.198 and
0.786 for training, validation and cross validation set
respectively.
For NN architecture 3-3-1, RMSE was 0.815, 1.81 and
3.04 and Nash-Sutcliffe efficiency was 0.972, 0.314 and
0.683 for training, validation and cross validation set
respectively.
For NN architecture 3-5-1, RMSE was 0.34, 1.65 and
3.36 and Nash-Sutcliffe efficiency was 0.995, 0.426 and
0.614 for training, validation and cross validation set

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 168
Figure 8. RMSE of different ANN architecture using BPLVM for ANNINDM1
Table 9. Summary of ANN application to ANNINDM1 using BPLVM with dimensionless variables
Training Validation Testing
Network Archi-
tecture RMSE η CC RMSE η CC RMSE η CC
3-1-1 1.1645 0.9435 0.9711.95700.19820.7372.5000 0.7869 0.946
3-3-1 0.8154 0.9723 0.9861.81010.31410.8943.0480 0.6833 0.881
3-5-1 0.3446 0.995048 0.9981.65570.42610.8183.3638 0.6143 0.830
respectively.
Based on these results, it can be inferred that NN ar-
chitecture 3-1-1 performs the best for which RMSE was
1.16, 1.95 and 2.5; Nash-Sutcliffe efficiency was 0.943,
0.198 and 0.786 and CC was 0.971, 0.737 ,0.946 for
training, validation and cross validation set respectively.
5. Results and Discussion
Here is summary of results for all river basins data as
well as Damodar river basin data using different tech-
niques.
All River Basins
ANN models using process variables have been de-
veloped using all river basin data and the best identified
NN architecture was 4-6-1 of model ANNPAM4 for
which RMSE was in the range of 18.70-31.30 and Nash-
Sutcliffe efficiency was in the range of 0.689-0.907
while RMSE was in the range of 2.79-5.11, Nash-Sut-
cliffe efficiency was 0.45-0.73 and CC was in the range
of 0.729-0.910 for model DAAM1 using dimensional
analysis technique. Hence, it can be concluded that di-
mensional analysis technique performed better than ANN
models using process variables for all river basins data.
Based on the performance evaluation of ANN models
using dimensionless variables, ANNDAM1 performed
better than model ANNPAM4 using all river basin data in
terms of performance criteria. For this model ANNDAM1,
RMSE was in the range of 2.13-6.88 while RMSE was in
the range of 18.70-31.30 for ANNPAM4 using ANN
models with process variables. For best identified struc-
ture 3-1-1 with model ANNDAM1, RMSE was in range
of 2.86-4.86, Nash-Sutcliffe efficiency was in the range
of 0.20-0.90 and CC was in the range of 0.64-090. Hence,
it can be concluded that ANN models using dimen-
sionless variables performed better than Ann models us-
ing process variables for all river basins data. The com-
parison of observed and computed runoff for models
ANNPAM4 and ANNDAM1 have been shown in Figure 9
and Figure 10 respectively.
It is important to note here that the ANN architecture
of best identified model ANNPAM4 using process vari-
ables was 4-6-1 while ANN architecture of best identi-
fied model ANNDAM1 using dimensionless variables
was 3-1-1. Hence it can be concluded that ANN structure
can be simplified using dimensionless variables.
In this analysis of given data set, it has been found that
there was not much improvement in performance criteria
by using input process variable as P(t-1). For best identi-
fied model ANNPAM5 with NN architecture 5-2-2-1 us-
ing P(t-1) as one of input variables, RMSE was the range
of 19.40-28.61 while RMSE was in range of 18.70-31.30
for the best identified model ANNPAM4 with NN archi-
tecture 4-6-1 without using P(t-1) as a one of input proc-
ess variable. Similarly, for ANN model ANNDAM2 with
NN architecture 4-1-1 using P(t-1) as one of input di-
mensionless variables, RMSE was in the range of
2.92-4.52 while for ANN model ANNDAM1 with NN
architecture 3-1-1 without using P(t-1), RMSE was in the
range of 2.86-4.86.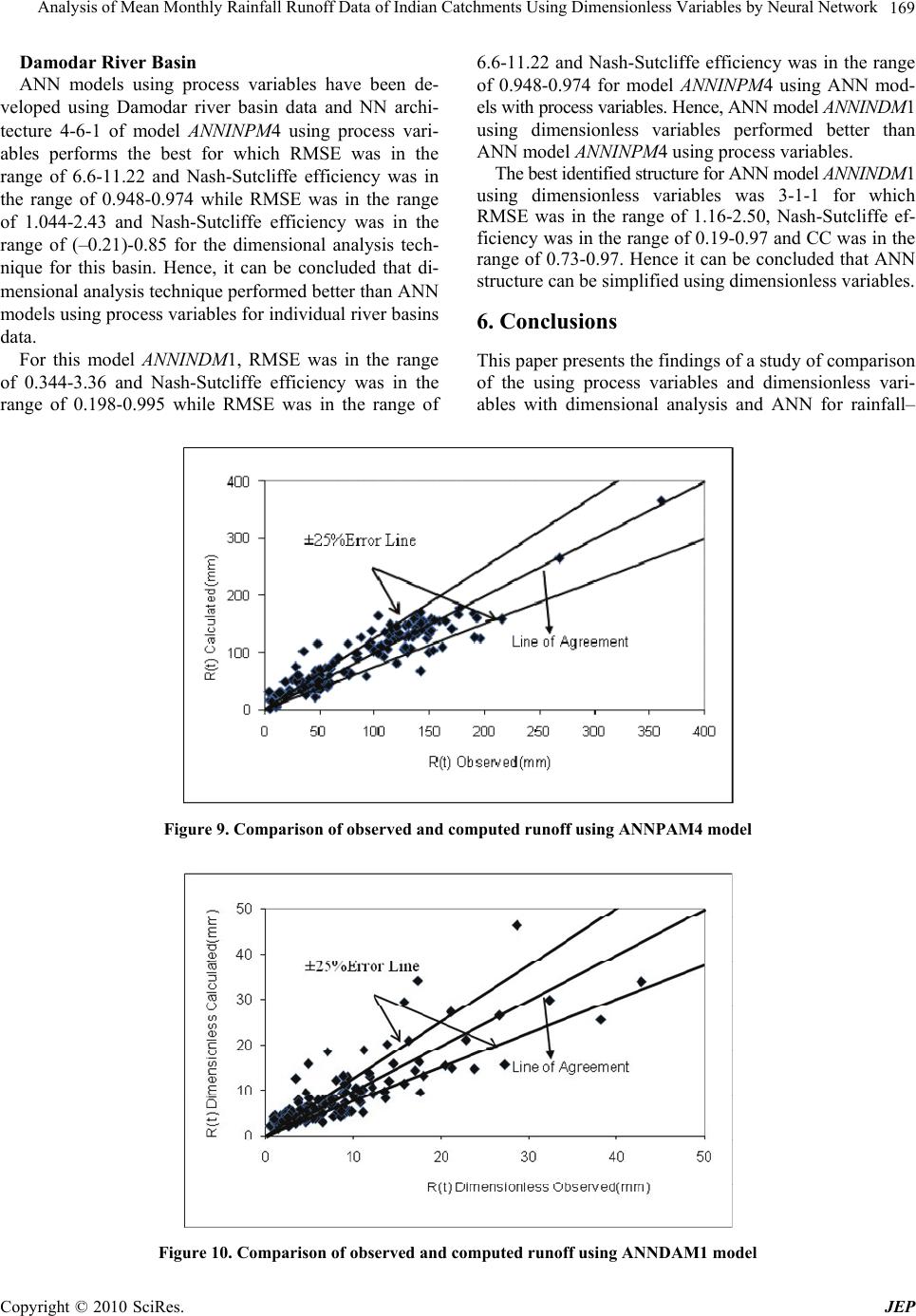

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network169
Damodar River Basin
ANN models using process variables have been de-
veloped using Damodar river basin data and NN archi-
tecture 4-6-1 of model ANNINPM4 using process vari-
ables performs the best for which RMSE was in the
range of 6.6-11.22 and Nash-Sutcliffe efficiency was in
the range of 0.948-0.974 while RMSE was in the range
of 1.044-2.43 and Nash-Sutcliffe efficiency was in the
range of (–0.21)-0.85 for the dimensional analysis tech-
nique for this basin. Hence, it can be concluded that di-
mensional analysis technique performed better than ANN
models using process variables for individual river basins
data.
For this model ANNINDM1, RMSE was in the range
of 0.344-3.36 and Nash-Sutcliffe efficiency was in the
range of 0.198-0.995 while RMSE was in the range of
6.6-11.22 and Nash-Sutcliffe efficiency was in the range
of 0.948-0.974 for model ANNINPM4 using ANN mod-
els with process variables. Hence, ANN model ANNINDM1
using dimensionless variables performed better than
ANN model ANNINPM4 using process variables.
The best identified structure for ANN model ANNINDM1
using dimensionless variables was 3-1-1 for which
RMSE was in the range of 1.16-2.50, Nash-Sutcliffe ef-
ficiency was in the range of 0.19-0.97 and CC was in the
range of 0.73-0.97. Hence it can be concluded that ANN
structure can be simplified using dimensionless variables.
6. Conclusions
This paper presents the findings of a study of comparison
of the using process variables and dimensionless vari-
ables with dimensional analysis and ANN for rainfall–
Figure 9. Comparison of observed and computed runoff using ANNPAM4 model
Figure 10. Comparison of observed and computed runoff using ANNDAM1 model

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network 170
runoff modeling in certain Indian catchments for a group
of river basins as well as individual basin. The perform-
ance of each model structure was evaluated using com-
mon performance criteria. The salient findings of this
study are presented as follows: 1) ANN models using
dimensionless variables performed better than ANN
models using process variables for all river basin data as
well as individual river basin data; 2) ANN models using
dimensionless variables simplified ANN architecture for
all river basins as well as individual river basin; 3) Di-
mensional analysis approach can be effectively used in
rainfall-runoff modeling.
REFERENCES
[1] M. N. French, W. F. Krajewski and R. R. Cuykendall,
“Rainfall Forecasting in Space and Time Using a Neural
Network,” Journal of Hydrology, Vol. 137, No. 1-4, Au-
gust 1992, pp. 1-31.
[2] N. Karunanithi, W. J. Grenney, D. Whitley and K. Bovee,
“Neural Networks for River Flow Prediction,” Journal of
Computing in Civil Engineering, Vol. 8, No. 2, April 1994,
pp. 201-220.
[3] J. C. I. Dooge, “Problems and Methods of Rainfall-Run-
off Modeling,” Mathematical Models for Surface Water
Hydrology: The Workshop Held at the IBM Scientific
Center, Pisa, 9-12 December 1977, pp. 71-108.
[4] S. Harun, N. I. Nor and A. H. M. Kassim, “Artificial
Neural Network Model for Rainfall-Runoff Relationship,”
Jurnal Teknologi B, Vol. 37, 2002, pp. 1-12.
[5] M. P. Rajurkar, U. C. Kothyari and U. C. Chaube, “Mod-
eling of the daily rainfall-runoff relationship with artifi-
cial neural network,” Journal of Hydrology, Vol. 285, No.
1-4, 2004, pp. 96-113.
[6] K. M. O’Connor, “Applied Hydrology Deterministic,”
Unpublished Lecture Notes, Department of Engineering
Hydrology, National University of Ireland, Galway, 1997.
[7] S. Sanaga and A. Jain, “A Comparative Analysis of Train-
ing Methods for Artificial Neural Network Rainfall–
Runoff Models,” Applied Soft Computing, Vol. 6, No. 3,
2006, pp. 295-306.
[8] P. K. Swamee, C. S. P. Ojha and A. Abbas, “Mean An-
nual Flood Estimation,” Journal of Water Resources Plan-
ning and Management, Vol. 121, No. 6, 1995, pp. 403-407.
[9] M. Campolo, P. Andreussi and A. Soldati, “River Flood
Forecasting with Neural Network Model,” Water Re-
source Research, Vol. 35, No. 4, 1999, pp.1191-1197.
[10] B. Zhang and R. S. Govindaraju, “Prediction of Water-
shed Runoff Using Bayesian Concepts and Modular Neu-
ral Networks,” Water Resource Research, Vol. 36, No. 3,
2000, pp. 753-762.
[11] A. Jain and S. Srinivasulu, “Development of Effective
and Efficient Rainfall–Runoff Models Using Integration
of Deterministic, Real-Coded Genetic Algorithms, and
Artificial Neural Network Techniques,” Water Resource
Research, Vol. 40, No. 4, 2004, p. 12.
[12] D. N. Kumar, M. J. Reddy and R. Maity, “Regional Rain-
fall Forecasting Using Large Scale Climate Teleconnec-
tions and Artificial Intelligence Techniques,” Journal of
Intelligent Systems, Vol. 16, No. 4, 2007, pp. 307-322.
[13] H. M. Azmathullah, M. C. Deo and P. B. Deolalikar, “Neu-
ral Networks for Estimation of Scour Downstream of a
Ski-Jump Bucket,” Journal of Hydraulic Engineering,
Vol. 131, No. 10, 2005, pp. 898-908.
[14] L. M. Tam, A. J. Ghajar and H. K. Tam, “Contribution
Analysis of Dimensionless Variables for Laminar and
Turbulent Flow Convection Heat Transfer in a Horizontal
Tube Using Artificial Neural Network,” Heat Transfer
Engineering, Vol. 29, No. 9, 2008 , pp. 793-804 .
[15] M. Aqil, I. Kita, A. Yano and S. Nishiyama, “Compara-
tive Study of Artificial Neural Networks and Neuro-
Fuzzy in Continuous Modeling of the Daily and Hourly
Behaviour of Runoff,” Journal of Hydrology, Vol. 337,
No. 1-2, 2007, pp. 22-34.
[16] S. M. A. Burney, T. A. Jilani and C. Ardil, “Levenberg-
Marquardt Algorithm for Karachi Stock Exchange Share
Rates Forecasting,” Proceedings of World Academy of
Science, Engineering and Technology, Vol. 3, 2005, pp.
171-176.
[17] H. Demuth and M. Beale, “Neural Network Toolbox for
Use with MATLAB, Users Guide,” Version 3, The Math-
Works, Inc., Natick, 1998.
[18] M. T. Hagan and M. B. Menhaj, “Training Feedforward
Networks with the Marquardt Algorithm,” IEEE Trans-
actions on Neural Networks, Vol. 5, No. 6, 1994, pp. 989-
993.
[19] K. Özgur, “Multi-Layer Perceptrons with Levenberg-Mar-
quardt Training Algorithm for Suspended Sediment Con-
centration Prediction and Estimation,” Hydrological Sci-
ences Journal, Vol. 49, No. 6, 2004, pp. 1025-1040.
[20] P. Jain, “Modeling of Monthly Rainfall-Runoff Process
Using ANN,” Master of Technology Dissertation, De-
partment of Civil Engineering, Indian Institute of Tech-
nology, Roorkee, 2004.
[21] V. R. Raju, “Estimation of Monthly Runoff,” Master of
Technology Dissertation, Department of Civil Engineer-
ing, University of Roorkee, Roorkee, 1998.
[22] S. K. Jain, P. C. Nayak and K. P. Sudheer, “Models for
Estimating Evapotranspiration Using Artificial Neural Net-
works, and their Physical Interpretation,” Hydrological
Processes, Vol. 22, No. 13, 2008, pp. 2225-2234.
[23] J. E. Nash and J. V. Sutcliffe, “River Flow Forecasting
through Conceptual Models, Part 1—A Discussion of Prin-
ciples,” Journal of Hydrology, Vol. 10, No. 3, 1970, pp.
282-290.

Analysis of Mean Monthly Rainfall Runoff Data of Indian Catchments Using Dimensionless Variables by Neural Network171
Appendices
I. Weights and Biases for BPLVM for model ANNPAM4 of network 4-6-1
Weights h11 h12 h13 h14 h15 h16
i1 –8.3602 –7.0334 8.6534 14.8352 1.5456 –0.6111
i2 –0.8806 17.6871 –17.5475 0.4825 –16.341 –6.7221
i3 0.331 0.3924 –0.375 –1.788 0.8711 –5.5499
i4 1.6462 5.0854 –5.5293 –8.3826 0.4748 –1.7737
Biases b11 b12 b13 b14 b15 b16
2.6117 1.2753 –1.7664 –1.1091 –2.5924 11.2949
II. Weights and Biases for BPLVM for model ANNDAM1 of network 3-1-1
Weights h11
i1 2.3092
i2 0.4151
i3 0.2383
Biases b11
8.9379
Biases bo1
1.0063e+003
Input layer 3nodes
Hidden layer 1nodes
Output layer 1 node
Weights O1
h21 –0.7559
h22 –4.2063
h23 –3.1118
h24 –0.3359
h25 –4.7739
h26 1.1961
Input layer 4nodes
Hidden layer 6 nodes
Output layer 1 node
Biases bo1
–3.855
Weights O1
h21 –1.0064e+003