Journal of Minerals & Materials Characterization & Engineering, Vol. 6, No.2, pp 121-134, 2007
jmmce.org Printed in the USA. All rights reserved
121
Numerical Computations to Produce Cokeable Coal
Blends at The Ajaokuta Steel Plant, Nigeria
1
A.O. ADELEKE, and
2
P. ONUMANYI
1
DEPARTMENT OF MATERIALS SCIENCE AND ENGINEERING,
OBAFEMI AWOLOWO UNIVERSITY, ILE-IFE, NIGERIA
2
DEPARTMENT OF MATHEMATICS,
UNIVERSITY OF JOS,JOS, NIGERIA
ABSTRACT
A mathematical model and its associated numerical search algorithm has been
developed for routine coal blending to include local coals for cokemaking at the
Nigerian blast furnace-based Ajaokuta Steel Plant. A typical binary blend proposed
using the model includes 28.38% and 29.00% of the ash- laden Lafia and non-caking
Okaba coals, respectively. The proposed blends satisfy basic chemical and mechanical
strength requirements at the lowest cost per ton of coal. The blending calculations
showed that only low ash, low sulphur, medium volatile and high vitrinite reflectance
prime grade coals such as the UK Ogmore should be imported for blending with the
ash-laden medium coking Lafia coal. When the proposed blends are successfully
confirmed with bench and pilot scale carbonization tests, cokemaking at Ajaokuta will
be conducted with substantial savings in foreign exchange.
Keywords: model, coal, blending, cokemaking, blast furnace

122 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
1.0 INTRODUCTION
Metallurgical coke is a solid coherent and brittle material obtained by carbonizing
bituminous prime coking coals in the coke oven plant. In the blast furnace, coke serves
as a reducing agent and supply the major part of the heat required for the ironmaking
process. It is also the only solid material below the smelting zone and thus supports the
overlying burden and provides a permeable column for reducing gases [1]. The
bituminous prime coking coals suitable for straight carbonization accounts for only
about 5% of the world’s supply of coals [2]. This problem has made blend
carbonization of prime coking coals with poorly coking coals a common practice
worldwide.
The Nigerian local coal deposit is estimated to be about 1.5 billion tons. Unfortunately,
tests conducted on these coal deposits showed that most of them are non-caking. Lafia
coal, the only local coal with good coking properties, is however, laden with excessive
ash and sulphur contents of about 26.30% and 2.30%, respectively [3]. The Lafia coal
deposit has been found to be geologically faulty and the minimum estimated cost of
mining it per ton was put at N87.50 as at 1977 [3]. Considering the present exchange
rate of the Nigerian Naira to the US dollar, the current mining price per ton of Lafia
coal can be taken to be US$ 87.50.
For cokemaking, coal blends are required to have specified range of values for volatile
matter, ash and sulphur contents [4]. Excessive ash increases the volume of slag in the
blast furnace, and reduces its operating efficiency. Sulphur in the coke gets into the
iron and reduces its mechanical strength, while very high volatile generally reduce coke
output [5] .
On completion of its first phase, Ajaokuta steel plant is expected to import its 1.3
million tons of coking coals annually. Considering the huge sum in foreign exchange
required, there is an urgent need to obtain cokeable blends including appreciable
amounts of local coals. The current high international price of about US$ 300 for
coking coals per ton makes coal blending optimization and co-carbonisation with
cheaper poorly coking coals more urgent [6]. Blend formulations by numerical
computations on the basis of a mathematical model have been employed in the steel
industries [7, 8].
The analysis results on Nigerian coals (i.e Okaba and Lafia) were obtained from the
tests conducted at the National Metallurgical Development Centre (NMDC), Jos,
Nigeria. The analysis data on the UK Ogmore and the Canadian coals were obtained
from literature [9, 10]. The values of average vitrinite reflectance were estimated for
coals for which it was not available from a curve of Rmax versus volatile matter (daf)
[11]. The prices per ton of coals used in the calculations were estimated based on
information obtained from literature [6, 12].

Vol.6, No.2 Numerical Computations to Produce Cokeable Coal Blends 123
In the bisection method, an appropriate value for the exact solution of a non-linear
equation f(x)=0 in the interval [a,b] of interest is obtained by a systematic reduction of
this interval through a process of successive halving of the interval containing the
desired root[13]. The aim of this research paper is to apply the concept of bisection
search to obtain blend mixtures of high and low grade coals that will meet the
specifications for metallurgical cokemaking at the Nigerian Ajaokuta Steel Plant.
2.0 THEORETICAL ANALYSIS
2.1 Co-ordinate Geometry
Analytical geometry refers to the representation of the points in the dimensional space
by ordered set of n or more numbers, called co-ordinates [14]. In two-dimensional
geometry (X – Y axes), the position of a point in a plane may be specified by its
distances from two fixed perpendicular lines; the axes. The Cartesian co-ordinates are
also called rectangular co-ordinates. There are also affine co-ordinates where three
axial planes meet by pairs in three axes OX, OY and OZ. In solid geometry, we deal
with solids such as a sphere, pyramid and a cylinder. A sphere is a solid such that every
point on its surface is at an equal distance from the same point, its centre. In space
geometry, sphere corresponds to a circle in plane geometry. The locus of a point is the
path traced out by a point, which moves under certain conditions. The point may move
in a plane or in space, and the Cartesian equation of the locus can be obtained; that is,
the connection which exists between X and Y, or (X,Y,Z in space), the co-ordinates of
the point referred to perpendicular axes.
2.2 Mathematical Modeling
Basically, mathematical modeling uses analogy to aid the understanding of complex
systems. Analogy helps to explain unfamiliar situations. Modeling affords the
opportunity to refine and improve our qualitative and quantitative understanding of a
particular system or process. In the design of new, larger or otherwise modified existing
processes or systems, mathematical modeling has proved invaluable in a large number
of industries [15].
Using linear programming, the coal blending problem can be formulated
mathematically as follows:
Minimize:
C = X
1
C
1
+ X
2
C
2
+ C
3
+ … + X
n
C
n
Subject to:
X
1
R
1
+ X
2
R
2
+ X
3
R
3
+ … + X
n
R
n
> 1.15 (1)

124 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
X
1
V
1
+ X
2
V
2
+ X
3
V
3
+… +X
n
V
n
> 30.3 (2)
X
1
V
1
+ X
2
V
2
+ X
3
V
3
+… +XnVn < 27.7 (3)
X
1
S
1
+ X
2
S
2
+ X
3
S
3
+… +X
n
S
n
< 0.9 (4)
X
1
A
1
+ X
2
A
2
+X
3
A
3
+… +X
n
S
n
< 10 (5)
X1+X2+. . . +X
n
= 1 (6)
Where:
X
1
,X
2
, . . . X
n
= are proportions of coals 1,2,. . .n in blend
R = vitrinite reflectance of coal
V = volatile matter content
S = sulphur content
A = Ash content
C = cost per ton of coal
2.3 Application of Co-ordinate Geometry to Coal Blend Formulations
Plane and space geometries can be used to represent various blend formulations.
2.3.1 Binary Blend Formulations
A binary blend must satisfy the following conditions:
i. It consists of two coals
ii. The two coals must blend such that the proportions of each coal add to 1 (unity
condition) and X
1
, X
2
≥ 0.
iii. The chemical requirements and strength requirements in terms of vitrinite
reflectance must be satisfied. A set of points about the origin in the first quadrant of a
rectangular co-ordinate such that the radius, always equal 1, will satisfy conditions 1
and 2 (Fig 1). Therefore:
X
1
= r cos θ
X
2
= r sin θ
By Pathagoras’ theorem, the Cartesian equation representing the locus of point B in the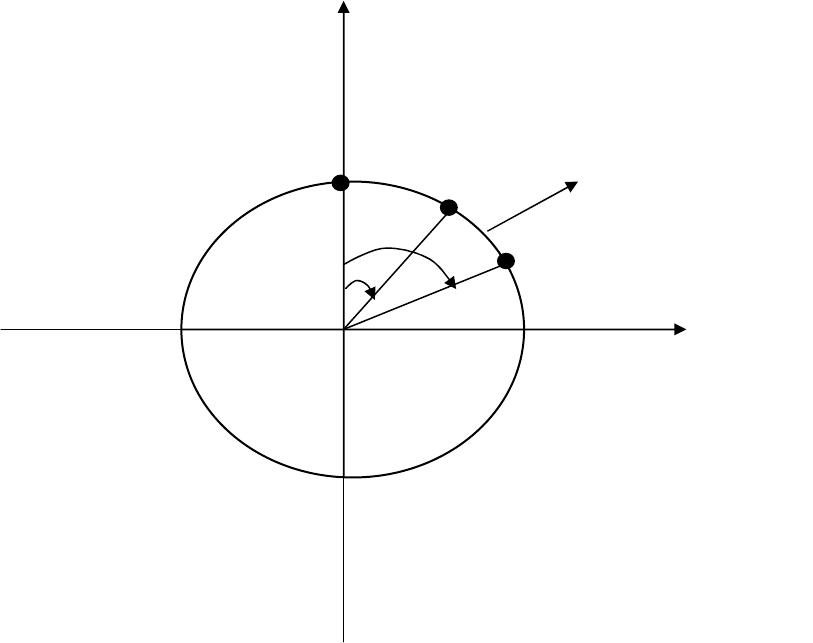

Vol.6, No.2 Numerical Computations to Produce Cokeable Coal Blends 125
X – Y rectangular co-ordinate is obtained as follows:
(r cos θ)
2
+ (r sin θ)
2
= r
2
cos
2
θ + sin
2
θ = 1 (7)
Therefore,
X
1
= cos
2
θ
X
2
= sin
2
θ
mathematically describes the locus of the points which is an arc of a unit radius in the
first quadrant. The third condition will be satisfied by a numerical search of the
interval 0≤θ ≤
л
/
2
on the locus.
Fig. 1: Loci of unit radius in bisection numerical search for optimum θ in binary coal
blending
X
1
X
2
C
B
A
θ
1
θ
2
Search interval

126 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
2.3.2 Ternary Blend
Since a sphere corresponds to a circle in space geometry, a ternary coal blend can be
represented by the spherical co-ordinates (X, Y, Z) [16] such that:
i. A point B is defined by (r, θ, β) where the radius r = 1 unit and
0≤ θ ≤
л
/
2
0 ≤ β ≤
л
/
2
ii. From geometrical analysis, the point B can be represented by the following equations
[16]:
x = r sin θ cos β
y = r sin θ sin β
z = r cos θ
such that r
2
cos
2
θ +r
2
sin
2
θ cos
2
β + r
2
sin
2
θ sin
2
β = r
2
(8)
where
X
1
= proportion of coal 1 in blend = cos
2
θ
X
2
= proportion of coal 2 in blend = sin
2
θ cos2 β
X
3
= proportion of coal 3 in blend = sin
2
θ sin
2
β and
r = 1
The spherical surface bounding the region is the locus of point B.
When β = θ
X
2
= ¼ sin
2
2 θ
X
3
= sin
2
θ sin
2
θ
= sin
4
θ
such that:
0 ≤θ ≤
л
/
2
and 0 ≤β ≤
л
/
2

Vol.6, No.2 Numerical Computations to Produce Cokeable Coal Blends 127
2.3.3 Quaternary Blend
The quaternary blend can be deduced from the binary blend as follows:
(cos
2
θ + sin
2
θ) (cos
2
θ + sin
2
θ) = 1
cos
2
θ cos
2
θ + cos
2
θ sin
2
θ + cos
2
θ sin
2
θ + sin
2
θ sin
2
θ=1
Therefore:
Cos
4
θ + cos
2
θ sin
2
θ + cos
2
θ sin
2
θ + sin
4
θ = 1 (9)
Where:
X
1
= cos
4
θ
X
2
= X
3
= cos
2
θ sin
2
θ
= ¼ sin
2
2 θ
X
4 =
sin
4
θ
such that
0 ≤θ ≤
л
/
2
2.3.4 Higher Blends
Blends of 5 and 6 coals can be similarly deduced from ternary and binary blends and
the resulting equations are:
cos
4
θ+ ¼ sin
2
2 θ+cos
2
θ sin
4
θ + cos
2
θ sin
2
θ+ sin
6
θ =1 (10)
cos
4
θ+cos
4
θ sin
2
θ+cos
2
θ sin
4
θ+cos
2
θ sin
2
θ+cos
2
θ sin
4
θ+ sin
6
θ=1 (11)
for blends with 5 and 6 coals, respectively.
2.4 Direct Search for Optimum
The method of binary division of search interval was used to determine the optimum
cost of the various blends. The basic features are as follows:

128 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
2.4.1 The search Constraints
The search in a direction is reversed for any of the following conditions:
∆R< 0 – vitrinite reflectance constraint
∆A ≥0 – ash content constraint
∆V
L
< 0 - volatile matter constraint (lower limit)
∆V
U
> 0 – volatile matter constraint (upper limit)
∆S ≥ 0 – sulphur content constraint
For the bisection search of a linear solution interval, the absolute error ()r) in the
determination of the solution cannot exceed half the length of the search interval [17], that is:
∆r < 0.5(θ
C
- θ
B
)
where
θ
C =
upper bound of the search interval
θ
B =
lower bound of the search interval
2.4.2 Pseudo-code for the bisection method in coal blending
Step 1: select prime grade coal (X1) such that:
R1> 1.15, A1 <10%, V1 <30.3% ,S1< 0.9%
Step 2: select low -grade coals
Step 3: initialize
Step size, h= 10, X1= 1.0, allowable error (e) = 0.5
0
Evaluate: R, A, S, V,C, ∆R, ∆A, ∆S, ∆V
Counters:m=0,n=0, p=0, q=0
Step 4: IF (∆R >0 AND ∆A<0 AND ∆V
u
<0 AND ∆S<0) THEN
Set:θ= θ + h, m= m + 1
Evaluate: X1, X2…Xn

Vol.6, No.2 Numerical Computations to Produce Cokeable Coal Blends 129
Evaluate: R, A, V, S, ∆R, ∆A, ∆S, ∆V
ELSE
Set: θ= θ + h, n= n + 1
Evaluate: X1, X2…Xn
Evaluate: R,A,S,V,C, ∆R, ∆A, ∆S, ∆V
ENDIF
Step 5: IF(∆R >0 AND ∆A<0 AND ∆V
u
<0 AND ∆S<0 AND∆V
L
>0) THEN
Set: θ= θ + h, p= p + 1
Evaluate: X1, X2…Xn
Evaluate: R, A, V, S, ∆R, ∆A, ∆S, ∆V
ENDIF
Step 6: IF (p>1 AND (∆R ≤ 0 OR∆A≥0 OR ∆V
u
≥0 OR∆S≥0)) THEN
Set: θ= θ + r(h/2
q
), q= q + 1, r = -1
Evaluate: X1, X2…Xn
Evaluate: R, A, V, S, ∆R, ∆A, ∆S, ∆V
ELSE
Set: θ= θ + r(h/2
q
), q= q + 1, r = 1
Evaluate: X1, X2…Xn, Evaluate: R,A,V,S, ∆R, ∆A, ∆S, ∆V
ENDIF
Step 7: IF (∆r<e) STOP

130 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
3.0 RESULTS AND DISCUSSION
3.1 RESULTS
The analytical results of proximate analysis of coals obtained from literature are
presented in Table 1, while the results of some blend calculations are presented in
Tables 2 and 3.
Table 1: Parameters of coal for blending calculations
S/N
Parameters
Ogmore coal
Canada coal
Lafia coal
Okaba coal
1
Avg.
vitrinite
reflectance (R
max
)
1.20
1.52
1.20
0.40
2
Ash (dried basis)
3.40
7.20
26.30
7.32
3
Volatile matter (dried
ash free)
27.40
17.40(db)
32.20
68.78
4
Sulphur (dried basis)
0.20
0.39
2.30
0.66
5
Cost/ ton (US$)
300
300
87.5
34
Table 2: Binary blending of UK Ogmore and Nigerian high ash, high sulphur Lafia coal
θ
q Ogmore Lafia R A V S C
∆
r cv
0 1.0000 0 1.20 3.4 27.40 0.20 300 - V
10 m=1 0.9698 0.0302 1.20 4.09 27.54 0.26 293.58 - V
20 P=1 0.8830 0.1170 1.20 6.08 27.94 0.45 275.14 <5 N
30 P=2 0.750 0.2500 1.20 9.13 28.60 073 246.88 <5 N
40 q=1 0.5868 0.4132 1.20 12.86 29.38 1.07 212.20 A,S
35 q=2 0.6710 0.3299 1.20 10.93 28.98 0.89 230.09 A
32.5 q=3 0.7113 0.2887 1.20 10.01 28.79 0.81 238.65 A
31.25 q=4 0.7309 0.2691 1.20 9.56 28.69 0.77 242.82 <0.63 N
31.875 q=5 0.7211 0.2789 1.20 9.79 28.74 0.79 240.73 <0.32 N
32.1875 q=6 0.7162 0.2838 1.20 9.90 28.76 0.80 239.69 <0.16 N
Note: cv = constraints violated, N= none

Vol.6, No.2 Numerical Computations to Produce Cokeable Coal Blends 131
Table 3: Ternary blending of UK Ogmore, Nigerian Okaba and Lafia coal
θ
q Ogmore Okaba Lafia R A V S C
∆
r c v
0 1.0000 0 0 1.20 3.4 27.40 0.20 300 V
10 p=1 0.9406 0.0009 0.0585 1.20 4.74 27.72 0.32 287.33 N
20 p=2 0.7797 0.0137 0.2066 1.19 8.18 28.96 0.64 252.45 <5 N
30 q=1 0.7660 0.1707 0.0633 1.06 5.52 34.76 0.41 241.14 <5 R,V
25 q=2 0.6747 0.0319 0.2934 1.17 10.24 30.12 0.83 229.19 A
22.5 q=3 0.7286 0.0214 0.2500 1.18 9.21 29.49 0.73 241.18 N
23.75 q=4 0.7019 0.0263 0.2718 1.18 9.73 29.79 0.78 235.25 <0.6
0
N
24.375 q=5 0.6884 0.0290 0.2826 1.18 9.99 29.96 0.81 232.23 <0.31
0
N
Note: cv = constraints violated, N= none
3.2 DISCUSSION OF RESULTS
The ash, volatile matter and sulphur content of 26.30%, 32.20% and 2.30%
respectively, determined for Lafia coal exceeds the upper limits of 10%, 30.3% and
0.9%,respectively, specified for cokemaking at the Ajaokuta Steel Plant [4]. The coking
properties- Gieseler plastometry, crucible swelling number and Ruhr dilatometry are
however not specified for coals to be carbonized at Ajaokuta. Considering the excessive
ash, volatile and sulphur contents of Lafia coal, blend carbonization with low ash and
low sulphur bituminous coals will be necessary.
The numerical blend design gave optimal volatile contents of 28.76%, 29.96%
and 28.85%, respectively, for the proposed binary, ternary and quaternary blends
including Lafia coal. These volatile contents fall within the range specified for
cokemaking at Ajaokuta [4]. For cokemaking in the former Czeckoslovakia, coals with
much lower volatiles of 22.3% had been used [18]. In India, coals with a much lower
volatile of 21.20% had been successfully carbonized to produce coke [19]. For
cokemaking at France’s Usinor plant, coal blends with 24% to 26% volatiles had been
used [20]. Coals with volatiles of 39.4% to 41.8% that far exceed the average volatile
contents of blends including Lafia coal has been reported to produce coke in Japan [21].
In Germany, some lower volatile coals were found to produce coke with lower micum
indices [22]. The three blends obtained for Lafia coal may thus produce coke
on carbonization.
Ash contents of 9.90%, 9.99% and 9.63% determined, respectively for the
proposed binary, ternary and quaternary blends including Lafia coal, falls below the
upper limit of 10% for cokemaking at Ajaokuta [4]. At the France Usinor plant, coals
with lower ash content of 7% to 8% have been carbonized to produce coke [20].
However, in India coals with higher ash content of 17.52% has been successfully used
to produce coke [19]. The three blends proposed including Lafia coal therefore have
acceptable ash contents and may produce metallurgical grade coke on carbonization.
The average sulphur contents of 0.80%, 0.81% and 0.64%, determined
respectively for the proposed binary, ternary and quaternary blends including Lafia coal
fall below the upper limit of 0.9% specified for cokemaking at Ajaokuta [4]. The
sulphur content of 0.27% to 0.38% determined for typical Canadian coal blends are

132 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
lower than the sulphur contents of the proposed blends [10]. However, the sulphur
content of up to 0.95% determined for German Zentral-Kokerei Saar coal blends
exceed 0.81% which is the highest sulphur content for the proposed blends [23]. A low
sulphur content is not an indication of the degree of maturity of coals as shown by the
very low sulphur content of 0.21% determined for the low rank Australian Yallourn
coal [24]. The sulphur contents of the proposed blends thus agree with the international
standard practice for cokemaking and may produce coke with acceptable sulphur
contents.
The average vitrinite reflectance(R
max
) of 1.2, 1.18 and 1.15 determined,
respectively, for the proposed binary, ternary and quaternary blends including Lafia
coal agree with the minimum of 1.15 for coal blends typically in use for carbonization
in the United States of America [8]. The R
max
of 1.28 determined for the Australian
Illawarra coal is higher than 1.18 for the proposed ternary blend [25]. Coal blends with
R
max
of 1.04, which is lower than for the proposed blends have been reported to
produce coke with M10 and M40 of 11.4% and 82.2%, [26]. The Illawarra coal
produced coke with M10 and M40 of 8% and 82%, respectively. On the basis of the
R
max
of the proposed blends, there is a strong indication that the proposed blends will
produce coke with M10 and M40 values that meet the specifications of 9% (maximum)
and 78% (minimum) respectively, for coke to be used in the blast furnace at Ajaokuta
[4].
The inclusion of 28.38%, 28.26%, and 10.81% of Lafia coal in binary, ternary
and quaternary blends were found to produce optimal blends that satisfy the chemical
properties and mechanical strength requirements at the lowest possible estimated costs
of US$239.69, US$ 232.23 and US$ 191.80, respectively; for the three proposed blends
when the average cost of a prime grade coal is taken as US$ 300 per ton [6]. The
proposed blends yield a reduction in cost per ton of cokeable coal of US$ 60.31, US
$67.77 and US$ 108.20 , respectively; in comparison with direct carbonisation of prime
grade coal. Also, 2.90% of non-caking Nigerian Okaba coal was included in ternary
blend.
The 28.38% of Lafia coal proposed for the binary blend agree closely with the
28% determined for bench scale blending of Lafia with 49% UK Ogmore prime coking
coal and 13% non-caking Nigerian Enugu coal [9]. The proposed blends need to be
subjected to bench and pilot scale studies prior to industrial scale cokemaking. A
successful application of these blends at the Ajaokuta steel plant may save about US$
78.40 million, US$ 88.10 million and US$ 140.60 for the proposed binary, ternary and
quaternary blends respectively; on annual importation of 1.3 million tons of prime
coking coal at the completion of Ajaokuta’s first phase. This expected reduction in cost
is significant considering the relatively high cost per ton of US$ 87.50 estimated for
Lafia coal and US$ 34 for the non-caking local coals. The model also ensured that the
excessively high ash and sulphur contents of Lafia coal are not a hindrance to its use in
cokemaking.

Vol.6, No.2 Numerical Computations to Produce Cokeable Coal Blends 133
4.0 CONCLUSIONS
A mathematical model has been elaborated on the basis of analytical geometrical
representation of coal blend components. The model has been applied to propose blends
including up to 28.38% and 29.00% of high ash Nigerian Lafia and non-caking
Nigerian Okaba coals, respectively. The proposed blends will produce significant
reduction in the cost of cokemaking at Ajaokuta when confirmed by bench and pilot
scale carbonization tests
REFERENCES
[1] Poos, A., 1992, “Future requirements for blast furnace coke quality”. Cokemaking
International , vol. 4, 29-30.
[2] Bujnowska, B., and Collin, G., 1992, “Coal tar pitch for improving coking
properties of coal” , In Proc. 2nd International cokemaking congress, London, 1992,
pp. 142-146.
[3] Task Force on the maximum utilization of Nigerian coals at the Ajaokuta steel
plant, 1987, Abuja, Nigeria.
[4] Raw Materials and products specification for Federal Government steel companies,
1994, 1st edn., Abuja, Nigeria.
[5] Moitra A.K., Banerjee, N.G., Shrinkhande K.Y., Sing, K. Raja, K, and Banerjee, S.,
1972 Studies on coal carbonisation in India, 1st edn, Central Fuel Research Institute
Publication, Calculta.
[6] www.englishpeople.com.cn
[7] Adeleke A.O., 1997: Numerical Computations for coal blend optimization, M.Sc
Mathematics Thesis, University of Jos, Nigeria.
[8] Skerl, G.E., 1988, “Automatic coal blend optimisation for cokemaking”. Iron and
steel Engineer, USA, July edn, pp. 39-43.
[9] Ndaji, F.E., Marsh, H.A., 1987, “Laboratory Scale assessment of the utilization
potential of sub-bituminous Nigerian coals as components of coking blends”, Fuel
Processing Technology, Vol. 17, 131-143.
[10] Price, J.T. and Grandsen, J.F., 1987, “Improving coke quality with Canadian
coals”, In Proc. 1st International cokemaking congress, Essen, section E3, preprints
vol.
[11] Panaitescu, C., 1991, Petrographia Carbunilor cocsurilor si producelor Carbonice,
1st edn., Editura Enciclopedia, Bucharest.
[12] Peskett, A.P., 1999 coal Indaba 99, Extract from final proceedings.
[13] Fatunla, S.O ,1993, Fundamentals of FORTRAN programming, 1
st
edn., ADA+
JANE Press,Benin
[14] Hudspeth, M.K., 1983, Introductory Geometry, 1st edn., Addison Wesley, London
[15] Cross, M., and Moscardini, A.O., 1985, Learning the art of Mathematical
modeling, 1st edn., Elis Horwood Ltd, Sussex.
[16] Eckert, E.R.G. and Drake, R.M., 1972, Analysis of heat and mass transfer,
international student edn., McGraw-Hill, London.

134 A.O. ADELEKE and P. ONUMANYI Vol.6, No.2
[17] Curtis, F.G., 1977, Applied Numerical Analysis, 2
nd
edn., Addison-Wesley,
Reading
[18] Buchtele, J., Rozkosny, I and sebestova, E., 1992, “Effect of the organic matter
structure on the coking properties and on the texture formation of model cokes”,In
Proc. 2nd in international cokemaking congress, London, pp. 214 – 230.
[19] Prasad, H.N., Rao P.V.T., Poddar, N.N. and Chaterjee, A., “Selection of coals for
cokemaking by classical top charging and stamp charging”,In Proc. 2
nd
international
cokemaking congress, London, 1992, pp. 231-235.
[21] Katsuhiko, O., Akira, K., Mitsumas, H., Seiji, N. and Kan, A., 1987, “Evaluation
of coking coal”, In Proc. 1
st
International cokemaking congress, Essen, 1987, section
E7.
[22] Weskamp, W., Rhode, W., Stewen, W., and Habermehl, T., 1987, “Greater coke
strength through reactive additives to coking blends”,In Proc. 1
st
International
cokemaking congress, Essen, section II. 1.
[23]Echterhoff, J.,Killich, H.J. and Frick, H.,1992,”Production of blast furnace coke by
stamp charging and utilization of recycled coke breeze”,In Proc. 2
nd
international
cokemaking congress,London,pp172-186
[24] Xiaofeng, X., Akira, O., Tsunenori, N. and Shigeru, M.J., 1998, “Properties and
structure of brown coal treated by hydrothermal process”, 8
th
Australian coal science
conference, NSW, pp. 148.
[25] Broken Hill Proprietary Company (BHP) Publication, 1998, Winning Illawarra
Coal, 8
th
Australian Coal Conference, NSW.
[26] Singh, B.N., Singh B.K., Venugopal, R., Mitra, A.N. and Mukherjee, T., 1987,
“Stamp charging of Indian coals”, In Proc. 1
st
International cokemaking congress,
Essen, section E6.