Journal of Minerals & Materials Characterization & Engineering, Vol. 6, No.2, pp 79-101, 2007
jmmce.org Printed in the USA. All rights reserved
79
SIMULATION STUDIES OF NODULAR IRON’S BULL’S EYE EFFECT ON
STRESS CONCENTRATION UNDER PLANE STRESS CONDITONS
O.O. Oluwole and O.E. Olorunniwo
Materials Science and Engineering Department
Obafemi Awolowo University, Ile-ife, Nigeria
Address for Correspondence: Dr.O.Oluwole, email
Tel. [phone]
Abstract
A simulation study on the effect of the “bull’s eye” in ductile iron on stress
concentrations was done in this work. Using the model of graphite nodules in a cavity, a
two dimensional plate strip was subjected to plane stress conditions. The results were
compared to the traditional theory of modeling the graphite as holes (cavity) in the iron
matrix. In plane stress conditions, while the graphite in the hole model showed the hole
as areas of stress concentration and therefore very critical as regards fracture, the hole
model showed stress concentrated away from the holes making the holes not very
critical factor as regards fracture. It was observed that areas of stress application were
more critical than the voids when using the hole model. Also the graphite in the hole
model was able to predict the good damping behaviour of ductile iron and the increasing
elongation with decreasing nodule count.
Keywords: Simulation, Ductile iron, Bull’s eye, Stress concentration, Plane stress
1.0 Introduction
The high strength of nodular cast iron is well established over grey cast iron
which has flaky distribution of graphite [1,2]. Recent studies have shown the graphite
nodules seated in a cavity in the ductile –iron matrix like a bull’s eye [3]. However, since
graphite is known to have less strength than the ductile iron matrix, it cannot be
considered as a traditional strengthening element like the interstitials or substitutionals. In
gray cast iron, the graphite flakes act as stress raisers, initiating microplastic deformation
at flake tips at low applied stresses. Thus, gray irons cannot exhibit a true elastic
deformation as the plasticity causes the stress-strain curve to decrease continually.
Ferritic ductile irons on the other hand have elongations in the range 18- 30 percent and
tensile strengths equivalent to those of low carbon steel. Pearlitic ductile irons have
tensile strengths exceeding 825MPa but reduced ductility. Austempered ductile iron have

80 O. Oluwole and O. Olorunniwo Vol.6, No.2
strengths exceeding 1600MPa. Thus ductile irons exhibit a proportional stress-strain
relationship similar to steel, but limited by the gradual onset of plastic deformation [4].
Nodularity plays an important part on mechanical properties. Decreasing
nodularity has been seen to decrease tensile, yield and fatigue strengths [4, 5]. Excess
nodule count is also seen to have deleterious effect on mechanical properties.
Previous attempt at modeling ductile cast iron considered the graphite nodules as
holes[6]. However, in the light of recent advances in knowledge in ductile iron
microstructures, it will not be representative to still use the hole as a model for the
graphite nodule.
This paper models the graphite nodules as graphite nodules suspended in a cavity
surrounded by the ductile iron matrix. Comparison is made with the hole model.
2.0 Methodology
2.1 Finite Element Modeling
We consider the material to be isotropic and two dimensional. The material was subjected
to two types of loading: simple tensile loading applied on one side of the plate in the x-
direction, the other sides kept fixed (Fig.a); and also simulation was carried out on a
plate strip subjected to biaxial loading (Fig.b). The Matlab pdetool graphics user interface
was used in the finite element modeling of the material. Three-node triangular elements
were used in meshing and the finite element equation applied to the elements was:
[k
e
]{d
e
} = {f
e
} ………………………………………………(1)
Where
[
]
[ ][][ ] Ω=
∫
Ω
dBDBk
T
e
e
= element stiffness matrix…………….(2)
[B
e
] =


















∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂∂
∂
∂
∂
∂
∂
x
N
y
N
x
N
y
N
x
N
y
N
y
N
y
N
y
N
x
N
x
N
x
N
332211
3
21
3 21
000
000
………………………..(3)
[D] =












−
−
2
1
00
01
01
1
2
ν
ν
ν
ν
E for plane stress condition …………………..(4)

Vol.6, No.2 Simulation Studies of Nodule Iron 81
N
1
, N
2
and N
3
are shape functions for three-node triangular elements.
x and y are the directions in which the forces are acting
E = Youngs modulus of elasticity
ν
= Poisson ratio
{f
e
} = element force vector
{d
e
}= element displacement vector
2.2 Assembly of element equations into global equation and Solving for
displacements
The elemental equations were assembled and solved using the global equation:
[k]\{f} = {d} …………………………………………..……(5)
Where {d} = Nodal displacement vector = {u
1
v
1
u
2
v
2
u
3
v
3
}
T
……..(6)
2.3 Solving for Strains, Stress and Shear stress and strains
Solving for strains, we used the kinematic equation relating strains to displacements
which is stated
as:


















∂
∂
+
∂
∂
∂
∂
∂
∂
=










x
v
y
u
y
v
x
u
xy
y
x
γ
ε
ε
…………………………………………………(7)
Solving for stresses, we used the constitutive equation between stress and strain
{
}
[
]
{
}
εσ D= ……………………………………………………………(8)
For shear stresses, equations of equilibrium of forces acting on two-dimensional
Continuum was used. These are:

82 O. Oluwole and O. Olorunniwo Vol.6, No.2
0=+
∂
∂
+
∂
∂
x
xy
x
f
yx
τ
σ
and
…………………………………………..(9)
0=+
∂
∂
+
∂
∂
y
xyy
f
yx
σ
τ
Where
xyyx
τσσ ,, are stresses acting in the x, y directions and Shear stress, respectively.
3.0 Results And Discussion
Figs.1 and 3 show the stress concentration in the graphite in the cavity model while
Figs.2 and 4 show the stress distribution in the hole model. It could be seen quite clearly
that both show the holes as areas of stress concentrations. However in the direction of
applied stress, the graphite in hole model showed stress concentrations not only at the tips
of the holes but the hole itself is a stress raiser. The y-components of stress was observed
to run across the material for the graphite in the hole model whilst that of the hole model
was localized to the area of stress application and showed high stress values in the y-
direction.This high stress values have translated to high strain (Fig.12) which also
resulted in high shearing strains ( Fig.16). This would consequently result in shear
occurring at point of application of stress. The materials subjected to biaxial loading
(Figs.21-24) showed clearly also that there was severe stress concentration on the bull’s
eye model as opposed to the hole model. The scaling in the biaxial loading showed stress
concentration in the graphite in the hole model to be about three times in the hole model
(Figs. 21-24).
Displacements as a result of same applied stress was observed to be less
pronounced in the graphite in the hole model (Figs.5 and 7) as shown by the scaling of
the displacement contours compared to the hole model (Figs.6 and 8). The hole model
showed about one and a half times more elongation than the graphite in the hole model.
This observation was also corroborated in the materials subjected to biaxial loading (Figs.
17-20). The graphite in the whole model showed that displacement was affected by the
bull’s eye (Figs.5,7,18 and 20) whilst displacement in the hole model followed the
normal flow pattern observed in metals(Figs. 6,8,17 and 19,).I A significant observation
showed the displacements patterns were reflected in the srain patterns . Strains were also
seen to be heavily concentrated on the bull’s eye in the graphite in the hole model
whereas strain was more pronounced at points of applied stress for the hole model
(Figs.9-12 and 25-28).
Shear stresses acting on the graphite in the hole model were observed to be
concentrated at the holes whereas the points of application of stress was the most heavily
stressed part for the hole model (Figs.13 and14). This is even more pronounced under
biaxial stresses (Figs.29 and 30). . This shear stress heavily localized in the hole in which
the graphite sits was observed to be responsible for the shear strains heavily localized in

Vol.6, No.2 Simulation Studies of Nodule Iron 83
the graphite holes as seen in Fig.15 and 32. However in the hole model, under biaxial
loading the model can predict failure by extension of voids,.though strains on the holes
are about half of that in the graphite in hole model.. The implication of this is that
fracture would occur by extension of voids and possible transgranular fracture which
have been observed experimentally in ductile irons[7] . This cannot be predicted by the
hole model for uniaxial loading studied in this work which predicts failure by crack
initiation near the points of applied stress. Thus, graphite in the hole model was seen to
be able to predict very pertinent behaviours in ductile iron which the hole model could
always predict. These are:
(i) The behavior of the bull’s eye tallies with observations of possible fracture
occurring by extension of voids on which graphite nodules[7] which is clearly evident in
this simulation study from the strain concentrations at the holes in which the nodules sit
(Figs.9, 11, 26 and 28).
(ii) The localized non-elastic behavior also noticeable in the stress distributions shows
the good damping property of ductile iron.
(iii) Using a more complex combinations of stresses it was observed that elongation
increased at area of material where nodule count was smaller in the graphite in hole
model and also decreased with increasing nodule count (Figs.18, 19, 33 and 34) which is
consistent with observations in ferritic ductile iron [4].
4.0 Conclusions
Modeling graphite nodules as holes in the ductile iron matrix has been found not to be
able to explain the behavioral pattern noticed experimentally in ductile iron especially
when the material is subjected to biaxial loading and possibly even more complex
loading. The use of graphite in a hole model has been proved to explain the behavior
noticed experimentally in ductile iron such as the damping behavior, increasing
elongation with increasing nodules and possible fracture initiation at voids because of
strain.
References
[1] Walton C.F and Opar T.J. (1981): “Iron casting handbook covering data on Grey,
Malleable and ductile iron, Iron casting Society Inc. New York.
[2] Smith W.F., (1993): “Structure and properties of Engineering alloys”, 2
nd
ed.
McGraw- Hill, New York
[3] Imasogie.B.I and Wendt.U. (2004) “Characterization of Graphite Particle Shape in
Spheroidal Graphite Iron using a Computer-based Image Analyzer”, Journal of Minerals
& Materials Characterization & Engineering, 3(1), 1-12,.
[4] Ductile Iron Society (2006) “Ductile Iron Data for Design Engineers”
http://www.ductile.org/didata/Section3/3part2.htm#Fracture%20Behaviour

84 O. Oluwole and O. Olorunniwo Vol.6, No.2
[5] Janowak.S.F,. Alagarsamy.A and Venugopalan.D (1990) “Fatigue strength of
commercial ductile irons”, AFS Transactions, Vol.98, Pp.511-518.
[6] Pundale. S.H., Rogers.R.J, Nadkarni.G.R (1998) ”Finite Element Modeling of Elastic
Modulus in Ductile Irons: Effect of Graphite Morphology”, Journal of the American
Foundrymen’s Society
98(102), 98-105
[7] Bailey.E (1997) “Transgranular Fracture Surface in Ductile Iron”
( sv.vt.edu/classes/.../97ClassProj/exper/bailey/www/bailey.html)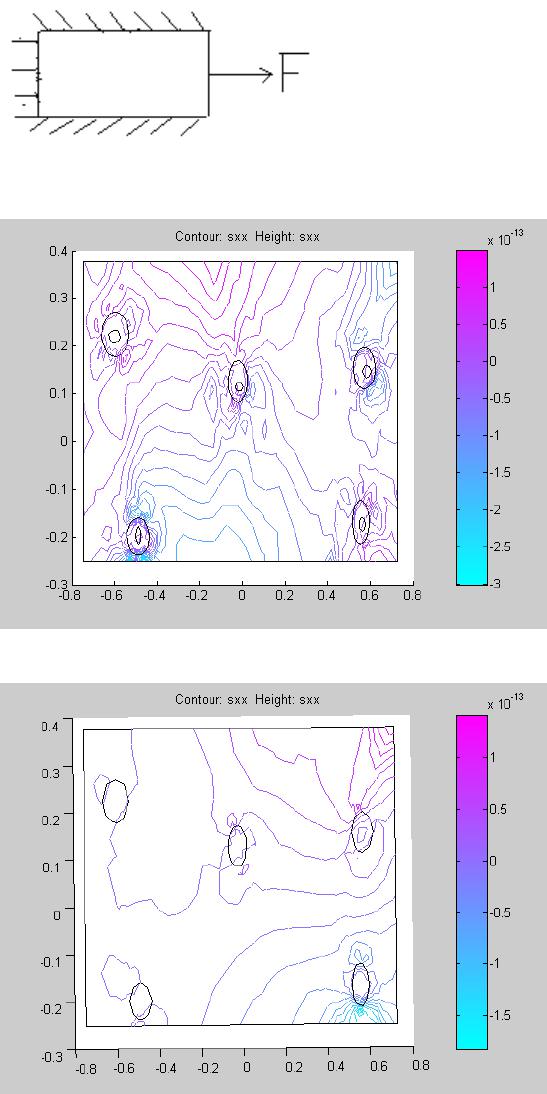

Vol.6, No.2 Simulation Studies of Nodule Iron 85
Figs. 1-16: Results For Uniaxial Loading in X-Direction.
Fig.a: Uniaxial loading;other sides kept fixed.
Fig.1: Stress in x-direction; graphite in hole model
Fig.2: Stress in x-direction; hole model

86 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.3: Stress in y-direction; graphite in hole model
Fig.4: Stress in y-direction; hole model

Vol.6, No.2 Simulation Studies of Nodule Iron 87
Fig.5: Displacement in x-direction; graphite in hole model
Fig.6: Displacement in x-direction; hole model

88 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.7: Displacement in y-direction; graphite in hole model
Fig.8: Displacement in y-direction; hole model.

Vol.6, No.2 Simulation Studies of Nodule Iron 89
Fig.9: Strain in x-direction; graphite in hole model
Fig.10: Strain in x-direction;hole model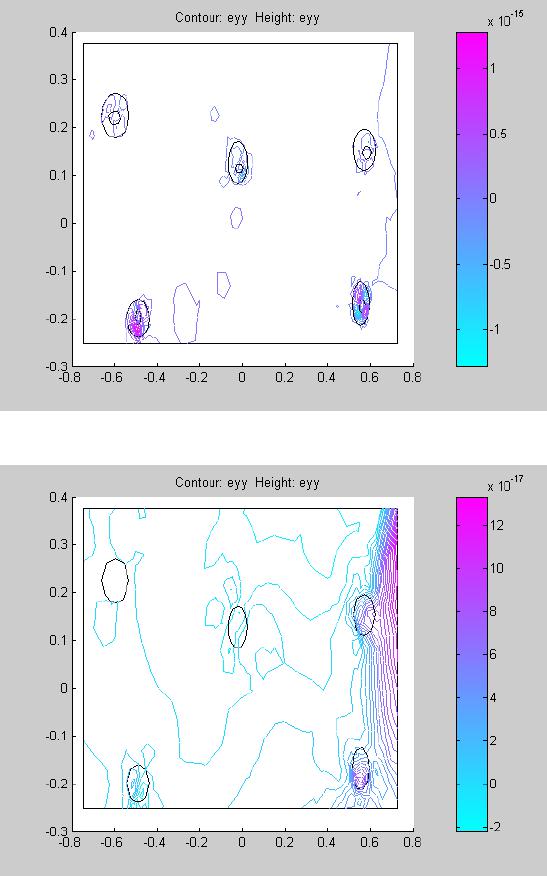

90 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.11: Strain in y-direction; graphite in hole model
Fig.12: Strain in y-direction; hole model

Vol.6, No.2 Simulation Studies of Nodule Iron 91
Fig.13: Shear stress; graphite in hole model
Fig.14: Shear stress, hole model

92 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.15: Shear Strain; graphite in hole model
Fig. 16: Shear strain; hole model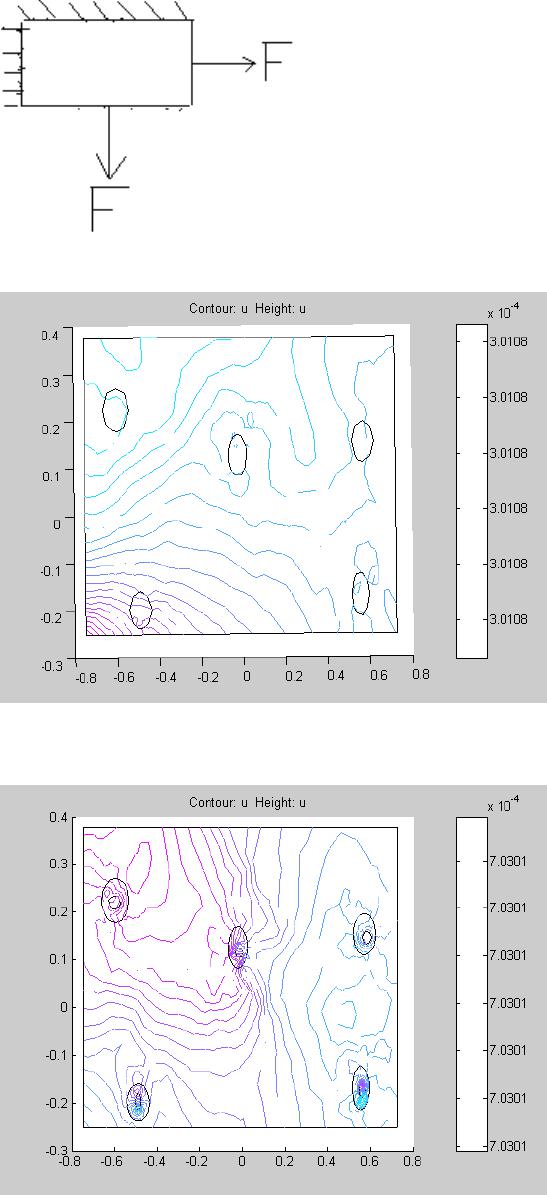

Vol.6, No.2 Simulation Studies of Nodule Iron 93
Figs. 17-32: Results For Biaxial Loading(i.e. in x and y direction)
Fig.b: Biaxial loading; two sides fixed
Fig.17: Displacementin x-direction under biaxial loading; hole model
Fig.18: Displacement in x-direction under biaxial loading; graphite in hole model

94 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.19: Displacements in y direction under biaxial stressing; hole model
Fig.20: Displacements in y direction under biaxial stressing; graphite in hole model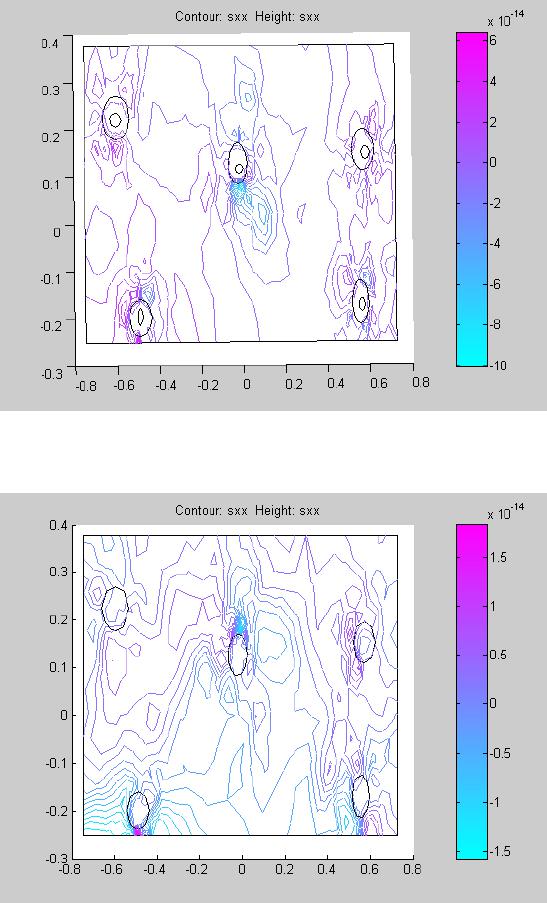

Vol.6, No.2 Simulation Studies of Nodule Iron 95
Fig.21: Stress concentration in x- direction under biaxial loading; graphite in hole model
Fig.22: Stress concentration in x- direction under biaxial loading; hole model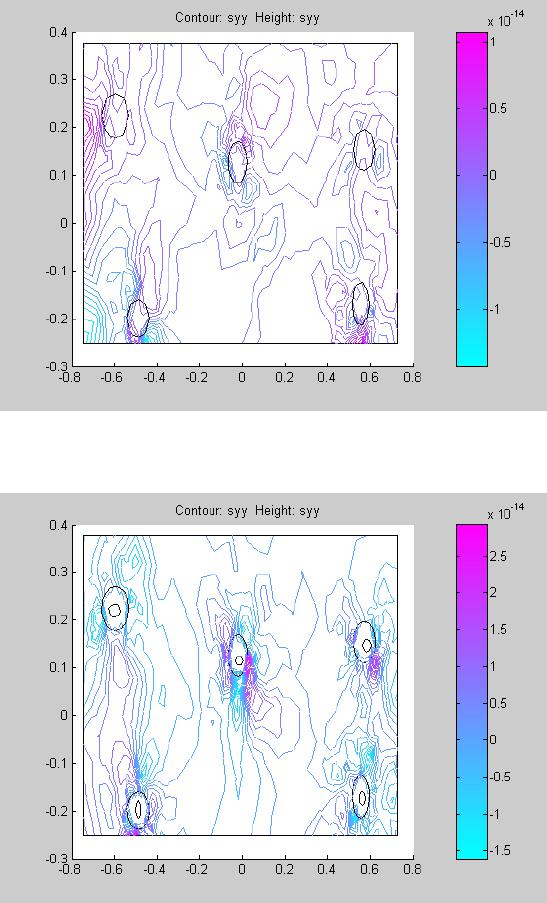

96 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.23: Stress concentration in y- direction under biaxial loading; hole model
Fig.24: Stress concentration in y- direction under biaxial loading; graphite in hole model

Vol.6, No.2 Simulation Studies of Nodule Iron 97
Fig.25: Strain lines in x- direction under biaxial loading; hole model
Fig.26: Strain lines in x- direction under biaxial loading; graphite in hole model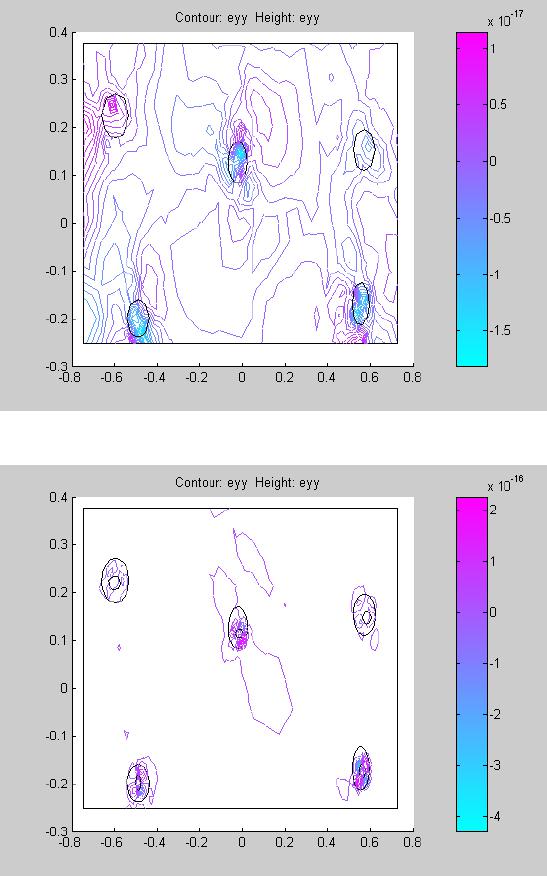

98 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.27: Strain in y- direction under biaxial loading; hole model
Fig.28: Strain in y- direction under biaxial loading; graphite in hole model

Vol.6, No.2 Simulation Studies of Nodule Iron 99
Fig.29: Shear stresses under biaxial loading; hole model
Fig.30: Shear stresses under biaxial loading; graphite in hole model

100 O. Oluwole and O. Olorunniwo Vol.6, No.2
Fig.31: Shear strains under biaxial loading; hole model
Fig.32: Shear strains under biaxial loading; graphite in hole model

Vol.6, No.2 Simulation Studies of Nodule Iron 101
Fig.33: Displacement in x-direction in biaxial loading of material with nodule count of
eleven
showing decrease in elongation as a result of increased nodule count compared toFig.18
Fig.34: Displacement in y-direction in biaxial loading of material with nodule count of
eleven
showing decrease in elongation as a result of increased nodule count compared to Fig.20