Paper Menu >>
Journal Menu >>
 Open Journal of Statistics, 2012, 2, 300-304 http://dx.doi.org/10.4236/ojs.2012.23036 Published Online July 2012 (http://www.SciRP.org/journal/ojs) Multivariate Ratio Estimator of the Population Total under Stratified Random Sampling Oscar O. Ngesa1, George O. Orwa2, Romanus O. Otieno2, Henry M. Murray2 1Ministry of State for Planning, National Development and V2030, Nairobi, Kenya 2Department of Statistics and Actuarial Science, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya Email: oscanges@yahoo.com Received March 7, 2012; revised April 10, 2012; accepted April 30, 2012 ABSTRACT Olkin [1] proposed a ratio estimator considering p auxiliary variables under simple random sampling. As is expected, Simple Random Sampling comes with relatively low levels of precision especially with regard to the fact that its vari- ance is greatest amongst all the sampling schemes. We extend this to stratified random sampling and we consider a case where the strata have varying weights. We have proposed a Multivariate Ratio Estimator for the population mean in the presence of two auxiliary variab les under Stratified Random Sampling with L strata. Based on an empirical study with simulations in R statistical software, the proposed estimator was found to have a smaller bias as compared to Olkin’s estimator. Keywords: Ratio Estimator; Stratification; Auxiliary Variables; Lagrange’s Multiplier 1. Introduction Auxiliary variables have been used to increase precision of estimators especially in reg ression and ratio estimators [2]. This is particularly so in cases of complex surveys, more so in situations where some information on the survey variable might be missing [3]. These classical methods of estimation are based on di- rect estimators, i.e., those which use the response vari- able, y and information provided b y an auxiliary variable, x, highly correlated with the main variable [4]. 2. Review of Multivariate Ratio Estimators Olkin [1] proposed a multivariate generalization of the ratio estimator. Olkin proposed an estimator for the population total, denoted by ˆ M R Y, and defined as 112 2 ˆ 12 M R yy YWXWX pp p y WX xx x 12 12 ˆ ˆ + (2.1) which in other contex t can also be written as; ˆˆ p M RR RpR YWYWY WY (2.2) where ˆi R i i y YX x th i W ˆ is the component of the population total ratio estimate affiliated to the auxiliary variable are the weights which maximize the precision of i M R, subject to a linear constraint 12 p. This estimate of population total also will be accurate if the regression line of Y on 12 Y1W ,,, WW p X XX i is a straight line going through the origin. The population totals for the auxiliary variables X must be explicitly known. 3. The Proposed Estimator Consider a population which has been divided into L strata, with the strata being disjoint, the sample elements from each stratum are sampled and when the measure- ment hi is done, measurement for the unit in the stratum, two auxiliary variables, say, yth i th h1hi x and 2hi x are also measured for that i unit. Let th ˆ M RE ˆ Y denote the proposed multivariable estimator under the stratified random sampling scheme for the population total. M RE Y 1 ˆˆ L is therefore defined as; M RE MRi i YY 11 12 111 12 ˆˆˆ (2.3) where the individual components are defined as follows: M RR R YWYWY 21 22 221 22 ˆˆ ˆR MR R YWYWY 2 1 12 ˆˆ ˆ ··· for the 1st stratum. ··· for the 2nd stratum. R L L MRLLL R YWYWY 2 1 12 ˆˆ ˆ ··· for Lth the stratum. This can further be represented in a single equation as follows; R h h M Rhhh R YWYWY 1, 2,,hL (2.4) are the various strata. where C opyright © 2012 SciRes. OJS  O. O. NGESA ET AL. 301 4. Variance of the Proposed Estimator To compute the values of the weights, the general Equa- tion (2.4) is used and this will cater for each stratum by just changing the value of h in respective strata. Sub- tracting h to the right hand side and left hand side of equation (2.4) yields Y 12 12 ˆˆˆ hh M RhhhR YYWY h Rh WYY 12 1 hh WW 12 = hhhh YWWY 12 ˆˆˆ (2.5) But it is known that the sum of the weights in each stratum is 1, so . This implies that (2.6) Replacing Equation (2.6) to the right hand side of Equation (2.5), yields 12 12 hh M RhhhRhR YYWYWY ˆˆˆ h hh WWY 12 12 12 hh M RhhhRhRh hhh WY WY 12 2 ˆˆˆ hh h YYWYWY Collecting the like terms with respect to weights yields 1MRh hh R hRh YYWYYWYY 112 22 ˆˆˆˆ 2, hhh R R VYW VYWWCovYY 22 122 22 ˆ2 (2.7) Squaring each side and taking Expectation on either side, assuming negligible bias, Equation (2.7) leads to 2 11 22ˆh MRhhRh h hR WV Y (2.8) Equation (2.8) can be written in notation as follows, 11 11 2 M Rhhhhhhh h VYW VWWVWV 1 ˆ Variance h hR VY 2 ˆ Variance h hR VY 12 ˆˆ Covariance , hh hRR VYY W 2h W ˆ (2.9) where 11 22 , and 12 We then proceed to find the values of the weights 1h and that minimize the variance M Rh 1 12 ˆ1h h VYW W VY subject to the linear constraint . 12hh To achieve this, we form a function which has the variance and the linear constraint mentioned above. WW MRh (2.10) with being the Lagrange’s Multiplier. From Equation (2.9), 22 2122 22 ˆ2 11 1 1 M Rhh hhhhhh VYWVWWV WV 22 1 2 21 h h WVWWVWVW W W replacing this into Equation (2.10) yields; 11 112122 22hhhh hh h To minimize this function with respect to the weights 1h and 2h W, we differentiate partially the function with respect to these weights each at a time. 111 212 1 22 hhh h h WV WV W (2.11) 1122 22 2 22 hhhh h WV WV W 111 212 22 hhh h WV WV (2.12) For optimization, we equate the partial derivative Equations (2.11) and (2.12), each to zero. These yields; 1122 22 22 hhhh WV WV (2.13) 1112121122 22 22 22 hhh hhhhh WV WVWVWV (2.14) It follows that Equations (2.13) and (2.14) are equal, then The 2 is common and can be cancelled out. We pro- ceed to collect like terms with respect to the weights and this yield 1 111222212hhhhhh WV VWVV 1WW (2.15) It is known that12hh 21 1 hh , hence WW . From this Equation (2.15) will reduce to 1 111212212 1 hhhhhh WVVW VV and 11112 22122212hhhh hhh WV VVVVV 1h Then it follows, by making W the subject of the formula, 22 12 1 11 122212 hh h hhh h VV WVV VV Opening the brackets in the denominator yields 22 12 11112 22 2 hh hhhh VV WVVV 2h W 21 1 hh WW (2.16) To get the value of weight , we use the linear constraint 22 12 21112 22 12 hh hhhh VV WVVV which may be written as, 11122222 12 21112 221112 22 11 12 21112 22 2 22 2 hhh hh hhhh hhh hh hhhh VVV VV WVVV VVV VV WVVV (2.17) Equations (2.16) and (2.17) give the weights that mini- ˆ mize the variance M Rh VY for stratum h. Copyright © 2012 SciRes. OJS  O. O. NGESA ET AL. Copyright © 2012 SciRes. OJS 302 1, 2,,10i ei y e a b ,andyx x pulation total. The ten strata were again joined together to form one huge stratum, index-wise sample of size 1000 , was selected and then using Olkin’s model, the popula- tion total was estimated. The procedure above was re- peated for 1000 samples and the population totals using each model was recorded. These weights can now be substituted in the proposed model to get the population total. 5. Empirical Study An empirical study was carried out to estimate the popu- lation total of a simulated population and compare the performance of the proposed model to that of Olkin [1]. 8. Simulation Results 6. Description of the Study Population The population total estimates of the two methods were compared to that of the true population (simulated) total. The True population total is 28,235,645. Table 1 sum- marizes the statistics corresponding to each estimator. Figures 1 and 2 show the plotted values of the popula- tion total estimates of proposed model and Olkin’s model, respectively, repeated for 1000 simulations each. In this section we simulated a population (yi, x1i and x2i), which has 10 strata in which each stratum differs from others. This difference was achieved by us- ing different error terms i while generating the us- ing 12iiiiii . The coefficients i and i are randomly generated from a uniform distribution while 12ii i are randomly gene-rated from normal dis- tribution with different para meters. yaxbx ,andx yx In order to show the difference in variability between the two methods, the two plots above are now combined into one graph using a common scale in the Figure 3. 7. Computational Procedure 9. Conclusions A sample of size 300 was selected randomly from the simulated population index-wise, that is if index i is se- lected then the sample elements will have 12ii i . This was repeated for all the ten strata, the selected sam- ple was used in the proposed model to estimate the po- From the summary table above, it can be seen that the proposed estimator gives a total with a very small bias as compared to the Olkin’s. Also, the proposed model can be seen to have a small Root Mean Square Error (RMSE) Table 1. Summary statistics for each method. Min. Median 3rd Qrt Max Mean Bias RMSE Proposed Method 2,821,006 2823185 2,823,565 2823987 2,825,123 2,823,579 144.53 Olkin’s Method 2,746,765 2805085 2,822,892 2840866 2,903,358 2,822,799 7659.34 Figure 1. Plot of the population totals with proposed model for the 1000 samples. 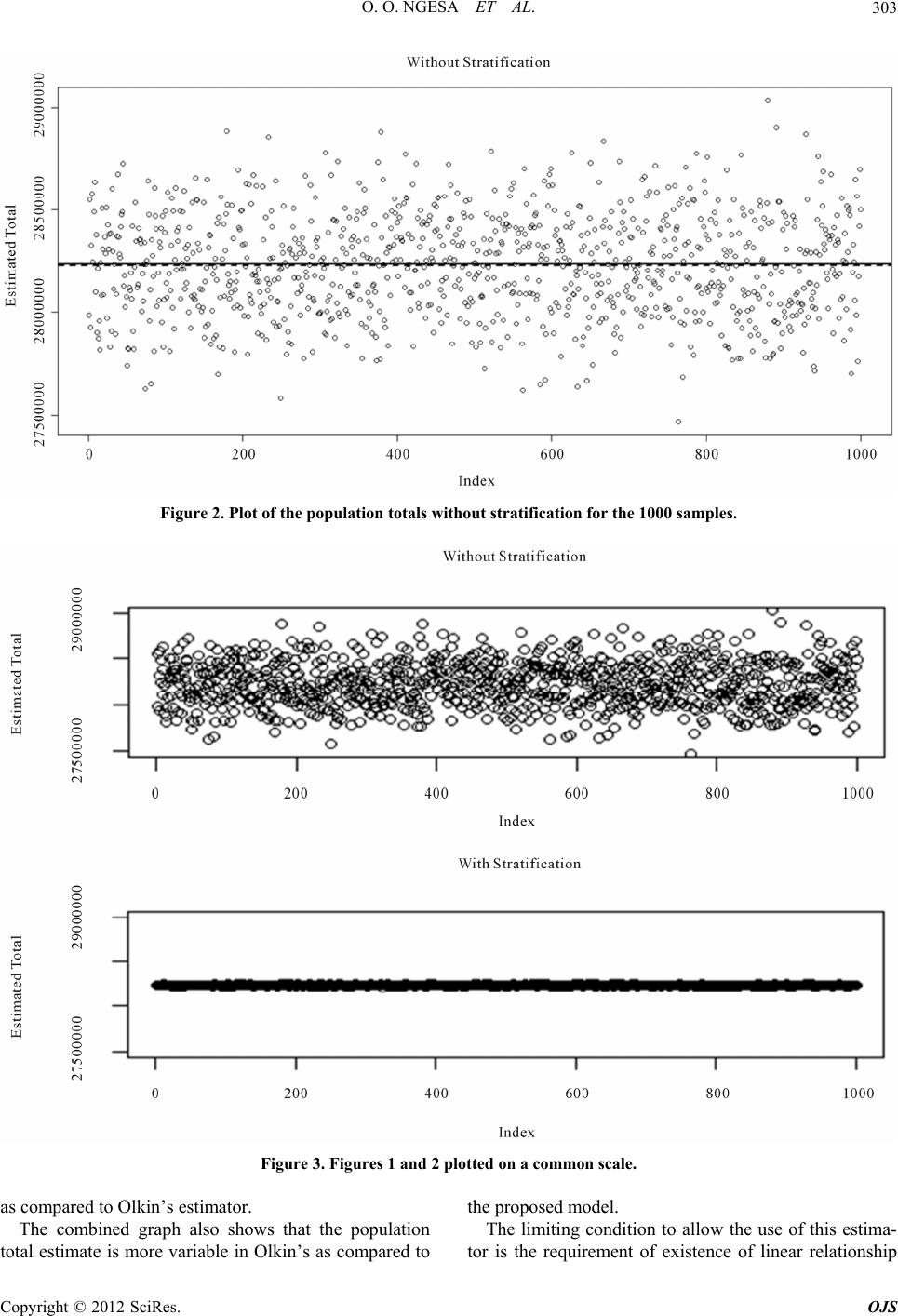 O. O. NGESA ET AL. 303 Figure 2. Plot of the population totals without stratification for the 1000 samples. Figure 3. Figures 1 and 2 plotted on a common scale. as compared to Olkin’s estimator. The combined graph also shows that the population total estimate is more variable in Olkin’s as compared to the proposed model. The limiting condition to allow the use of this estima- tor is the requirement of existence of linear relationship Copyright © 2012 SciRes. OJS  O. O. NGESA ET AL. 304 through the origin between the variable of interest, y, and the auxiliary variables. REFERENCES [1] I. Olkin, “Multivariate Ratio Estimation for Finite Popula- tions,” Biometrika, Vol. 45, No. 1-2, 1956, pp. 154-165. [2] W. G. Cochran , “Sampling Techniques,” 3rd Editio n, Wiley, New York, 1977. [3] L. Y. Deng and R. S. Chikura, “On the Ratio and Regres- sion Estimation in Finite Population Sampling,” Ameri- can Statistician, Vol. 44, No. 4, 1990, pp. 282-284. [4] P. V. Sukhatme and B. V. Sukhatme, “Sampling Theories of Survey with Applications,” Iowa State University Pre ss, Ames, 1970. Copyright © 2012 SciRes. OJS |

