International Journal of Modern Nonlinear Theory and Application, 2012, 1, 33-39
http://dx.doi.org/10.4236/ijmnta.2012.12004 Published Online June 2012 (http://www.SciRP.org/journal/ijmnta) 33
Nonlinear Uncertain HIV-1 Model Controller by Using
Control Lyapunov Function
Fatma A. Alazabi, Mohamed A. Zohdy
Department of Electrical and Computer Engineering, Oakland University, Rochester, USA
Received May 4, 2012; revised May 15 2012; accepted May 25, 2012
ABSTRACT
In this paper, we introduce a new Control Lyapunov Function (CLF) approach for controlling the behavior of nonlinear
uncertain HIV-1 models. The uncertainty is in decay parameters and also external control setting. CLF is then applied to
different strategies. One such strategy considers input into infected cells population stage and the other consid ers input
into a virus population stage. Furthermore, by adding noise to the HIV-1 model a realistic comparison between control
strategies is presented to evaluate the system’s dynamics. It has been demonstrated that nonlinear control has effective-
ness and robustness, in reducing virus loading to an undetectable level.
Keywords: HIV-1 Infection Model; Control Lyapunov Function (CLF); Control Strategy; Uncertain Parameters; Noise
Effect
1. Introduction
Modeling physical or biological phenomena for any dy-
namic system needs to take into account the nature of
connection between the parameters of the dynamic sys-
tem and the observed solution [1]. The function of these
parameters is reflecting the characteristics of studied phe-
nomena such that death rate of productive infected CD 4+T
cells for the HIV model. Therefore, it is valuable to know
about how perturbations in these parameters present the m-
selves in the solution. There are many papers for HIV
modeling that consider the importance of parameters into
a system’s dynamic [2-4]. For example, in [5], a new
mathematical model is pr esented to analyze many details
on HIV-1 viral load data collected from five infected pa-
tients that were administrated using protease inhibitor.
Based on data provided in [5], many viral dynamics that
can not only give the kinetics dynamic of HIV-1 disease
but also give guidelines to develop new treatment strat-
egy are investigated. Controlling HIV infection disease
has been an interesting problem for many researchers
[6-11]. It is well known [12,13] that a control Lyapunov
function, if availab le, will be a conv en ient too l to analyze
stability, evaluate the system's robustness to perturba-
tions, or even to modify the design to enhance robustness
or performance [14]. In this paper, a CLF approach for
nonlinear uncertain HIV-1 model is introduced. The un-
certainty is applied into system’s decay parameters and
external control. Also, two different strategies based on
CLF are investigated. It has been shown that the first
strategy is effective and has an ability to reduce virus
concentration to an undetectable level even under uncer-
tainty and noise effect.
2. Theory of Control Lyapunov Function
(CLF)
A function


Vx is said to be a Lyapunov function for
a given system of vector state equations:


x
Fx
 with ,

00Fn
x
R (1)
If it is class C1 and there exists a neighborhood Q of
the origin such that [15]:


00V

and


0Vx for
x
Q, 0x

(2)






0Vx VxFx


 for
x
Q, 0x

(3)
where:


 


123
,,,..
n
Vx Vx VxVx
Vx xxx x
 


 


 

.
The classical Lyapunov stability theorem states that if
Equation (1) has a suitable Lyapunov function, then the
origin is globally asymptotically stable. Conversely, for
any globally asymptotically s table system (1) with a con-
tinuous right hand side a Lyapunov function class C

can be constructed.
If we consider the control system:

,

x
fxu
 (4)
n
x
R is the state vector. is the control
m
uR
C
opyright © 2012 SciRes. IJMNTA

F. A. ALAZABI, M. A. ZOHDY
34
vector and is assumed continuously be stabilized. Ac-
cording to the above definition, a positive definite C

function exists such th at:


 
inf, 0Vxfxu

 (5)
for each in some neighborhood of the origin.
0xQ
As a result, if the function of class

Vx C

satis-
fies Equations (2) and (5), then it’s called a CLF [15].
3. Selection of Suitable CLF
It was shown in [16] that a first integral for the drift vec-
tor field, plus some controllability conditions can derive
smooth asymptotically stabilizing control laws. This me-
thod has been introduced generally in [15,17], and is
usually called Jurdjevic-Quinn method [14]. The control
strategy based on this requires selection of CLF such that
V(x) is semi-positive definite. Stability is guaranteed if
the derivative of is semi-negative definite. Con-
sidering the following system (linear in control and non-
linear in state):

Vx
 
1
m
oi
ii
x
fx ufx



 (6)
where

o
f
x is a stable unforced system, i is the
designated control, u

th
i
i
f
x is a smooth vector field in
.
n
RWe say that Equation (6) satisfies a Lyapunov condi-
tion of Jurdjevic-Quinn type if there are a neighborhood
of the origin and a function such that
[15]:
Q C

Vx

0Vx for
x
Q, and 0x

00V

(7)




0
o
Vxf x for
x
Q

(8)
Now, the derivative of


Vx with respect to the
closed loop system is given by [15]:

2
10
m
oi
i
VxVxfxVxf x

  


 (9)
According to the Lyapunov control, a control function
is selected as following:
 


ii
ux Vxfx , (10) 1, 2,,im
4. Basic HIV-1 Infection Model
Parameters of HIV-1 infection models were estimated
based on data provided by the Veterans Affairs hospital
in West Haven, Connecticut, for a cohort of 338 people
monitored for up to 2484 days [18]. This basic HIV-1
infection model is bilinear and has three states, namely
uninfected cells


x
, infected cells

y
, and virus


v:
12 3
34
56
x
kkxkxv
ykxvky
vkykv
 





(11)
Let
 
123
,, ,,
TT

x
xxxxyv and let



ddt ,
where

T

denotes transpose, Then:




11 12131
22 31342
33 5263
x
fkk

3
xkx
xf kxxkx
xf kxkx

 
 


x
(12)
Figure 1 shows the dynamic response of HIV-1 in fec-
tion model.
From Equation (12), 1 is the supply rate of unin-
fected cells by the thymus, 2 is the death rate of unin-
fected cells. 3 is the rate of infection, 4 is the death
rate of infected cells, 5 is the rate of virus production
by infected cells, 6 is the clearance rate of the virus.
1
kk
k k
k
k
x
and 2
x
are m easured in (cells/mm3) and 3
x
is meas-
ured in (particles/mm3). Also, from [18] we got Table 1.
5. Robust CLF Controller Design
Many control techniques have been applied for HIV
treatment [19,20], but here we are interested to develop a
new control design based CLF. A stabilizing state feed-
back law can be found via a suitable semi-definite posi-
tive function


Vx in two assumed cases as:
 
121313
313 42
1
52 63
m
oii ii
i
kkxkxx
x
fxufxkxxkxuf x
kx kx




 






(13)
Figure 1. HIV-1 model without CLF, x1(0) = 350, x2(0) =5,
x3(0) =25. 
Table 1. Parameter values used in HIV-1 infection model.
Parameter Value Unit
k1 10 1
31
cells mmy da



k2 0.05 day–1
k3 5 × 10–4 mm3 cells–1·day–1
k4 0.4 day–1
k5 40 day–1
k6 9 day–1

F. A. ALAZABI, M. A. ZOHDY 35
The state feedback law with uncertainty is:
 
123 123
,,,, ,
ii
uxxxVxxx fx 

(14)

Vx from [21] is:

**
**
*
4**
*
5
, ,lnln
ln
*
x
xy
Vxyvxyy
x
xy
kvv
v
kvv



 






y

(15)
Now, we can express as:

,,Vxyv

** 11 22
123 12
** *
11 22
*33 43**
533
,, lnln
ln
*
x
xxx
Vxxxxx
x
xxx
xx kx
kxx












(16)
From we can find :

123
,,Vxxx

123
,,Vxxx

* ** 3
124
123 125
,, 111x
xxk
Vxxxxxkx

 

  

 

3

(17)
where 135
0246
kkk
Rkkk , *1
120
k
xkR ,

*26
20
35
1
kk
xR
kk
,

*2
30
3
1
k
xR
k

From Table 1 we can find and the equilibrium
states: 0
R
010
9
R, , ,
*
1180x* 22.5x* 3100
9
x
5.1. Applying Control Strategy into Infected
Cells with Uncertainty
In this section, we can apply the control input to infected
cells for HIV-1 infection model with uncertainty as:
 


 
1
12 1313
31342162
52 63
,,
0
0
m
oii
i
xfx ufx
kk xkxx
kxxkxu kx
kx kx

 

 







 



(18)
In this case, will be:

1123
,,uxxx



 
1123
* **
43
12 62
125 3
,,
0
11 1
0
uxxx
kx
xx kx
xxk x


   
 

  


 











(19)

*
2
112362 2
,, 1
x
uxxxk x
x

 


5.2. Applying Control Strategy into Virus with
Uncertainty
We can also apply the control input to virus for the HIV-
1 infection model with uncertainty as:
 



1
12 1313
313 421
52 633
,,
0
0
m
oii
i
xfx ufx
kk xkxx
kxx kxu
kx kxx

 

 







 



(21)
In this case,


1123
,,uxxx will be:




1123
* **
43
12
125 3
3
,,
0
11 1
uxxx
kx
xx
xxk x
0
x



 



 

 




 





(22)



*
43
11233 53
,, 1
k
x
uxxx xkx
 
 

 

(23)
6. Noise Effect on HIV-1 Dynamic System
In this section, noise effect on HIV-1 dynamic system
with external control input is investigated into two strate-
gies as:
 

121313
313 42
1
52 63
,
m
oii
i
ii
kkxkxx
xfxufx dkxxkx
kx kx
uf xd




 






 (24)
where represents noise effect. d
7. Simulation and Results
In Figure 2, it is assumed a (±5%) deterministic uncer-
tainty in decay parameters of HIV-1 model are related to
the first strategy. It’s noted that uncertainty doesn’t affect
the control role on reducing viral load to an undetectable
level, however the number of healthy cells with (+5%)
uncertainty is reduced and with (–5%) uncertainty is in-
creased and this can be referred to detrimental and bene-
ficial perturbation respectively.
In Figure 3, it is assumed a high deterministic uncer-
tainty (±20%) in decay parameters of HIV-1 model are
related to the first strategy. It is noted that even for high
uncertainty, the control is still effective on reducing viral
load to an undetectable level, however the number of
healthy cells with (+20%) and (–20%) uncertainty is re-
duced (detrimental perturbation) and increased (benefi-
cial perturbation) respectively.
In Figure 4, it is assumed a (±5%) deterministic un-
certainty in decay parameters of HIV-1 model are related

(20)

F. A. ALAZABI, M. A. ZOHDY
36
Figure 2. Control performance for nonlinear HIV-1 model
under ±5% deterministic parameters uncertainty for first
strategy.
to the second strategy. It's noted that uncertainty affect
the control role on reducing viral concentration to an
undetectable level which means that the first strategy is
more efficient than second strategy.
Figure 3. Control performance for nonlinear HIV-1 model
under ±20% deterministic parameters uncertainty for first
strategy.
In Figure 5 , it is assumed a high (±20%) deterministic
uncertainty in decay parameters of HIV-1 model are re-
lated to the second strategy. It’s noted at high uncertainty,
the control effect becomes worse on reducing viral con-

F. A. ALAZABI, M. A. ZOHDY 37
Figure 4. Control performance for nonlinear HIV-1 model
under ±5% deterministic parameters uncertainty for sec-
ond strategy.
centration.
In Figure 6, we add a constant noise (+10) in HIV-1
model related to first and second strategy. It’s shown that
Figure 5. Control performance for nonlinear HIV-1 mode
and that is also depends on how much noise is added.
d a new robust CLF control de-
l
under ±20% deterministic parameters uncertainty for sec-
ond strategy.
8. Conclusion
noise has a little impact on the HIV-1 system dynamic This paper has presente

F. A. ALAZABI, M. A. ZOHDY
38
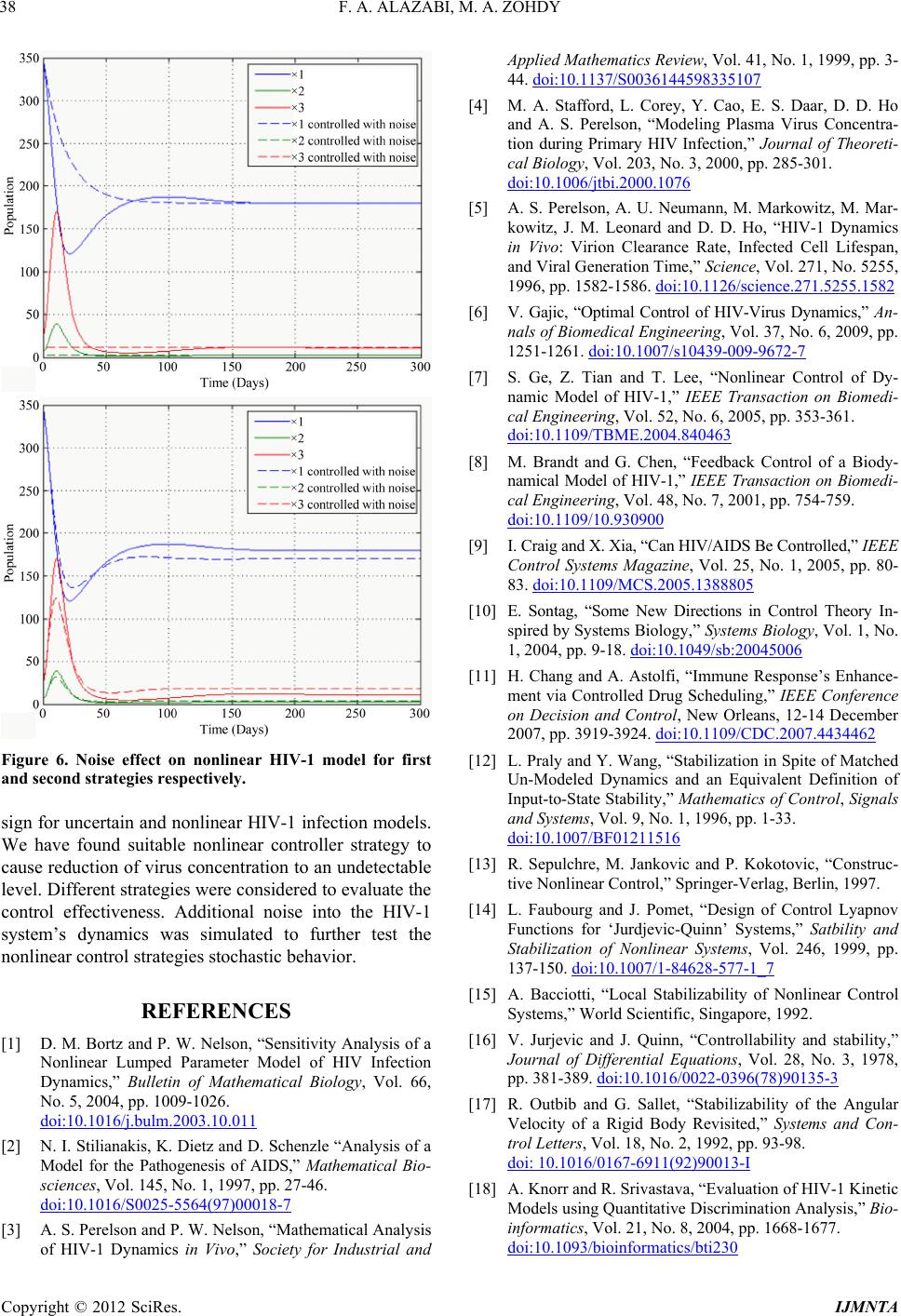
Figure 6. Noise effect on nonlinear HIV-1 model for firs
sign for uncertain and nonlinear HIV-1 infection models.
REFERENCES
[1] D. M. Bortz ativity Analysis of
1
t
and second strategies respectively.
We have found suitable nonlinear controller strategy to
cause reduction of virus concentration to an undetectable
level. Different strategies were considered to evaluate the
control effectiveness. Additional noise into the HIV-1
system’s dynamics was simulated to further test the
nonlinear control strategies stochastic behavior.
nd P. W. Nelson, “Sensi a
Nonlinear Lumped Parameter Model of HIV Infection
Dynamics,” Bulletin of Mathematical Biology, Vol. 66,
No. 5, 2004, pp. 1009-1026.
doi:10.1016/j.bulm.2003.10.01
chenzle “Analysis of a [2] N. I. Stilianakis, K. Dietz and D. S
Model for the Pathogenesis of AIDS,” Mathematical Bio-
sciences, Vol. 145, No. 1, 1997, pp. 27-46.
doi:10.1016/S0025-5564(97)00018-7
[3] A. S. Perelson and P. W. Nelson, “Mathematical Analysis
of HIV-1 Dynamics in Vivo,” Society for Industrial and
Applied Mathematics Review, Vol. 41, No. 1, 1999, pp. 3-
44. doi:10.1137/S0036144598335107
[4] M. A. Stafford, L. Corey, Y. Cao, E. S. Daar, D. D. Ho
and A. S. Perelson, “Modeling Plasma Virus Concentra-
tion during Primary HIV Infection,” Journal of Theoreti-
cal Biology, Vol. 203, No. 3, 2000, pp. 285-301.
doi:10.1006/jtbi.2000.1076
[5] A. S. Perelson, A. U. Neumann, M. Markowitz, M. Mar-
kowitz, J. M. Leonard and D. D. Ho, “HIV-1 Dynamics
in Vivo: Virion Clearance Rate, Infected Cell Lifespan,
and Viral Generation Time,” Science, Vol. 271, No. 5255,
1996, pp. 1582-1586. doi:10.1126/science.271.5255.1582
[6] V. Gajic, “Optimal Control of HIV-Virus Dynamics,” An-
nals of Biomedical Engineering, Vol. 37, No. 6, 2009, pp.
1251-1261. doi:10.1007/s10439-009-9672-7
[7] S. Ge, Z. Tian and T. Lee, “Nonlinear Control of Dy-
namic Model of HIV-1,” IEEE Transaction on Biomedi-
cal Engineering, Vol. 52, No. 6, 2005, pp. 353-361.
doi:10.1109/TBME.2004.840463
[8] M. Brandt and G. Chen, “Feedback Control of a Biody-
namical Model of HIV-1,” IEEE Transaction on Biomedi-
cal Engineering, Vol. 48, No. 7, 2001, pp. 754-759.
doi:10.1109/10.930900
[9] I. Craig and X. Xia, “Can HIV/AIDS Be Controlled,” IEEE
Control Systems Magazine, Vol. 25, No. 1, 2005, pp. 80-
83. doi:10.1109/MCS.2005.1388805
[10] E. Sontag, “Some New Directions in Control Theory In-
spired by Systems Biology,” Systems Biology, Vol. 1, No.
1, 2004, pp. 9-18. doi:10.1049/sb:20045006
[11] H. Chang and A. Astolfi, “Immune Response’s Enhance-
ment via Controlled Drug Scheduling,” IEEE Conference
on Decision and Control, New Orleans, 12-14 December
2007, pp. 3919-3924. doi:10.1109/CDC.2007.4434462
[12] L. Praly and Y. Wang, “Stabilization in Spite of Matched
Un-Modeled Dynamics and an Equivalent Definition of
Input-to-State Stability,” Mathematics of Control, Signals
and Systems, Vol. 9, No. 1, 1996, pp. 1-33.
doi:10.1007/BF01211516
[13] R. Sepulchre, M. Jankovic and P. Kokotovic, “Construc-
v
tive Nonlinear Control,” Springer-Verlag, Berlin, 1997.
[14] L. Faubourg and J. Pomet, “Design of Control Lyapno
Functions for ‘Jurdjevic-Quinn’ Systems,” Satbility and
Stabilization of Nonlinear Systems, Vol. 246, 1999, pp.
137-150. doi:10.1007/1-84628-577-1_7
[15] A. Bacciotti, “Local Stabilizability of Nonlinear Control
stability,”
Systems,” World Scientific, Singapore, 1992.
[16] V. Jurjevic and J. Quinn, “Controllability and
Journal of Differential Equations, Vol. 28, No. 3, 1978,
pp. 381-389. doi:10.1016/0022-0396(78)90135-3
[17] R. Outbib and G. Sallet, “Stabilizability of the Angular
Velocity of a Rigid Body Revisited,” Systems and Con-
trol Letters, Vol. 18, No. 2, 1992, pp. 93-98.
doi: 10.1016/0167-6911(92)90013-I
[18] A. Knorr and R. Srivastava, “Evaluation of HIV-1 Kinetic
Models using Quantitative Discrimination Analysis,” Bio-
informatics, Vol. 21, No. 8, 2004, pp. 1668-1677.
doi:10.1093/bioinformatics/bti230

F. A. ALAZABI, M. A. ZOHDY
39
Optimal Impulse Con- [19] V. Yadav and S. N. Balakris hnan, “
trol of Systems with Control Constraints and Application
to HIV Treatment,” Proceedings of the 2006 American
Control Conference, Minneapolis, 14-16 June 2006, pp.
4824-4829. doi.org/10.1109/ACC.2006.1657484
[20] R. Zurakowski and A. R. Teel, “Enhancing Immune Re-
sponse to HIV Infection Using MPC-Based Treatment
Scheduling,” Proceedings of the 2003 American Control
Conference, Denver, 4-6 June 2003, pp. 1182-1187.
doi:10.1109/ACC.2003.1239748
[21] A. Korobeinikov, “Global Properties of Basic Virus Dy-
namics Models,” Bulletin of Mathematical Biology, Vol.
66, No. 4, 2004, pp. 879-883.
doi:10.1016/j.bulm.2004.02.001