Journal of Minerals & Materials Characterization & Engineering, Vol. 5, No.1, pp 73-86, 2006
jmmce.org
Printed in the USA. All rights reserved
Surface Area and Conductivity of Open-Cell Carbon Foams
Adriana M. Druma, M. Khairul Alam*, Calin Druma
Department of Mechanical Engineering, Ohio University
Athens, OH 45701
*Correspondence Author’s Email:
Abstract
High thermal conductivity carbon foams have recently emerged as an effective
thermal management material for space applications due to their lightweight. Open cell
carbon foams are generally processed from pitch material obtained from coal or
petroleum. These foams have spherical pores that create a three dimensional network of
ligaments and nodes of complex geometry. The thermal conductivity of carbon foams can
be studied numerically by finite element method; however the analysis requires a very
fine grid that captures the microstructure of the foam. In this work, an analytical model
for surface area and thermal conductivity is developed for a foam. To reduce the
computational effort, an electrical circuit network analogy is used to calculate the bulk
thermal conductivity of the foam. The analytical solution is then compared with semi-
empirical models, FEM solution and other analytical solutions.
Nomenclature
A
total cross-sectional area of the unit cell [m
2
];
g
A
cross-sectional area of the gas phase in the unit cell [m
2
];
s
A cross-sectional area of the solid phase in the unit cell [m
2
];
K
e
effective thermal conductivity [W/mK];
K
g
gas thermal conductivity [W/mK];
K
s
solid thermal conductivity [W/mK];
K
sj
solid thermal conductivity (at the juncture or nodes) [W/mK];
K
sl
solid thermal conductivity in the ligaments (longitudinal direction) [W/mK];
K
st
solid thermal conductivity in the ligaments (transversal direction) [W/mK];
P porosity [%];
R
p
radius of the pores [m];
t
Ris the thermal resistance of the foam [°C/W].
D
p
pore diameter [m];
F is the solid conduction efficiency factor [-];
V
p
pore volume [m
3
];
V
lens
lens volume [m
3
];
X, Y, Z coordinate system axes [-];
P
1
, P
2
pore intersection points [-];
h height [m];
d distance between two spheres [m];
2a unit cell size [m];
73

74 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
r
z
in-plane pore radius [m];
t normalized thickness [-];
x integration parameter [m];
z heat flux direction [m];
ϕ Fraction defined in Eq. 6.
Introduction
Carbon foams are cellular structures that consist of randomly distributed spherical
pores. The size of the pores of a typical carbon foam is 100 to 500 microns. Due to its
complex structure of three-dimensional interconnected pores, carbon foams are very
difficult to model analytically. Several researchers studied the effective conductivity of
foams. Calmidi [1998] considered the structure of the metal foam to be made of
dodecahedron-like cells with 12-14 pentagonal or hexagonal faces. The edges of the cells
are formed by individual ligaments and it is considered that there is a lumping of material
(intersection) at intersection points of the ligaments. This approach was successfully used
by Kunny [1960], Zehner [1970], Hsu [1994], and Hsu [1995] to study the effective
thermal conductivity of packed beds.
Fu et al [1998] developed an analytical model to determine the effective thermal
conductivity of cellular ceramics. Two unit cells were developed to predict the effective
thermal conductivity of porous materials using the electrical-circuit analogy. The first
unit cell was a cubic-shaped box. The second unit cell was a cube with a pore in the
center.
Tee et al. [1999] studied the thermal conductivity of carbon foam using a
geometrical model that consisted of a unit cell made up of twelve struts with square
cross-sectional area and eight cubic strut junctures. Tee et al. also used the analogy
between thermal and electric resistors and simulated the unit cell by using series and
parallel combinations of resistors.
Bhattacharya et al. [2002] studied the thermophysical properties of high porosity
metal foams. For their study they considered a model consisting of a two-dimensional
array of hexagonal cells where the struts form the sides of the hexagons. The junction
was taken into account by considering a circular junction of metal at the intersection of
the struts. This study showed that the effective thermal conductivity depends strongly on
the porosity and the ratio of the cross-sections of the fiber and the intersection.
Balantrapu et al [2005] investigated the specific surface and effective thermal
conductivity of open-cell lattice structure consisting of mutually orthogonal cylindrical
ligaments used in heat exchanger applications.
This paper is based on an analytical solution for total surface area and thermal
conductivity of a foam that has spherical pores [Druma, 2005]. With the approximation
of local one-dimensional heat flow, it is possible to determine the thermal resistance of
the bulk foam by adding the local thermal resistances. The specific surface area of the
foam per unit volume is dependent on the porosity and pore size and distribution in the
foam. In this study, the surface area for a foam with 100 micron pores is calculated and
compared to the results given by a commercial solid modeling software package.

Vol.5, No.1 Surface area and conductivity of open-cell carbon foams 75
Theory
Fu et al. [1998] used a representative cubic unit cell to determine an expression
for the effective thermal conductivity. In this study two models are examined; the first is
the simple cubic model with a hollow sphere in the center of a cube. The second model
consists of a rectangular-shaped unit box (cubic) with the transverse section of the solid
beams that enclose the unit cells being squares with normalized thickness t. Using the
electrical-circuit analogy, the effective thermal conductivity of the second model can be
expressed as (Fu et al. [1998]):
()
()
() []
()
()
()
1
2222
41/4
21
211/21
2
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−+
−
+
−−+−
=
tKKt
t
tKKt
t
K
K
gs
gs
g
e
(1)
To use Eq. (1) above, only one geometrical parameter is needed and that is the
normalized thickness of the strand or ligament, t. This thickness can be determined by
knowing the porosity of the foam and it is given by the following equation (Fu et al.
[1998]):
()()
100
21621
23
P
ttt=−+−
(2)
Tee at al. [1999] used a similar model to study the effect of anisotropy of the
carbon foam struts on the bulk thermal conductivity of the foam. The effective thermal
conductivity, , was calculated to be:
e
K
()
()
(
)
(
)
tKtK
ttKK
tKtK
tKK
tKK
stg
gst
sjsl
sjsl
ge
−+
−
+
−+
+−=
1
12
1
1
2
2
(3)
where
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−+=
−
π
3
4
1
100
2
cos
3
1
cos
2
1
1
P
t (3a)
are the thermal conductivities of the struts’ longitudinal direction and of
the juncture respectively [W/mK].
sjsl
KK,
In the hollow-sphere-in-cube model developed by Fu et al. [1998], the porosity is
given by the following:
100
8
1
2
3
3
4
2
23
×
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
pp
RRP π (4)
The above model is valid for porosity between 52% and 96%. The bulk thermal
conductivity of the foam is then calculated with the following equation (Fu et al. [1998]):
()
()
1
0
2
1
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
=
∫
a
dx
KAAKAA
K
b
ggss
b
(5)
Based on the approach used by Bhattacharya et al. [2002], where the thermal
conductivity is the square root of the sum of the squares of the parallel and series

76 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
arrangements, Sullins et al. [2001] found the effective thermal conductivity as a function
of thermal conductivity of the gas () and material of the foam () to be:
g
K
s
K
() [] ()
()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅−+⋅⋅
⋅⋅
⋅−+⋅⋅−+⋅=
gs
gs
sge
KPKFP
KKF
KFPKPK
1
11
ϕϕ
(6)
where:
ϕ
is the fraction of heat transfer in parallel mode and (1-
ϕ
) is the fraction of heat
transfer in series mode.
In Eq. (6) the solid conduction efficiency factor (F) accounts for the tortuous path
for conduction through the cell walls.
Most of the above approaches are not applicable for the carbon foam geometry
because the foam does not have well defined struts. Several authors, including Bauer
[1993], have presented semi-analytical approaches using a ‘pore conduction’ factor that
must be evaluated experimentally.
The present work modifies Fu’s approach to develop an analytical model for the
thermal conductivity of a foam with spherical pores that may be closed pores or
interconnected (overlapping) pores. In this approach, the local thermal resistances are
summed up, or integrated to determine the resistance of the bulk foam. The focus of this
study is to develop analytical solutions for total surface area and thermal conductivity of
carbon foams based on unit cells, where the pores are distributed in a body centered cubic
cell pattern. Such a unit cell is more representative of carbon foams than the cubic
structure built of straight beams that has been used by Tee et al. [1999].
Determination of Surface area of the foam
The surface area of the foams is of particular interest in heat transfer applications
where the main heat removal mechanism is convection. The open cell foams are therefore
the main interest of this study. The foam will be modeled with pores arranged in a body
centered cubic (BCC) cell distribution. In this model, the open cell foams have open cells
(interconnected porosity) when the porosity P is greater than 68% (). Above this
porosity the pores having the diameter,
%68>P
2
32a
D
p
<
, become interconnected.
The approach follows the mathematical model developed by Druma [2005] by
considering a coordinate system with the OX axis oriented in the direction of the main
diagonal of the unit cell cube and the origin in the center point of the middle sphere (as
shown in Fig.1). The equations of the two spherical pores (center and corner pore) can be
written as (Druma [2005]):
()
222
2
2222
p
p
RZYdX
RZYX
=++−
=++
(7.a)
where
2
32a
d=
is the distance between the two spheres (half diagonal of the unit cell).

Vol.5, No.1 Surface area and conductivity of open-cell carbon foams 77
X (unit cell’s diagonal direction)
Y
Z
Corner pore
Center pore
2a
O
Figure 1: Spatial representation of the Ox axis and pore intersection (Druma [2005])
Combining the two equations yields:
2
d
X=
(7.b)
Equation (7.a) shows that the “spherical pores intersect at the mid-distance between the
two centers and the intersection curve has the equation Æ
2222
XRZY
p
−=+
4
2
222
d
RZY
p
−=+which is a circle in the plane perpendicular on the main diagonal of
the cubical cell and with the radius
4
2
2
d
Rr
pi
−=” (Druma [2005]) as shown in Fig. 2.
X
h
R
p
==
d
R
p
Figure 2: Planar section of the pores intersection (Druma [2005])

78 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
It can be concluded that the intersection of the two pores is a “three-dimensional
lens” and its volume can be found by adding the volumes of the two spherical caps
forming the lens.
For the open-cell foams, the void volume can be calculated with the following (Druma
[2005]):
lens
p
p
V
R
V8
3
8
3
−=
π
(8)
where
()
hR
h
V
plens
−=3
3
2
2
π
(9)
with
2
d
Rh
p
−=
is the height of the intersection lens [m]
Therefore
()
(
2
24
12
dRdRV
plens
−+=
)
π
and the porous volume yields:
(
332
1212
3
2
dRdRV
ppp
−−= )
π
(10)
The porosity of the unit cell is therefore:
()
100
8
1212
3
2
3
332
×
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−−
=
a
dRdR
P
pp
π
(11)
Replacing
2
32a
d=
into Eq. 11 and rearranging the resulting equation yields:
032
1004
3
8
323
=+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
pp
DaD
P
a ππ
π
(12)
Equation 12 can be used to find the size of the unit cell for a given porosity and
pore diameter.
The constraint imposed to the solution is:
3
2
2
p
p
D
aD<≤
(13)
The restriction formulated by Eq.13 can be translated as:
94.068.0<<P
(14)
The equation can be solved numerically yielding a solution that satisfies the
geometrical constrain given by Eq. 13.
Total surface area of the foam (open cell)
lenspp
SRS88
2
−= π
(15)
Total surface area of the lens is given by
⎟
⎠
⎞
⎜
⎝
⎛
−==
−
+−==
∫
−
2
44142
22
2
22
d
RRhRdx
xR
x
xRSS
ppp
R
hR
p
pcaplens
πππ
(16)

Vol.5, No.1 Surface area and conductivity of open-cell carbon foams 79
Replacing Eq. 16 and
2
32a
d=
into Eq. 15, the total area of the unit cell (open cell
foams) can be written as:
(
)
[
]
[
]
ppppppppp
DaDaDDD
d
RRRS334232222
2
328
2
−=−−=
⎟
⎠
⎞
⎜
⎝
⎛
−−=
ππππ
(17)
For open cell foams with porosity above 94%, the diameter of the center pore
becomes larger than the unit cell and the size of the unit cell can be calculated with the
following equation:
021
2
3
32
10024
3
8
323
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++
pp
DaD
P
a ππ
ππ
(18)
with the constraint that
2
23
2
a
Da
p
<<
for structural integrity.
Total surface area of the unit cell, for open cell foams, with porosity above 94%
can be calculated with the following formula:
() []
()
(
)
[
]
ppp
p
pppp
DaDaD
D
aDDDS6233222
2
12342−+=−−−−= π
π
π (19)
The results for 100 microns pore diameter and different porosities are presented in Table
1 and compared with results from a solid modeling software program (Solid Edge).
Table 1: Surface areas (unit cell) for open and closed cell foams
Surface area [mm
2
] Percentage
Difference Porosity
[%]
Analytical Software
(Solid Edge) [%]
70 0.06039 0.06029 0.166
75 0.05421 0.05419 0.037
80 0.04795 0.04793 0.042
85 0.04153 0.04156 0.072
90 0.03482 0.03485 0.086
95 0.0261 0.02614 0.153
Table 1 shows that the surface area calculated with the analytical formulas
derived above matches very well with the solid modeling software prediction (difference
below 0.2% between the solid modeling software and analytical result). The formulas
developed above can therefore be used to estimate the surface area for open- cell cellular
foams.
Determination of bulk thermal conductivity
Based on the body cubic centered unit cell presented in Fig. 3 below, an analytical
model has been developed to predict the thermal conductivity of the foam. The model is
based on the thermal resistance formula (Fu et. al. [1998]) using the analogy between
thermal and electrical resistance. In this model, thermal resistances for differential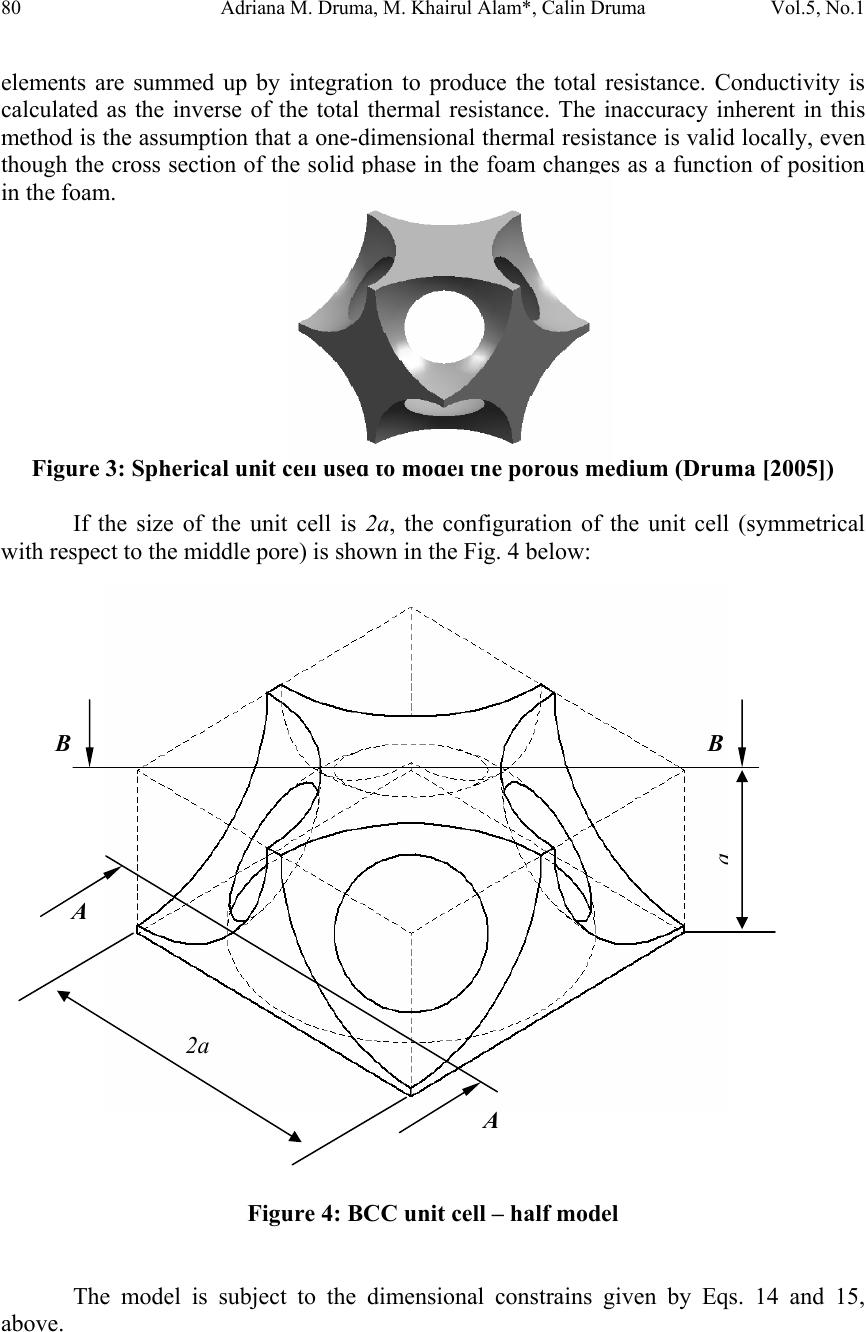

80 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
elements are summed up by integration to produce the total resistance. Conductivity is
calculated as the inverse of the total thermal resistance. The inaccuracy inherent in this
method is the assumption that a one-dimensional thermal resistance is valid locally, even
though the cross section of the solid phase in the foam changes as a function of position
in the foam.
Figure 3: Spherical unit cell used to model the porous medium (Druma [2005])
If the size of the unit cell is 2a, the configuration of the unit cell (symmetrical
with respect to the middle pore) is shown in the Fig. 4 below:
a
2a
A
A
B B
Figure 4: BCC unit cell – half model
The model is subject to the dimensional constrains given by Eqs. 14 and 15,
above.

Vol.5, No.1 Surface area and conductivity of open-cell carbon foams 81
From Fig. 4, it can be seen that the intersection between the center pore and the
corner pores is circular, situated in a plane perpendicular to the diagonal of the unit cell
as shown below (see Fig. 5).
a
R
p
P
1
P
2
R
p
Figure 5: Section B-B (quarter of the diagonal plane)
22a
z
z
R
p
5
4
3
2
1
The two points where the pores become interconnected (P
1
and P
2
in Fig. 5) are
situated at the heights:
23
2
2
2
2
1
a
R
a
z
p
−−=
(20)
23
2
2
2
2
2
a
R
a
z
p
−+=
(21)
For open cell foams (BCC case), the size of the unit cell can be calculated with
the formula given by Eq. 12.
The local radiuses of the circular pore surfaces containing the cross-section (B-B)
can be calculated with the formulas:
Center pore:
22
zRr
z
−= (22)
Corner pore:
()
2
2'
zaRr
z
−−=
(23)
where z is the vertical coordinate measured from the center of the middle pore [m].
Table 2 below contains the cross-section perpendicular to the axis of interest for
calculating the effective thermal conductivity at different points in the unit cell as shown
in Fig. 5. As the pore configuration changes, so does the planar cross-section. However,
the total cross section area is constant:.
2
4aA =

82 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
Table 2: Cross-sections through the unit cell and void area (Druma, [2005]).
No A-A Cross-section
A
p
A
s
z
1
(
)
22
zR− π
[0, a-
R)
2
(
)
[
]
{
}
2
22
2zazR−+− π
[a-R,
z
1
)
3
(
)
[
]
(
)
()
()
() []
()
()
[]
()
()
⎭
⎬
⎫
⎩
⎨
⎧
−
⎥
⎦
⎤
⎢
⎣
⎡
−−+−
⋅
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
−−−−−
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−
+−−
⋅−−
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−−+
⋅−+−−−
2
2
2
222
2
2
2222
2
2
2
2
2
2
2
22
2
2
2
22
2
22
2
2
2
22
2
cos
4
22
2
cos
42
azaRzR
zaRzRa
zaRa
zzaa
a
zaR
zRa
zzaa
a
zRzazR π
[z
1
, z
2
]
4
(
)
[
]
{
}
2
22
2zazR−+− π
4a
2
-
A
p
(z
2
, R]

Vol.5, No.1 Surface area and conductivity of open-cell carbon foams 83
5
(
)
[
]
2
2
zaR−− π
(R, a]
Using the definition of the thermal resistance, the bulk thermal conductivity can
be calculated from the following formula:
AR
a
K
t
b
=
(24)
For a finite increment dz along the vertical axis, the thermal resistance dR
t
is:
ggss
t
KAKA
dz
dR
+
=
(25)
Integrating the equation above between 0 and a, and replacing the thermal
resistance in Eq. 24 yields the bulk thermal conductivity:
∫
+
==
a
ggss
t
b
a
dz
KAKA
A
AR
a
K
0
1
(26)
For foams, the thermal conductivity of the pore’s content (gas) is much lower than
the solid thermal conductivity and can therefore be approximated to zero. In this case, the
formula above becomes:
∫
==
a
ss
t
b
a
dz
KA
A
AR
a
K
0
1
(27)
The effective thermal conductivity of the foam with constant solid thermal
conductivity can therefore be calculated as follows:
∫
==
a
s
s
b
e
a
dz
A
A
K
K
K
0
1
(28)
The integral in Eq. 28 does not have an analytical solution and is calculated
numerically using an adaptive quadrature and the results are presented in Table 3
[Druma, 2005] below. Table 3 also shows the comparison between the finite element
(FEM) calculation carried out [Druma et al., 2004] by using a commercial software

84 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
program (ALGOR), and the semi-analytical model developed by Bauer [1993]. Bauer
developed a semi-analytical approach to obtain the following equation:
n
s
b
e
P
K
K
K
/1
100
1
⎟
⎠
⎞
⎜
⎝
⎛
−==
(29)
where ‘n’ is an unknown parameter, usually termed the ‘pore conduction factor’. A value
of ‘n=0.77’ provides a good fit to some of the experimental data analyzed by Bauer, and
is also comparable to numerical results [Druma et al., 2004]. It can be observed that the
analytical model overpredicts the thermal conductivity; this is to be expected since the
analytical model does not take the tortuosity of the heat transfer path into account.
Table 3: Effective Thermal Conductivity: Analytical - FEM comparison
K
e
No.
Porosity
[%]
2a
[mm]
Analytical
Model
FEM
Bauer
Model
1 70 0.114 0.27 0.251 0.21
2 75 0.111 0.213 0.197 0.165
3 80 0.108 0.159 0.147 0.124
4 85 0.105 0.111 0.1 0.085
5 90 0.102 0.077 0.067 0.05
However, the analytical model matches the FEM results better than the Bauer
model, and this can be seen in Figure 6. The comparison between the FEM and anaytical
model is also shown in Fig. 6, along with Bauer model (Bauer [1993]), Cubic model (Fu
et.al. [1998]), and Hollow-Sphere-in-Cube Model (Fu et.al. [1998]) . It should be noted
that the pore diameter is kept constant at 100 micrometers for all porosities. Therefore, as
the porosity increases, the distance between pores becomes smaller. In other words, the
variable porosity at constant pore size causes the change in the size of the unit cell. The
rule of mixtures assumes a linear relationship with the contribution of each phase
according to volume fractions and provides the highest estimate of the conductivity
value; it is equivalent to using ϕ=0 in Eq. 6.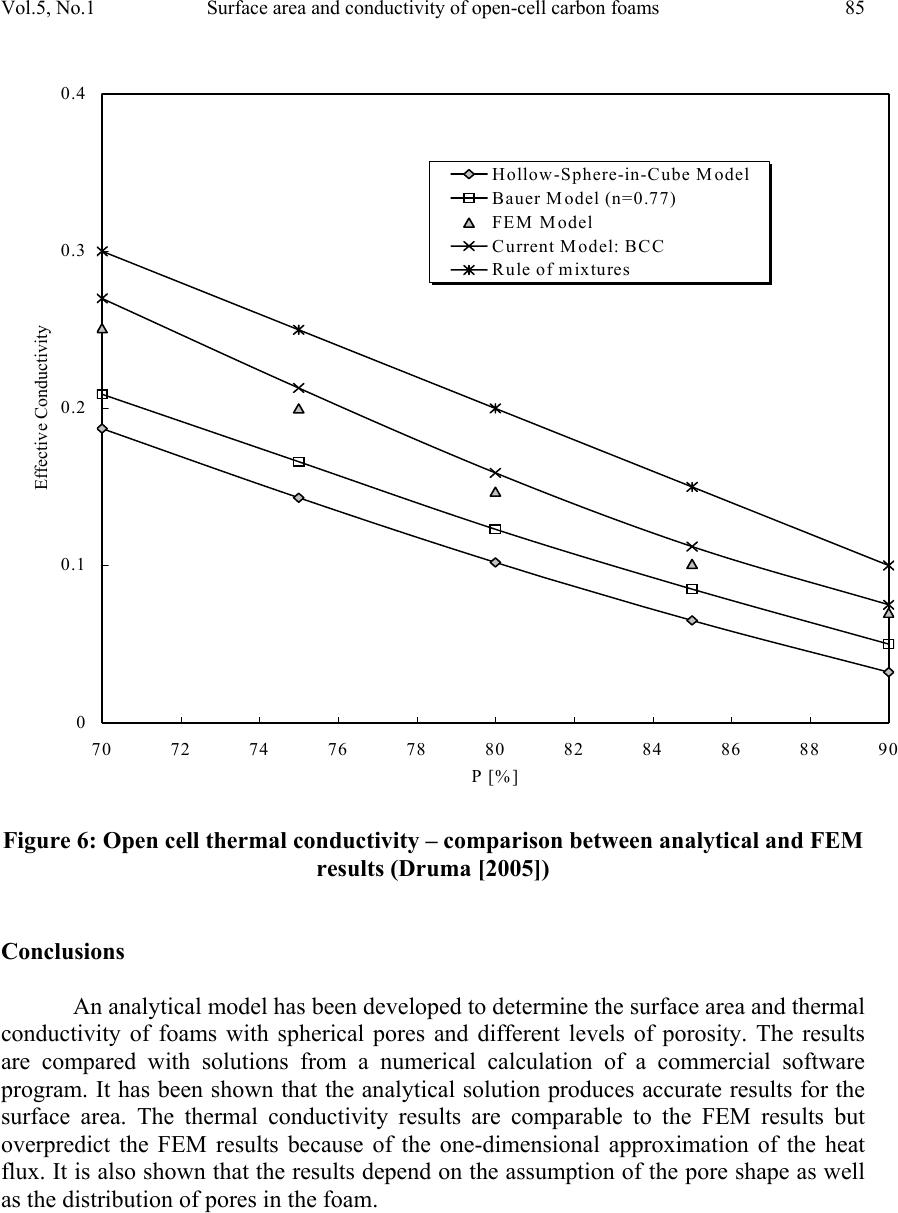

Vol.5, No.1 Surface area and conductivity of open-cell carbon foams 85
0
0.1
0.2
0.3
0.4
7072747678808284868890
P [%]
Effective Conductivity
Hollow-Sphere-in-Cube Model
Bauer Model (n=0.77)
FEM Model
Current Model: BCC
Rule of mixtures
Figure 6: Open cell thermal conductivity – comparison between analytical and FEM
results (Druma [2005])
Conclusions
An analytical model has been developed to determine the surface area and thermal
conductivity of foams with spherical pores and different levels of porosity. The results
are compared with solutions from a numerical calculation of a commercial software
program. It has been shown that the analytical solution produces accurate results for the
surface area. The thermal conductivity results are comparable to the FEM results but
overpredict the FEM results because of the one-dimensional approximation of the heat
flux. It is also shown that the results depend on the assumption of the pore shape as well
as the distribution of pores in the foam.

86 Adriana M. Druma, M. Khairul Alam*, Calin Druma Vol.5, No.1
References
Balantrapu, K., Deepty, R.S., Herald, C.M., Wirtz, R.A., Porosity, Specific Surface Area
and Effective Thermal Conductivity of Anisotropic Open Cell Lattice Structures,
Proceedings of IPACK2005, IPACK2005-73191, California, 2005.
Bauer, T.H., “A general analytical approach toward the thermal conductivity of porous
media”, Int. Journal of Heat and Mass Transfer, vol. 36(17), 4181-4191, 1993.
Bhattacharya, A., Calmidi, V.V., and Mahajan, R.L., Thermophysical properties of high
porosity metal foams, International Journal of Heat and Mass Transfer, 45 (2002)
1017-1031.
Calmidi, V.V., Transport phenomena in high porosity fibrous metal foams, Ph.D.
Dissertation, University of Colorado, Boulder, Colorado, 1998.
Druma, A.D., Alam, M.K., Druma, C., Analysis of thermal conduction in carbon foams,
International Journal of Thermal Sciences, vol. 43(7), pp. 689-695, 2004.
Druma, A.M., Analysis of carbon foams by finite element method, Ph.D. Dissertation,
Ohio University, Athens, Ohio, 2005
Fu, X., Viskanta R., Gore, J.P., Prediction of effective thermal conductivity of cellular
ceramics, Int. Comm. Heat Mass Transfer, Vol. 25, No. 2, pp. 151-160, 1998.
Hsu, C.T., and Cheng P., “Modified Zehner-Schlunder models for stagnant thermal
conductivity of spatially periodic porous media, ASME Journal of Heat Transfer,
37 (17), 2751-2759, 1994.
Hsu, C.T., and Cheng P., “A lumped parameter model for stagnant thermal conductivity
of spatially periodic Porous Media”, ASME Journal of Heat Transfer, 117, 264-
269, 1995.
Kunnii D., and Smith J.M., “Heat Transfer Characteristics of Porous Rocks”, AIChE
Journal, 6, 71-78, 1960.
Sullins, A.D., and Daryabeigi, , K, “Effective Thermal Conductivity of High Porosity
Open Cell Nickel Foam”, AIAA 2001-2819, 35
th
AIAA Thermophysics
conference, Anaheim California, June 2001.
Tee, C.C., Klett, J.W., Stinton, D.P., and Yu N., “Thermal conductivity of porous carbon
foam”, Proceedings of the 24th Biennial Conference on Carbon, July 11-16,
Charleston, SC, 130, 1999.
Zhener P., and Schlunder, E.U., “Thermal Conductivity of Granular Materials at
Moderate Temperatures”, Chemie. Ingr-Tech., 42, 933-941, 1970.