Open Journal of Applied Sciences, 2012, 2, 104-109
doi:10.4236/ojapps.2012.22014 Published Online June 2012 (http://www.SciRP.org/journal/ojapps)
Theoretical Derivation of Thermal Value Equations for
Heating Furnaces
Hainan Wu, Wenqiang Sun*, Jiuju Cai
Institute of Thermal and Environmental Engineering, Northeastern University, Shenyang, China
Received March 22, 2012; revised April 19, 2012; accepted May 2, 2012
ABSTRACT
Based on thermal value theory, the aim of this paper is to deduce the theoretical formulas for evaluating the energy ef-
fective utilization degree in technological pyrological processes exemplified by metallurgical heating furnaces. Heat
transfer models for continuous heating furnaces, batch-type heating furnaces, and regenerative heating furnaces are es-
tablished, respectively. By analyzing the movement path of injected infinitesimal heat attached on steel or gas, thermal
value equations of continuous, batch-type, and regenerative heating furnaces are derived. Then the influences of such
factors as hot charging, gas preheating and intake time of heat on energy effective utilization degree are discussed by
thermal value equations. The results show that thermal value rises with hot charging and air preheating for continuous
heating furnaces, with shorter intake time when heat is attached on steel or longer intake time when heat is attached on
gas for batch-type heating furnaces and that with more heat supply at early heating stage or less at late stage for regen-
erative heating furnaces.
Keywords: Thermal Value; Continuous Heating Furnace; Batch-Type Heating Furnace; Regenerative Heating Furnace;
Energy Utilization Degree; Heat Transfer
1. Introduction
When studying thermal science and engineering, two
types of energy utilization processes with different char-
acteristics should be clearly distinguished. One is energy
conversion processes; the other is technological pyrol-
ogical processes [1]. In energy conversion processes,
main feedstock and product are both energetic materials;
e.g., feedstock is coal and product is electric in thermal
power generation process. But neither material nor prod-
uct is energy in technological pyrological processes, such
as metallurgical production process in which feedstock is
ore and product is metal and energy is just necessary for
pushing the smelting process.
Traditionally, thermal efficiency has been used to
evaluate the energy effective utilization degree of energy
conversion processes [2,3]. However, thermal efficiency
for technological pyrological process is different from
that of energy conversion process [1]; and a conflict be-
tween thermal efficiency and specific energy consump-
tion appears in some cases [4,5]. In this paper, heating
furnaces in metallurgical industry, as technological fa-
cilities, are selected to study the evaluation method for
energy utilization processes. To solve the conflict men-
tioned above, Prof. Ren [6] proposed thermal value the-
ory combining energy conservation principle and heat
transfer theory to evaluate the energy effective utilization
degree in technological pyrological processes. It has been
extended and investigated that thermal value theory is a
theory on energy-saving and production-increasing for
heating furnaces [5,7].
The remainder of the paper is organized as follows:
first, the definition of thermal value is briefly introduced.
Then, a detailed derivation and discussion of thermal
value equations is presented. Finally, conclusions are sum-
marized.
2. Definition of Thermal Value
Take continuous heating furnaces, as shown in Figure 1,
for an example. It can be seen that most heat in the fur-
naces is the chemical heat Hche released from fuel gas’s
combustion. The resulting Hche can be contained in steel
to be available heat Hava. In addition, Hche transfers also
into other points, e.g., Hsur is lost to surroundings by
thermal radiation and convection from the furnaces’ ex-
ternal surface and to soil by conduction, Hspi runs away
from the furnaces with off-gas at furnaces’ door and
other pores, and Hcool is absorbed by cooling water. Much
heat Hexh also leaves with combustion products which
can be used to preheat gas. Then it converts to the physi-
cal heat Hphy of gas and flows into furnace chamber once
*Corresponding author.

H. N. WU ET AL. 105
again. Actually, the heat contained in discharging steel is
not completely meets the expectation (the superheated
part Hsup is also one sort of heat losses, for example).
Additionally, hot charging steel has an effective heat Hcha
itself.
The main purpose of heating furnaces is to heat steel
to a target temperature at which the sensible heat of the
steel is called target heat. Due to the loss items described
above, it is impossible for each injected heat contributes
to target heat completely. And the thermal value (V) of a
certain injected heat is defined as the rate of the part con-
tributing to target heat to the heat injected into the fur-
nace. It is written as
tar
VH H
where H is the enthalpy of injected heat, and Htar is the
part contributing to target heat of H.
3. Heat Transfer Model and Thermal Value
Equations
3.1. Continuous Heating Furnaces
In the continuous heating furnaces (see Figure 1), gas
flows in counter-flow mode with steel. The trends of gas
temperature and steel temperature are given schemati-
cally in Figure 2, in which tg,i and tg,o are temperatures of
gas at its inlet (furnace head) and outlet (furnace end), ts,i
and ts,o are temperatures of steel at its inlet (furnace end)
and outlet (furnace head), and A0 is the total area of heat
exchange.
H
che
H
ava
H
sur
H
phy
H
spi
H
cool
H
exh
H
cha
H
sup
Figure 1. Schematic diagram of continuous heating furnaces.
ig,
t
og,
t
os,
t
is,
t
t
A
0
A
0
Figure 2. Model of gas-steel counter-flow heat transfer in
continuous heating furnaces.
For a gas-steel counter-flow heat transfer model, as
shown in Figure 2, section A is assumed as any one heat
transfer section, and the heat exchange area from gas
inlet to section A is A. Temperatures of gas and steel at
section A are respectively expressed as tg and ts. If inject
a infinitesimal heat which is attached on steel at section
A uniformly and steadily, local steel will have a tem-
perature increase of δts under conditions of no side ef-
fects such as superheat; and correspondingly, steel’s dis-
charging temperature will have a temperature increase of
δts,o; i.e., the (∂ts,o/∂ts) portion of the injected heat makes
the steel’s temperature increase and contributes to target
heat, and other (1 – ∂ts,o/∂ts) portion returns to section A
by way of heat exchange. When gas moving on, the
(∂tg,o/∂tg) portion of heat which has returned to section A
makes the gas’s temperature increase and leaves the fur-
nace with off-gas, and the (1 – ∂tg,o/∂tg) portion also re-
turns to section A through heat exchange and takes part
in the following heat transfer. Then the part contributing
to target heat of injected heat at section A is
g,o s,o s,o
0ss g
11
i
i
i
t tt
tt t





 








  





so thermal value of this injected heat can be written as
g,o s,o s,o
s
ss
11 1
g
t tt
Vtt
t
.



 













(1)

According to [5], then


g0
sg
g,o
ggg
0
ssg
1exp 1
1,
1exp1
WkA A
WW
t
tWW
kA A
WWW


















 









(2)
and
g
sg
g
s,o
ss
gg
ss
1exp 1
1,
1exp1
WkA
WW
W t
tW
WW
kA
WW








 








g
W

(3)
where k is over-all heat transfer coefficient of gas-steel
and assumed as a constant, and Wg, Ws are water equiva-
lent of gas and steel, respectively. Define

0,0 1,AA



 (4)
and substitute Equations (2)-(4) into Equation (1), then
thermal value equation for injected heat attached on steel
is expressed as

gg
0
ssg
s
gg
0
ssg
1exp1 1
.
1exp1
WW
kA
WWW
VWW
kA
WWW




 
















(5)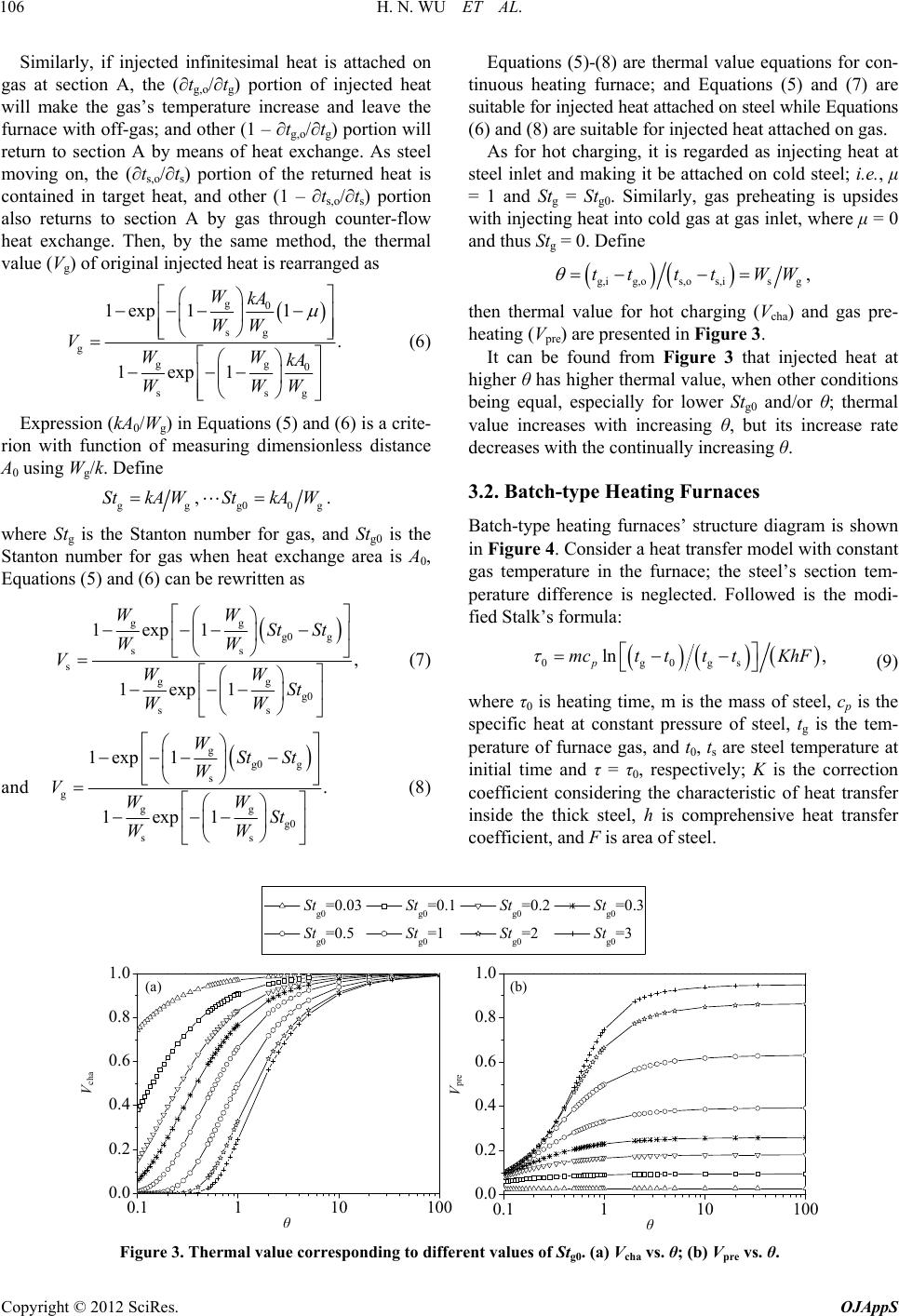

H. N. WU ET AL.
106
Equations (5)-(8) are thermal value equations for con-
tinuous heating furnace; and Equations (5) and (7) are
suitable for injected heat attached on steel while Equations
(6) and (8) are suitable for injected heat attached on gas.
Similarly, if injected infinitesimal heat is attached on
gas at section A, the (∂tg,o/∂tg) portion of injected heat
will make the gas’s temperature increase and leave the
furnace with off-gas; and other (1 – ∂tg,o/∂tg) portion will
return to section A by means of heat exchange. As steel
moving on, the (∂ts,o/∂ts) portion of the returned heat is
contained in target heat, and other (1 – ∂ts,o/∂ts) portion
also returns to section A by gas through counter-flow
heat exchange. Then, by the same method, the thermal
value (Vg) of original injected heat is rearranged as
As for hot charging, it is regarded as injecting heat at
steel inlet and making it be attached on cold steel; i.e., μ
= 1 and Stg = Stg0. Similarly, gas preheating is upsides
with injecting heat into cold gas at gas inlet, where μ = 0
and thus Stg = 0. Define




g,ig,os,os,isg ,ttttWW
 

g0
sg
g
gg
0
ss
1exp 11
.
1exp1
WkA
WW
VWW
kA
WWW



 













g



(6)
then thermal value for hot charging (Vcha) and gas pre-
heating (Vpre) are presented in Figure 3.
It can be found from Figure 3 that injected heat at
higher θ has higher thermal value, when other conditions
being equal, especially for lower Stg0 and/or θ; thermal
value increases with increasing θ, but its increase rate
decreases with the continually increasing θ.
Expression (kA0/Wg) in Equations (5) and (6) is a crite-
rion with function of measuring dimensionless distance
A0 using Wg/k. Define 3.2. Batch-type Heating Furnaces
ggg00
,.StkAWStkAWg
where Stg is the Stanton number for gas, and Stg0 is the
Stanton number for gas when heat exchange area is A0,
Equations (5) and (6) can be rewritten as

gg
g0 g
ss
s
gg
g0
ss
1exp1
,
1exp1
WW
St St
WW
VWW
St
WW


 







 



(7)
Batch-type heating furnaces’ structure diagram is shown
in Figure 4. Consider a heat transfer model with constant
gas temperature in the furnace; the steel’s section tem-
perature difference is neglected. Followed is the modi-
fied Stalk’s formula:


0g0gs
ln ,
p
mctt ttKhF 



(9)
and

g
g0 g
s
g
gg
g0
ss
1exp 1
.
1exp1
WSt St
W
VWW
St
WW


 
 





 





(8)
where τ0 is heating time, m is the mass of steel, cp is the
specific heat at constant pressure of steel, tg is the tem-
perature of furnace gas, and t0, ts are steel temperature at
initial time and τ = τ0, respectively; K is the correction
coefficient considering the characteristic of heat transfer
inside the thick steel, h is comprehensive heat transfer
coefficient, and F is area of steel.
0.1110 100
0.0
0.2
0.4
0.6
0.8
1.0
V
cha
θ
(a)
0.1110 100
0.0
0.2
0.4
0.6
0.8
1.0
V
pre
θ
(b)
Stg0=0.03 Stg0=0.1 Stg0=0.2 Stg0=0.3
Stg0=0.5 Stg0=1 Stg0=2 Stg0=3
Figure 3. Thermal value corresponding to different values of Stg0. (a) Vcha vs. θ; (b) Vpre vs. θ.

H. N. WU ET AL. 107
According to Equation (9), heating curve of steel in
batch-type furnaces is schematically shown in Figure 5.
After injecting heat into batch-type furnace, Equation (9)
can be rewritten as


g s,i g s,o
ln ,
p
mctt ttKhF 



(10)
where τ is the heating time with heat being injected, and
ts,i, ts,o are the initial temperature and end temperature of
steel with heat being injected, respectively.
Inject infinitesimal heat into the model shown in Fig-
ure 5 uniformly and steadily and make it be attached on
steel so that local steel has a temperature increase of δts,i
from ts,i and hence the end temperature of steel increases
by δts,o during time-span (τ) since injecting heat. Consid-
ering other conditions unchanged, during the time τ of
heating process, the (∂ts,o/∂ts,i) portion of injected heat is
for one part of target heat. According to the definition of
thermal value, the thermal value (Vs) of the injected in-
finitesimal heat is written as
ss,os,i
.Vtt (11)
From Equations (10) and (11), it can be arrived at

sexp . p
VKhFmc 


 
(12)
By the same method, if the uniformly injected heat is
attached on gas which has a temperature increase of δtg
Figure 4. Schematic diagram of batch-type heating furnaces.
τ
t t
g
t
s
Figure 5. Model of heating process in batch-type heating
furnaces.
during the heating period τ, and correspondingly, the end
temperature of steel has increased by δts,o from ts,o. Dur-
ing heating process of time-span τ, the [(Ws∂ts,o)/(Wg∂tg)]
portion of the heat injected into gas contributes to target
heat; therefore, the thermal value (Vg) of the injected
infinitesimal heat is as follows:

gg
1exp .
p
VKhFmcW 


 


s
W (13)
Expression (KhFτ/(mcp)) in Equations (12) and (13) is
a criterion with function of measuring dimensionless
time τ using (mcp/(KhF)). Define

s, p
St KhF mc  
where Sts is the Stanton number for steel, Equations (12)
and (13) can be rewritten as

s
exp ,VS
s
t (14)
and

 
gs
1exp .VStW  

gs
W (15)
Equations (12)-(15) are thermal value equations for
batch-type heating furnace; and Equations (12) and (14)
are suitable for injected heat attached on steel while
Equations (13) and (15) are suitable for injected heat at-
tached on gas.
Taking the heating of thin steel as an example, the re-
lationship between thermal value and intake time is pre-
sented in Figure 6 [7]. It can be seen that injected heat
attached on steel at shorter time τ (closer to the end of
heating) has higher thermal value Vs; and heat attached
on gas at longer time τ has higher thermal value Vg.
3.3. Regenerative Heating Furnaces
Regenerative heating furnaces have been applied and
spread at home and abroad since the new century. Fur-
naces of this type operate on the principle of high tem-
perature air combustion (HTAC) technology and have
uniform temperature in furnace hearth. The structure
diagram and its simplified model are shown in Figures 7
and 8, respectively.
0.0
0.2
0.4
0.6
0.8
1.0
01234567
τ
V
V
s
V
g
Figure 6. V vs. τ.

H. N. WU ET AL.
108

Figure 7. Schematic diagram of regenerative heating furaces. n
(i)
(ii)
(iii )
(iv)
(v)
Figure 8. Energy utilization model in regenerative heating
Inject a infinitesimal heat steadily and uniformly into
th
nerative
furnaces.
e model shown in Figure 8 and make it be attached on
gas at a certain section, the [(Ws∂ts,o)/(Wg∂tg)] portion of
the injected heat (i) makes the steel’s temperature in-
crease and be contained in target heat, but other
[1 – (Ws∂ts,o)/(Wg∂tg)] portion (ii) flows into rege
chamber to preheat cold gas. Assume the recovery effi-
ciency of waste heat of regenerative chamber is η, then
the {(1 – η)[1 – (Ws∂ts,o)/(Wg∂tg)]} portion of the heat
entering regenerative chamber is off the furnace with
waste gas while the {η[1 – (Ws∂ts,o)/(Wg∂tg)]} portion (iii)
returns with preheated gas and continuous to take part in
the heat transfer process, viz., processes (iv) and (v).
Then the part contributing to target heat of the original
injected heat is
ss,oss,o
0gg gg
1,
i
i
i
WtWt
Wt Wt










 



so the thermal value (Vg) of injected heat is
ss,oss,o
g
gg gg
11
Wt Wt
VWt Wt 




 





.



(6)
Similarly, if the uniformly injected heat is attached on
steel, which results in a temperature increase of δts,i for
local steel and δts,o for discharging steel, the (∂ts,o/∂ts,i)
portion of the injected heat will be part of target heat and
other (1 – ∂ts,o/∂ts,i) portion will enter regenerative cham-
ber with gas. For the heat passing through regenerative
chamber, its [(1 – η)(1 – ∂ts,o/∂ts,i)] portion losses while
other [η(1 – ∂ts,o/∂ts,i)] portion returns to furnace hearth
with preheated gas. So, the thermal value (Vs) of the in-
jected heat is written as
s,o s,os s,os s,o
s
s,ig gg g
s,i
111
ttWt Wt
VtWt Wt
t



.



 
 
 

 

(7)
Although regenerative heating furnaces belong to con-
tin


uous furnaces in steel transport style, the energy using
situation is alike to batch-type furnaces since the tem-
perature of combustion products is uniform in the whole
furnace hearth [8], because which it has no difference
whether steel taps off from feed door or from discharge
door and regenerative furnaces have shared characteris-
tics of both continuous ones and batch-type ones. Com-
bining with Equations (10), Equations (16) and (17) can
be rewritten as




s
g
g
s
s
1exp ,
11exp
St
VWSt
W






 


(18)
and
  
 
g
ss
s
s
g
s
s
1exp1 exp
.
11exp
WSt St
W
VWSt
W


 



 

(19)
Equations (18) and (19) are thermal value equations
for regenerative heating furnaces; and Equation (18) is
suitable for injected heat attached on gas while Equation
(19) is suitable for injected heat attached on steel.
From Equation (18) and (19), it can be got
 
gg g
ss
s
ss
1exp 0,St
St W

 
VV W
St St



 

and


2
2 g
sss s
s
ss
1exp 0.
W
VV StStSt
St W

 
 

 

 
which show that if injected heat is attached on gas, the
though the
eq
higher τ, the higher Vg, and that if injected heat is at-
tached on steel, the lower τ, the higher Vs; thereby, di-
recting at higher thermal value, the supply of heat should
be more at early stage and less at late stage.
The thermal value may be different even
uivalent injected heat, depending on the intake time.
Transition time (τ*) is calculated by



*ln 1mcWW
 
gs .
pKhF
Given the property of continuous operating the time τ ,
here also represents the location of steel. Correspond-
ingly, the transition location (along steel’s moving direc-
tion) l* is
*
gg
*
s
ss
ln 1ln 1,
p
mc WW
ll St
KhF WW


 
 
 
 

H. N. WU ET AL.
109
Vg
Vs
τ
l
V
τ
*
l
*
Figure 9. V vs. τ and l.
where l is the effective length of furnace.
Distinguished fg furnaces,
al value of heat attached on steel is higher than that on
furnaces, and
th
he n metallurgical
value equations of continuous, bat
heating furnaces are derived for
ents
he Fundamental Research
ersities (No.N090602007),
[1] Z. W. Lu, “Flaical Industry Press,
Beijing, 1995.
ption and Performance of Reheating Fur-
rom continuous heatin ther-
m
gas when l ＞ l* for regenerative heating
ermal value of heat attached on steel is lower than that
on gas when l ＜ l* (shown in Figure 9).
4. Conclusion
By modeling theat transfer processes i
furnaces, thermal
type, and regenerative
ch-
evaluating their energy utilization degree. Based on the
detailed derivation and discussion of thermal value equa-
tions, it can be concluded that thermal value increases
with increasing temperature of preheated gas or with hot
charging for continuous heating furnaces. Injecting heat
into batch-type heating furnaces to be attached on steel,
thermal value is higher when intake time is closer to the
end of heating; while to be attached on gas, thermal value
is higher when closer to the time for supplying gas. For
regenerative heating furnaces, to obtain higher thermal
value, the supply of heat should be more at early stage
and less at late stage.
5. Acknowledgem
This work is supported by t
Funds for the Central Univ
China. The corresponding author also owes great thanks
to Prof. Shizheng Ren for his excellent advices.
REFERENCES
me Furnace,” Metallurg
[2] W. H. Chen, Y. C. Chung and J. L. Liu, “Analysis on
Energy Consum
naces in a Hot Strip Mill,” International Communications
in Heat and Mass Transfer, Vol. 32, No. 5, 2005, pp.
695-706. doi:10.1016/j.icheatmasstransfer.2004.10.019
[3] C. L. Hou, G. B. Wang and J. Zhang, “Characteristics of
Walking-Beam Reheating Furnace Applied in Continuous
Continuous Heating Furnaces
y-Saving for Continuous
ation Degree of Energy in Batch-Type
Casting and Rolling Line of Guofeng,” Steel Rolling, Vol.
25, No. 4, 2008, pp. 26-27.
[4] W. Q. Sun, J. J. Cai and G. W. Xie, “Application Re-
search on Energy-Saving of
Based on Thermal Value Theory,” Proceedings of 1st In-
ternational Conference on Applied Energy, Hong Kong,
5-7 January, 2009, pp. 614-620.
[5] J. J. Cai, W. Q. Sun and G. W. Xie, “Thermal Value The-
ory and Its Application to Energ
Heating Furnace,” Journal of Northeastern University
(Natural Science), Vol. 30, No. 10, 2009, pp. 1454-1457.
[6] S. Z. Ren, “Heat Transfer,” Metallurgical Industry Press,
Beijing, 2007.
[7] W. Q. Sun, J. J. Cai, T. Du and C. Wang, “Research on
Effective Utiliz
Furnace Based on Thermal Value Theory”, Proceedings
of 2009 International Conference on Energy and Envi-
ronment Technology, Guilin, 16-19 October, 2009, Vol. 1,
pp. 794-797. doi:10.1109/ICEET.2009.198
[8] W. Trinks and M. H. Mashinney, “Industrial Furnaces,”
5th Edition, John Wiley & Sons Inc., New York, 1961.