Paper Menu >>
Journal Menu >>
 Journal of Minerals & Materials Characterization & Engineering, Vol. 3, No.2, pp 99-103, 2004 jmmce.org Printed in the USA. All rights reserved 99 Investigation Of Hardness Anisotropy In Tourmaline *M.O. Adeoye and ‡O.O. Adewoye *Department of Metallurgical and Materials Engineering, O .bafe .mi Awolo .wo . University, Ile-Ife .. Nigeria ‡Engineering Materials Development Institute, Akure, Nigeria. Abstract: Tourmaline is a ring silicate material with a hexagonal crystal structure. Tourmaline crystal is made use of as an electronic component, e.g, as a transducer, mainly because of the anisotropy it exhibits in its properties. Microindentation technique was employed in the research reported in this paper, using a Knoop indenter, to investigate the anisotropy in the hardness of the tourmaline crystal on its two major crystallographic planes: (0001) and {1010}. The material was found to exhibit hardness anisotropy in conformity with its rotary symmetry elements. The material was identified and analysed using various x-ray techniques, and was found to contain some impurities as expected of natural crystals. Tourmaline was found to have a Si/Al ratio of 1.4. The orientations of the crystal samples were determined by obtaining and indexing the Laue x-ray back-reflection patterns of the crystal samples. Keywords: Tourmaline, Hardness anisotropy, Microhardness, Knoop. 1.0 Introduction 1.1 Hardness Hardness in solid materials is a deformation parameter; it is the resistance of a material to indentation. Hardness on the micro- scale is known as microhardness and is obtained by the application of very small indenters under low loads on the surface of a material e.g. Vickers pyramid tests and Knoop tests. Similar to other crystalline materials, the variation of microhardness for tourmaline is dependent on orientation in single crystals. Such crystals are said to exhibit anisotropy in hardness, i.e., hardness varying from one direction to the other on the same test plane [1,2]. In this work the aim was not to determine the absolute hardness value of tourmaline but rather to study its variation with crystallographic direction on the most prominent crystallographic planes of the single crystal. The Knoop rhombohedral pyramid indenter is used for this study because there is less ambiguity in aligning it with respect to any given crystallographic directions due to its long diagonal being seven times longer than the short diagonal. That is the indenter has a parallelogram base with the short diagonal related to the long diagonal by a factor of 7.1114. The Knoop hardness HKd under a load L is then given by 100 M.O. Adeoye and O.O. Adewoye Vol. 3, No.2 where d is the length of the long diagonal of the indent. 1.2 Materials Tourmaline is a group name applied to the natural silicate minerals of the general formula XY3Z6(BO3)3Si6O18(OH)4 where X can be Na or Ca; Y can be substitutions of monovalent, divalent, trivalent or quadrivalent cations (Li, Mg, Mn, Fe, Al etc.); and Z can be occupied by Al, Mg, Cr, Fe3+, Fe2+, etc. [3,4]. F- or O2- can substitute for OH-. The commonest end-members of tourmaline are: buergerite, dravite, elbaite, liddicoatite, schorl and uvite. Tourmaline crystal shows parallel grouping (or growth), and has a rhombohedral (trigonal) crystal structure with a space group of R3m. [5]. Although this crystal class (3m) is based on the rhombohedral lattice [6], it can also be based on the hexagonal lattice [7]. In general, crystals in the rhombohedral system can be referred to as possessing a hexagonal lattice. Detail information on rhombohedral-hexagonal transformation has been given in the literature (e.g., [8,9,10]). It is categorized as a crystal symmetry class known as ditrigonal pyramidal [6,7]. It cleaves very poorly on planes {1120} and {1011}. Tourmaline varies in colour from transparent to opaque as in black schorl. Due to its polarity, a charge of electricity may be induced in a tourmaline crystal when pressure is applied parallel to the c-axis. In other words, not only does the ele ctrical conductivity of tourmaline crystal change with crystallographic directions, but also with the pressure applied to the crystal, thus, tourmaline is a piezoelectric material, and exhibits a linear piezoelectric effect. This property together with high strength, chemical stability, and high frequenc y, account for its use in many instruments such as transducers for measuring hydrostatic pressure and in depth-recording devices, and also in instruments for detecting submarines and underwater obstructions [ 11,12]. Tourmaline is also used for calibration of piezoelectric manometers and for testing the possible applicability of a device or procedure for use on materials having complex structures and compositions. Because of its light-polarizing effect, tourmaline is also used in the polariscope utilized especially by jewelers. The mineral tourmaline is one of the best known naturally occurring dichroic materials. The refractive index of tourmaline for the ordinary beam is no = 1.64, and for the extraordinary beam is ne = 1.62 [13]. From the foregoing, the anisotropic nature of tourmaline crystal is apparent. The anisotropy in its hardness on the crystallographic planes {0001} i.e., the basal plan e, and the prismatic planes {1010} are therefore investigated in this work. The species of tourmaline used here was buergerite - NaFe3Al6(BO3)3Si6O18(O,F)4. The crystals were euhedral. They were of prismatic habit which is the usual habit of these minerals. The crystals were prismatic in shape. The prism faces had natural striations parallel to their length, which are evidences of a particular form: hexagonal prism in these cases. f (HKd ) = 14230L / d2 (1) 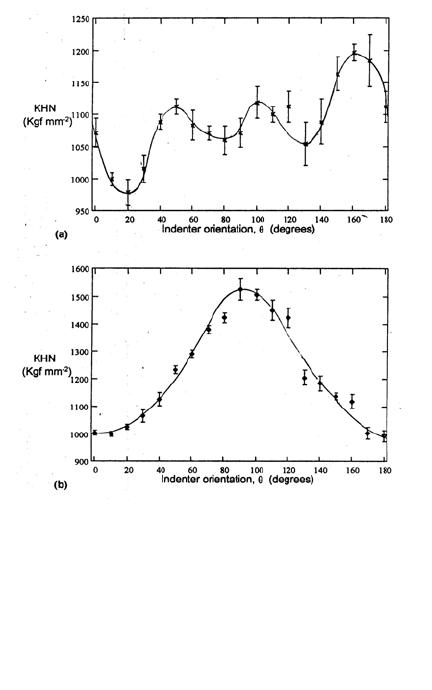 Vol. 3, No.2 Investigation of Hardness Anisotropy in Tourmaline101 2.0 Experimentals X-ray powder diffra ction technique was used to identify the crystals on a Philips X-ray Diffractometer PW 1390 with PW 1050 goniometer incorporating a graphite monochromator. The radiation was CuK∀1 (8 = 1.54060Å). Natural minerals usually contain wide ranges of impurities in varying proportions. The materials used in this work were not exceptions, being natural minerals. Hence, the elemental chemical analysis of the minerals specimens was carried out using x-ray photoelectron spectroscopy (XPS) which is sensitive to only the first 10nm of the surface on a Physical Electronics 5400 system with a MgK∀ (8 = 9.8900Å) radiation at 15kV and 325W, and energy dispersive x-ray analysis (EDXA) in a JOEL 850 scanning electron microscope (SEM) which can probe deeper into the material. Crystal orientations were determined by carrying out Laue x-ray back-reflection on the crystals using a Philips PW 1729 back-reflection camera. Specimens of the tourmaline crystals were cut parallel to the prismatic (1010) plane and others parallel to the basal (0001) planes and then polished down to ¼ :m finish. The anisotropy investigation was carried out using a Knoop indenter on a Shimadzu Microhardness Tester, T ype M. (See [14] for details). A load o f 100g wa s used throughout. Tests were performed at room temperature with a dwell time of 15 seconds. The angle of orientation of the long diagonal of the Knoop indenter was varied on each of the specimen surfaces (0001) and {1010} between 0° and 180°. For each indentation the long diagonal was measured. Six indentations were made for each orientation. Thus each long diagonal value was an average of six values. The Knoop hardness number (KHN) was then obtained for each orient ation using equation (1) and plotted as shown in Figure 1. 2.0 Discussion Figure 1: Hardness, KHN, anisotropy in tourmaline as exhibited on (a) the basal plane (0001), 0° corresponds to [1010] while 90° corresponds to [1210], and (b) the prismatic planes {1010}, 0° corresponds to [1210] while 90° corresponds to [0001] 102 M.O. Adeoye and O.O. Adewoye Vol. 3, No.2 The x-ray analyses identified the crystals to be the ring-silicate mineral tourmaline speci es buer gerite - NaFe3Al 6(BO3)3Si6O18(O,F)4. They were found to contain a low level of some impurities such as calcium and phosphorus or their compounds. The Si/Al ratio was found to be 1.4. [14] Figure 1 shows the hardness anisotropy obtained from measurements of planes (0001) and {1010} of tourmaline. In Figure 1a, 0°corresponds to [1010] while 90°corresponds to [1210]. The curve displa ys several peaks (hard dire ctions) each about 50° from the next, and several troughs (soft directions) also about 50° from one another. The symmetry displayed is found to be consistent with the operation of (0001) ′1210ƒ slip system, in other words, flow on the basal plane of tourmaline is controlled by (0001)′1210ƒ system. The picture for the prismatic plane (1010), Figure 1b, is a “bell shape” symmetry over a range of 0° to 180° starting with [1210] direction as 0°. Only one peak is exhibited here at 90° which is the direction [0001]. Thus [0001] represents the highest hardness direction on this plane with a Knoop hardness (K HN) of about 1540 kg mm-2, and [1210] is the softest direction with about 1000 kg mm-2 KHN. This also presents a flow consistent with (0001)′1210ƒ system. The di fference between the soft est and the hardest directions is about 500 kgf mm-2 (Knoop hardness). 4.0 Conclusion The material, tourmaline crystals, were found to exhibit anisotropy in Knoop hardness in conformity with their rotary symmetry elements of 3 on the basal planes. On this plane the probable operating slip system controlling the indentation process was found to be (0001)′1120ƒ. On the prismatic planes {1010} the slip system thought to be in operation during indentation was also (0001)′1120ƒ. Acknowledgement The authors wish to thank Professor T.F. Page, the he ad of the Materials Division and the Ceramics Tribology Research Group at the University of Newcastle Upon Tyne, England, for allowing the use his laboratory. And Dr. J. J. Weimer of Chemistry Department/Chemical & Materials Engineering Department, University of Alabama in Huntsville, Huntsville, Alabama, U.S.A. for his assistance on the work on XPS and EDXA. References 1. Adewoye O. O. Anisotropy flow and fracture in beryl [Be3Al2(SiO3)6]. J. Mater. Sci. 21, 1161. 1986 2. Adewoye O. O. and Page T. F. The anisotropy behaviour of etched hardness indentation in SiC. J. Mater. Sci. 11, 981.1976 Vol. 3, No.2 Investigation of Hardness Anisotropy in Tourmaline103 3. Henry D. J. and Guidotti C. V. Tourmaline as a petrogenetic indicator mineral: An example from the straurolite-grade metapelite of NW Maine. Am. Mineralogist 70, 1.1985 4. Deer W. A., Howie R. A. and Zussman J. “Rock-Forming Minerals.” Vol. 1B: Disilicates and Ring Silicates. 2nd edition. London, Longman Group Ltd. 1986 5. Deer W. A., Howie R. A. and Zussman J. “An Introduction to the Rock-Forming Minerals.” England, Longman Scientific and Technical. 1992 6. Phillips F. C. “An Introduction to Crystallography.” Fourth edition. English Language Book Society and Longman Group Limited. 1971 7. Klein C. and Hurlburt jr. C. S. “Manual of Mineralogy.” New York, John Wiley and Sons, Inc. 1993 8. Cullity B. D. “Elements of X-Ray Diffraction.” 2nd edition. Addison-Wesley Publishing Company, Inc.. 1978 9. Kelly A. and Groves G. W . “Crystallograph y and Crystal Def ects.” London, Longman Group Limited. 1970 10. International Union of Crystallography “International Tables for X-ray Crystallography” Vol. I: Symmetry Groups. Henry N. F. M. and Lonsdale K. (eds.) Birmingham, England, Kynoch Press. pp.15 - 21. 1969 11. Katz R. N. “Proceedings of the Third International Conference on Mechanical Behaviour of Materials.” Volume I. Miller K. J. and Smith R. F. (eds.) 20th August, 1979. Pergamon Press. 1980 12. Sargent P. M. Ph. D. Thesis: Factors Affecting The Microhardness of Solids. University of Cambridge, England. 1979 13. Longhurst R. S. “Geometrical and Physical Optics.” London, Longman Groups Limited. 1973 14. Adeoye M. O. Ph.D. Thesis: Flow And Fracture in Tourmaline and Beryl Using Indentation Techniques. Obafemi Awolowo University, Ile-Ife, Nigeria. 1998 |

