Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24522 , 4 pages DOI:10.4236/am.2012.311237
The H-Decomposition Problem for Graphs
Departamento de Matemática and Centro de Matemática e Aplicações, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, Quinta da Torre, Caparica, Portugal
Email: tmjs@fct.unl.pt
Received September 10, 2012; revised October 10, 2012; accepted October 17, 2012
Keywords: Graph Decompositions; Weighted Graph Decompositions; Monochromatic Graph Decompositions; Turán Graph; Ramsey Numbers
ABSTRACT
The concept of H-decompositions of graphs was first introduced by Erdös, Goodman and Pósa in 1966, who were motivated by the problem of representing graphs by set intersections. Given graphs G and H, an H-decomposition of G is a partition of the edge set of G such that each part is either a single edge or forms a graph isomorphic to H. Let 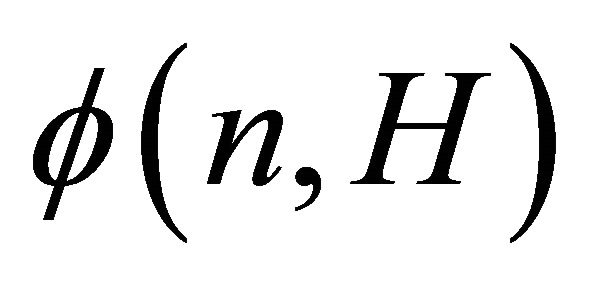 be the smallest number
be the smallest number , such that, any graph of order n admits an H-decomposition with at most
, such that, any graph of order n admits an H-decomposition with at most  parts. The exact computation of
parts. The exact computation of  for an arbitrary H is still an open problem. Recently, a few papers have been published about this problem. In this survey we will bring together all the results about H-decompositions. We will also introduce two new related problems, namely Weighted H-Decompositions of graphs and Monochromatic H-Decompositions of graphs.
for an arbitrary H is still an open problem. Recently, a few papers have been published about this problem. In this survey we will bring together all the results about H-decompositions. We will also introduce two new related problems, namely Weighted H-Decompositions of graphs and Monochromatic H-Decompositions of graphs.
1. Introduction
1.1. Terminology and Notations
For notation and terminology not discussed here the reader is referred to [1]. A graph is a (finite) set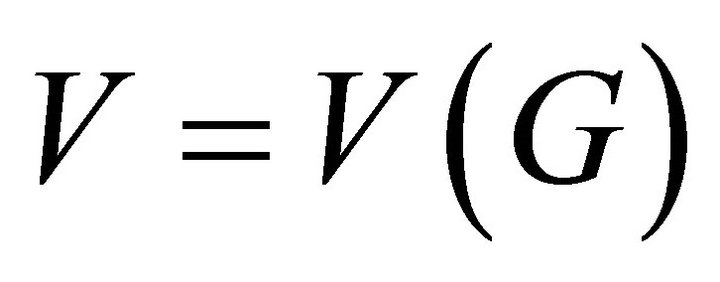 , called the vertices of G together with a set
, called the vertices of G together with a set 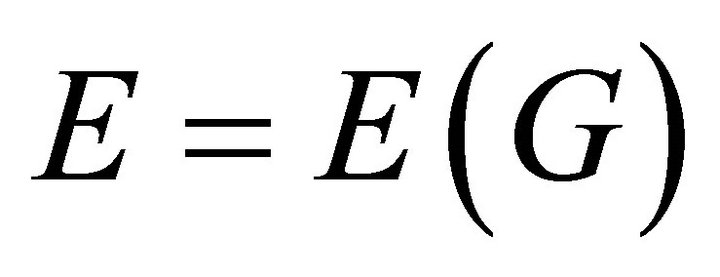 of (unordered) pairs of vertices of G, called the edges. We do not allow loops and multiple edges. The number of vertices of a graph is its order and is denoted by
of (unordered) pairs of vertices of G, called the edges. We do not allow loops and multiple edges. The number of vertices of a graph is its order and is denoted by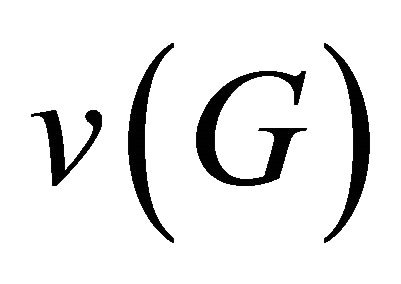 . The number of edges in a graph is its size and is denoted by
. The number of edges in a graph is its size and is denoted by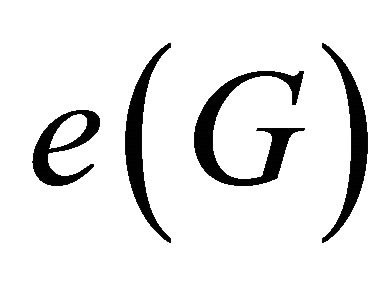 . A vertex
. A vertex 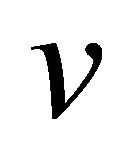 is incident with an edge e if
is incident with an edge e if  and the two vertices incident with an edge are called its endpoints. Two vertices
and the two vertices incident with an edge are called its endpoints. Two vertices 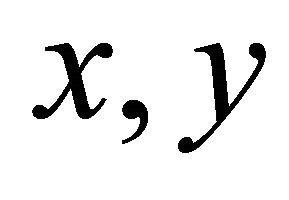 of G are said to be adjacent or neighbors if
of G are said to be adjacent or neighbors if  is an edge of G. The degree of a vertex v is the number of edges incident with v and will be denoted by
is an edge of G. The degree of a vertex v is the number of edges incident with v and will be denoted by 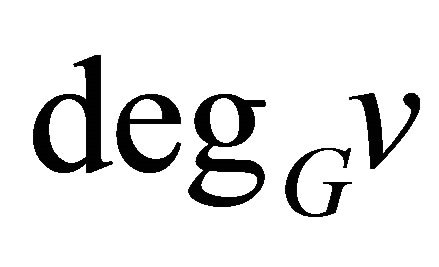 or simply by
or simply by 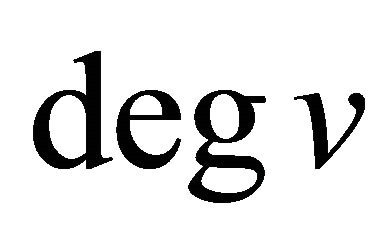 if it is clear which graph is being considered. The complete graph (clique) of order n will be denoted by
if it is clear which graph is being considered. The complete graph (clique) of order n will be denoted by , the complete bipartite graph with parts of size m and n will be denoted by
, the complete bipartite graph with parts of size m and n will be denoted by 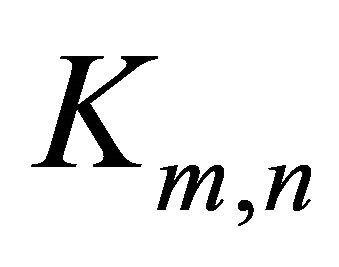 and the cycle of length
and the cycle of length 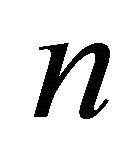 will be denoted by
will be denoted by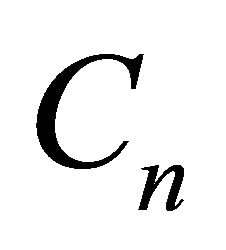 .
.
The Turán graph of order n, denoted by , is the unique complete
, is the unique complete 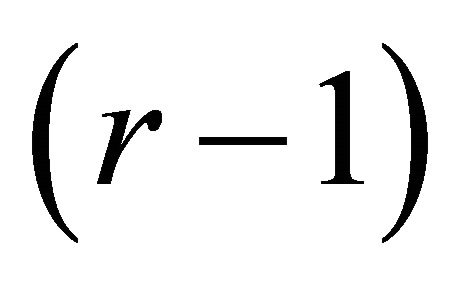 -partite graph on n vertices where every partite class has either
-partite graph on n vertices where every partite class has either 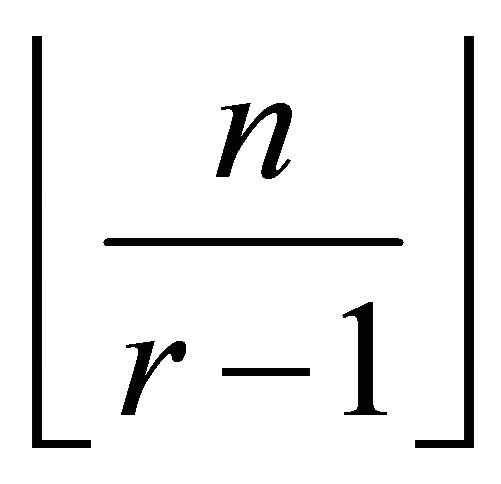 or
or 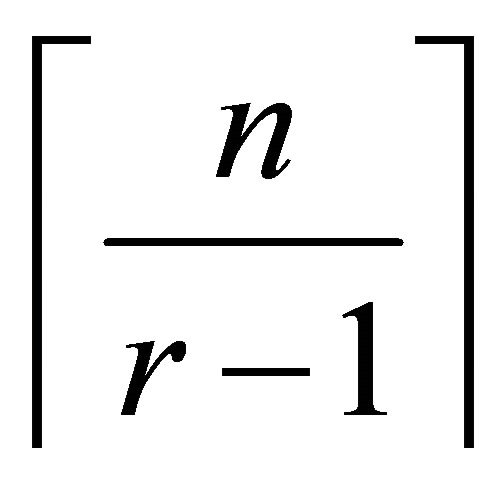 vertices. The well-known Turán’s Theorem [2] states that
vertices. The well-known Turán’s Theorem [2] states that 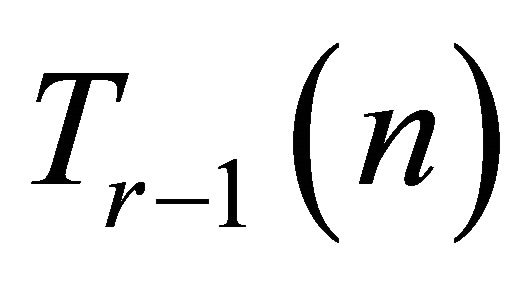 is the unique graph on n vertices that has the maximum number of edges and contains no complete subgraph of order r. We let
is the unique graph on n vertices that has the maximum number of edges and contains no complete subgraph of order r. We let 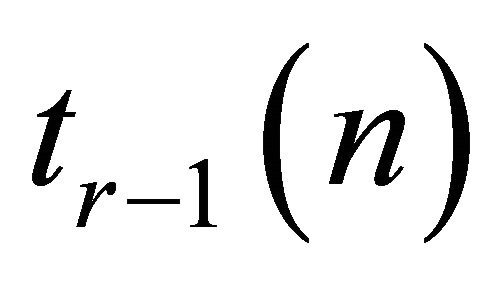 denote the number of edges in
denote the number of edges in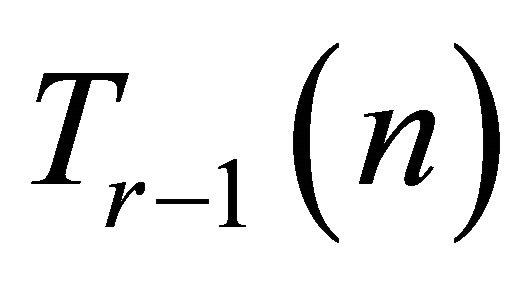 .
.
Finally, a proper colouring or simply a colouring of the vertices of G is an assignment of colours to the vertices in such a way that adjacent vertices have distinct colours; 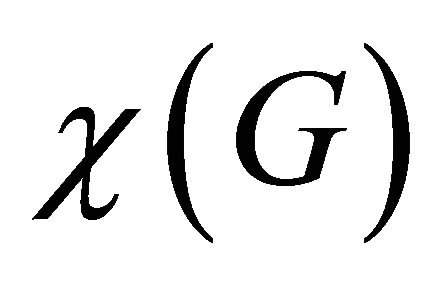 is then the minimum number of colours in a (vertex) colouring of G. For example,
is then the minimum number of colours in a (vertex) colouring of G. For example,  ,
, 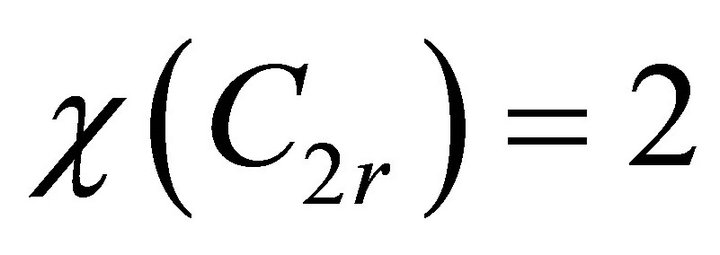 and
and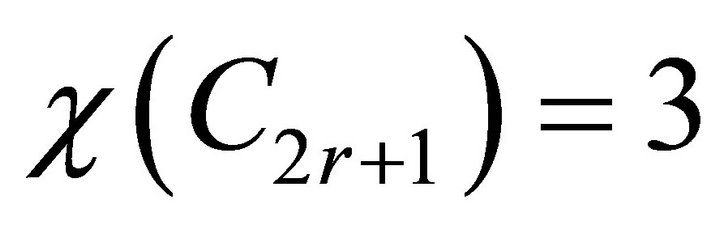 .
.
1.2. Motivation and Definitions
Given two graphs G and H, an H-decomposition of G is a partition of the edge set of G such that each part is either a single edge or forms an H-subgraph, i.e., a graph isomorphic to H. We allow partitions only, that is, every edge of G appears in precisely one part. Let 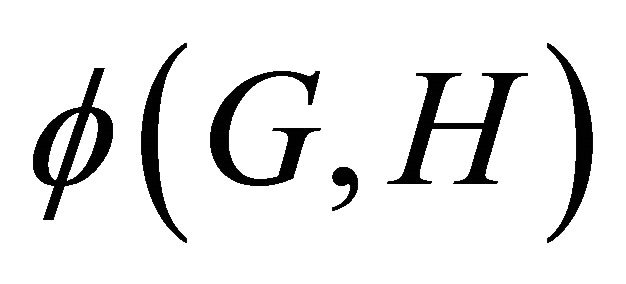 be the smallest possible number of parts in an H-decomposition of G. It is easy to see that
be the smallest possible number of parts in an H-decomposition of G. It is easy to see that 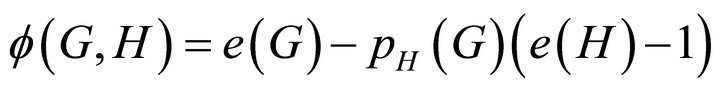 , where
, where 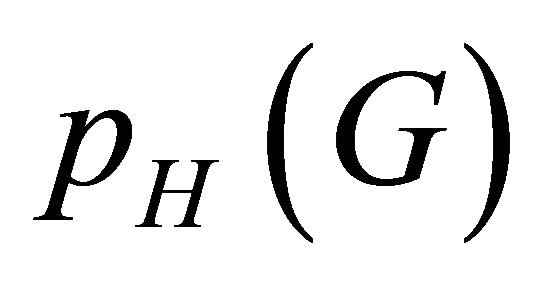 is the maximum number of pairwise edge-disjoint H-subgraphs that can be packed into G. Building upon a body of previous research, Dor and Tarsi [3] showed that if H has a component with at least 3 edges, then the problem of checking whether an input graph G is perfectly decomposable into H-subgraphs is NP-complete. Hence, it is NP-hard to compute the function
is the maximum number of pairwise edge-disjoint H-subgraphs that can be packed into G. Building upon a body of previous research, Dor and Tarsi [3] showed that if H has a component with at least 3 edges, then the problem of checking whether an input graph G is perfectly decomposable into H-subgraphs is NP-complete. Hence, it is NP-hard to compute the function  for such H. Therefore, the aim is to study the function
for such H. Therefore, the aim is to study the function

which is the smallest number such that any graph G of order n admits an H-decomposition with at most 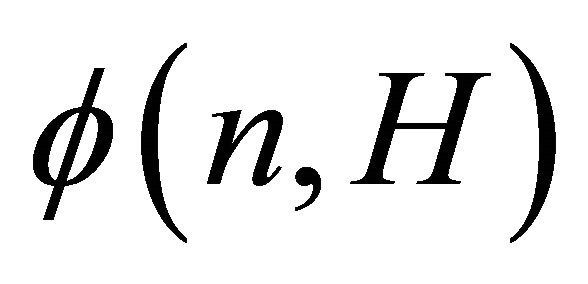 parts.
parts.
This function was first studied, in 1966, by Erdös, Goodman and Pósa [4], who were motivated by the problem of representing graphs by set intersections. They proved that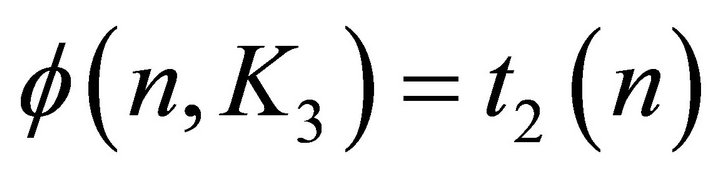 . A decade later, this result was extended by Bollobás [5], who proved that
. A decade later, this result was extended by Bollobás [5], who proved that , for all
, for all .
.
General graphs H were only considered recently by Pikhurko and Sousa [6]. In Section 2 we will present known results about the exact value of the function  for some special graphs H and its asymptotic value for arbitrary H. In Sections 3 and 4 two new H-decomposition problems will be introduced, namely the weighted version and the monochromatic version respectively.
for some special graphs H and its asymptotic value for arbitrary H. In Sections 3 and 4 two new H-decomposition problems will be introduced, namely the weighted version and the monochromatic version respectively.
2. H-Decompositions of Graphs
In 1966, Erdös, Goodman and Pósa [4], who were motivated by the problem of representing graphs by set intersections, proved that 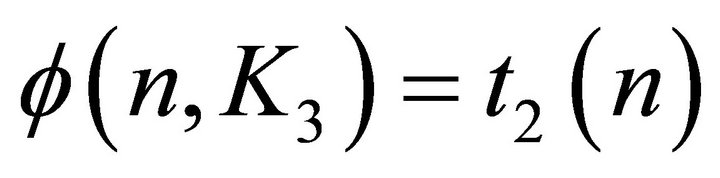 and a decade later Bollobás [5] proved that
and a decade later Bollobás [5] proved that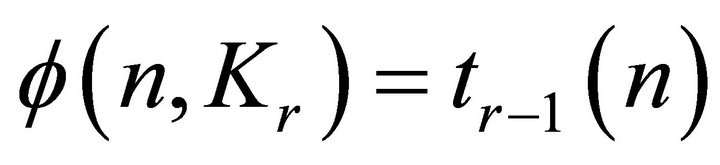 for all
for all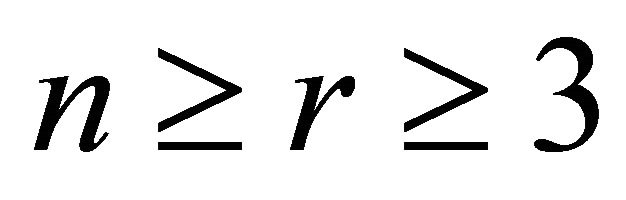 . Recently, Pikhurko and Sousa [6] studied the function
. Recently, Pikhurko and Sousa [6] studied the function 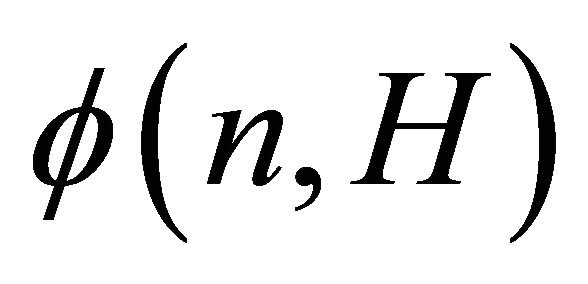 for arbitrary graphs H. They proved the following result.
for arbitrary graphs H. They proved the following result.
Theorem 2.1. [6] Let H be any fixed graph with chromatic number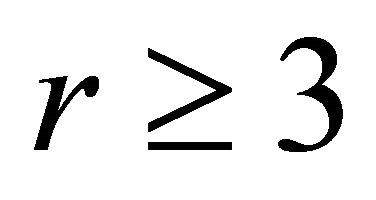 . Then,
. Then,
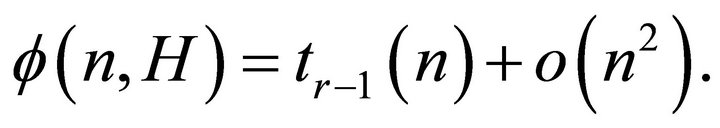
Let 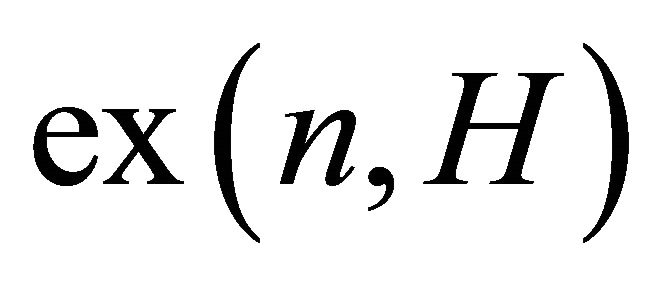 denote the maximum number of edges in a graph of order n, that does not contain H as a subgraph. Recall that
denote the maximum number of edges in a graph of order n, that does not contain H as a subgraph. Recall that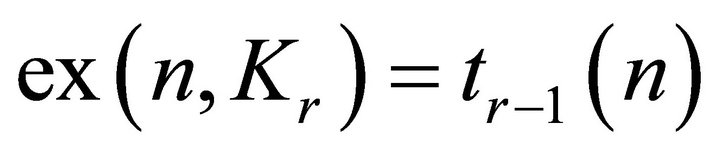 . The same authors also made the following conjecture.
. The same authors also made the following conjecture.
Conjecture 2.2. For any graph H with chromatic number at least 3, there is 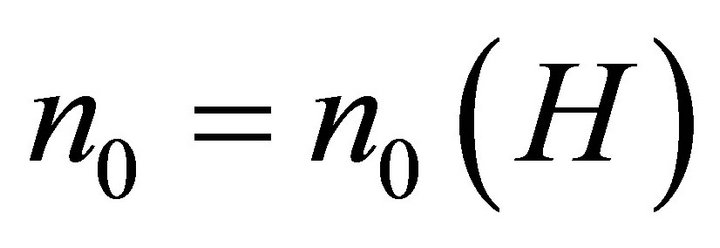 such that
such that 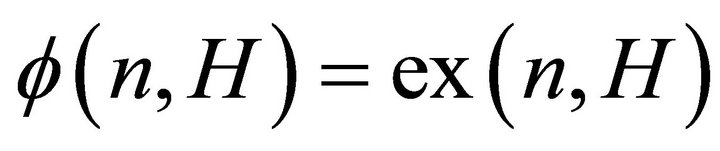 for all
for all .
.
The exact value of the function  is far from being known, however, this conjecture has been verified for some special graphs. The following results have been proved by Sousa.
is far from being known, however, this conjecture has been verified for some special graphs. The following results have been proved by Sousa.
Theorem 2.3. [7] For all 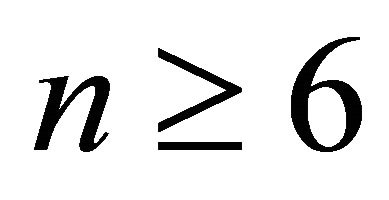 we have
we have
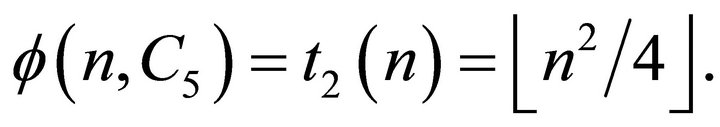
Theorem 2.4. [8] For all 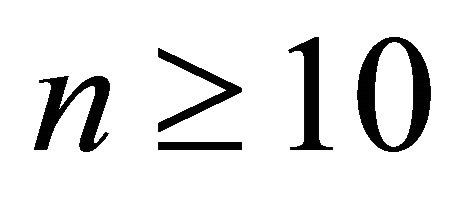 we have
we have
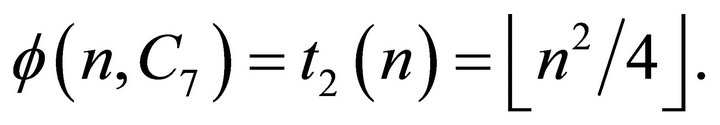
For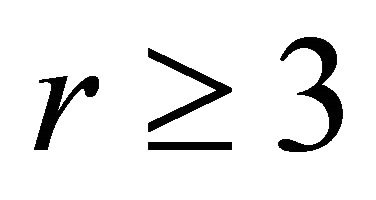 , a clique-extension of order
, a clique-extension of order 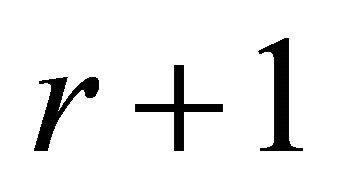 is a connected graph that consists of a
is a connected graph that consists of a  plus another vertex, say x, adjacent to at most
plus another vertex, say x, adjacent to at most  vertices of
vertices of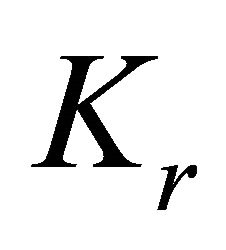 . For
. For  the
the 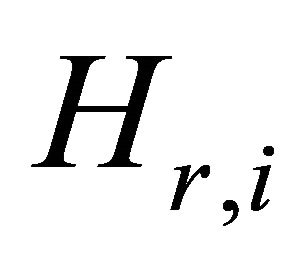 be the clique-extension of order
be the clique-extension of order 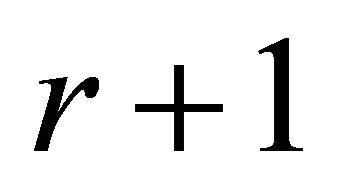 that has
that has .
.
Theorem 2.5. [9] For all 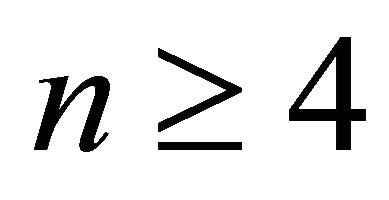 and
and  we have
we have
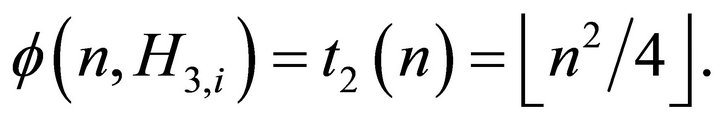
Theorem 2.6. [9] Let 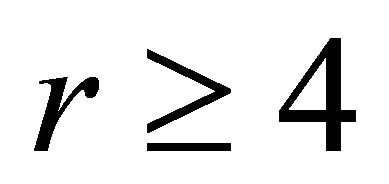 and let
and let  be any cliqueextension of order
be any cliqueextension of order . For all
. For all 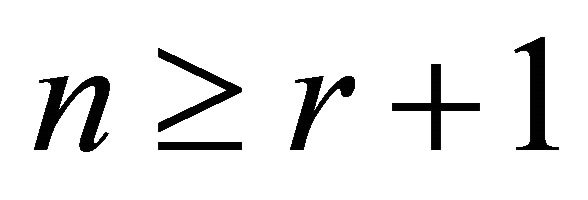 we have
we have
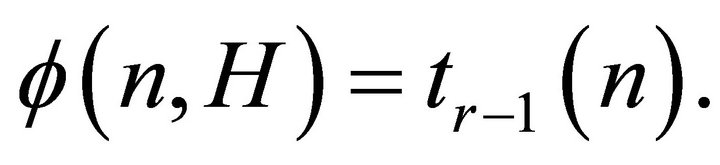
A graph H is said to be edge-critical if there exists an edge 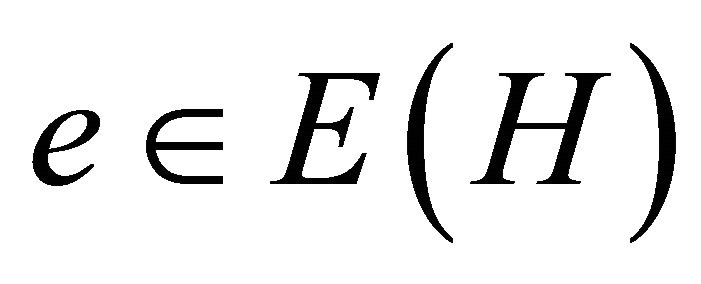 whose deletion decreases the chromatic number, that is,
whose deletion decreases the chromatic number, that is,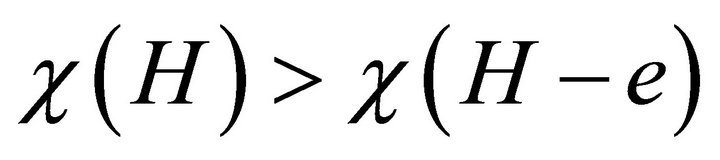 . Cliques and oddcycles are examples of edge-critical graphs. Özkahya and Person [10] were able to prove that Pikhurko and Sousa’s conjecture is true for all edge-critical graphs. Their result is the following.
. Cliques and oddcycles are examples of edge-critical graphs. Özkahya and Person [10] were able to prove that Pikhurko and Sousa’s conjecture is true for all edge-critical graphs. Their result is the following.
Theorem 2.7. [10] Let H be any edge-critical graph with chromatic number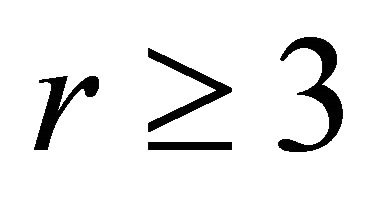 . Then, there exists
. Then, there exists 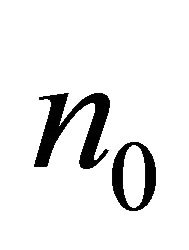 such that
such that , for all
, for all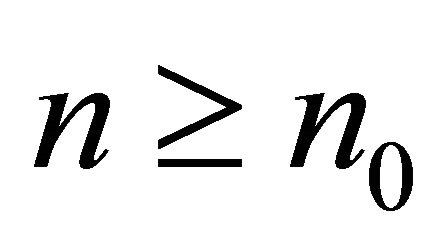 . Moreover, the only graph attaining
. Moreover, the only graph attaining 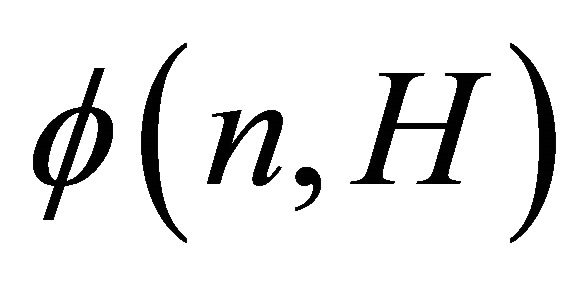 is the Turán graph
is the Turán graph .
.
The case when H is a bipartite graph has been less studied. Pikhurko and Sousa [6] determined 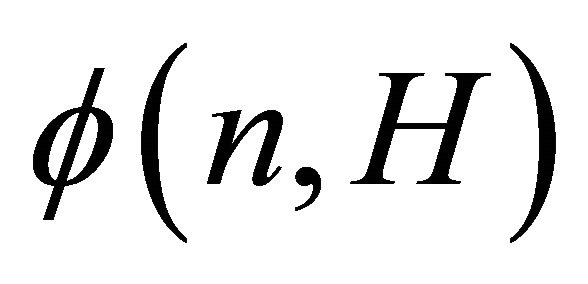 for any fixed bipartite graph with an
for any fixed bipartite graph with an 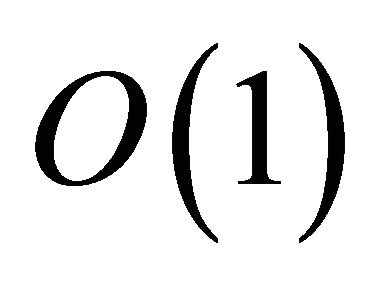 additive error. For a non-empty graph H, let
additive error. For a non-empty graph H, let  denote the greatest common divisor of the degrees of H. For example,
denote the greatest common divisor of the degrees of H. For example, 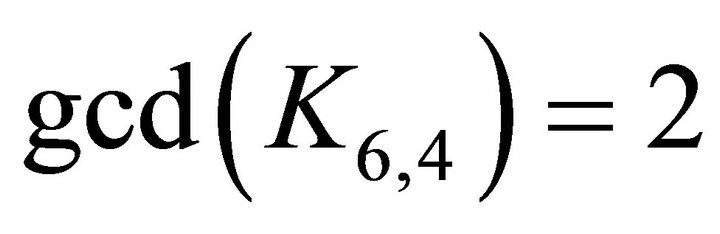 , while for any tree T with at least 2 vertices we have
, while for any tree T with at least 2 vertices we have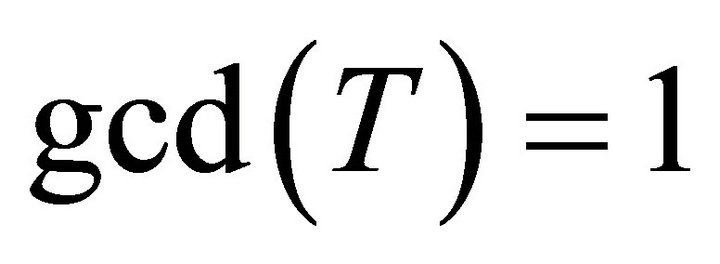 . They proved the following result.
. They proved the following result.
Theorem 2.8. [6] Let H be a bipartite graph with  edges and let
edges and let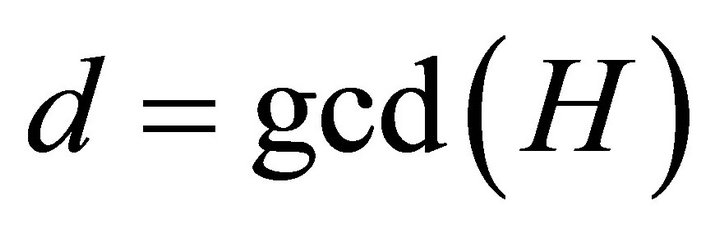 . Then there is
. Then there is 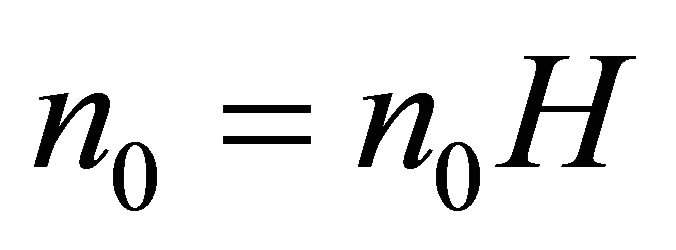 such that for all
such that for all 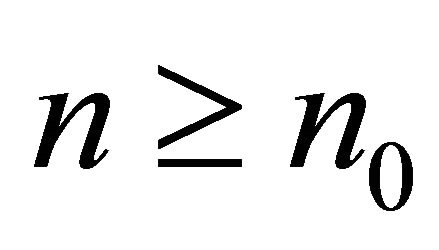 the following statements hold.
the following statements hold.
If , then if
, then if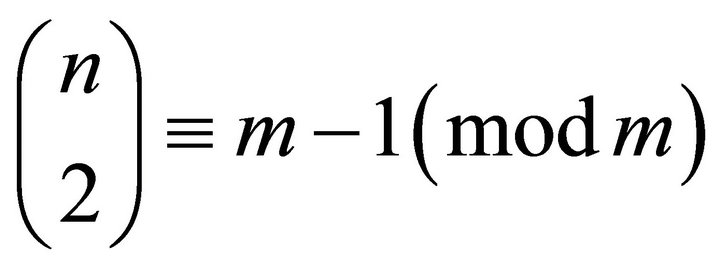 ,
,
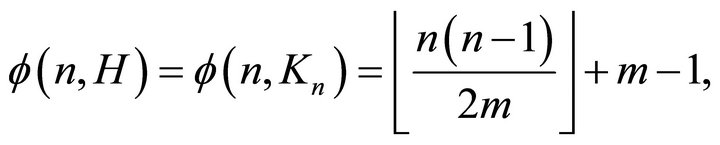
otherwise,

where 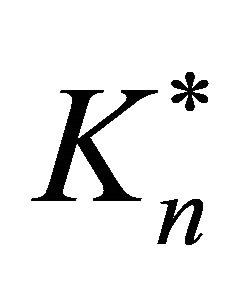 denotes any graph obtained from
denotes any graph obtained from 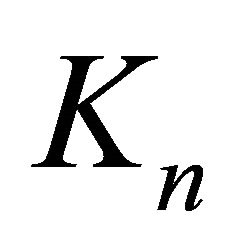 after deleting at most
after deleting at most 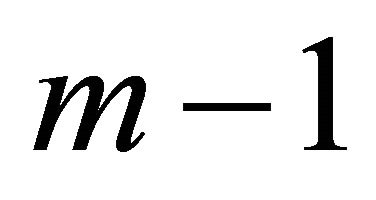 edges in order to have
edges in order to have
 . Furthermore, if
. Furthermore, if 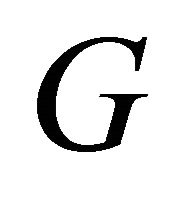 is extremal then
is extremal then  is either
is either  or
or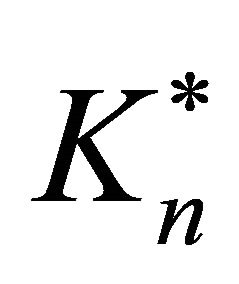 .
.
If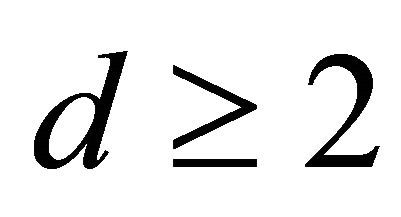 , then
, then
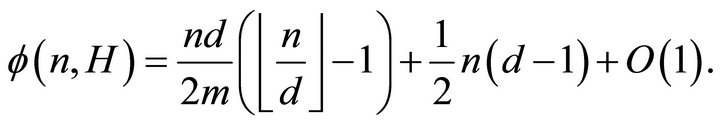
Moreover, there is a procedure with running time polynomial in 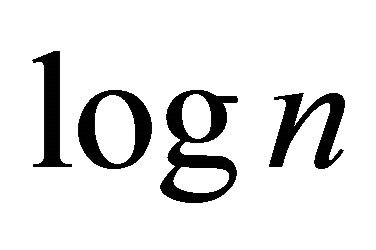 which determines
which determines 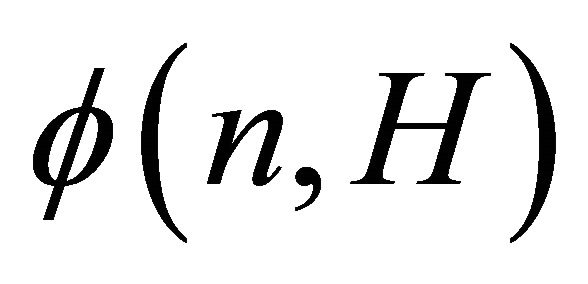 and describes a family
and describes a family  of
of 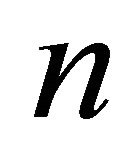 -sequences such that a graph G of order
-sequences such that a graph G of order 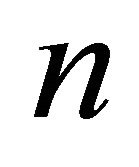 satisfies
satisfies 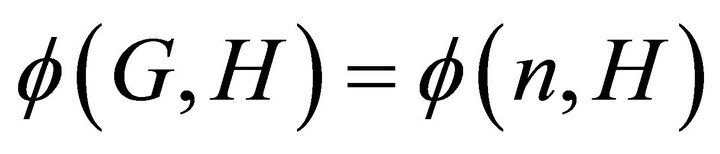 if and only if the degree sequence of G belongs to
if and only if the degree sequence of G belongs to . (It will be the case that
. (It will be the case that 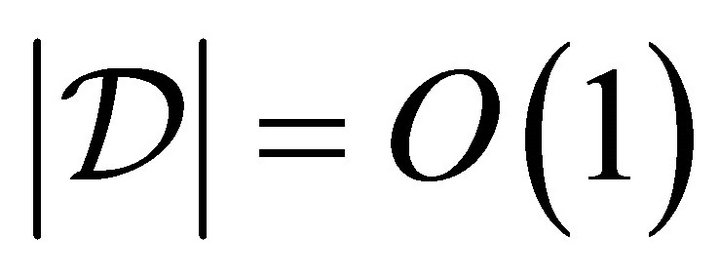 and each sequence in
and each sequence in 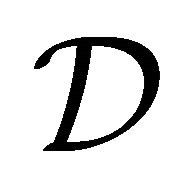 has
has 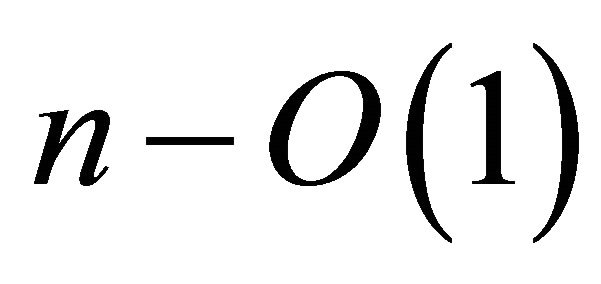 equal entries, so
equal entries, so 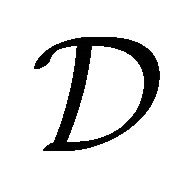 can be described using
can be described using 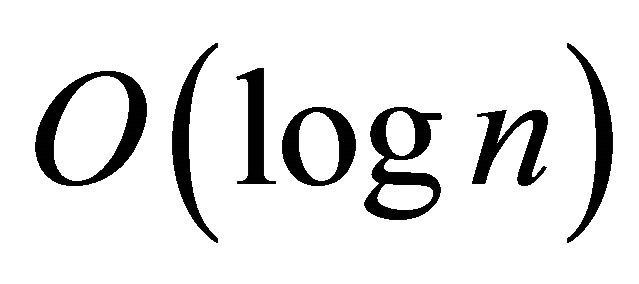 bits.)
bits.)
3. Weighted H-Decompositions of Graphs
In 2011, Sousa [11] introduced a weighted version of the H-decomposition problem for graphs. More precisely, let G and H be two graphs and b a positive number. A weighted 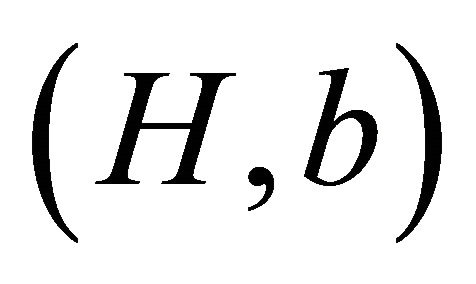 -decomposition of G is a partition of the edge set of G such that each part is either a single edge or forms an H-subgraph, i.e., a graph isomorphic to H. We assign a weight of b to each H-subgraph in the decomposition and a weight of 1 to single edges. The total weight of the decomposition is the sum of the weights of all elements in the decomposition. Let
-decomposition of G is a partition of the edge set of G such that each part is either a single edge or forms an H-subgraph, i.e., a graph isomorphic to H. We assign a weight of b to each H-subgraph in the decomposition and a weight of 1 to single edges. The total weight of the decomposition is the sum of the weights of all elements in the decomposition. Let 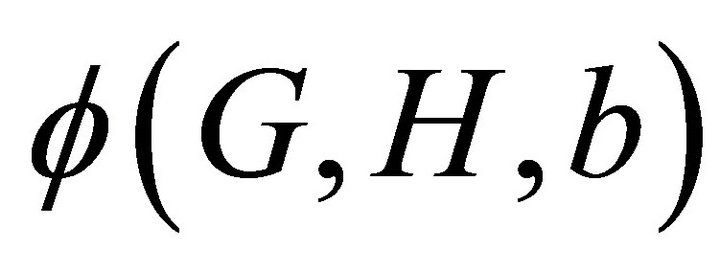 be the smallest possible weight in an
be the smallest possible weight in an 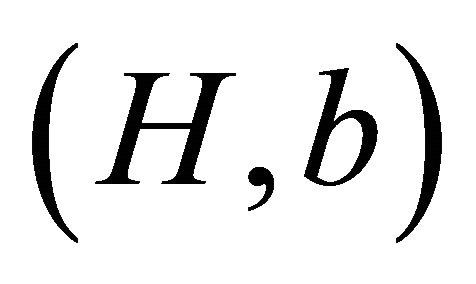 -decomposition of G.
-decomposition of G.
As before, the goal is to study the function
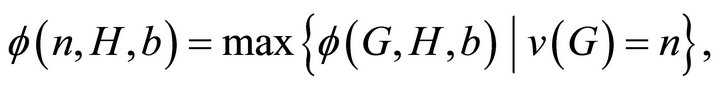
which is the smallest number such that any graph G with n vertices admits an 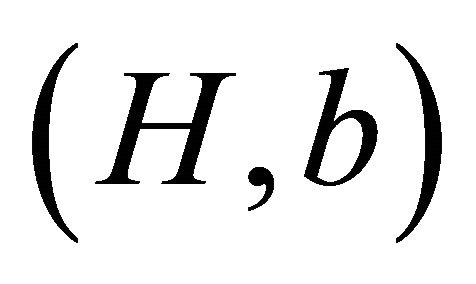 -decomposition with weight at most
-decomposition with weight at most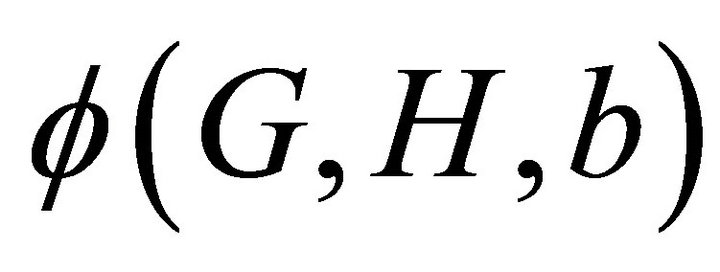 .
.
Note that when we take  the original H-decomposition problem is recovered, hence, it suffices to consider the case when
the original H-decomposition problem is recovered, hence, it suffices to consider the case when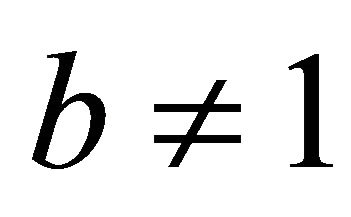 . Furthermore, when
. Furthermore, when
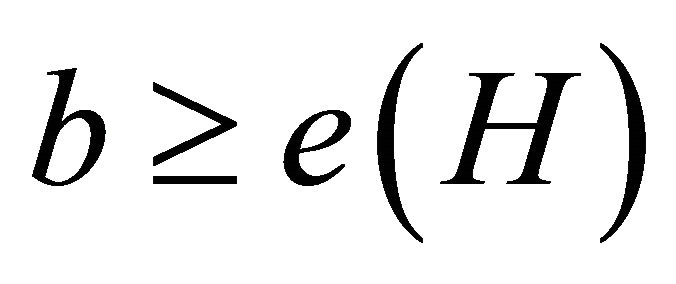 we easily have
we easily have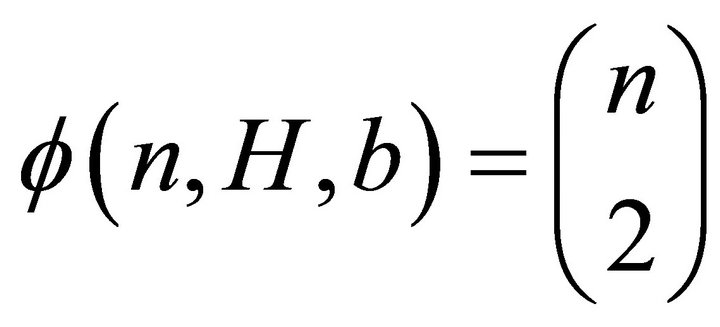 . Thereforeone only has to consider the case when
. Thereforeone only has to consider the case when 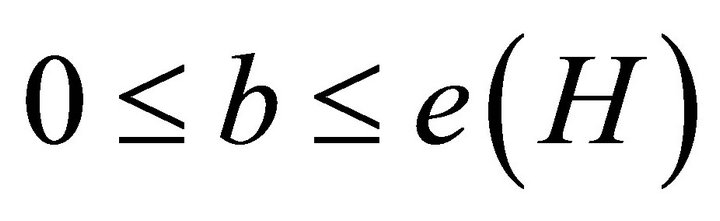 and
and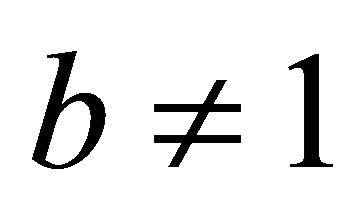 . Sousa [11] obtained the asymptotic value of the function
. Sousa [11] obtained the asymptotic value of the function  for any fixed bipartite graph H when
for any fixed bipartite graph H when 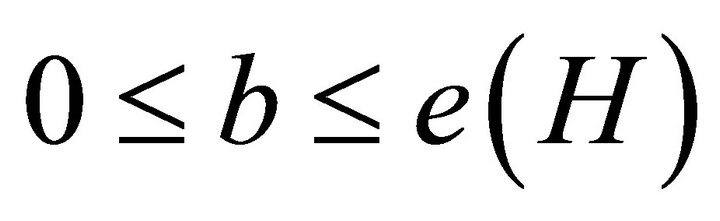 and
and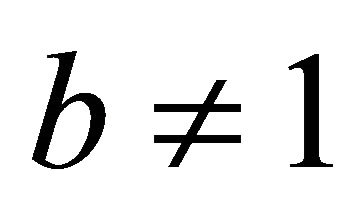 .
.
Recall that for a non-empty graph H,  denotes the greatest common divisor of the degrees of H. Sousa proved the following result.
denotes the greatest common divisor of the degrees of H. Sousa proved the following result.
Theorem 3.1. [11] Let H be a bipartite graph with 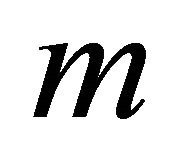 edges, let
edges, let 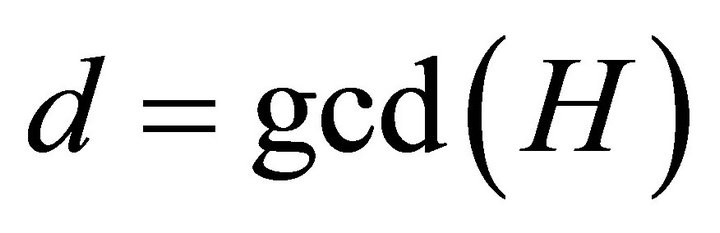 and
and  with
with 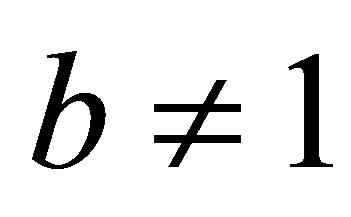 a constant. Then there is
a constant. Then there is  such that for all
such that for all  the following statements hold.
the following statements hold.
If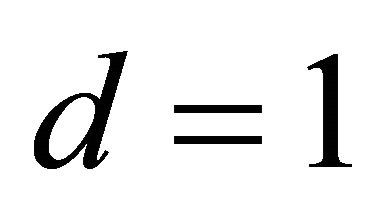 , then
, then
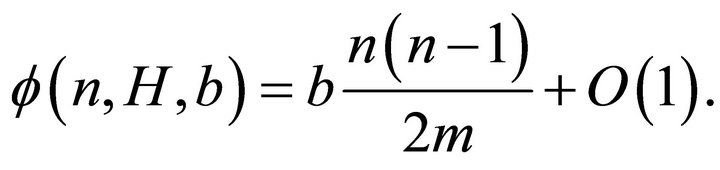
If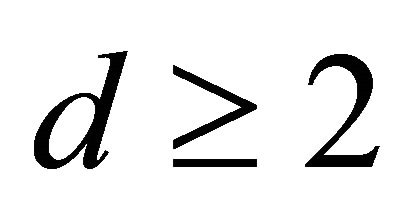 , let
, let  where
where  is an integer.
is an integer.
If  and
and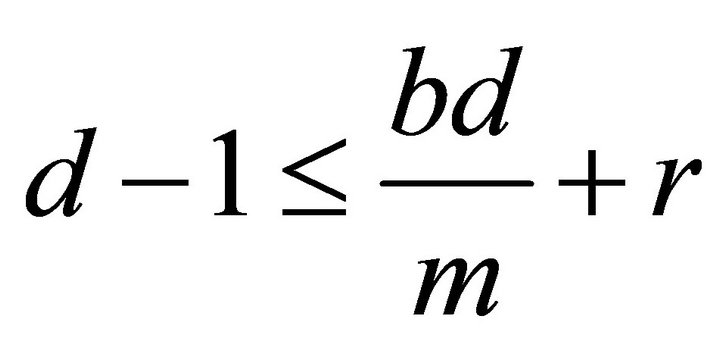 , then
, then

If  and
and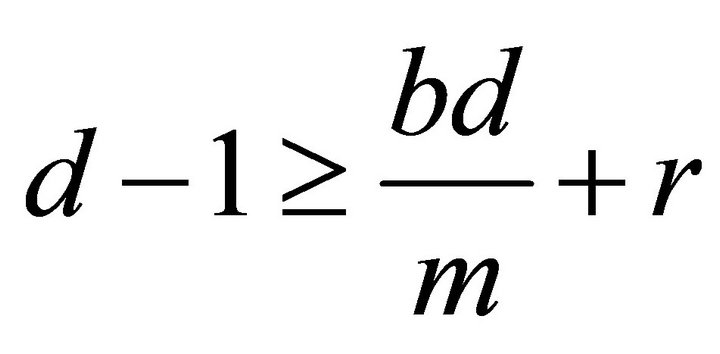 , then
, then
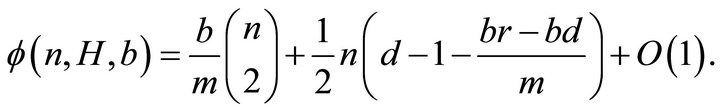
If  and
and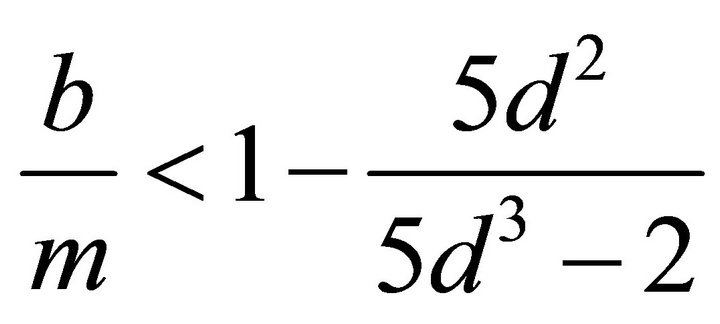 , then
, then

If 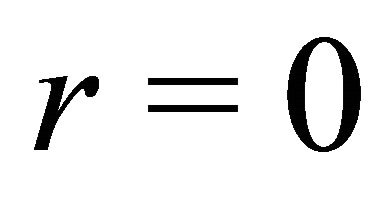 and
and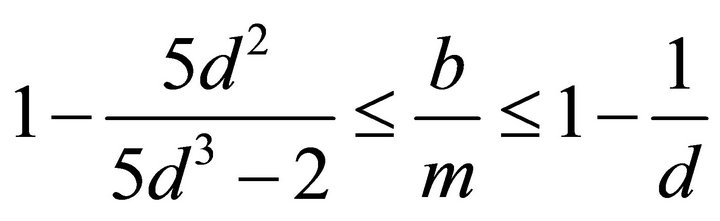 , then
, then
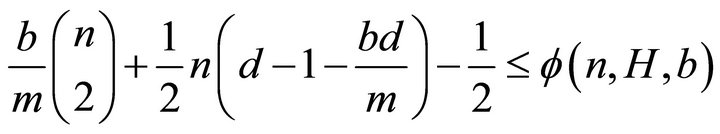
and
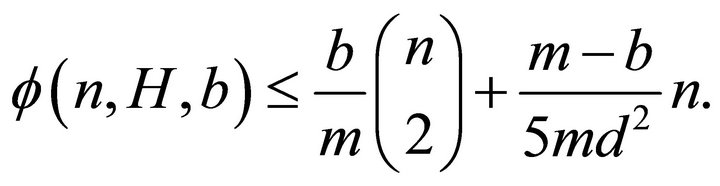
If 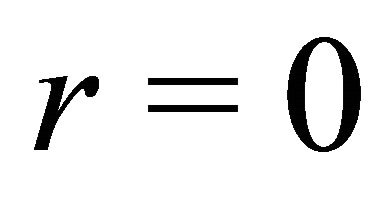 and
and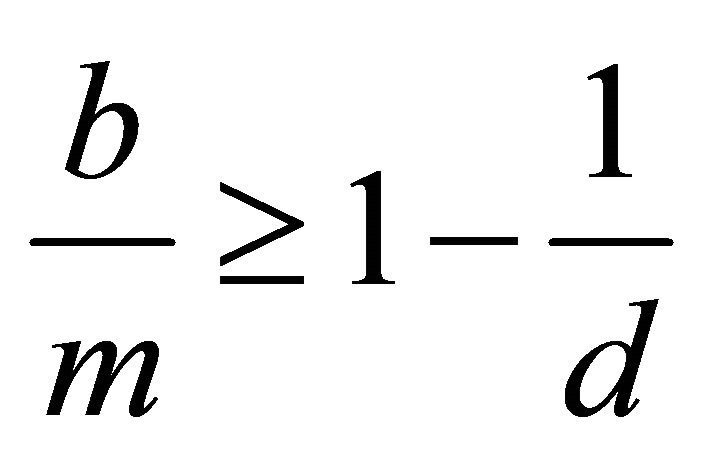 , then
, then
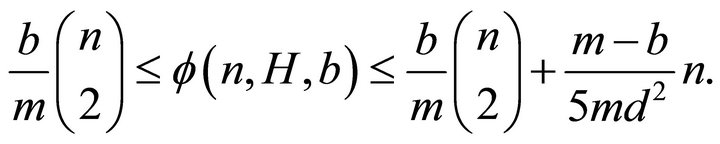
The case when H is not a bipartite graph is still an open problem.
4. Monochromatic H-Decompositions of Graphs
In this section the H-decomposition problem is extended to coloured versions of the graph G and monochromatic copies of H. We define the problem more precisely.
A k-edge-colouring of a graph G is a function . We think of c as a colouring of the edges of G, where each edge is given one of k possible colours. Given a fixed graph H, a graph G of order n and a k-edge-colouring of the edges of G, a monochromatic H-decomposition of G is a partition of the edge set of G such that each part is either a single edge or a monochromatic copy of H. Let
. We think of c as a colouring of the edges of G, where each edge is given one of k possible colours. Given a fixed graph H, a graph G of order n and a k-edge-colouring of the edges of G, a monochromatic H-decomposition of G is a partition of the edge set of G such that each part is either a single edge or a monochromatic copy of H. Let 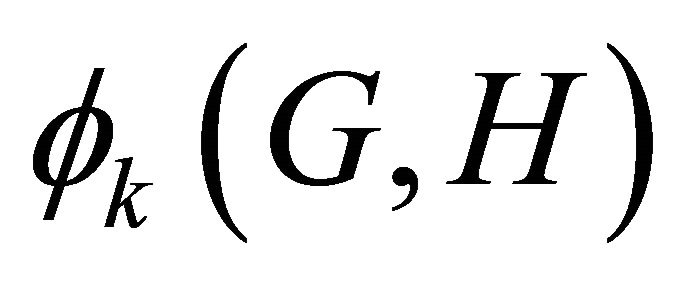 be the smallest number such that, for any k -edge-colouring of G, there exists a monochromatic H-decomposition of G with at most
be the smallest number such that, for any k -edge-colouring of G, there exists a monochromatic H-decomposition of G with at most  elements. The objective is to study the function
elements. The objective is to study the function 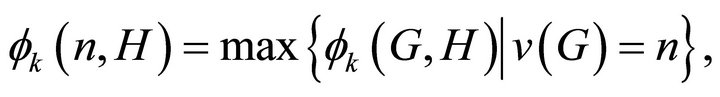 which is the smallest number such that, any k-edgecoloured graph of order n admits a monochromatic H-decomposition with at most
which is the smallest number such that, any k-edgecoloured graph of order n admits a monochromatic H-decomposition with at most 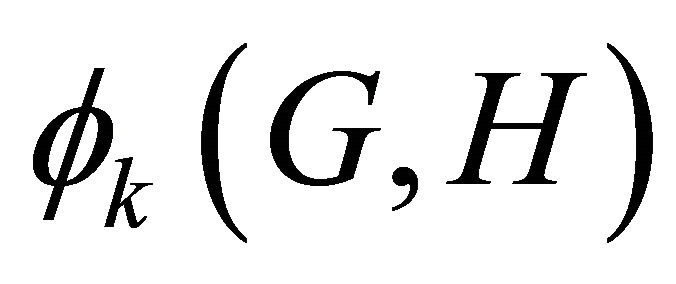 elements.
elements.
This function was introduced recently by Liu and Sousa [12] and they studied the function 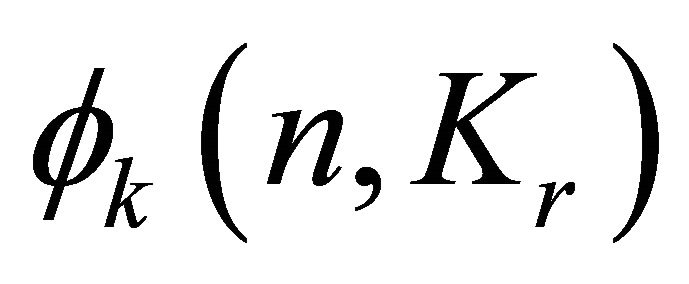 for all
for all 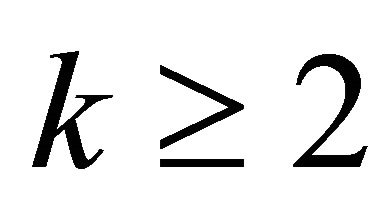 and
and . Their results involve the Ramsey numbers and the Turán numbers. Recall that for
. Their results involve the Ramsey numbers and the Turán numbers. Recall that for 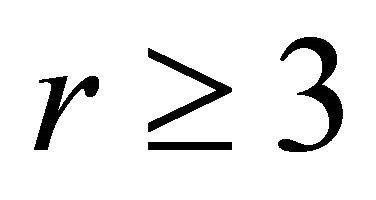 and
and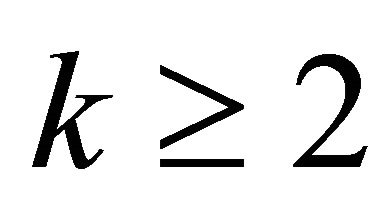 , the Ramsey number for
, the Ramsey number for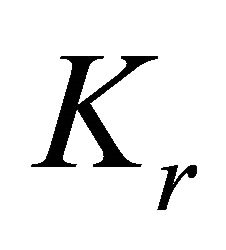 , denoted by
, denoted by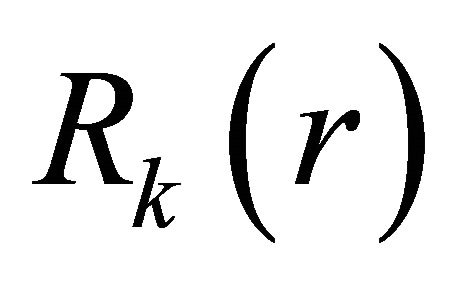 , is the smallest value of s, for which every k-edge-colouring of
, is the smallest value of s, for which every k-edge-colouring of 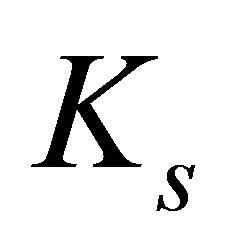 contains a monochromatic
contains a monochromatic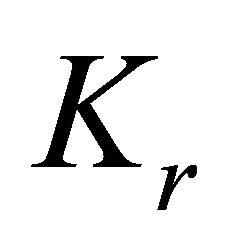 . The Ramsey numbers are notoriously difficult to calculate, even though, it is known that their values are finite for all
. The Ramsey numbers are notoriously difficult to calculate, even though, it is known that their values are finite for all  and
and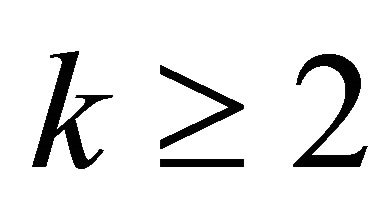 . In fact, for the Ramsey numbers
. In fact, for the Ramsey numbers , only three of them are currently known. In 1955, Greenwood and Gleason [13] were the first to determine
, only three of them are currently known. In 1955, Greenwood and Gleason [13] were the first to determine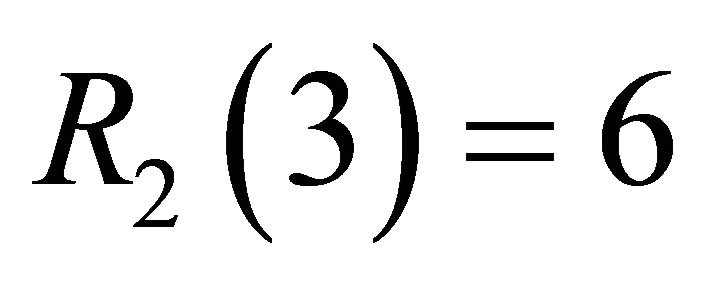 ,
,  and
and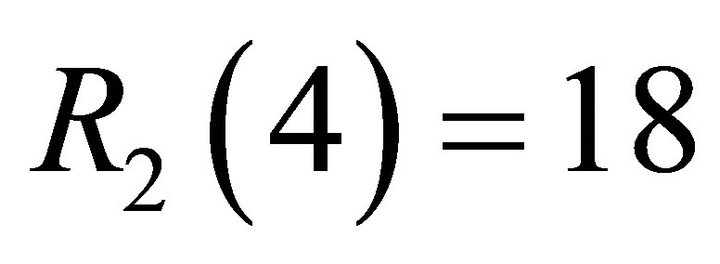 . Liu and Sousa [12] proved the following results about monochromatic
. Liu and Sousa [12] proved the following results about monochromatic 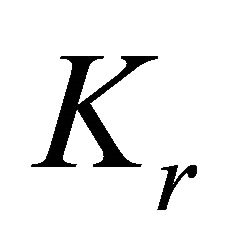 -decompositions.
-decompositions.
Theorem 4.1. [12] Let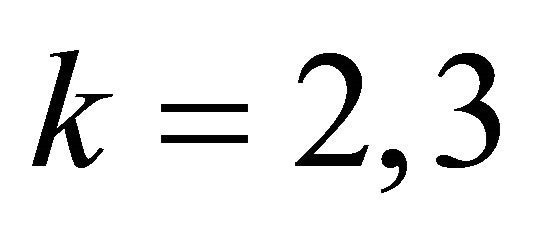 . There is an
. There is an 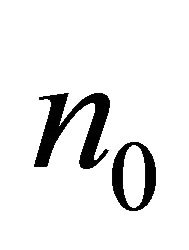 such that, for all
such that, for all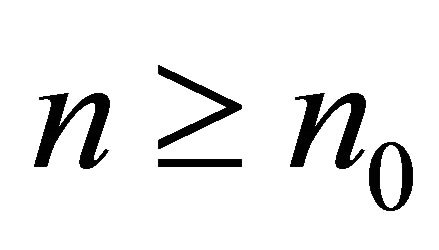 , we have
, we have
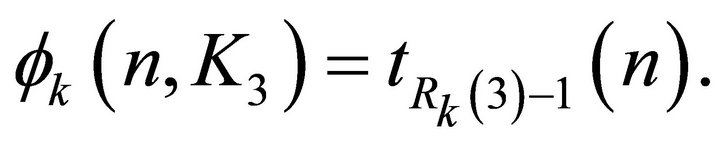
That is, 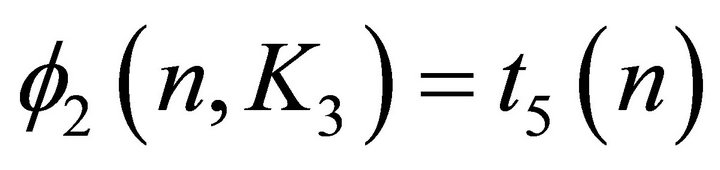 and
and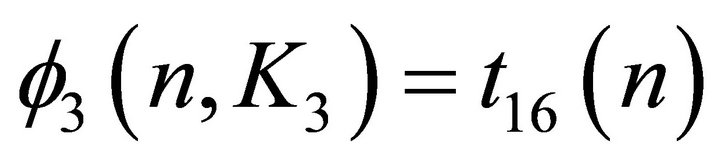 . Moreover, the only k-edge-coloured graph G attaining
. Moreover, the only k-edge-coloured graph G attaining
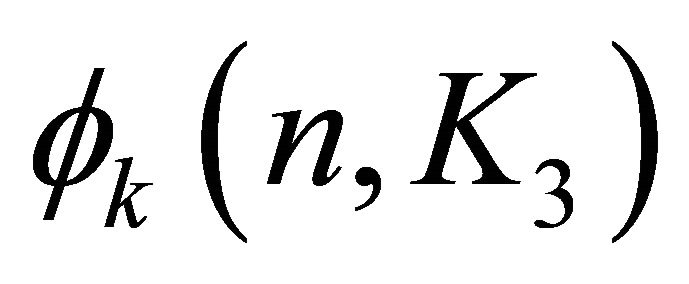 is the Turán graph
is the Turán graph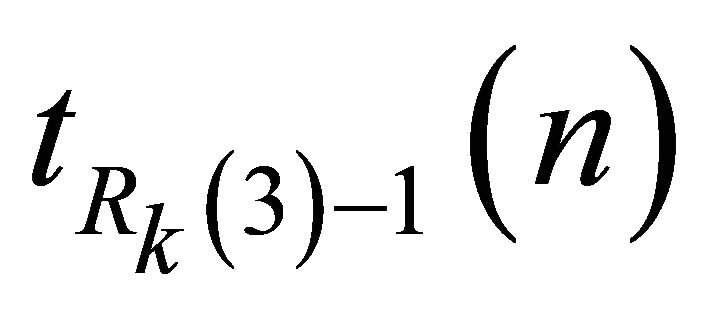 .
.
Theorem 4.2. [12] For all  we have
we have
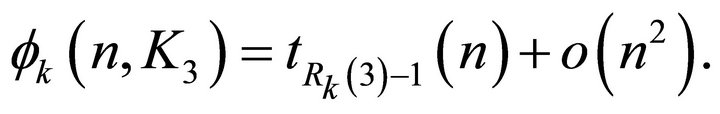
The same authors also made the following conjecture.
Conjecture 4.3. Let k ≥ 4. Then 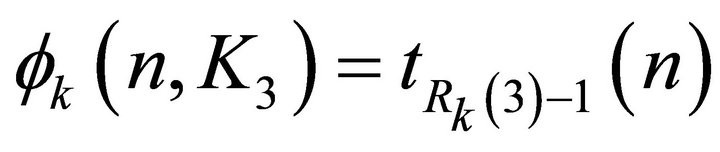 for
for .
.
Larger cliques were also studied by Liu and Sousa and they obtained the exact value of the function 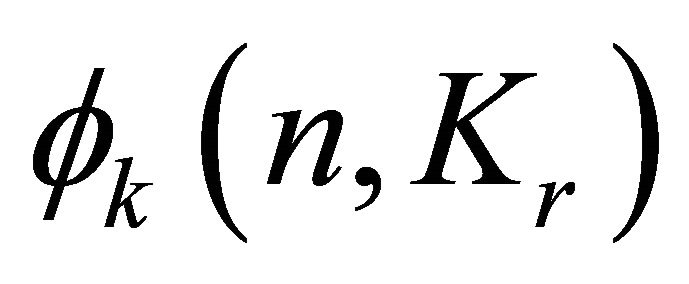 for all
for all  and
and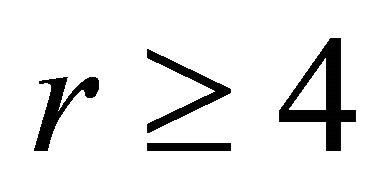 . Recall that the Ramsey number
. Recall that the Ramsey number 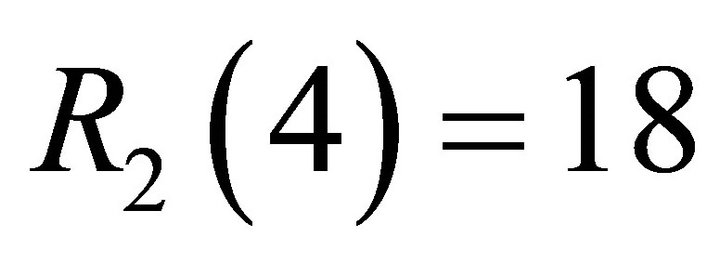 is also well-known.
is also well-known.
Theorem 4.4. [12] Let ,
,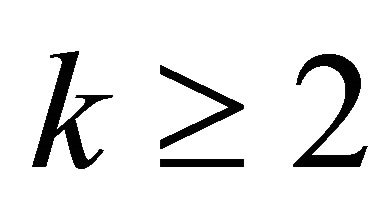 . There is an
. There is an  such that, for all
such that, for all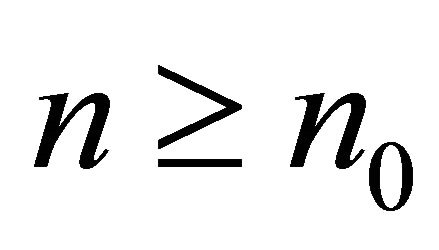 , we have
, we have

In particular,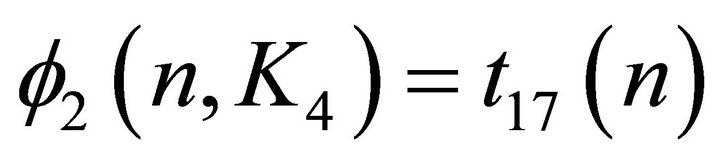 . Moreover, the only graph attaining
. Moreover, the only graph attaining  is the Turán graph
is the Turán graph
 .
.
5. Acknowledgements
The author acknowledges the support from FCT—Fundação para a Ciência e a Tecnologia (Portugal), through the Projects PTDC/MAT/113207/2009 and PEst-OE/ MAT/UI0297/2011 (CMA).
REFERENCES
- B. Bollobás, “Modern Graph Theory,” Springer-Verlag, New York, 1998. doi:10.1007/978-1-4612-0619-4
- P. Turán, “On an Extremal Problem in Graph Theory,” Matematikai és Fisikai Lapok, Vol. 48, 1941, pp. 436-452.
- D. Dor and M. Tarsi, “Graph Decomposition Is NPComplete: A Complete Proof of Holyer’s Conjecture,” SIAM Journal on Computing, Vol. 26, No. 4, 1997, pp. 1166-1187. doi:10.1137/S0097539792229507
- P. Erdös, A. W. Goodman and L. Pósa, “The Representation of a Graph by Set Intersections,” Canadian Journal of Mathematics, Vol. 18, 1966, pp. 106-112. doi:10.4153/CJM-1966-014-3
- B. Bollobás, “On Complete Subgraphs of Different Orders,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 79, No. 1, 1976, pp. 19-24. doi:10.1017/S0305004100052063
- O. Pikhurko and T. Sousa, “Minimum H-Decompositions of Graphs,” Journal of Combinatorial Theory, Series B, Vol. 97, No. 6, 2007, pp. 1041-1055. doi:10.1016/j.jctb.2007.03.002
- T. Sousa, “Decompositions of Graphs into 5-Cycles and Other Small Graphs,” Electronic Journal of Combinatorics, Vol. 12, No. R49, 2005, 7 pp.
- T. Sousa, “Decompositions of Graphs into Cycles of Length Seven and Single Edges,” ARS Combinatoria, in Press.
- T. Sousa, “Decompositions of Graphs into a Given Clique-Extension,” ARS Combinatoria, Vol. 100, 2011, pp. 465-472.
- L. Özkahya and Y. Person, “Minimum H-Decompositions of Graphs: Edge-Critical Case,” Journal of Combinatorial Theory, Series B, Vol. 102, No. 3, 2012, pp. 715-725. doi:10.1016/j.jctb.2011.10.004
- T. Sousa. “Minimum Weight H-Decompositions of Graphs: The Bipartite Case,” Electronic Journal of Combinatorics, Vol. 18, No. 1, 2011, pp. 126-135.
- H. Liu and T. Sousa, “Monochromatic Kr-Decompositions of Graphs,” Unpublished.
- R. E. Greenwood and A. M. Gleason, “Combinatorial Relations and Chromatic Graphs,” Canadian Journal of Mathematics, Vol. 7, 1955, pp. 1-7. doi:10.4153/CJM-1955-001-4

