Journal of Modern Physics
Vol.07 No.12(2016), Article ID:70246,9 pages
10.4236/jmp.2016.712145
The Hubble Field vs Dark Energy
Juan Lartigue
Department of Nuclear Chemistry, Faculty of Chemistry, National University of México, México City, México

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 June 2016; accepted 28 August 2016; published 31 August 2016
ABSTRACT
The Hubble equation was considered valid enough to calculate the recession velocity of galaxies, until further observations showed that there would be an accelerated recession in the Hubble flow, necessarily tied to an accelerated expansion of the Universe. So, this paper postulates the existence of a Hubble field as a possible cause for such an accelerated expansion, with some conditions: it must be a scalar field whose intensity should be a constant in respect to distance and whose Poisson equation should not be zero nor a function of mass; such field could rather be a property of the space-time. The obvious expression for acceleration should be the derivative of the Hubble equation respect to time, which gives two opposed-signs terms whose substitution by the De-Sitter equation drives to a permanent negative acceleration, similarly to that obtained by the 2nd Friedmann equation. Otherwise, the inclusion of the L term in the gravitational Einstein equation has led to a two opposed-signs terms expression, resembled to a non-published Newton equation. The negative term expresses the gravitational attraction and the positive one expresses the accelerated expansion as a L function, which usually is attributed to dark energy. In this paper it is shown that L is proportional to the squared Hubble parameter and that the uncertain dark energy may be substituted by the calculable Hubble field intensity to obtain an equation for the net Universe acceleration. Equations for the Hubble parameter as functions of time and radius are also deduced. A relation is shown between the various assumed masses of the Universe and its critical radius. Additional Universe parameters are estimated such as the deceleration factor and a solution for the Poisson equation in the Hubble field. A brief comment t on high-standard candles is included.
Keywords:
Hubble Law, Hubble Field, Cosmological Constant, Friedmann Equations

1. Introduction
Since the A. Riess et al. [1] discovery of the acceleration of the Universe expansion, the cause of this phenomenon has been attributed to a mysterious dark energy whose nature and characteristics remain unknown. Dark energy has been associated to the cosmological constant, L, which was previously discarded by Einstein and now is related to dark energy density, rL, as
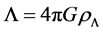 . (1.1)
. (1.1)
The dark energy presents two problems. The first one is that such alleged energy has not been detected or measured experimentally. The second one is that its density is usually expressed as an equivalent mass density (kg∙m−3) though a so-crucial relationship such as
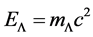 (1.2)
(1.2)
has not been proved yet. Its present numerical value has been estimated from the WMAP experiments [2] to a figure that t allows the Universe to reach its critical condition at the present time. Its hypothetical value is expressed by reference [3] as: “Dark energy is necessary to balance the books”.
Besides, there is a problematic complement of dark energy theory: it is assumed that it generates a negative pressure or vacuum energy that pulls the Universe to expand itself. Though the equation of state is feasible
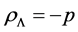 , (1.3)
, (1.3)
where −p is the negative pressure generate d) the implied numerical values would not be big enough to pull the entire Universe back. Reference [4] expresses on both topics: “The relevant fact about dark energy is not its pressure: it is that it is persistent; it doesn’t dilute away as the Universe expands”. And adds: “Banning negative pressure from popular expositions of Cosmology would be a great step forward”.
In explaining the Universe acceleration, several alternative theories have been published based on extensions of the relativistic theory of gravity and MOND theory [5] , as well as on variations of gravitation as a function of scales [6] . This later reference mentions the possible substitution of the constant L by a scalar field. Such is the proposal of this paper, assuming a constant intensity of a scalar field. It follows a review of previous concepts.
The Hubble parameter, H(t) is defined as:
 (1.4)
(1.4)
where a is the radial Universe function, related to the distance r by the co-moving equation
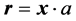 (1.5)
(1.5)
x is the constant commoving coordinate and 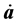 is the time derivative of a substitution of the co-moving equation in (1.1) to give the Hubble equation:
is the time derivative of a substitution of the co-moving equation in (1.1) to give the Hubble equation:
 (1.6)
(1.6)
The time derivative of this equation would represent the accelerated radial expansion:
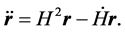 (1.6.a)
(1.6.a)
The problem here is that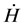 , usually obtained by the De-Sitter expression, drives to an Universe acceleration,
, usually obtained by the De-Sitter expression, drives to an Universe acceleration, 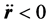 , as opposed to the present accepted criteria [7] :.
, as opposed to the present accepted criteria [7] :.
Bergstron and Goobar [8] had included the cosmological constant, L, in the Einstein gravitation equation as follows:
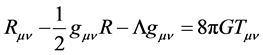 (1.7)
(1.7)
the two first terms form the Einstein tensor, Gmn; gmn stands for the fundamental covariant tensor; G is the gravitational constant, while Tmn represents the energy-momentum tensor. This expression assumes a unitary value for light velocity. Einstein added Lto his equations in 1917 in order to match a static Universe concept. However, A. Friedmann did not take L into account in obtaining two basic solutions, five years later [9]
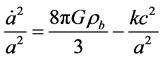 (1.8a)
(1.8a)
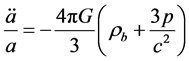 (1.9)
(1.9)
 is the acceleration of matter at the Universe radial function, a; rb is the Universe baryonic density; p is th total pressure; k is a curvature parameter of the Universe, and c is the light velocity in a vacuum. Accordingly to R. Tolman [10] , the Einstein Universe is filled by incoherent matter and, in a first Friedmann model, the total pressure is assumed to be zero, yet both energy and matter get conserved. An adequate way to fulfill Einstein and Friedmann conditions would be assuming the Universe as a powder cloud with a tiny matter density and p = 0, which implies that the energy momentum tensor [11] is
is the acceleration of matter at the Universe radial function, a; rb is the Universe baryonic density; p is th total pressure; k is a curvature parameter of the Universe, and c is the light velocity in a vacuum. Accordingly to R. Tolman [10] , the Einstein Universe is filled by incoherent matter and, in a first Friedmann model, the total pressure is assumed to be zero, yet both energy and matter get conserved. An adequate way to fulfill Einstein and Friedmann conditions would be assuming the Universe as a powder cloud with a tiny matter density and p = 0, which implies that the energy momentum tensor [11] is
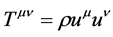 (1.9)
(1.9)
um and un are the 4-velocity vectors that, in a comoving frame, are u = (1, 0, 0, 0). Therefore, Too = rs
(When the value for L is substituted).
By applying to (1.7) the conservation criteria for matter in the Universe, plus the co-moving equation and the baryonic density concept as well, the present Universe acceleration would be:

where Mb is the baryonic (o if preferred, gravitational mass) contained in a sphere of radius r. Equation (1.8) is the same of Newton for gravitational acceleration, so implying that it remains negative as r increases, a conclusion that would result opposed to recent works [1] [12] . The first solution for Equation (1.3) was that of De-Sitter in 1917, though he did assume an empty Universe, i.e. Tmn = 0. In what follows, a L value and its relationship to the Hubble parameter are calculated. Thereafter, an equation for the Hubble field is deduced, and two equations for H as functions of time and distance are also proposed. The criticality and deceleration parameters are calculated as well as a Poisson equation for the scalar Hubble field. A brief comment on high-z standard candles is included at the end of the paper.
2. The L and H Values
By applying the FLRW metric to the Einstein equation, reference [13] gives way to a very useful form of the second Friedmann equation:

T is equation has been also deduced by L. Calder and O. Lahav in a landmark paper [14] . It can be expressed by means of the commoving equation and the density definition, as:

Since L had not been considered a function of time, reference [15] did assume a constant value for L = 1.0 (supposed it is dark energy), which should intersect the WU curve at the present time. Such a constant unitary value (assumed as vacuum energy) intersecting the WU curve at the present time is also mentioned by reference [16] . WU is the ratio between the Universe total density and its own critical density. These and other authors [2] conclude that the present time is the critical one, an assumption that would imply now that
Calder and Lahav [17] have referred an original Newton equation for the Universe acceleration (not public shed by Newton in his Principia) which may be written as:

where C is an arbitrary constant. By comparing Equations ((2.2) and (2.3)), they conclude that L must be proportional to the entire mass of the Universe, Mb (a constant) as:

However, the constancy of L would require C to be a true constant. It may be calculated at the equilibrium point (

Equating the expressions for C from (2.4) and (2.5) it gives:

So showing that L is a constant being related to the critical radius. Otherwise, the equation presented by reference [8] and anywhere (L = 8pGrL) would require knowing the dark energy density, an uncertain parameter at the present time.
The proposition of M. Carmeli and T. Kuzmenko [18] for theL constant value could be a real solution:

to is the age of the Universe; if it is to = 14.0 × 109 (y) [19] , then L = 1.53 × 10−35 (s−2) [19] .
Accordingly to Equation (1.1) the Hubble parameter is a function of time. Its present (constant) value, Ho is defined as:

Therefore, from (2.7) and (2.8):

Multiplying Equation (2.9) by ro gives:

If this equation is valid at the present time, it is postulated in this work to be valid also at the critical time, i.e.

and therefore, at any time:

Equation (2.10) shows that the second term of Equation (2.2) does imply a positive acceleration expansion, with a constant value as proposed by reference [4] , and opposed to the gravitational attraction in the Universe. So, if Equation (2.12) is valid, the Equation (2.2) may be written as:

Equation (2.13) represents the net acceleration of the Universe expansion, i.e., the difference between the attractive gravitational field and the expansive Hubble field. It seems clear that, when the Universe radius was small, the gravitational field intensity was dominant, but nowadays, at a bigger Universe radius, the Hubble field intensity should be overbearing, as shown in Figure 1.
3. The Hubble Field
In what follows, the variable intensity of the gravitational field is represented by G and the constant intensity of the Hubble field is written as ГH, i.e.


Therefore, the net Universe acceleration may be expressed, from Equation (2.13), as the difference:
Figure 1. The constant Hubble field intensity GH (m∙s−2, red line) vs 3 cases of gravitational acceleration GG (m∙s−2, blue, green, purple lines, see text) as functions of the Universe ratio, r/ro. The intersection points correspond to the 3 possible critical Universe radii. The critical times are marked in the upper abscissa. The difference between the GG lines and the GH line represents the net acceleration, 

Since the potential energy in the gravitational field is always negative (U < 0), the gravitational potential (energy per unit mass) is negative too; it is expressed as:

By definition [20] , the intensity of the gravitational field is the negative of the gradient of the gravitational potential:

it is therefore negative, as expressed in Equation (3.1).
Similarly, the Hubble field intensity could be defined as the gradient of a positive scalar Hubble field potential:

The substitution of Equation (3.2) in (3.6) gives a definition of the Hubble field intensity

By assuming from Equation (2.12) that GH = constant in Equation (3.7), the radial integration of this equation gives an expression for the Hubble potential:

(alternative units applied in Equation (3.8) point out that there is no mass involved in the Hubble potential).
Assuming that Equation (2.12) is valid, it is possible to estimate the constant Hubble field intensity by using the present values of Ho and the Universe radius, ro [21] :

This would be the value of the Hubble field intensity, i.e. the Hubble acceleration of the Universe at any time, if there was not a gravitational field. Since it is not feasible to assign to the Hubblefield any known physical entity, it may be assumed that it corresponds, rather, to a property of the space-time. The present net acceleration results, from Equation (2.13), 


The assumption for ГH to be constant allows obtain a general expression for H as a function of distance, from Equations ((2.12) and (3.9)):

The present Ho value has been defined as the reciprocal of the Universe age (Equation (2.8)) but there is not a general expression to determine H(t). The same Equations ((2.12) and (3.9)) could allow calculate the Hubble parameter at any time if the distance is expressed as a function of time in a continuously accelerated movement:

Therefore, Equations ((3.10) and (3.11)) are proposed as general functions for H(r) and H(t).
4. Additional Relevant Parameters
4.1. Critical Parameters Corresponding to the Assumed Values of Mass in the Universe
From R. Johnson [22] , the values assigned to the baryonic mass of the Universe vary according to several criteria: one is based on the total number of stars and it yields 1.0 × 1052 kg; even figure, as modified by the intergalactic and interstellar media, is 1.7 × 1053 kg; another one, based in the Hoyle-Carvalho equation [23] , assigns Mh = 1.84 × 1053 (kg) as the value covering the Hubble length (1.37 × 1026 m). All these figures have been obtained by research inside the observable Universe, i.e. into the Hubble sphere. So, accordingly to the cosmological principle, trying to determine the total mass contained in the total volume of the Universe is a valid problem. From the above given data, the density of the observable Universe is rh = 1.8 × 10−26 (kg∙m−3) a value here assumed for the entire Universe whose radius is estimated to be ro = 4.4 × 1026 (m) [2] giving, for the total baryonic mass in the Universe, Mu = 6.5 × 1054 (kg). Besides, dark mass could eventually be included as a gravitational mass, giving a total of Mg = 3.25 × 1055 (kg).
The critical point of the Universe may be defined as the time when the Universe becomes flat, i.e. when it may change from positive to a negative curvature. That implies 

In Equation (4.1) it has not been specified the kind of mass to apply, which must be selected in any case.
Since the l.h.s. is a constant (GH), it is possible to directly obtain the value of the critical radius from:

Since G and GH are constants, this equation gives

In Table 1 they are shown the corresponding critical radius and times for the three above assumed masses.
4.2. The Deceleration Parameter
The deceleration parameter, q, is defined as:

Its present value results q = −1.3, which confirms the possibility of an accelerated Universe.
4.3. The Poisson Equation
The spatial derivative of Equation (3.7) is a solution of the Poisson equation in the Hubble field:

It means that there exists a force-flow in the Hubble field.
5. A Brief Comment
As assumed above, the constancy of GH would require some kind of justification. Subsequent studies to that of Riess et al. [1] , which was limited to z ≤ 1, refer also to the present accelerated expansion of the Universe, i.e. whose velocity is continuously increasing but there is no mention about the acceleration’s magnitude, even less about any variation; so, by now, it may be assumed that the expansive acceleration value obtained by Equation (3.9) in this work is a constant, as expressed by the product H2r in Equation (2.12).
Reference [24] analyses the Universe evolution for redshifts z ≤ 3.0 and concludes, in his Figure 4, that there were two epochs: an slowing down expansion and, after that, the present accelerated expansive period; it would mean that after the enormous velocity reached in the inflationary period, it followed a slowing down expansion period that, just before the present time, with z = 0, has changed to a positively accelerated expansive process; in this way, the present time would almost correspond to the critical time with its implicit critical radius and density as well as a flat geometry (k = 0). These results do not coincide at all with those of A. Riess [25] who proposes a value of z = 0.46 for the curvature change, a value that would imply a critical time of 10.5 Gy. It was an event considered by the same author [26] as “a cosmic jerk: the transition from desceleration in the past to acceleration in the future”. A possible partial matching of Figure 1 of this work with Figure 4 of reference [24] could be that: if H is a constant respect to time and distance, the slowing down expansion period would correspond to the
Table 1. Critical radius and critical time for three cases of universe’ mass.
[GG] > GH epoch (in the total Universe case, curve sphere case, curve Gh). Consequently, the GH = [GG] step would have defined the critical time in two possible cases. If dark matter would have been added, the critical point would still have to wait for another to period. The validity of the model here proposed could only be proven if future SN observations detect additional increases in the expected distances, at several (z > 1) values, and if they match with the net acceleration given by Equation (3.3). Some important experiments at higher z values (8.6 and 11.0) have been performed in two recent projects [27] [28] that mention mag variations but say nothing about older acceleration values.
Anyway, there is a limit to distance measurements by present methods: it comes from the estimation of reference [29] about the first star formation, that he assumes to have occurred at a Universe age of~50 (My), or z ~50, a fact that puts a limit to the use of SN as standard candles. The same restriction could apply to the efforts to use quasars [30] and γ-ray bursts [31] as standard candles. However, spectroscopic methods could always been applied if higher redshifts (z > 50) could be identified; for example, the CMB defines the maximum observable cosmological value at z~103 [29] ; it implies e.g., if lo is today about 1 (mm), the emitted le should have been about 1 (mm) i.e. infrared photons traveling till now, in a co-moving coordinate, since the decoupling time.
6. Conclusions
1) The value of the cosmological constant, L is proportional to the reciprocal of the squared Universe age (Equation (2.9)). So, it results proportional to the present value of the squared Hubble parameter.
2) Since L cannot be directly associated to any known field, the present work substitutes the L term by a constant Hubble field intensity term (Equation (2.10)), to obtain the Equation (2.13), expressed in Figure 1. The form of this equation could have been foreseen from the time derivative of the Hubble Equation (1.2) which shows that the net acceleration of the Universe would depend on two opposed-signs terms.
3) The Hubble field intensity is defined as the gradient of a positive Hubble potential (Equation (3.6)). Its constant value is 2.2 × 10−9 (m∙s−2). However, the present net acceleration is 1.7 × 10−9 (m∙s−2). The expansion velocity at the astronomical radius results today
4) The assumption of the constancy of the Hubble field intensity drives to obtain two general functions of time and distance for the Hubble parameter (Equation (3.10), Equation (3.11)).
5) Equation (2.13) gives the net acceleration of the Universe, as well as its critical radius when
6) The deceleration parameter gave a negative value, so showing that the Universe is self-expanding. The Poisson equation for the Hubble field is Ñ2VH = H2, since matter is not a component of the Hubble field.
7) The validity of the model here proposed could only be proven if future SN observations detect additional increases, such as it is being assumed in a recent academic project.
Acknowledgements
Author thanks to Sc. M. M. A. Zúñiga, C.P. V.M. Torres Tovar, D. Camargo, B. M. Cota and R. Cervantes, by their kind collaboration in the final version of this paper.
Cite this paper
Juan Lartigue, (2016) The Hubble Field vs Dark Energy. Journal of Modern Physics,07,1607-1615. doi: 10.4236/jmp.2016.712145
References
- 1. Riess, A., et al. (1998) The Astronomical Journal, 116, 1009-1038.
http://dx.doi.org/10.1086/300499 - 2. NASA/WMAP Science Team (2014)
http://map.gsfc/nasa.gov/universe/uni_matter - 3. Freedman, W.L. and Turner, M.S. (2003) Reviews of Modern Physics, 75, 1446.
http://dx.doi.org/10.1103/RevModPhys.75.1433 - 4. Carroll, S. (2013) Why Does Dark Energy Make the Universe Accelerate?
www.preposterousuniverse.com/blog - 5. Mendoza, S. (2015) Canadian Journal of Physics, 93, 217-231.
http://dx.doi.org/10.1139/cjp-2014-0208 - 6. Capotziello, S., et al. (2009) A Bird’s Eye of f(R) Gravity. arXiv: 0909.4672v2.
- 7. Lidsey, J.E. (2014) Cosmology Course ASTM108/PHY7010U, eq. (2.7), School of Physics and Astronomy, Queen Mary, University of London.
- 8. Bergström, L. and Goobar, A. (2004) Cosmology and Particle Astrophysics. 2nd Edition, Springer, Berlin.
- 9. Lidsey, J.E. (2014) Cosmology Course ASTM108/PHY7010U, eq. (2.27) and (2.29).
- 10. Tolman, R. (1958) Relativity, Thermodynamics and Cosmology. Oxford-Clarendon Press, p. 344,
- 11. Terzic, B. (2008) Astrophysics Course Phys. 652, eq.(50), NICADD, Northern Illinois University.
- 12. Sartori, L. (1996) Understanding Relativity, Fig. 9.1. University of California Press, Oakland.
- 13. Bergström, L. and Goobar, A. (2004) Cosmology and Particle Astrophysics eq. (4.97). 2nd Edition, Springer, Berlin.
- 14. Calder, L. and Lahav, O. (2008) Dark Energy: Back to Newton? invited conference in Reference .
- 15. Terzic, B. (2008) Astrophysics Course Phys. 652, Appendix to Lecture 6, Fig. 17.
- 16. Taylor, E.F., Wheeler, J.A. and Bertschinger, E. (2009) Exploring Black Holes: Introduction to General Relativity. Chapter 19, Figure 1, Draft of the 2nd Edition, Pearson Addison Wesley, San Francisco.
- 17. Calder, L. and Lahav, O. (2008) Dark Energy: Back to Newton? Invited Conference in Reference
- 18. Carmeli, M. and Kuzmenko, T. (2001) Value of the Cosmological Constant: Theory versus Experiment. Arxiv: astro-ph0102033, eq. (5).
- 19. Lidsey, J.E. (2014) Cosmology Course ASTM108/PHY7010U. Figure 6.5.
- 20. Lindsey, R.B. and Margenau, H. (1957) Foundations of Physics. Dover Publications, 284.
- 21. Sartori, L. (1996) Understanding Relativity. University of California Press, Berkeley, eq. 9.29.
- 22. Johnson, J.R. (2013) Comprehending the Cosmos: A Macro View of the Universe. 2nd Edition, CreateSpace Independent Publishing Platform, 264-294.
- 23. Valev, D. (2012) Estimation of the Total Mass and Energy in the Universe. 2010arXiv1004-1035.
- 24. Perlmutter, S. (2003) Physics Today, 53-60.
http://dx.doi.org/10.1063/1.1580050 - 25. Riess, A., et al. (2004) Astrophysical Journal, 607, 665-687.
http://dx.doi.org/10.1086/383612 - 26. Riess, A., et al. (2007) Astrophysical Journal, 659, 98-121.
http://dx.doi.org/10.1086/510378 - 27. Lehnert, M.D., et al. (2010) Nature, 467, 940-942.
http://dx.doi.org/10.1038/nature09462 - 28. Coe, D., et al. (2012) Astrophysical Journal, 762, 1-23. arxiv 1211.3663.
- 29. Goodstein, D. (2011) Adventures in Cosmology. Figure 3.2, World Scientific, Singapore.
- 30. Dai, D.-C., et al. (2012) Physical Review Letters, 108, Article ID: 231302.
http://dx.doi.org/10.1103/PhysRevLett.108.231302 - 31. Sartori, L. (1996) Understanding Relativity. Figure 9.1, University of California Press, Berkeley.
- 32. Schaefer, B.E. (2007) Astrophysics Journal, 660, 16-46.
http://dx.doi.org/10.1086/511742



