Received 22 July 2015; accepted 24 August 2015; published 27 August 2015

ABSTRACT

This work revises and extends the author’s previous work (2015), Journal of Modern Physics, 6, 78- 87, by proposing that the index of refraction n of intergalactic space (IGS) is of electromagnetic origin. This leads to a theoretical expression for n that agrees very well with the least squares value obtained previously. A table comparing the fractional distance increase predicted by the two differently obtained indices is given. This revised view requires that the high energy charged particles found in cosmic rays originate from high energy neutral particles, presumably high energy gamma rays, that were able to travel through the IGS without energy loss due to Cherenkov radiation. An alternative explanation for the counter indication from the IceCube findings of Abassi, R., et al. (2012) Nature, 484. 351-353 is proposed, which might also explain the findings of Aartsen et al. (2013) Physical Review Letters, 111, 021103. Since the model predicts galaxies act as divergent lenses, a geometrical analysis and corresponding figure describing this effect is given, as well as a table for a range of angles to the image galaxy relative to the direction to a target galaxy that is divergently lensed. The reduction of the speed of light in the IGS leads to a revision of the Planck (2015) value of the Hubble constant of ~68 km∙s⁻¹∙Mpc⁻¹ to ~47 km∙s⁻¹∙Mpc⁻¹, and hence an age for the Einstein-de Sitter universe greater than that of the oldest white dwarfs in the Galaxy, thereby resolving a long-standing problem with this model of the universe.

Keywords:

Speed of Light, Cosmic Rays, Divergent Lensing, Hubble Constant

1. Introduction

In a previous work [1] hereafter denoted as I, it was shown that it is possible to obtain an overall several percent fit to the diminished brightness of the Type Ia Supernovae (Sne Ia) found by Perlmutter et al. [2] [3] , Riess et al. [4] , and Schmidt et al. [5] , as well as to the baryon acoustic oscillation (BAO) distances obtained by Anderson et al. [6] , under the assumption that the dark energy does not accelerate the expansion of the universe in accordance with the flat LCDM model, but rather reduces the speed of light to a value of c/n, where n is the proposed index of refraction of the dark energy, which was found by a least squares evaluation to be 1.49. It was also assumed in I that n was not of electromagnetic origin, but due to some new kind of interaction so as to avoid Cherenkov radiation losses by high energy charged particles traveling through the dark energy of intergalactic space (IGS), which would conflict with their appearance in cosmic rays. However, as will be shown in this work, this assumption is unnecessary, and instead in Section 2 it will be shown that with the assumption of neutral particles traveling through the IGS being responsible for the observed high energy charged particles in cosmic rays, it is possible to assume an electromagnetic origin of n, for which one obtains a simple mathematical relation that leads to a value of n that is in good agreement with the least squares value found in I. Some applications to cosmic rays are also proposed. In Section 3, to further test the proposed expression for n, alternative values for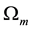, and 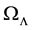are used to obtain a new least squares value for n which is in excellent agreement with the new method for obtaining n. The results are presented in Table 1. In Section 4, an astronomical prediction due to divergent lensing that was briefly described in I is described in greater detail, and a diagram illustrating the prediction under stated assumptions is given in Figure 1. Also in Table 2, the predicted angle of observation for the divergently lensed galaxy under various assumed observation angles is given. In Section 5, the issue of the ages of the white dwarfs in the globular clusters of the Galaxy as compared to the apparently shorter age of the universe for the fiducial Einstein-de Sitter universe used in I, and also here, is resolved. It is shown that the reduction in the speed of light through the dark energy of the IGS entails that the Hubble constant is smaller than its current value, which leads to a resulting age for the Einstein-de Sitter universe that is in very good agreement with that found for the accelerating universe, so that the age of the Einstein-de Sitter universe is longer than the maximum age of the white dwarfs by ~10⁹ yr. In Section 6 there are concluding remarks.

2. Cosmic Rays and Possible Electromagnetic Origin of n

As remarked above, it was assumed in I that the index of refraction n of the dark energy was not of electromagnetic origin so as to eliminate the possibility of energy loss by Cherenkov radiation by high energy charged particles traveling through the IGS, which would tend to negate their appearance in cosmic rays, in conflict with observation. However, in attempting to make a model in which n was not of electromagnetic origin, the following theoretical objection was found. Although, as is well-known, a free charged particle cannot emit a photon, since it would violate the conservation of energy and momentum, in contrast, as discussed in a quantum theory approach to the emission of a photon in the Cherenkov effect by Cox [7] , this is not the case for a “dressed” photon whose energy-momentum relation is of the form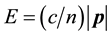. Thus, although the probability for radiation would be different than for the standard electromagnetic expression, there would be no obvious way to prevent what might be described as a “weak” Cherenkov affect. Such a radiation loss, combined with the enormous distance through the IGS which high energy charged particles would have had to travel to reach the Galaxy, would have made the high energy and ultra-high energy charged particles found in cosmic rays highly unlikely, or even impossible. Thus the non-electromagnetic model for n proposed in I is surely incorrect, and n is most likely of electromagnetic origin, and since charged particles would experience Cherenkov radiation loss, hence either: 1) the proposed alternative to the accelerating universe based on a reduced speed of light through the dark energy would be incorrect, or 2) some other explanation for the ultrahigh energy and high energy charged particles found in the cosmic rays would be involved.

While alternative 1) cannot be ruled out at present, it turns out alternative 2) is to some extent supported by current research in cosmic rays, see, e.g., Milgrom and Usov [8] , Vietri [9] , and Waxman [10] [11] , together with numerous references to the literature in these works. Thus, as is well-known, ultrahigh energy gamma rays from gamma-ray bursts impinge regularly on the Galaxy, and since gamma rays are neutral, they would not experience Cherenkov radiation loss when passing through the dark energy in the IGS. One may then be led to assume that the high energy and ultrahigh energy charged particles seen in cosmic rays are the reaction products of collisions of the incoming gamma rays with the baryonic matter of the Galaxy. At this point it should be emphasized that in the proposed model, although the speed of light is c/n in the IGS, it was assumed in I that it is c within the galaxies themselves; it was also suggested that this assumption should be tested. However, as emphasized to the author by Riess [12] , one encounters serious astrophysical problems if this were not the case, so this assumption will be maintained here. Then, with the speed of light being c in the Galaxy, if the particles were produced in such reaction processes in the Galaxy, they could reach the earth with negligible Cherenkov loss. On the other hand, since Abbasi et al. [13] [14] found in IceCube, that there was an absence of neutrinos that were to be expected to arrive in association with gamma-ray bursts, they concluded that this absence ruled out the gamma-ray explanation for the ultrahigh energy particles observed in cosmic rays.

Nevertheless, this conclusion has to be re-examined in view of the fact that although under any reasonable form of the interaction of light with the dark energy, one would expect the dispersion at the very high frequencies of the gamma rays would be such as to bring the index n down to a value very close to unity, one has to take into account that since one is dealing with an interaction for which one has no analytical knowledge, n could be so sufficiently greater than unity that neutrinos associated with the gamma rays could have arrived much earlier than the gamma rays themselves. In other words, the neutrinos could have arrived before IceCube was built! In addition, one could imagine detecting neutrinos now, and the associated gamma-ray bursts being detected some unknown number of years in the future. As a possible example, Aartsen et al. [15] detected in IceCube two PeV neutrinos that could be a prelude to a burst of gamma rays that would arrive sometime in the future. Thus, until the issue of the value of n for gamma-rays is known, and more generally, its dispersive character, one cannot rule out the possibility that gamma rays incident on the Galaxy are the source for both the ultrahigh energy and high energy charged particles seen in cosmic rays. On the other hand, this model would not rule out lower energy charged particles seen in cosmic rays to have traveled here through the IGS. A numerical estimate of the maximum kinetic energy for protons that have made the journey will be given in Section 3.

Now, if one assumes that n is indeed of electromagnetic origin, and one further assumes that the dark energy is a medium that is linear, isotropic, and non-dispersive (in the optical frequencies, as was found by the SNeIa investigators) so that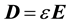, and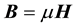, where 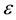and 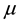are both constants. Then with 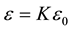and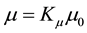, where K is the dielectric constant, and 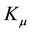is the relative permeability, since from Maxwell’s equations, 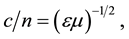one has the standard relation for the index of refraction for a linear medium given by

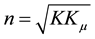. (1)

(It should be noted that, to avoid confusion, the subscript “μ” is used above rather than the customary “m”, since the latter subscript is used here to refer to matter rather than to magnetism.) Since it was found in I by a least squares analysis that n = 1.49, if one is going to employ (1) to obtain this number, it follows that one needs some dimensionless physical quantity related to the dark energy described by 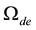(which is numerically the same as, but unlike the latter is not associated with a negative pressure), and also the totality of dark matter and baryonic matter described by.

This quantity should be greater than unity, and its square root should yield the above value for n. It was found by trial and error that setting, 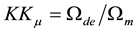, so that

, (2)

yields a reasonably close fit to the desired value. Thus in I, the fiducial values were, and, hence

, (3)

so that, which is within 8.2% of the least squares value of. The following calculation illustrates how this new value of works out for a redshift of z = 0.5, where the diminished brightness of the SNe Ia was most striking, see, e.g., the median curve in Figure 9 of Tonry et al. [16] . In Table 3 of I, the value for the additional logarithmic distance either to the SNe Ia or to the “standard ruler” of the BAO, due to the reduced speed of light, was shown to be

, (4)

and for, , it was found that. This was compared to difference between the logarithmic quantities for the accelerating universe and the Einstein-de Sitter universe that was found to be 0.080, for which the disagreement is −1.3%. This value should also be the percent disagreement, when instead of logarithmic distances are compared, apparent magnitudes are compared, since the latter satisfy. However, as was given in Table 1 in I, the percent disagreement is −2.5%. The discrepancy between the two percentages is due to round-off errors. Thus, when a sufficient number of places are utilized in both tables, one finds the percentage of disagreement for both d and is −1.3%. Upon introducing the value from (3) of into (4), one finds for z = 0.5, that d = 0.0845, and hence a disagreement with the reference value of 5.7%. Although this value is large compared to the −1.3% found above for, it should be noted that the fit to the data for the LCDM model for z = 0.5, as given in Figure 9 in Tonry et al. [16] , has an uncertainty of ~±0.04 mag or ~±10%, so the value is still within the uncertainty band. Also, it is even less in magnitude than the disagreement of 8.2% found above for the two values given for. These two results taken together suggest that the electromagnetic interpretation of n is on the right path. Nevertheless, this fairly good agreement between the two values for n could be a coincidence, and hence in the next section, as a further test, a new set of values for and are used to make a comparison between the resulting two new values for n.

3. Two New Determinations of n

As a means of attempting to determine whether the above fairly good agreement between the least squares determination of n and the square root determination is a coincidence, in this section n will be obtained in both ways for another set of values for and, based on the Planck 2015 results in Abe et al. [17] , where they give. Since both, and from the lower limit, , are so very close to used previously, it was felt desirable in the new determination to use the upper limit, , and to set, in keeping with the Einstein-de Sitter model for which, consistent with the finding in [17] that the curvature contribution is given by so that at the level of approximation used here, it is negligible. Upon using these new values, and (2), one has

. (5)

This value on n is to be compared with the least squares fit to the LCDM model that, with these new values of, and, yields

. (6)

Although these two values are within 0.7% of each other, since it is actually n − 1 that is involved in the fractional distance increase, the percentage disagreement is larger, ~2%, but it is still quite small. Also, as noted above in Section 2, the fit to the data for the LCDM model as given in [17] has an uncertainty of ±10% at z = 0.5. Thus n = 1.46 is well within the uncertainty band. Nevertheless, it is interesting to compare both values with the LCDM model, as is done below in Table 1, which is the analog of Table 3 in I. As discussed there, is proportional to the distance in the accelerating model to an object at redshift z, while is that for the Einstein-de Sitter universe. For one has

, (7)

and, for the above values of and, it is given by

. (8)

This expression, as noted in I, has to be integrated numerically. For the Einstein-de Sitter universe, with, , one has the same value for as in I

. (9)

Also, as in I, one has that.

The comparison is given in Table 1, for the two different values of n, and it is clear that the fit to the accelerating model for n = 1.46 is nearly as good as that from the least squares value, n = 1.47, and indeed is somewhat better for the higher values of z. Thus, in view of the relatively small disagreement for the fit between the two values, it is difficult to escape the conclusion that is a reasonable assumption to make, and

that it is probable that the interaction between light and the dark energy is of an electromagnetic nature, even though at this stage one cannot give more details, such as to whether it is only the dielectric constant K that is involved, or whether it is only the relative permeability that is involved, or whether both are involved. Since, , where is the mass density of the dark energy, and, and , it follows from (2) that n is also given by

. (10)

As one goes to sufficiently higher redshifts, as discussed in I, one eventually reaches a value of z for which the thermodynamic phase change that according to the model transformed the dark matter into dark energy is no longer present, and as a consequence, the dark energy that resides in the IGS has been transformed back into dark matter. Under these circumstances, n = 1, and hence it follows that for sufficiently high redshifts. This is in contrast with the ratio which is given by

, (11)

where, , from energy conservation, and. The ratio in (11) satisfies for, in contrast with the above behavior for. Thus, although at the present epoch, they differ in the present model, because does not have a negative pressure associated with it, nor is it a constant, as is the case for, since one has that, the same behavior as for the dark matter density for low z, i.e., for the present preliminary model, for, so that (10) is a constant. The analytical form of the variable behavior of the ratio is left open, but n is surely not a constant for the range of redshifts, where the larger redshift is that for which a Type Ia supernova was found that exhibited a brightness that would be the case if the universe were not accelerating at that redshift, as discussed in Riess et al. [18] . For redshifts sufficiently greater than this latter value, one has again a constant value for n, but in this case, n = 1, so that the speed of light is c throughout the universe in these earlier stages of expansion. Also since ρ_m includes baryonic matter, the resulting density of dark matter in the IGS should be greater than that associated with the galaxies in order that.

Finally, as noted in Section 2, due to Cherenkov radiation loss, charged particles traveling through the IGS will be slowed down to speeds, and hence they would have a maximum kinetic energy given by, where. For protons, with n = 1.46, this expression leads to a kinetic energy of ~350 MeV. If a significant indication of a large number of protons near this energy range were to be found in the low energy portion of the cosmic ray spectrum, presumably arriving in bursts associated with the gamma-ray bursts, it would provide an interesting test of the theory, and a direct way to measure n. Although, depending on the amount of dispersion, it is possible the gamma rays could arrive well before the protons, while on the other hand, visible light accompanying such events should arrive nearly simultaneously with the ~350 MeV protons, with the latter arriving first, since before they were slowed down by the Cherenkov radiation, they would have been traveling faster than c/n. Also, to be sure, the source need not be a gamma-ray burster, it could be any explosive event in which high energy protons were produced, along with visible light, and the protons were subsequently degraded to the Cherenkov limit as they traveled through the IGS. Also heavier nuclei, with appropriate higher kinetic energies, could accompany the protons. As a supplement to this possible low energy cosmic ray test of the model, an astronomical test is described in the next section.

4. Divergent Lensing Effect of Galaxies

As was pointed out near the end of Section 3 in I, light traveling through the galactic halos would transition from traveling at a lower speed in the IGS to higher speeds in the halos, and would finally achieve speed c in the bulk of the galaxies, and hence galaxies would act as diverging lenses. In Figure 1, this effect is shown for a foreground galaxy F, through which an astronomer at E would see, sighting along a suitable ray in the absence of obstructing stars, and/or dust, the image G' of a distant galaxy G. For simplicity, it is assumed that the galactic halo is perfectly spherical, and hence the plane projection is perfectly circular, with center at O. Also, the halo has been shrunk to a sharp discontinuity, so that within the circle, i.e., within the galaxy, n = 1, whereas, outside the circle, i.e., in the IGS, n is greater than unity. Also, again for simplicity, in Table 2 below, an average value of n = 1.23 is used, and gravitational lensing is ignored, which would obviously make the straight line rays shown in Figure 1 curved, and shift the positions of G and G' from those depicted there. Thus the straight line GE depicts the direct ray from the target galaxy G to the observer at E ignoring gravitational lensing. The line GR that meets F at R represents another ray from G that makes an angle θ with respect to the direct ray GE. The radius OR is the normal to the idealized surface of the foreground galaxy F; it is extended to meet the ray GE at R'. The angle of incidence between GR and RR' is. The incident ray GR is bent away from the normal upon entering F, and travels through F to another edge, meeting the surface at S. The angle between OR and RS is the angle of refraction, and according to Snell’s law one has., and hence. The refracted ray RS makes the same angle with the radius and normal OS as it does with OR. The normal OS is extended to meet GE at S', and the exiting ray SE makes the same angle with the normal SS' as the incident ray GR with RR'. The ray SE makes an angle θ' with respect to the ray GE. To determine the relation between θ' and θ

that depends upon n and, one observes that the angle between OR and OS, labeled, satisfies, in radians,. The angle between OR' and R'E is, and the angle between OS' and S'G is, hence one also has that. Upon the elimination of from these two relations, it follows that, and hence from Snell’s law, one has

. (12)

In Table 2, values for θ' are given in degrees for various values of θ and and for n = 1.23, the average value of the index. Small angles have been chosen so that the sighting line EG' is as close to the edge of the galaxy as possible, and so that there will be fewer stars to obstruct the sighting of the image G'. Also, it should be noted that the rays entering the Galaxy will undergo refraction, and again, for simplicity, this too has not been taken into account in (12), nor in Figure 1. Also ignored is the expansion of the universe.

The main difficulty in making such observations would be in obtaining target galaxies located relative to foreground galaxies at angles such that the image galaxy does not lie along a line of sight that passes through the central part of the foreground galaxy, thereby making the image unobservable. Other difficulties include: the fact that the shape of the halo could depart significantly from the assumed spherical shape; the recognition that one indeed has the divergent lens image of the target galaxy, and not some similar-looking galaxy; the possibility that a galaxy somewhat behind the foreground galaxy that is being gravitationally lensed has its image taken to be the target galaxy, and the galaxy that was gravitationally lensed is taken to be the divergently lensed image; finally, there may be cases where it has been assumed that one has an example of gravitational lensing, whereas instead, the lensed galaxy is in fact the image galaxy of a galaxy that has been divergently lensed.

5. A Redetermination of the Hubble Constant Based on the Model

One of the major objections to the present model, which takes as its trial basis the Einstein-de Sitter universe, is that it gives rise to an age of the universe that is smaller than the maximum age of the white dwarfs in the globular clusters in the Galaxy. For reviews, see, e.g., Krauss and Chaboyer [19] , Soderblom [20] , and Weintraub [21] . This conflict comes about as follows: the Einstein-de Sitter universe expands as, where K is a constant that is proportional to the one-third power of the mass of the universe, defined by. The time-dependent Hubble parameter defined by, , obeys the relation, and hence the reciprocal of its value at the present epoch, , the age of the universe, satisfies

, (13)

where is the Hubble constant, and is the so-called Hubble time, and is presently given as ~14.4 ´ 10⁹ yr, based on [17] , so that, whereas the ages of the white dwarfs in the oldest globular clusters are ~13 ´ 10⁹ yr, a significant disagreement. In contrast, for the accelerating universe, since it is now expanding faster than the above, after integration of the Einstein field equations with a cosmological term, one obtains a longer age of the universe of ~13.8 ´ 10⁹ yr [17] , so that the LCDM accelerating universe does not have a problem with the ages of the white dwarfs, as does the Einstein-de Sitter universe.

A resolution of this conflict for the presently proposed model has been found that is based on a re-examina- tion of the methodology used in obtaining a value for the Hubble constant. Thus, whereas the determination of the ages of the white dwarfs rely solely on measurements made within the Galaxy, the determination of the Hubble constant relies on measurements that make use of light coming from distant galaxies, and hence light coming from outside the Galaxy. Consequently, such measurements necessarily are based on light that has gone through the IGS where, unlike the situation within the Galaxy, in which the speed of light is c, the speed of light is c/n, and as will be shown next, this modifies the value of the Hubble constant, as presently determined, to yield an age for the Einstein-de Sitter universe larger than the ages of the white dwarfs, thereby eliminating the above conflict.

Now the way the Hubble relation, , is determined, is from the non-relativistic Doppler shift, , where is the observed wavelength, is the wavelength in the rest frame of the distant galaxy, v is the Hubble flow velocity of a galaxy (i.e., velocity corrected for peculiar velocity), and D is the distance to the galaxy. The redshift is defined as, where, and hence, , so that one has for the Hubble relation in terms of z

, (14)

and hence. The cosmological distance ladder (see e.g., Rowan-Robinson [22] , Freedman and Madore [23] , and Riess et al. [24] ) is used to obtain D, while spectroscopic measurements are used to obtain z. However, neither the determination of D, nor that of z, involves a time, and consequently, since the dimension of H₀ is [T]⁻¹, the way one obtains a time is from the speed of light. Since in the present model, light traveling through the IGS does not travel with speed c, but with speed c/n, the above Doppler expression should be replaced by, so that, and hence the Hubble relation becomes

, (15)

where is the corrected value of the Hubble constant, and is related to its present value H₀ by

(16)

The corresponding age of the Einstein-de Sitter universe, instead of (13), now becomes

, (17)

which is in very good agreement with the above age of the universe obtained by the accelerating model, and hence the conflict of the Einstein-de Sitter model with the maximum age of the white dwarfs is eliminated. Interestingly, the white dwarfs’ estimated maximum age can be used to set a lower bound on n using (17). Clearly, one must have that the age of the universe is greater than ~13 ´ 10⁹ yr, and hence n > ~1.35, which is obviously well satisfied. It should be pointed out that a value close to the Planck value [17] was obtained earlier by Bennett et al. [25] , i.e., 69.6 ± 0.7 km・s⁻¹・Mpc⁻¹, hence, rounding off to 70 km・s⁻¹・Mpc⁻¹, one obtains 13.6 × 10⁹ yr, which is still sufficient to eliminate the conflict with the maximum age of the white dwarfs.

One obtains the same result as (16) by using, instead of the Doppler expression, the modified FLRW line element, , with for flat space. Upon setting ds² = 0, expanding a(t) as (ignoring higher derivatives), solving for r, and ignoring non-linearities, as shown in texts on the subject, one finds Since the proper distance D, locally, is given by, one has finally, , in agreement with (15). However, it should be emphasized that one cannot use the above line element for in mechanical problems, because it would imply that c/n is the limiting velocity for massive particles, which is not the case. See, e.g., the interesting discussion in Cox [7] . One should therefore imagine for these cases, as well as for light of sufficiently short wavelength, that n = 1, and hence the classical Minkowski line element holds locally, and that of Einstein-de Sitter holds globally. There is an interesting analogy here with quantum mechanics, since when the de Broglie wavelength tends to zero, the particle behaves classically; however, a further discussion of this analogy is beyond the scope of this work.

Since, and hence depends on the Hubble constant, it is desirable to show that, nevertheless, n does not depend on the Hubble constant, since n is a local property of the dark energy over the redshift range that is being considered in which n is assumed to be a constant. Thus, in determining n by means of the square root relation (2), ρ_c cancels, and (2) reduces to (10), which only involves ρ_de/ρ_m, and hence n determined in this way is independent of the Hubble constant. Likewise, in determining n by the least squares method, that corrects with the aid of the factor, , the distance given by the Einstein-de Sitter model to agree with that given by the ΛCDM model, a similar cancellation occurs. This is because the ratio of X_Λ given in (7) to X_m given in (8) is involved, in which, again, the density ρ_c cancels. To show this, one has that

, where f_Λ denotes the integral in (7), and since the ratio Ω_Λ/Ω_m is independent of

ρ_c, only the factor contains it. Likewise for X_m, the integral f_m in (8) is independent of ρ_c, and although

the factor in this case is unity, it is actually in which ρ_m has the same value as ρ_c. Consequently, upon taking the ratio X_Λ/X_m, once again ρ_c cancels, and hence since, each value of (n − 1) determined from this relation, is independent of ρ_c, for the range of z used to obtain the least squares value, and since the mean of the sum of the ten values of n − 1 obtained from the above relation yields the least squares value of n, it too is independent of ρ_c, and hence it is independent of the Hubble constant.

Finally, although the proposed new value of the Hubble constant has been written as, this is only a temporary expedient to avoid confusion with the current value denoted by H₀, that is based on the speed of light in the IGS as being c. If the proposed reduction of the speed of light through the IGS proves correct, the asterisk superscript could be eliminated, and the present value of would become the new value of H₀.

6. Concluding Remarks

The present work revises the view expressed in I that the interaction of light with the dark energy was not of an electromagnetic nature. As was shown above, the assumption of an electromagnetic interaction leads to a value of n in good agreement with that obtained from a least squares fit to the accelerating model for the fiducial values of density parameters used in I, and to an excellent agreement with that model when more recent values are used. Further, as was pointed out, the assumption that the interaction is electromagnetic means that one has to assume that the high energy charged particles found in cosmic rays could not have reached the Galaxy through the IGS, because of the energy they would have lost due to Cherenkov radiation. Instead, the model supports the widely discussed view that the high energy charged particles seen in cosmic rays are produced through collisions with the baryonic matter in the Galaxy by incoming high energy gamma rays that presumably originate from gamma-ray bursters, or collapsars, and/or some other high energy gamma-ray sources. The absence of predicted accompanying neutrinos from the gamma ray bursts [13] [14] as discussed in Section 2, could be due to the fact that the photons travel less than the vacuum speed of light, so that the neutrinos arrived at IceCube much earlier than the gamma rays, possibly well before IceCube was built. Also, there could be high-energy neutrinos detected without any evidence of an accompanying gamma-ray burst [15] , since if the gamma-rays travelled less than the vacuum speed of light, they would arrive sometime in the future. For completeness, it should be noted that because the neutrinos have such small rest masses and such high energy, their speed is so close to the vacuum speed of light that the difference is negligible for these considerations. Also, as was noted that charged particles could travel through the IGS for cosmic distances provided, they did not exceed the limit imposed by Cherenkov losses. For protons this turned out to be a limiting kinetic energy of ~350 MeV, and therefore there could be surges in protons and their collision products at or just below this energy in the cosmic ray spectrum.

Turning next to astronomical tests of the proposed model: as discussed in Section 4, according to the model, there should be divergent lensing of more distant galaxies by foreground galaxies. If one fails to find any examples of divergent lensing, this would rule out this proposed alternative to the accelerating universe. Also, as discussed in Section 5, the ages of the oldest white dwarfs in the Galaxy can be accommodated by the present model, because it predicts a smaller value for the Hubble constant than its present value.

Significant theoretical challenges remain. One has to show that despite the extremely low density of the dark energy, it is possible for it to give rise to such a large index of refraction, and to determine through dispersion relations, its frequency dependence,. A further challenge is to derive an expression for n(z), the behavior of the index of refraction as a function of redshift, which in the proposed model has been taken to be a constant for the range from z = 0.1 to z = 1.0, both in the Table 1 here, and in the three tables in I. Finally, contributions to Ω_tot from the Cosmic Microwave Background Radiation, neutrinos, and possible spatial curvature have been omitted; these too will have to be included in future more detailed models.

Acknowledgements

I am thankful to Professor Adam Riess for a helpful critical comment concerning the previous work. I would also like to thank Professor Thomas Murphy for another helpful critical comment as well.

Cite this paper

Frank R.Tangherlini, (2015) A Possible Alternative to the Accelerating Universe II. Journal of Modern Physics,06,1360-1370. doi: 10.4236/jmp.2015.69141

References