Received 6 July 2015; accepted 26 October 2015; published 29 October 2015

ABSTRACT

Theoretical investigation of generation-recombination processes in silicon, which has a lifetime of charge carriers 10⁻³ s and capture cross sections of 10⁻¹⁶ sm². For the study uses a method of phase portraits, which are widely used in the theory of vibrations. It is shown that the form of phase portraits strongly depends on the frequency of exposure to the external variable deformation.

Keywords:

Phase Portraits, The Generation of Charge Carriers, The Recombination of Charge Carriers

1. Introduction

For the analysis of all possible movements (natural vibrations) is “phase plane”. In mechanics, statistical physics and introduction of the concept of “phase space”, in the one case, it degenerates into a plane space. Analysis of the oscillating system using phase portraits has the advantage of clarity, and is a powerful tool for the study of oscillatory processes [1] .

Variable external influence on the semiconductor structure may cause the alternation of the generation and recombination processes. This process of generation and recombination in nature is similar to the oscillatory process. Study of generation-recombination processes using phase portraits can give a fairly complete picture of the processes in semiconductors. In [2] , they were obtained according to the concentration and resistance to deformation of the semiconductor film. It was shown that these relationships gave graphs pretty clear ideas ongoing processes in semiconductor films, namely the distortion of the closed curves talking about the emergence of new recombination centers. The emergence of new recombination centers is due to structural changes in semiconductor films, which are associated with films fatigue due to long exposure deformation. Thus, the above dependency graphs are allowed to diagnose conditions of semiconductor materials. However, in [2] , the phase portraits of the processes of the semiconductor film were not considered.

In this paper, by using the phase portraits the effect of variable frequency strain on the semiconductor film is investigated.

2. The Impact of the Variable Frequency Strain Concentration of Nonequilibrium Charge Carriers

Under the effect of the deformation occurs changes the band structure leads to changes in the concentration of charge carriers, and a redistribution of charge carriers between energy valleys [3] . These changes in turn lead to a change in resistance of the sample [4] . If the external deformation will be variable, then the change in resistance of the sample at the time occurs with some lag from the applied mechanical impact. Consider the response of the excess electron concentration ne a variable deformation. Deformation can induce the generation of electrons at a rate ge moreover, excessive electrons may come from another area of the sample [5] [6] . The concentration can be determined by the equation of continuity

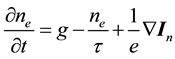, (1)

where 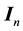the current density of electrons, t-the electron lifetime. In a homogeneous sample is given by the equation of continuity

. (2)

The solution of Equation (2) in the case where the deformation of e is a random function of time, is given by [6]

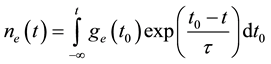. (3)

Equation (3) can be used to determine the magnitude of the concentration of non-equilibrium reacts to changing deformation. Assume that the deformation varies sinusoidally

. (4)

Then, the band gap varies according to the same law

. (5)

here -the deformation potential [5] [7] . The rate of heat generation has an exponential dependence of the band gap and lattice temperature [4] [8] . In this case, the general thermodynamic considerations, the rate of generation of non-equilibrium carriers can be represented as follows

. (6)

Then, from the expression (3) and (6) we have

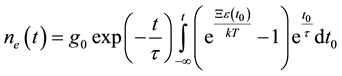. (7)

By specifying an explicit form of time-dependent strain ε(t) can be obtained from the time dependence of the concentration n_e(t) from time to time. Equation (7) in a fairly wide range of deformation function e(t₀) allows to describe the change of the carrier density.

To demonstrate the method of preparation according n_e-ε, we consider a weak deformation, i.e.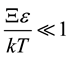. Then,

the expression (7) can be written as

. (8)

Let the sample is applied a sinusoidal deformation half-period 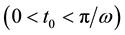and other times there is no deformation. Then from (8) we have

. (9)

After the end of the deformation in the formula (8), the upper limit of the integral is to be p/w

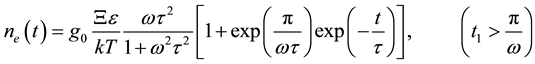. (10)

Changing the frequency of external influence is making a tangible contribution to the concentration vs. time. Since the change in the external effects of low frequencies in the non-equilibrium charge carrier concentration will increase and decrease gradually. That is, there will be some period of time between generation and recombination of charge carriers from zone to zone. And when the frequency reaches the maximum values decrease and increase of charge carriers becomes imperceptible. In other words, the generation-recombination processes do not have time to react to changes in the band spectrum of the semiconductor and the concentration of charge carriers takes a steady average.

Figure 1 and Figure 2 present illustrative examples of the concentration of charge carriers of the time under the influence of deformation of the variable frequency. The growth rate was 3 Hz frequency in every 0.01 second. When plotting used expression (9).

Consider the case where a variable deformation influences with increasing frequency in the semiconductor structure. Assume that the initial generation and charge carrier lifetime is respectively g₀ = 10¹⁸ and τ = 10⁻³ [9] . With the growth rate of deformation of the variable ω₀ = 3 Hz to ω = 210 Hz (see Figure 1(a)) a decrease in the concentration ranges. For example, if the frequency ω₀ = 3 Hz change in the concentration range was n ≈ 0 - 2 × 10¹⁵ cm⁻³, then the frequency ω₀ = 210 Hz range was the change in concentration n ≈ (5 × 10¹²) - (1.9 × 10¹⁵) cm⁻³. When the frequency of the alternating deformation reaches ω = 900 Hz (see Figure 1(b)) changes in the concentration range of ≈(3 × 10¹³) - (7.5 × 10¹⁴) cm⁻³.

With increasing frequency of the alternating deformation range of the concentration of charge carriers takes some average. As can be seen in Figure 2 when a variable frequency is 30 kHz deformation range of the charge carrier concentration varies between 10¹⁵ cm⁻³ to increase the frequency up to 54 kHz. This suggests that the concentration of nonequilibrium charge carriers acquired its steady average.

Apparently by prolonged exposure of the periodic pattern deformation in semiconductor recombination centers may occur in crystal lattices. As a result, the development of the processes of generation and recombination can take a different turn, and accordingly the concentration of charge carriers may have a deviation from the established mean.

The case where the frequency itself changes periodically variable deformation, ranges from 0 to 20 kHz is shown in Figure 3. Analysis of Figure 3 shows that as the frequency variable deformation reaches a maximum value, set the average concentration becomes a value within 10 × 15 cm⁻³. When the frequency of the variable deformation reaches a minimum value, a range of changes in the concentration ranges from 0 - 2 × 10¹⁵ cm⁻³. This is repeated for two seconds to 8 times.

3. Phase Portraits of the Concentration of Charge Carriers from the Rate of Change of the Charge Carriers Concentration

To obtain the phase portrait is usually considered the dependence of some parameter x of its derivative. Since

the deformation by changing the energy spectrum affects the generation-recombination processes, to obtain the phase portrait of such processes must be obtained from the dependence of the concentration n of its derivative

, or the dependence of resistance on its derivative.

Consider the case of silicon, which has a lifetime of charge carriers 10⁻³ seconds capture cross 10⁻¹⁶ cm² [9] .

The phase portrait is the largest area when the frequency of the alternating deformation is 1000 Hz (see Figure 4(a)). That is, the phase portrait is the largest area when, here the generation and recombination of charge carriers takes place gradually. With the change in frequency of the alternating deformation changes the shape of the phase portraits (see Figures 4(b)-(f)). In the case where the frequency of the alternating deformation increases, and the product of frequency and time of life become, the shape of the phase portrait is committed to the horizontal segment (see Figure 4(f)), that is, generation and recombination of charge carriers is almost not felt. In the opposite case, when the frequency of the alternating deformation decreases, and the product of frequency and time of life become, the shape of the phase portrait is committed to the vertical segment (see Figure 4(f)), is the generation and recombination of charge carriers is shown sharply.

Three-dimensional phase portrait is shown in Figure 5. This graph is obtained for the case when the charge carrier lifetime 10⁻² s, and capture cross sections of 10⁻¹⁶ cm².

4. Conclusions

Thus, the shape of the phase portraits allows us to determine how to respond to the frequency change of the semi- conductor strain. Namely, with increasing frequency variable strain rate and the product carrier lifetime become, the shape of the phase portrait is committed to the horizontal segment. If the variable frequency distortion and carrier lifetime of the product become, the shape of the phase portrait is committed to the vertical segment. The phase portrait is the largest area when.

This work was supported by government grants of Uzbekistan F2-OT-O-15494 “Improving the efficiency of the radiators, solar cells and other optoelectronic devices based on quantum dot research and hetero nanostructure exciton and bipolaron transport phenomena”, F2-FA-0-97004 “Dynamics of solitons in ultracold quantum gases, and optical systems and synergistic processes in multicomponent semiconductors” and F2-21 “Mathematical modelling of the determination of the density of surface states at the semiconductor-insulator”.

Cite this paper

GafurGulyamov,A. G.Gulyamov,A. Q.Ergashev,B. T.Abdulazizov, (2015) The Use of Phase Portraits for the Study of the Generation-Recombination Processes in Semiconductor. Journal of Modern Physics,06,1921-1926. doi: 10.4236/jmp.2015.613197

References