Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52820,7 pages
10.4236/jmp.2014.518213
Wave-Particle Duality in Einstein-de Broglie Programs
Claude Elbaz
Academie Europeenne Interdisciplinaire de Science (A.E.I.S.), Paris, France
Email: claude.elbaz@science-inter.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 October 2014; revised 18 November 2014; accepted 14 December 2014
ABSTRACT
The standard model of particle physics forms a consistent system for universe description. After following quantum mechanics, it derives particles from relativistic quantum fields. Since it does not include gravitation, it describes only one aspect of the universe. In extension of general relativity, Einstein had proposed a symmetrical and complementary approach of physics. In his program, he privileged a relativist field based on representations for physical phenomena, before a precise mathematical description. It allows completing and unifying the universe description, like both eyes for relief vision, and both ears for stereophonic audition. We propose to show it with many simple examples.
Keywords:
Standard Model, Quantum Theory, Special Relativity, de Broglie Relation, Planck-Einstein Relation, Gravitation, Planck Parameters

1. Introduction
The problems of wave-particle and matter-light dualities had, along centuries, divided philosophers at first, before physicists. The basic models are physically and mathematically opposed and complementary, since the waves are extended through space while the particles are concentrated. This justifies why physicists admitted either one model, or the other, as more fundamental for the basic structure constitution of the universe.
In 1905, from the photoelectric effect, Einstein introduced the first quantum particle with the energy light quanta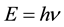 , nowadays called photon [1] . Symmetrically, in 1924, Louis de Broglie established that the electron, and more generally matter, with energy
, nowadays called photon [1] . Symmetrically, in 1924, Louis de Broglie established that the electron, and more generally matter, with energy , behaved also as wave [2] . Each of them was awarded a Nobel Prize for his discovery.
, behaved also as wave [2] . Each of them was awarded a Nobel Prize for his discovery.
Henceforth, for the physicists, the whole universe is described by the standard model. It is constituted by matter interacting through four different kinds of forces. It must be considered as finally formed by quantum particles behaving either as waves or as particles. It has been validated in 2012 by the BEH, or Higgs, boson detection, which represents its crowning.
The standard model forms a consistent system for universe description. It extends quantum mechanics, which had privileged mathematical formalism to describe the behavior of a single particle. The wave character, exhibited by experience, is described by a point-like probability density, with a mathematical formalism, in which Heisenberg’s relations act as a limiting frame.
However, the standard model differs from quantum mechanics, and goes beyond it, since it leans on relativist quantum fields. They no longer restrict to a single particle, but apply to many identical particles, each one being created or annihilated inside the corresponding field. The two basic categories of quantum particles, the bosons and the fermions, differ from one another by their statistical properties, which are then in relation with sets of particles: Bose-Einstein statistic laws for the first one and Fermi-Dirac for the second. A single particle appears only as a particular manifestation of a more fundamental continuous field, expressed mathematically by partial derivative equations.
The standard model describes only a partial aspect of the universe. For example, it does not include gravitation. It is then posterior to Planck era.
By comparison, gravitation is well described by general relativity, which is a classical theory, based on a continuous field. It has been largely confirmed by numerous experiments and by its theoretical consequences and practical applications. The graviton, as the quantum particle mediating gravitation interaction, has not yet been detected and validated. Consequently, until having proof to the contrary, gravitation remains described by general relativity, which is a classical theory.
One of the most present resisting problems in physics lies in the reconciliation of gravitation with electromagnetism. The problems of wave-particle and matter-light dualities are then far for being entirely solved.
In extension of general relativity and of his different discoveries, including in quantum physics such as the stimulated emission, Einstein had proposed a consistent approach for physics, symmetrical to the standard model [3] . He privileged the continuous field, leaning on physical representations of phenomena, before their more precise mathematical description.
Einstein’s program allows us to complete the universe vision, like both eyes give us access to tridimensional vision, or both ears to stereophonic audition.
In this article we propose to show it through many simple examples.
2. History
2.1. Particles
Since antiquity, Democritus had considered that universe is composed of atoms and vacuum. Atoms represent the ultimate stage of matter division. They are physically indivisible and indestructible…. between atoms lies empty space. Two millenniums later, for Newton: “It seems probable to me that God in the beginning formed matter in solid, massy, impenetrable, moveable particles… even so very hard, as never to wear or break in pieces; no ordinary power being able to divide what God himself made one in the first Creation… particles are separated by empty space.” At present time, with the standard model, we admit that all material particles of universe were created at nucleosynthesis era, 13.8 billion years ago, less than 3 minutes after universe.
To summarize: the concept of material particle is characterized by a double discontinuity, in space and in time. In space, by delimiting an inner “full” part, and an outer “empty” part. In time, by delimiting a prior time before its creation, and a posterior time after, during which it is present.
2.2. Fields and Waves
On another hand, since antiquity also, Aristotle considered that space was not empty and that “nature abhors vacuum”. Two millenniums later Descartes eliminated the void in nature. For him, “matter is a continuous fluid, homogeneous, characterized by its extent, and which fills up whole universe”. It allows the transmission of light as a pressure. After him, Huygens, contemporary of Newton, introduced his wave theory of light, deriving the laws of optics. However, his model has arisen only in the 19th century, after Fresnel and Maxwell.
When the field was introduced in physics, it began to designate the instantaneous force exerted, in each point of space, between matter particles or electric charges, through space vacuum. The speed of light detection, and its propagation step by step in space as waves, led to assign a physical nature to space: the electromagnetic aether.
In 1905, the special theory of relativity allowed Einstein to suppress electromagnetic aether need, in order to fill the space vacuum; however the general theory of relativity led him to reconsider that space ought to have a physical fundamental role. “Empty space is neither homogeneous, nor isotropic… these facts had definitely dismissed the conception that space was physically empty. From this, the aether notion has acquired a new precise content, which of course differs notably from the aether of mechanical wave theory of light. The aether of general relativity is a medium deprived of all mechanical and kinematical properties, but determines mechanical and electromagnetic phenomena [4] .” Actually, the content of empty space is no longer characterized by aether, but rather by space-time. In standard model, “the empty space of a quantum field theory behaves as a complex medium in which quantum fields are submitted to fluctuations physical effects are observable”.
To summarize: by difference with the field concept, which expresses an interaction between particles, the wave concept renders essential the role of the medium and the propagation velocity: a wave continues to propagate in space, even though its localized origin had disappeared, like the cosmological background radiation, detected 13.8 billion years after its emission.
2.3. Wave-Particle and Matter-Light Duality
With Einstein, classical relativist physics includes gravitation but not quantification. With the standard model, relativist quantum physics includes quantification but not gravitation. In both cases, the concepts of particles, discontinue and localized in space and time, and waves, continue and extended in space and time, subsist. Thus, the standard model in one hand, and general relativity in other hand, describe only one aspect of universe. Each one forms a consistent system, which has been validated by experiment with great precision.
The standard model extends quantum mechanics, which privileged particle by leaning upon mathematical formalism at first. The Einstein’s program proposes a symmetrical approach. He privileged a continuous field, by leaning on physical representations of phenomena, before their more precise mathematical description.
Both approaches are complementary. They allow access to a unitary grasp of universe, somewhat like both eyes to relief vision, or both ears to stereophonic hearing.
The standard model in one hand, and the Einstein’s program in other hand, must be considered as two consistent systems to perceive physical phenomena, somewhat like those recorded by two relativist observers, one setting on a moving train and the other on the platform at rest. Each one notices that his environment is at rest for him; and must serve for recording references, while the other is moving, and then affected by the speed. A same observer cannot overlook a simultaneous general view of phenomena by setting on the platform with one foot and in the moving train with the other.
3. The Standard Model of Particles
In the synthetic standard model table for the basic components of universe that have been validated by experiment, the material and interaction particles are classified in two sets, according to their relativist quantum properties: fermions and bosons (Figure 1).
We remark that gravitation does not figure. This is justified owing to the fact that, at particles level, quantum effects are preponderant, while gravitation is negligible. In addition, despite many experimental investigations, the graviton, as mediating quantum particle, has not been detected and validated still. Thus far, the synthetic table contents confirm that the standard model describes only one aspect of universe.
When we take account of particles classical relativist properties, we can adopt another method of grouping, according as they have a rest mass or not. The distinction is exclusive since particles without mass, like photons and gluons for interactions, have motion velocity always equal to light speed: it can never be different. On the contrary, particles with mass, like fermions for matter, have a motion velocity always inferior to light speed: never it can be equal.
4. Einstein’s and de Broglie’s Programs
It is known that Einstein won his Nobel Prize in 1921, not for special followed by general relativity theories, but for introducing, in 1905, the first quantum particle from energy light quanta, nowadays called photon. In exten-
Figure 1. Different particles of the standard model.
sion of general relativity and of his different discoveries, including in quantum physics, such as the stimulated emission, Einstein had proposed a consistent approach for physics, symmetrical to the standard model: “We have two realities: matter and field... We cannot build physics on the basis of the matter concept alone. But the division into matter and field is, after the recognition of the equivalence of mass and energy, something artificial and not clearly defined. Could we not reject the concept of matter and build a pure field physics?... We could regard matter as the regions in space where the field is extremely strong. In this way a new philosophical background could be created... Only field-energy would be left, and the particle would be merely an area of special density of field-energy. In that case one could hope to deduce the concept of the mass-point together with the equations of the motion of the particles from the field equations―the disturbing dualism would have been removed... One would be compelled to demand that the particles themselves would everywhere be describable as singularity free solutions of the completed field-equations. Only then would the general theory of general relativity be a complete theory... One could believe that it would be possible to find a new and secure foundation for all physics upon the path which had been so successfully begun by Faraday and Maxwell [3] - [5] .”
Einstein, who usually reasoned theoretically with thought experiments, recommended to lean on physical representations of phenomena, before a more precise mathematical description: “Most of the fundamental ideas of science are essentially simple, and may, as a rule, be expressed in a language comprehensible to everyone. To follow up these ideas demands the knowledge of a highly refined technique of investigation. Mathematics as a tool of reasoning is necessary if we wish to draw conclusions which may be compared with experiment. So long as we are concerned only with fundamental physical ideas, we may avoid the language of mathematics.”
In previous articles [6] - [9] , we showed how we could retrieve matter main physical properties when, consistently with Einstein’s and de Broglie’s programs, we admitted the field propagating at speed of light as its basic structure. Matter corresponds to standing waves, while its interactions correspond to progressive waves. Classical relativist equations of mechanics correspond to geometrical optics approximation, when very high frequencies are hidden, while only mean effects appear. Equations of quantum mechanics take oscillating frequencies in account. The variations of frequencies lead to Fourier relations, homogeneous to the field, leading to the Heisenberg relations, homogeneous to matter. They lead also to interactions, which are formally identical with electromagnetism, as to variational principle and energy-momentum conservation laws. The variations of speed of light lead to an interaction, which is formally identical with gravitation.
Consequently, it is possible to adopt a consistent approach of physical phenomena when, following Einstein’s program, we admit that waves propagating at the speed of light are the basic components of matter and interactions. When frequencies are infinitely high, they render oscillations inaccessible with time, since they are too rapid, and with space, since the wavelengths are too small. Physical phenomena exhibit then, theoretically and experimentally, as particles.
Such an approach permits to complete and unite a general grasp of physical universe, as we propose to show with many simple examples.
5. Validation by Experiment of Einstein’s and de Broglie’s Programs
5.1. Einstein’s Program Validation
As a general manner, new technologies evolve in accordance with the Einstein’s program when they are substituting, progressively and almost systematically, mechanical devices by electronic devices, based upon electromagnetic field in place of matter. For instance, instead of printing documents on paper, they are rather numerically recorded.
What is more specific is that, decades after the Einstein’s program was set, physicists had begun to bring it into effect, when they replaced international standards of length and time, based on matter since two centuries, by electromagnetic standards, based on the period of a continuous field propagating at the speed of light.
Nowadays the second is defined from the radiation of the cesium 133 atom. In parallel, the speed of light in vacuum is admitted as fundamental, with its value strictly fixed. This allows to measure durations with 10−18 precision. Such measures, carried out by electromagnetic frequencies reduction ratio, are the more precise in physics at the present time [10] [11] . The precision, as compared to that reached in relativist quantum fields with the Lamb shift, or in general relativity, goes beyond many magnitudes [12] - [14] .
Such an approach, using electromagnetic wave, instead of material, devices, does not concern specialized physicists only. Everybody is now progressively involved in his confrontation with physical nature. For instance, one has, at his disposal laser telemeters for measuring lengths. They are not only more precise and more rapid, but the numerical data acquisition can be coupled with different kinds of treatments: technical, economical, commercial…
As far back as 1905, when Einstein established special relativity theory, he used a light ray, and not a material rod, to measure the distance of a moving body. He anticipated the international length standard adopted in 1960 by the International Legal Metrology Organization. He has been indirectly at origin of electromagnetic standards since, in a report of the International Committee on Intellectual Cooperation he signed conjointly with M. Curie and H.A. Lorentz in 1927, he recommended the establishment of an international bureau of metrology. It was effectively created in 1955, the year of Einstein’s death. Its first work has been the elaboration and adoption of length and time standards, based on light radiation.
5.2. de Broglie’s Program Validation
The Louis de Broglie’s theoretical discovery of wave properties for moving matter, with a wavelength , was soon followed by their experimental verification and validation [6] [15] [16] . They led to matter wave optics developments based on electrons, neurons, protons, atoms and molecules, even on large molecules such as fullerene (C60) [17] - [22] . They led for instance to the construction of electron microscopes, with magnitudes 5000 times higher than light microscopes [23] , and to numerous applications in different sciences and techniques. The 10−18 precision obtained in metrology, is carried out by atomic interferometry, based upon de Broglie’s matter waves.
, was soon followed by their experimental verification and validation [6] [15] [16] . They led to matter wave optics developments based on electrons, neurons, protons, atoms and molecules, even on large molecules such as fullerene (C60) [17] - [22] . They led for instance to the construction of electron microscopes, with magnitudes 5000 times higher than light microscopes [23] , and to numerous applications in different sciences and techniques. The 10−18 precision obtained in metrology, is carried out by atomic interferometry, based upon de Broglie’s matter waves.
6. Compton Scattering
6.1. Particles Collisions
The Compton scattering is usually interpreted, in terms of particles, as an inelastic collision between an electron and a photon. The change in wavelength of light, deduced from by Compton equations, is admitted as a conclusive experimental proof that light is composed of particles, the photons, as well as matter is composed of electrons in atoms
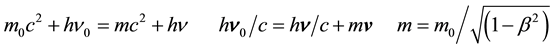 (1)
(1)
The incident photon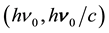 , is absorbed by an electron at rest
, is absorbed by an electron at rest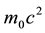 . It transfers its energy and momentum, setting the electron in motion
. It transfers its energy and momentum, setting the electron in motion , with emission of a photon
, with emission of a photon .
.
These equations are considered as successive in time. In the direct Compton scattering the left terms of the equations disappears to leave place to the right terms. In the inverse Compton effect, the opposite process occurs. In these conditions, the mathematical solution of (1) , where terms of both sides are linked, is not physically retained as sense deprived: the rest electron cannot interact with the emitted photon before its creation time.
, where terms of both sides are linked, is not physically retained as sense deprived: the rest electron cannot interact with the emitted photon before its creation time.
In particle point of view for light, physical consequences, derived from the Compton equations, are less complete than their mathematical consequences.
6.2. Wave Scattering
Since all quantum particles of matter and interactions behave indifferently as particles or as waves, we can equally interpret the Compton equations in waves terms. Already, since their origin, their solution exhibited a Compton wavelength , before Louis de Broglie associated an oscillatory frequency N0 to matter with rest mass
, before Louis de Broglie associated an oscillatory frequency N0 to matter with rest mass , such that
, such that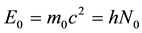 , leading to a wavelength
, leading to a wavelength  when in motion with speed v.
when in motion with speed v.
In mathematical point of view, the developments of solutions in (1),
 (1)
(1)
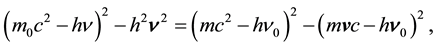 (2)
(2)
lead to reciprocal relations, where q0 and q designate the directions of the incident and emitted photons with regard to the electron speed v, and where the Planck’s constant is no longer present,


We recognize the relativist laws of light reflection from a moving mirror with speed 
The reciprocal relations (3) and (4) point out the relative character of energies and frequencies: in agreement with special relativity, we can then either consider that the left terms, or the right ones, of the Compton Equation (1) are at rest. The frequencies n0 and n characterize the same light wave, depending of measuring it either in moving or in rest system, according to the Doppler effect.
In wave point of view for light, physical consequences, derived from the Compton equations, are more complete than those derived from their particle properties.
6.3. Particle-Wave Quantum Duality
In both cases; despite the Planck’s constant presence, the Compton Equations (1) are determinist, with a well defined time boundary which separates the two successive states. The electron is either at rest or in motion. The wave light, or the photon, has either a frequency n0 or n. The supplementary Heisenberg’s relations introduce an intermediary domain, as a “fuzzy boundary which separates quantum and classical worlds” [28] . As a consequence, the equivalence between the indetermination Dx of the particle position, verifying the relation 

In these conditions, “since the photon is generally observable only when it disappears, a new type of atomic detector, able to record the trace of a single photon, without absorbing energy” [28] , has been realized by S. Haroche and his collaborators.
Such an experiment illustrates the particle-wave duality behaviour of matter and interactions quantum particles still more [29] .
7. Planck Parameters
7.1. Planck Era
From numerical values of fundamental physical constants, speed of light c, Planck’s constant h, and gravitation constant G, and their dimensional equations with respect to length L, time T, and mass M,

we derive the numerical values of the physical quantities M, L, T which define the Planck’s parameters.

(Usually one uses the reduced Planck constant h-bar = h/2л, instead of h, which divides all values by
The dimensional equations are physically independent of wave or particle interpretations. Since gravitation is not included in the standard model of particles, it is admitted that these parameters define the Planck’s epoch, which took place when the four interactions, including gravitation, were united, before matter particles creation. These parameters values then represent the standard model application limits.
7.2. Wave-Particle Planck Limits
From the Planck-Einstein-de Broglie fundamental relations for the self energy of a matter particle, 




we retrieve the numerical values of the Planck parameters (6), by calculating m, T and λc , with respect to h, c and G.
The fundamental equations of a matter particle (7) remain always valid in the universe at present time. The boundaries they define are not restricted to a very brief epoch in the earliest time following the universe emergence. They all rather continue to apply.
The relations (7) conciliate at one and the same time the particle aspect of matter, particularly through its gravitation self energy 

References
- de Broglie, L. (1955) Le dualisme des ondes et des corpuscules dans l’ceuvre de Albert Einstein. Académie des Sciences, Paris, 27.
- de Broglie, L. (1963) Recherche sur la theorie des quanta. Masson, Paris.
- Diner, S., Fargue, D., Lochak, G. and Selleri, F. (1984) The Wave-Particle Dualism (A Tribute to Louis de Broglie 90th Birthday). Reidel Corp.
- Einstein, A. and Infeld, L. (1938) The Evolution of Physics. Cambridge University Press, Cambridge, 228-232.
- Einstein, A. (1920) The Aether and Relativity Theory. Leyde University, Leyde.
- Einstein, A. (1949) Philosopher, Scientist. Cambridge University Press, London.
- Elbaz, C. (2013) Annales de la Fondation Louis de Broglie, 38, 195-217.
- Elbaz, C. (2010) Asymptotic Analysis, 68, 77-88.
- Elbaz, C. (2012) Discrete and Continuous Dynamical Systems, A.I.M.S, Series B, 17, 835-849.
- Dimarcq, N. (2013) La mesure du temps. http://www.planetastronomy.com/special/2014-special/05nov/Dimarcq-IAP.htm
- Salomon, C. (2014) La mesure du temps et les tests de la relativite, ENS, LKB.
- Boudet, R. (1989) Annales de la Fondation Louis de Broglie, 14, 119-146.
- Boudet, R. (2009) Relativistic Transitions in the Hydrogenic Atoms. Springer-Verlag, Berlin.
- Boudet, R. (2011) Quantum Mechanics in the Geometry of Space-Time. Springer Briefs in Physics, 7-11.
- Davisson, C.J. and Germer, L.H. (1927) Nature, 119, 558-560. http://dx.doi.org/10.1038/119558a0
- Logiurato, F. and Smerzi, A. (2012) Journal of Modern Physics, 3, 1802-1812. http://dx.doi.org/10.4236/jmp.2012.311225
- Logiurato, F., Gratton, L. and Oss, S. (2008) The Physics Teacher, 46, 109. http://dx.doi.org/10.1119/1.2834534
- Cronin, A., Schmiedmayer, J. and Pritchard, D.E. (2009) Reviews of Modern Physics, 81, 1051. http://dx.doi.org/10.1103/RevModPhys.81.1051
- Laloë, F. (2001) American Journal of Physics, 69, 655. http://dx.doi.org/10.1119/1.1356698
- Jorgensen, T.P. (1998) International Journal of Theoretical Physics, 37, 2763-2766. http://dx.doi.org/10.1023/A:1026689008592
- Hobson, A. (2013) American Journal of Physics, 81, 211. http://dx.doi.org/10.1119/1.4789885
- Berninger, M., Stefanov, A., Deachapunya, S. and Arndt, M. (2007) Physical Review A, 76, Article ID: 013607. http://dx.doi.org/10.1103/PhysRevA.76.013607
- O’keefe, M. (2011) World Record Resolution at 0.78 Angstr. MCEM, Bekeley Lab.
- Jennison, R.C. and Drinkwater, A.J. (1977) Journal of Physics A, 10, 167. http://dx.doi.org/10.1088/0305-4470/10/2/005
- Jennison, R.C. (1980) Journal of Physics A, 13, 2247. http://dx.doi.org/10.1088/0305-4470/13/6/043
- MacKinnon, E. (1975) American Journal of Physics, 44, 1047. http://dx.doi.org/10.1119/1.10583
- Elbaz, C. (1987) Journal of Physics A: Mathematical and General, 20, L279-L282.
- Haroche, S. (2007) Vie et mort d’un photon: Une autre manière de voir. Lettre du collège de France, No. 20, june 2007.
- Haroche, S. (2013) La dualité onde-particule. Rome.



