Journal of Modern Physics
Vol.5 No.6(2014), Article ID:45407,13 pages DOI:10.4236/jmp.2014.56060
The Structure of Icosahedral Quasicrystals and Seven Blunders in Quasicrystallography
Antony J. Bourdillon
UHRL, San Jose, USA
Email: bourdillona@sbcglobal.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 21 December 2013; revised 18 January 2014; accepted 11 February 2014
ABSTRACT
This structural study of quasicrystals is based on extremely dense icosahedral unit cells that are systematically and consistently measured for the first time. The structure and pattern indexation are 3-dimensional. A formula is given for scattering from atoms in hierarchic arrangement and geometric series. The Quasi-Bragg law is a new law in physics, with possible applications beyond crystallography. The structure is compared with previous, unsuccessful, and contradictory, attempts at analysis.
Keywords:Icosahedral Quasicrystals, Logarithmic Periodicity, Quasi-Bragg Law, Metric, Geometric Series, Icosahedral Unit Cell, Blunders

1. Introduction
The structural solution for icosahedral quasicrystals has been described in several journal publications [1] [2] , monographs [3] -[7] and warmly received at several conferences e.g. [8] . For clarity and simplicity, the solution has been summarized in introductory video records [9] . The theory has been thoroughly debated1, and all negative reviews are provided and refuted in the work cited. To fix ideas, the many-sided solution is summarized in the next section, and then reinforced by a discussion of errors that have retarded, for a long time, the study of quasicrystals.
The term “quasicrystallography” was coined by its practitioners [5] , though journals have preferred to edit to “quasicrystal crystallography” [2] . The following pages, especially when read in the context of the published reviews, demonstrate that systemic errors disqualify any “quasicrystallographer” from scientific review of this subject.
Quasicrystals were discovered in 1982 and have been long discussed. The first solid, i-Al6Mn, was supposedly icosahedral in structure [10] , but see Section 3.1, and this is forbidden in crystallography for many reasons, including the fact that none of the 14 Bravais lattices allow the newly observed 5-fold rotational symmetry. Electron microscope images showed that, though the diffraction peaks were sharp, the real structure was not periodic. It was called “quasi-periodic” and the solids were referred to as “quasicrystals”. The immediate problem was four-fold: firstly, how does this structure compare with those of crystals or with amorphous materials; secondly, how does the diffraction arise; thirdly how does the pattern relate to structural measurement; and fourthly, what is the driving force that determines these unusual structures? With regard to the second of these, because of fundamental disparities, the new metallic alloys cannot follow Bragg’s law―as observed in periodic crystals and in non-periodic amorphous phases―though the scattering was called Bragg diffraction by confusion. The following summary of general features describes a theory that unravels the confusion in many ways, but especially by describing and measuring the metric that is a necessary part of structural analysis and science. We do not ask “What is a quasicrystal?” [11] . “The short answer is no one knows.” We find that with the edgesharing unit cells, with 3-dimensional indexation, with the Quasi-Bragg law, the structure is solved and a new law of physics is discovered. This follows from the multiple interplanar spacings in geometric series. The consequent sharp diffraction patterns are systematically simulated. This paper reviews the argument in condensed form.
2. General Features
The following summary of features suffices for the solution:
2.1. Structure
1) A unique unit cell that is icosahedral and extremely dense:
• With 15 close packed planes through its center;
• With 20 close packed planes on its surface;
• And with a density increase of 17% compared with the equivalent cell in the face-centered cubic phase. This is a crystalline phase that forms the matrix in rapidly quenched Al6Mn [10] [12] ;
2) With a stoichiometric alloy ratio of 6:1. This occurs on a unit cell with 12 shared surface atoms and one completely contained central atom, in this case Mn.
3) With a significant ratio of solute metal atom diameter/solvent diameter of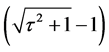 , where the golden section
, where the golden section . These diameters are consistent with the dense packing2;
. These diameters are consistent with the dense packing2;
4) With an icosahedral cell that is edge-sharing; not face sharing as in crystals. Notice that many glasses, such as amorphous silica, also have dense, edge-sharing cells; but the diffraction patterns are diffuse and circular because the sharing is by single, uncorrelated edges. By contrast, the quasicrystal cells share two or more adjacent edges, and these result in unique orientation with sharp diffraction patterns by a mechanism that is simulated.
5) With an agglomeration of cells that is represented in an ideal hierarchic structure that is uniquely icosahedral, uniquely aligned and infinitely extensive;
6) With a structure that is open to simulation.
2.2. Diffraction Pattern
1) With structural and diffraction pattern sequences that are geometric (as below);
2) With complete, simple and systematic 3-dimensional indexation of icosahedral axes and diffraction planes [1] ;
3) With 3-dimensional pattern indexation that is simple, consistent and complete;
4) With an explanation for the diffraction that is systematically, completely, and simply described by means of the Quasi-Bragg law that has been derived and is now enhanced in appendix A.1 ~ A.2.
2.3. Measurement
1) With simulated quasi-structure factors that match experimental values extraordinarily well [5] [7] ;
2) With a structure that is simulated and systematically measured without guessing [cf. [5] [13] ], and which matches both phase contrast microscopic images, and atomic dimensions;
3) With a simple demonstration of the measured metric [4] [5] , including serious consequences for image analysis (see below) and for structural analysis.
2.4. Driving Force
1) As derived above consistently, especially in sections 2.1.1 to 2.1.3;
2) With a logarithmic electron energy band structure [2] having high density of states at long wavelengths that stabilize the structure, etc.
Notice that the ‘logarithmically periodic solid’ described is the only proposed solution with a single unit cell and obvious driving force, and is the only solution that has been systematically and consistently measured. The structure is illustrated in Figure 1 viewed close to the direction of the 5-fold axis. No other method of solution is free of one or more of the blunders to be described in the next section.
3. Seven Blunders
3.1. The Data of Shechtman et al. [10] Are Not Icosahedral
Their two-fold patterns are inconsistent (Figure 2). Spatial symmetries constitute the foundation of crystallography. If Shechtman’s data were correct, the inconsistency would have extremely significant structural implications. The fact of inconsistency was (1) overlooked by quasicrystallographers for 25 years; (2) denied by many reviewers e.g. [5] ; but when occasionally admitted, claimed to be trivial [7] , in spite of their false simulations. In fact we have found, firstly, that his data are excluded by our simulations on the ideal icosahedral, hierarchic structure; and secondly that they do not match icosahedral systems other than Shechtman’s Al6Mn [citations in ref. 1]. Two assumptions are therefore fairly made: his data are mistakenly transcribed; and a fundamental feature of crystallography has passed unnoticed. The pity is that the experimental discovery is so novel.
3.2. The Diffraction Pattern Sequence Is Not Properly Fibonacci
This sequence has the following properties: each term is the sum of its two preceding terms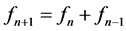 ,
,

Figure 1. Hierarchic icosahedral cluster viewed from near a 5-fold axis of rotational symmetry. Individual icosahedra are represented by golden triads constructed from golden rectangles, each having the significant length/width ratio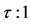 . In i-Al6Mn, the center of each golden triad locates a Mn atom surrounded, at corners, by Al atoms. The unit cell is extremely dense; the ideal structure is infinitely extensive, uniquely aligned, and uniquely icosahedral. The stretching factor is
. In i-Al6Mn, the center of each golden triad locates a Mn atom surrounded, at corners, by Al atoms. The unit cell is extremely dense; the ideal structure is infinitely extensive, uniquely aligned, and uniquely icosahedral. The stretching factor is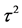 .
.
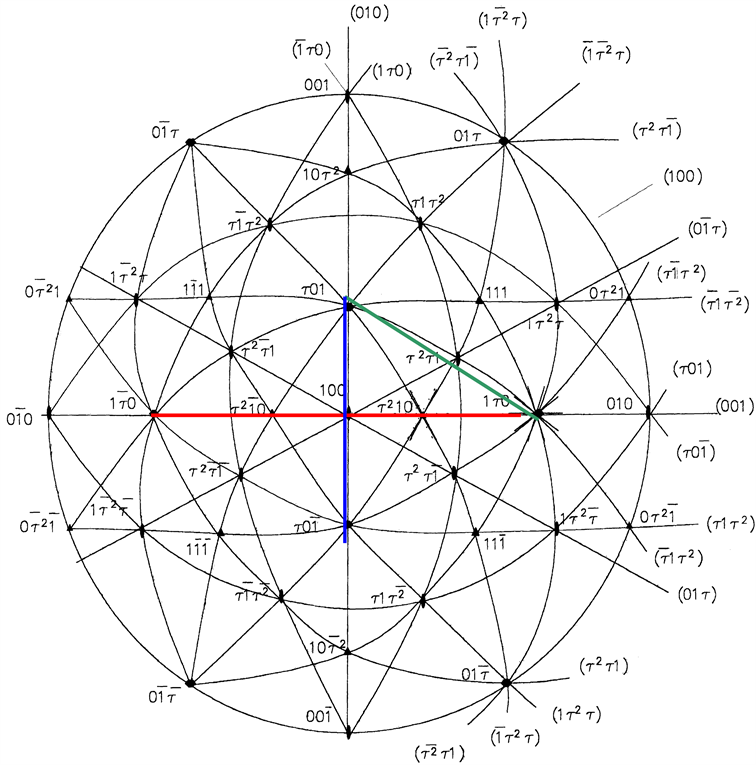
Figure 2. Icosahedral stereogram showing 5-3-2-3-5 poles along horizontal, red axis as in [10] with 5-2-5 poles on green diagonal. In the published data, the 2-fold patterns show the same parallelism with respective axes, and this is anomalous: notice, the patterns at poles 100 and τ2τ1 have the same orientation with respect to corresponding (colored) axes, since the green line is symmetrically identical to the blue line. However the vertical, blue axis with 5-2-5 poles shows that the crossed, two-fold diffraction patterns for the icosahedral structure are mutually normal, Simulations match data from other “icosahedral” alloys [1] and so confirm a transcription error; not a systematic structural anomaly in Al6Mn. Shechtman’s data are not icosahedral (Original stereogram courtesy Elsevier, [1] ).
and the ratio between consecutive terms in a series, 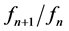 , tends to the golden section
, tends to the golden section 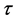 (Appendix A.2) as order
(Appendix A.2) as order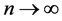 . However in the quasicrystal diffraction pattern, this ratio is the constant
. However in the quasicrystal diffraction pattern, this ratio is the constant , and so the series is the geometric series,
, and so the series is the geometric series,![]() . This fact has profound consequences for the description of the diffraction pattern whose indices are properly described in integral powers of
. This fact has profound consequences for the description of the diffraction pattern whose indices are properly described in integral powers of , as shown for poles and diffraction planes in Figure 2. Detailed illustrations of these facts are provided elsewhere [1] [2] , but nowhere else in the review literature are those details described, discussed or even cited.
, as shown for poles and diffraction planes in Figure 2. Detailed illustrations of these facts are provided elsewhere [1] [2] , but nowhere else in the review literature are those details described, discussed or even cited.
It is interesting to note, nevertheless, that the geometric series on the ratio 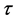 has some interesting properties in common with the Fibonacci sequence. For example, while free electron energy bands have slope 2 when plotted on logarithmic scales, quasi-Brillouin scattered electron energy bands in a quasicrystal have a negative slope half that value, −1 [2] . This is a consequence of the first of the equalities formulated in the preceding paragraph. Even so a Fibonacci series in which, by definition, the first two terms can be any variables, f1 = a; f2 = b, is too loose and inaccurate a description of the diffraction patterns in quasicrystals. In this application, f2 is strictly constrained:
has some interesting properties in common with the Fibonacci sequence. For example, while free electron energy bands have slope 2 when plotted on logarithmic scales, quasi-Brillouin scattered electron energy bands in a quasicrystal have a negative slope half that value, −1 [2] . This is a consequence of the first of the equalities formulated in the preceding paragraph. Even so a Fibonacci series in which, by definition, the first two terms can be any variables, f1 = a; f2 = b, is too loose and inaccurate a description of the diffraction patterns in quasicrystals. In this application, f2 is strictly constrained: , and the series ratios
, and the series ratios 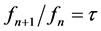 for all n. The diffraction pattern spacings are then geometric: a,
for all n. The diffraction pattern spacings are then geometric: a, 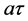 ,
, ![]() ,
, ![]() ,··· This geometric pattern is moreover common to both the hierarchic model, and to its set of interplanar spacings. Illustrations of the last are given elsewhere [5] [7] for the ideal hierarchic structure and they are commonly seen in electron micrographs.
,··· This geometric pattern is moreover common to both the hierarchic model, and to its set of interplanar spacings. Illustrations of the last are given elsewhere [5] [7] for the ideal hierarchic structure and they are commonly seen in electron micrographs.
3.3. Quasicrystals Are Not 6-Dimensional
In real space, the structure is unambiguously 3-dimensional. However for reasons given in the previous section, neither the structure nor the diffraction pattern are 6-dimensional in any sense that can survive Occam’s razor: dimensions “should not be multiplied without necessity”. Unfortunately, unphysical dimensionality is the most strongly held tenet of quasicrystallography [5] [13] [14] .
A reader will easily find a simple understanding for their widespread belief in 6-dimensional quasicrystals: indexation, for quasicrystallographers, is based on a double Fibonacci series construction, though the series is, in fact, simply three dimensional and geometric – as in real life. An illustration can be given for the relationship between those Fibonacci sequences and the single geometric series, base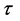 , that is proper in quasicrystals. This geometric series G can be written as the sum of two Fibonacci series, F1, F2, one of them multiplied by
, that is proper in quasicrystals. This geometric series G can be written as the sum of two Fibonacci series, F1, F2, one of them multiplied by 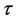 [5] . As an example, it is shown that the second term of the geometric series is written
[5] . As an example, it is shown that the second term of the geometric series is written![]() , f1 and f2 being the first two terms in the same Fibonacci series. Furthermore, the golden section is an irrational number, which is why G is not linearly harmonic (as quoted in Section 3.6 below, but typical only in crystals).
, f1 and f2 being the first two terms in the same Fibonacci series. Furthermore, the golden section is an irrational number, which is why G is not linearly harmonic (as quoted in Section 3.6 below, but typical only in crystals).
As in the stereogram, geometric, 3-dimensional indexation is easily and completely represented, without obfuscation [1] [2] [5] [7] [15] . What has to be understood, as is done through simulation, is the diffractive effect that is due to sets of planes that are spaced by orders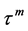 ,
,  , m integral and 3-dimensional. The doubled sequence on F has led to confusion with 6 dimensions.
, m integral and 3-dimensional. The doubled sequence on F has led to confusion with 6 dimensions.
3.4. The Diffraction Is Not Bragg Diffraction
This law applies to periodic crystals, as it does to amorphous materials. In each case, the scattering is specular and is commonly represented on 2-dimensional ray diagrams. The scattering is constrained by the Ewald sphere construction, and also by absorption, crystal orientation and other features. Such features vary according to applications in X-ray optics or in electron or neutron optics etc. In particular, electron diffraction relaxes the Ewald sphere constraint [16] supplying instead a deviation parameter that partly determines scattering and absorption. Simulations of scattering from crystals are typically 3-dimensional. In quasicrystals, however, the differences become so radical, that the diffraction ceases to be describable as Bragg diffraction except by extreme use of the Humpty-Dumpty principle3. In the first place, quasicrystals contain multiple interplanar spacings that are all active in each diffractive event. Simulations from an extensive, ideal, hierarchic, icosahedral quasicrystal show that Bragg’s law is transmuted from ![]() for scattering of X-rays of wavelength
for scattering of X-rays of wavelength 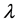 from a crystal with interplanar spacing d at Bragg angle
from a crystal with interplanar spacing d at Bragg angle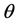 . The orders are linear in n. In quasicrystals, structure factors calculated by Bragg’s law are all zero. The new Quasi-Bragg law becomes
. The orders are linear in n. In quasicrystals, structure factors calculated by Bragg’s law are all zero. The new Quasi-Bragg law becomes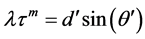 , where d' is a corrected quasi interplanar spacing
, where d' is a corrected quasi interplanar spacing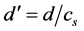 ; where the compromise spacing effect
; where the compromise spacing effect 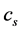 is discovered to be constant for all quasi-structure factors; and where the Quasi-Bragg angle
is discovered to be constant for all quasi-structure factors; and where the Quasi-Bragg angle 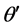 differs from the Bragg angle in crystals, chiefly because of the multiple interplanar spacings. The order m is now geometric. Every variable except wavelength is different in the Quasi-Bragg law and even the constant 2 becomes unity. This occurs because of the approximately half-integral nature of the interplanar sequences [5] , especially at low m. The simulated quasi-structure factors match experimental values extraordinarily well [5] [7] . A simple illustration of the special diffraction, that is described in terms of calculated quasi-Bloch waves, is available elsewhere [3] [5] [9] .
differs from the Bragg angle in crystals, chiefly because of the multiple interplanar spacings. The order m is now geometric. Every variable except wavelength is different in the Quasi-Bragg law and even the constant 2 becomes unity. This occurs because of the approximately half-integral nature of the interplanar sequences [5] , especially at low m. The simulated quasi-structure factors match experimental values extraordinarily well [5] [7] . A simple illustration of the special diffraction, that is described in terms of calculated quasi-Bloch waves, is available elsewhere [3] [5] [9] .
Many consequences follow an inadequate understanding of the special diffraction; two (in imaging and in structural analysis) will be described below as illustrations. Quasicrystallographers have failed to understand or explain the special diffraction in quasicrystals that relates to the multiple interplanar spacings: multi-dimensionality multiplies only confusion; the interplanar spacings are indeed evident in phase-contrast electron microscopy e.g. [17] . The practitioners resort to over-economical and erroneous guesses (or “choices”), without measurement [5] . The multiple interplanar spacings in geometric series in quasicrystals cause a new law in physics: the Quasi-Bragg law. Where Bragg’s law transformed a crystal lattice onto a 3-dimensional reciprocal lattice; the Quasi-Bragg law transforms a 3-dimensional geometric pattern onto an hierarchic structure.
3.5. HRTEM Does Not Image Atoms
High resolution transmission electron microscopy (HRTEM) is complicated science that is typically ambiguous and that is easily misrepresented [16] . The contrast results from interference of Bloch waves generated during transmission through a crystalline foil in an electron microscope. The contrast is strongly dependent on specimen thickness, specimen orientation, defocus, estimates of absorption rates of individual Bloch waves, etc. When it can be proved that the Bloch waves peak on atomic columns, as is common in crystals, then the interference can be interpreted as an image of the columns. Even so, significant interpretation requires systematic simulation of through-focal series in multiple images, etc. However, without a proper theory of diffraction, no HR image is of any significance. In fact diffraction simulations, including the compromise spacing effect [7] that results from the multiple interplanar spacings and the measured metric, demonstrate that the Bloch waves do not peak on atomic columns. HRTEM does not therefore image atoms in quasicrystals. Any interpretation that is based on structure from HR images is misrepresented.
3.6. Fourier Transforms Are Misleading
How should a crystallographer interpret real structure from a diffraction pattern that he does not understand? An example is given in the following review [5] :
“We know that for every reflection with index H and its higher harmonics with indices nH, there exists a periodic average structure (PAS) with period dH which has to be used in Bragg’s equation. Then it can be applied as usual. The scaling symmetry by powers of 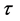 of the diffraction pattern, which is a Fourier module of rank n (n > 3) does not need to enter Bragg’s equation; we just have to choose dH of the respective scales PAS properly.”
of the diffraction pattern, which is a Fourier module of rank n (n > 3) does not need to enter Bragg’s equation; we just have to choose dH of the respective scales PAS properly.”
The trouble is, he doesn’t know how to make the proper choice, so his simulation is without measurement, without consistency and without significance. Moreover, what mental confusion allows a “periodic average structure” in a “non-periodic material”? Furthermore, his “harmonics” are not observed. If there are harmonics, they are in geometric space, but only sound visual inspection proves it. Any interpretation that lacks the measured metric is unphysical.
Worse still, is the misallocation of effort. Fourier transform analysis hides defects where these are of the greatest significance for structure, especially in rapidly quenched material, like Shechtman’s. That is why sterogram’s such as that in Figure 2 is of greater significance: in providing a perspective for the diffraction they enable dark field imaging of the defects.
3.7. Multiple Cells Higgledy Piggledy
Mathematically, it is as easy to multiply cells as to multiply dimensions, but neither contributes to understanding why and how quasicrystals form. Amorphous silica can be constructed from an infinite number of unit cells. Quasicrystallographers typically contrive cells that could contribute to icosahedral structure [18] ; but they are not able to measure them and narrow down to a solution. In crystallography, only one cell is allowed, and this in periodic array with a precise symmetry. Typically, chemical conditions during formation determine the symmetry, the unit cell, and therefore the structure. The conditions include cooling rate.
Multiplicity of cells fails many requirements of acceptable theory: it does not explain stoichiometry in this type of alloy; it does not explain peculiar atomic sizes; it does not reveal the driving force for these unusual materials. Only the ideal of logarithmic periodicity satisfies these requirements. Crystallography abhors multiple unit cells!
4. Conclusion
The structure of icosahedral quasicrystals is solved. It depends on an icosahedral unit cell that is extremely dense and that is edge-sharing. By contrast, seven quasi-conventional blunders are described: Shechtman’s data are not icosahedral; the diffraction pattern is not Fibonacci; quasicrystals are not 6-dimensional; there is no Bragg diffraction; HRTEM does not image atoms; Fourier transform analysis, without the measured metric, is misleading; and crystallography abhors multiple unit cells. The Quasi-Bragg law is a new law in physics.
References
- Bourdillon, A.J. (2013) Micron, 51, 21-25. http://dx.doi.org/10.1016/j.micron.2013.06.004
- Bourdillon, A.J. (2009) Solid State Communication, 149, 1221-1225. http://dx.doi.org/10.1016/j.ssc.2009.04.032
- Bourdillon, A.J. (2011) Logarithmically Periodic Solids, Nova Science.
- Bourdillon, A.J. (2011) Logarithmically Periodic Solids―Properties, Evidence and Uncertainties. In: Puckermann, B.E., Ed., Quasicrystals: Types, Systems, and Techniques, Nova Science.
- Bourdillon, A.J. (2012) Metric, Myth and Quasicrystals.
- Bourdillon, A.J. (2010) Quasicrystals’ 2D Tiles in 3D Superclusters.
- Bourdillon, A.J. (2009) Quasicrystals and Quasi Drivers.
- (2013) American Physical Society March Meeting, Baltimore, 18-23 March 2013, Session W43. In Response to Journals, the Meeting Instructed the Speaker: “Be aggressive;” “Remove the kid-gloves,” “Add insult”.
- (2013) Quasicrystals at the American Physical Society March Meeting. http://www.youtube.com/watch?v=xD30KF93qio
- Shechtman, D., Blech, I., Gratias, D. and Cahn, J.W. (1984) Physical Review Letters, 53, 1951-1953. http://dx.doi.org/10.1103/PhysRevLett.53.1951
- Senechal, M. (2006) Notices to the American Mathematical Society, 3, 886-997.
- Bourdillon, A.J. (1987) Philosophical Magazine Letters, 55, 21-26. http://dx.doi.org/10.1080/09500838708210435
- Steurer, W. (2004) Zeitschrift für Kristallographie, 219, 391-446. http://dx.doi.org/10.1524/zkri.219.7.391.35643
- Steurer, W. and Deloudi, S. (2008) Acta Crystallographica, A64, 1-11.
- Bourdillon, A.J. (2013) Quasicrystallography. www.UHRL.net
- Hirsch, P., Howie, A., Nicholson, R.B., Pashley, D.W. and Whelan, M.J. (1977) Electron Microscopy of Thin Films. 2nd Edition, Krieger, New York.
- Bursill, L.A. and Peng, J.L. (1985) Nature, 316, 50-51. http://dx.doi.org/10.1038/316050a0
- Takakura, H., Gomez, C.P., Yamamoto, A., De Boisieu, M. and Tsai, A.P. (2006) Nature Materials, 61, 58-63.
- Huntley, H.E. (1970) The Divine Proportion, Dover.
Appendix
A.1. Fourier Summations on Geometric Series In grating optics and Fraunhofer diffraction, Fourier transforms of the grating are used to describe diffraction patterns observed in the image plane. In crystal optics, it is often possible to approximate atoms to point scatterers and so apply Fourier series to the analysis. We did this before in simulations of quasi-structure factors. The calculations were performed in 3-dimensions over a truncated and ideal hierarchic model that is, in principle, infinitely extensive. Now we show how the method can be used to understand quasi-Bragg diffraction on atoms in linear geometric series.
Start with the Quasi-Bragg law described earlier,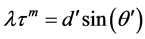 . Proceed to simulate quasi structure factors in the centrosymmetric hierarchic model by following the crystalline case, where a structure factor Fhkl for a reflection with Miller indices h, k, l, is written:
. Proceed to simulate quasi structure factors in the centrosymmetric hierarchic model by following the crystalline case, where a structure factor Fhkl for a reflection with Miller indices h, k, l, is written:
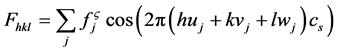 (A1)
(A1)
summed over atoms j, each with atomic scattering amplitude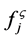 , on coordinates uj, vj and wj,, where the superscript
, on coordinates uj, vj and wj,, where the superscript 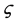 identifies the chemical species on the site: either Al or Mn. Notice the compromise spacing effect metric cs that has unit value in crystals, but that has a smaller measured value in quasicrystals because the multiple interplanar spacings are here non-uniform and geometric. Then the quasi-Miller indices
identifies the chemical species on the site: either Al or Mn. Notice the compromise spacing effect metric cs that has unit value in crystals, but that has a smaller measured value in quasicrystals because the multiple interplanar spacings are here non-uniform and geometric. Then the quasi-Miller indices 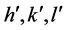 have typical values in individual powers of
have typical values in individual powers of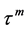 ; while the atomic locations
; while the atomic locations 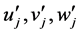 are expressed in values belonging to powers
are expressed in values belonging to powers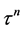 , e.g.
, e.g.  where the an factors are integral values that express the number of times a particular interplanar space is contained in uj. The factors are inherent in the simulations cited earlier. Quasi structure factors, calculated for superclusters up to order 6, with 108 atomic sites, match experimental values.
where the an factors are integral values that express the number of times a particular interplanar space is contained in uj. The factors are inherent in the simulations cited earlier. Quasi structure factors, calculated for superclusters up to order 6, with 108 atomic sites, match experimental values.
Now we introduce a further feature that is the evident result of many calculations. We have found the line width of quasi-structure factors to be dependent on sample sizes used in simulations. For example in a cluster of ~100 atoms the line width is ~5% of the quasi-Bragg angle; reducing to 0.005% in the supercluster order 6. The most probable reason for the systematic trend is the oscillatory behavior in the cosine term in Equation (A1).
We now proceed to further details in the crystallography of quasicrystals. Begin by noticing the octahedral subgroup within the icosahedral point group symmetry. This is enabling, both for the 3-dimensional indexation, while it also allows us to write for an interplanar spacing 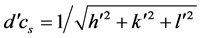 since
since 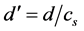 with the measured metric, and where the unit of length is the edge length of the icosahedral unit cell. Simplifying to one dimension by choosing
with the measured metric, and where the unit of length is the edge length of the icosahedral unit cell. Simplifying to one dimension by choosing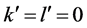 , expand equation A1 in series:
, expand equation A1 in series:
 , (A2)
, (A2)
with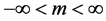 ,
, 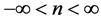 ,
,  , m, n, p all integral. As before, the factor
, m, n, p all integral. As before, the factor  has replaced
has replaced 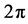 in (A1) because of the approximately halfintegral values of
in (A1) because of the approximately halfintegral values of  at low powers [5] . Notice that the second term in the square brackets is oscillatory. This explains the narrowing of quasi-structure factor line widths previously remarked. In large specimens, the second term therefore sums approximately to zero, and we are left with a structure factor in Fourier series that depends on the number of atoms, including their scattering powers
at low powers [5] . Notice that the second term in the square brackets is oscillatory. This explains the narrowing of quasi-structure factor line widths previously remarked. In large specimens, the second term therefore sums approximately to zero, and we are left with a structure factor in Fourier series that depends on the number of atoms, including their scattering powers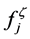 . The result is typical, and the metric is consistently measured already in the 3-dimensional quasi-structure factor calculations. The metric correlates with the quasi-Bragg angle and corresponds to the variety of interplanar spacings found in the ideal hierarchic model.
. The result is typical, and the metric is consistently measured already in the 3-dimensional quasi-structure factor calculations. The metric correlates with the quasi-Bragg angle and corresponds to the variety of interplanar spacings found in the ideal hierarchic model.
In quasicrystals, linearly periodic electromagnetic waves are scattered by atoms in an approximately hierarchic structure having logarithmic periodicity, in such a way that the resulting diffraction pattern is geometric as simulated.
A.2. Geometric and Fibonacci Series Compared
Table A.1 illustrates the source of confusion for a 6-dimensional construction of a three dimensional structure
Table A.1 . Comparison between Fibonacci series (not observed) and Geometric series (as observed).
with logarithmic periodicity. Start with the simplest Fibonacci sequence based on 0 and 1 (column 1) then calculate the ratios between consecutive terms. Notice that they vary about τ (column 2); that they tend to τ at high order; and that the quasicrystal diffraction series that is observed is not Fibonacci because it lacks the property of varying ratios [19] . Next set up a Fibonacci series that starts with the ratio τ by means of initial terms 1 and τ (column 3). Calculate sequential ratios and notice they are constant τ, the same as the first term. The observed constant ratios in quasicrystal diffraction patterns are a property of the geometric series. This is firmly three dimensional. It is also the sum of two Fibonacci series on integral bases (column 2), with one of them having the irrational number τ as multiplier. The diffraction series can then be indexed using 6 numbers, though three of them are in fact redundant. The quasicrystal structure is firmly three dimensional and is simply comprehensible in terms of classical crystallography with the extremely dense, edge-sharing, unit cell. In this context, 3-dimensional indexation is important because it opens analysis to the range of techniques established in classical crystallography. The first of these techniques is the quasi-structure factors and measured metric.
NOTES

1see especially the response to the section editor of Acta. Cryst. in ref 5?

2Along with layered types of quasicrystal having reduced symmetry, more complex types have been found with modified structures, but they can all be understood by relation to the more symmetric icosahedral structure that is described here.

3“When I use a word… it means what I choose it to mean—neither more nor less” Dodgson CL, Alice through the Looking Glass.


