Journal of Modern Physics
Vol.3 No.11(2012), Article ID:24884,5 pages DOI:10.4236/jmp.2012.311228
Study of the EMC Effect for 27Al, 56Fe, 63Cu, and 107Ag Nuclei
Department of Physics, University of Mohaghegh Ardabili, Ardabil, Iran
Email: *Zolfagharpour@uma.ac.ir
Received August 16, 2012; revised September 18, 2012; accepted September 29, 2012
Keywords: Structure Function; Deep Inelastic Scattering; The EMC Effect
ABSTRACT
In this paper the EMC effect for 27Al, 56Fe, 63Cu, and 107Ag nuclei are investigated with oscillator model. In this model has been assumed that nucleons in each level are affected by different mean field, so we use parameter having relation with radius of each level. Therefore; this assumption causes that extracted data for average binding energy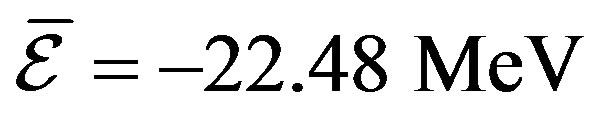 ,
,  ,
, 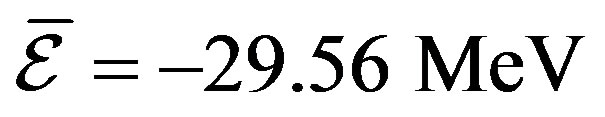 , and
, and 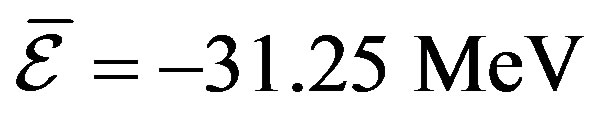 are considered for 27Al, 56Fe, 63Cu, and 107Ag nuclei, respectively. Achieving results have agreement with experimental data.
are considered for 27Al, 56Fe, 63Cu, and 107Ag nuclei, respectively. Achieving results have agreement with experimental data.
1. Introduction
In 1983, when the European Muon Collaboration (EMC) reported [1] their measurement of the ratio of the cross sections per nucleon of iron to deuterium, they realized that the ratios were clearly different from unity. For explaining this effect many theories have been expressed [2-4], but each of them just could explain in restricted x range. Akulinichev et al., [2] explained this effect base on conventional nuclear model and used the harmonic oscillator model with considering constant for different nuclei. They showed interaction between nucleons could be explained with considering the Fermi motion and the binding energy in medium x ranges. These effects have major role in deep inelastic scattering. A. Thomas et al., [3] have revealed the EMC effect results, in the conventional nuclear theory, with considering different masses for nucleons in different shells which the EMC effect could be explained, so this subject encouraged us to suppose that nucleons in different shells are affected by different mean field. Therefore, we study the EMC effect in range 0.3 < x < 0.8 for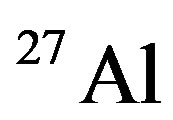 ,
, 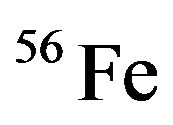 ,
, 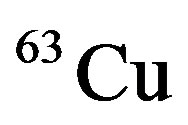 , and
, and 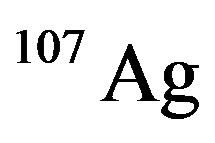 nuclei with supposing to consider the different oscillatormodel parameters for different shells, which have related to their root mean square radius [5]. In addition, we use GRV free neutron and proton structure functions [6] which have good agreement with experimental data, in conventional nuclear model. The proton and neutron structure function are different from each other, so in these nuclei that the number of proton and neutron structure are different can be suitable in x < 0.8 ranges.
nuclei with supposing to consider the different oscillatormodel parameters for different shells, which have related to their root mean square radius [5]. In addition, we use GRV free neutron and proton structure functions [6] which have good agreement with experimental data, in conventional nuclear model. The proton and neutron structure function are different from each other, so in these nuclei that the number of proton and neutron structure are different can be suitable in x < 0.8 ranges.
2. The Nucleus Structure Function
The structure functions for charged lepton scattering from a nucleon are related to cross section by:
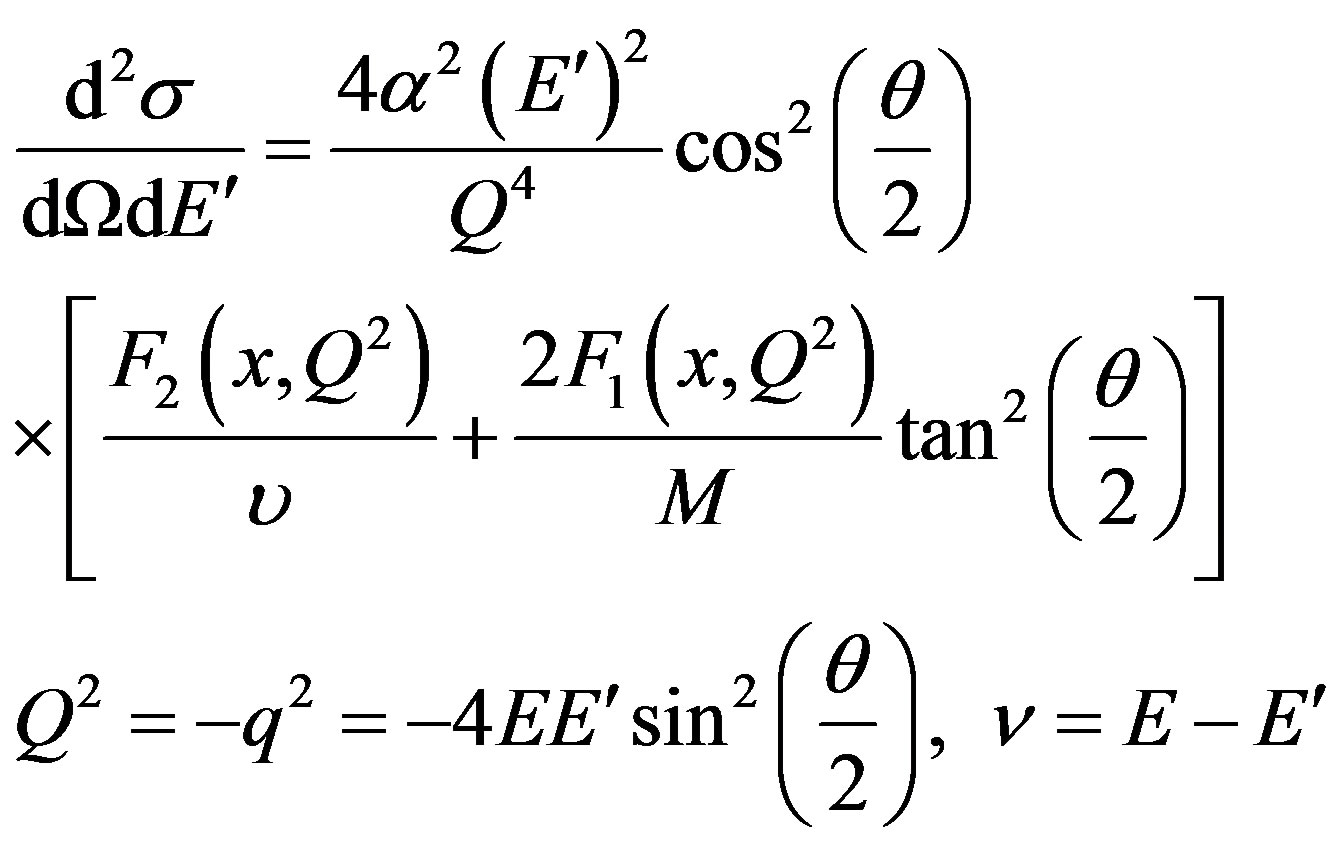 (1)
(1)
where 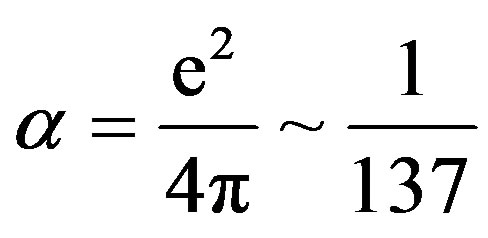 is the fine structure constant, fourmomentum transfer squared is
is the fine structure constant, fourmomentum transfer squared is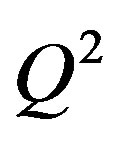 . Initial and scattered lepton energies are E and
. Initial and scattered lepton energies are E and , respectively. Energy of the virtual photon is
, respectively. Energy of the virtual photon is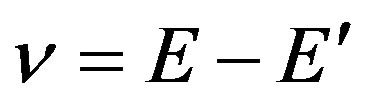 , and
, and 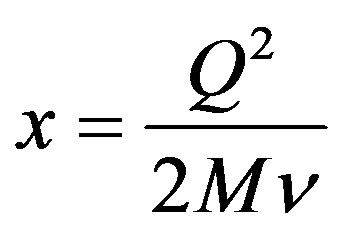 is Bjorken scaling variable.
is Bjorken scaling variable. 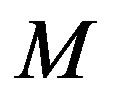 is the nucleon rest mass.
is the nucleon rest mass.  is the detected lepton scattering angle.
is the detected lepton scattering angle. 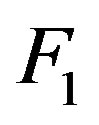 and
and 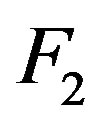 are the deep inelastic structure functions.
are the deep inelastic structure functions.
The nucleus structure function is defined by the sum of structure functions of constituted nucleons inside the nucleus, which is defined as [8]:
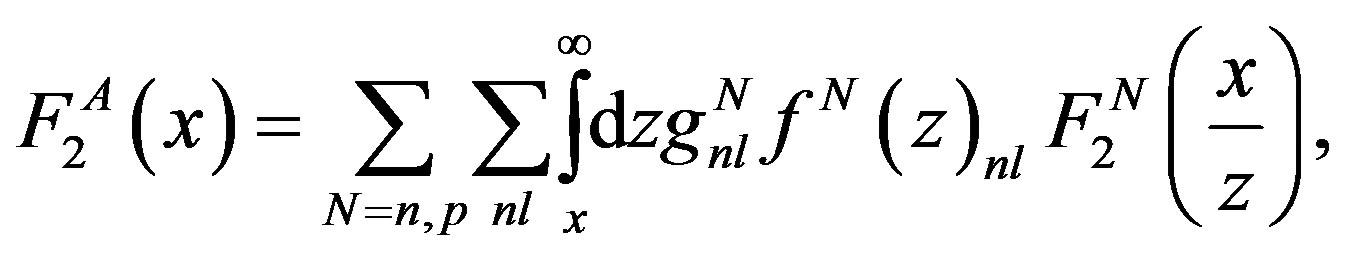 (2)
(2)
where the first sum is over proton and neutron cases. The second sum is over the quantum number of states. The 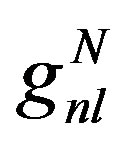 is the occupation number of energy level
is the occupation number of energy level 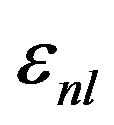 for proton
for proton 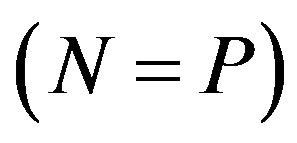 and neutron
and neutron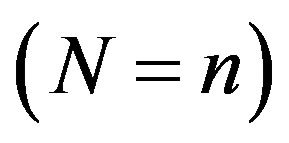 . Considered
. Considered 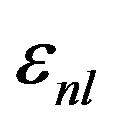 for studied nuclei are expressed in Table 1. Nucleon distribution function inside the nucleus defines as:
for studied nuclei are expressed in Table 1. Nucleon distribution function inside the nucleus defines as:
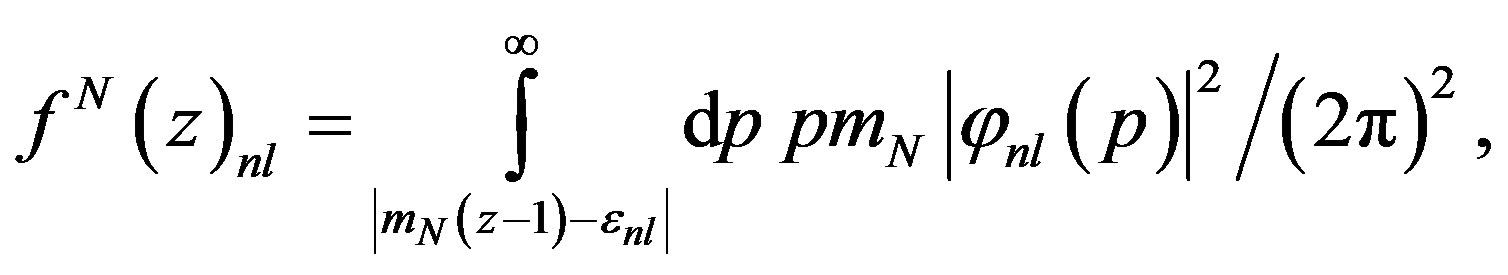 (3)
(3)
where 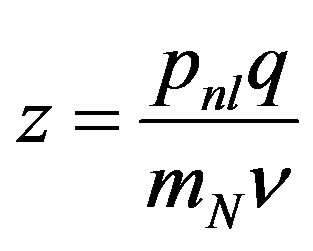 is for free nucleon. The effects of the momentum and energy distribution of the nucleon in the nucleus are included in Equation (3) through
is for free nucleon. The effects of the momentum and energy distribution of the nucleon in the nucleus are included in Equation (3) through  and
and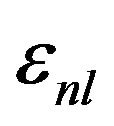 , respectively. The magnitude nuclear binding energy
, respectively. The magnitude nuclear binding energy 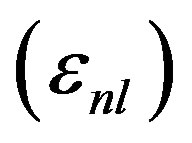 mainly effects the structure functions in the intermediate x region. Function
mainly effects the structure functions in the intermediate x region. Function 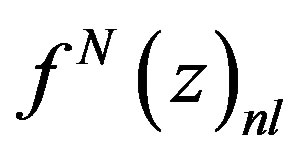 describes momentum, and energy distribution of nucleons inside nucleus, also satisfies the normalization rule:
describes momentum, and energy distribution of nucleons inside nucleus, also satisfies the normalization rule:
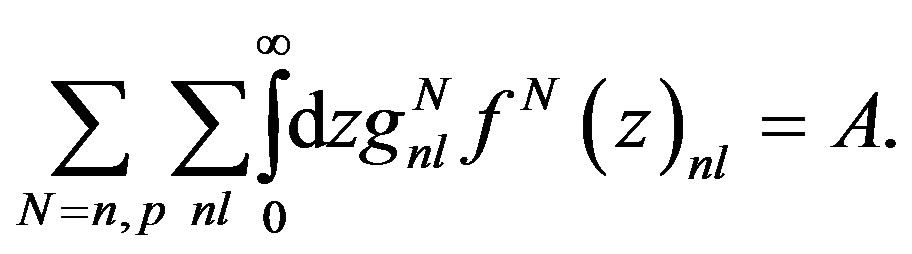 (4)
(4)
If all contributions such as gluons and sea quarks are considered then the nucleon structure function satisfies sum rule:
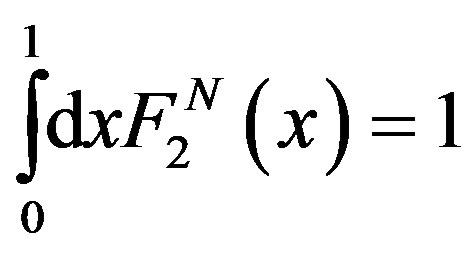 (5)
(5)
The radius of each shell could be expressed as below formula:
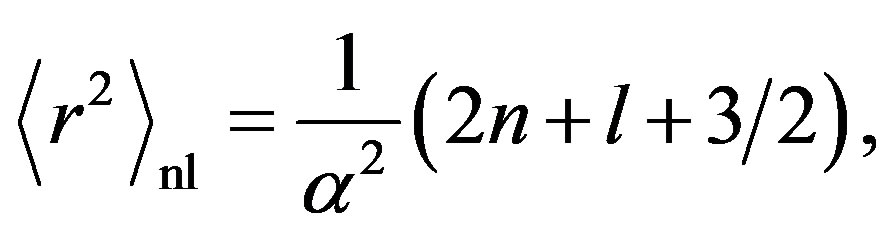 (6)
(6)
where 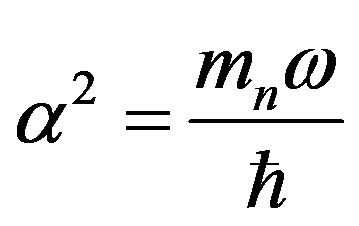 and in the natural unite we have:
and in the natural unite we have:
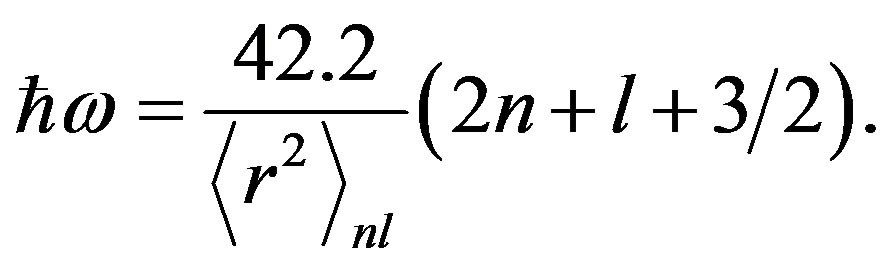 (7)
(7)
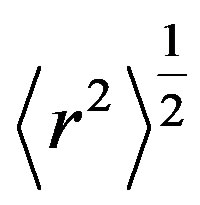 and
and  express according to Fermi and MeV unit, respectively. The calculated data for
express according to Fermi and MeV unit, respectively. The calculated data for 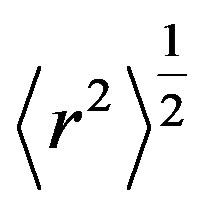 and
and
 are expressed in Table 2.
are expressed in Table 2.
According to [2] nucleon distribution function inside nuclei is considered by below formula:
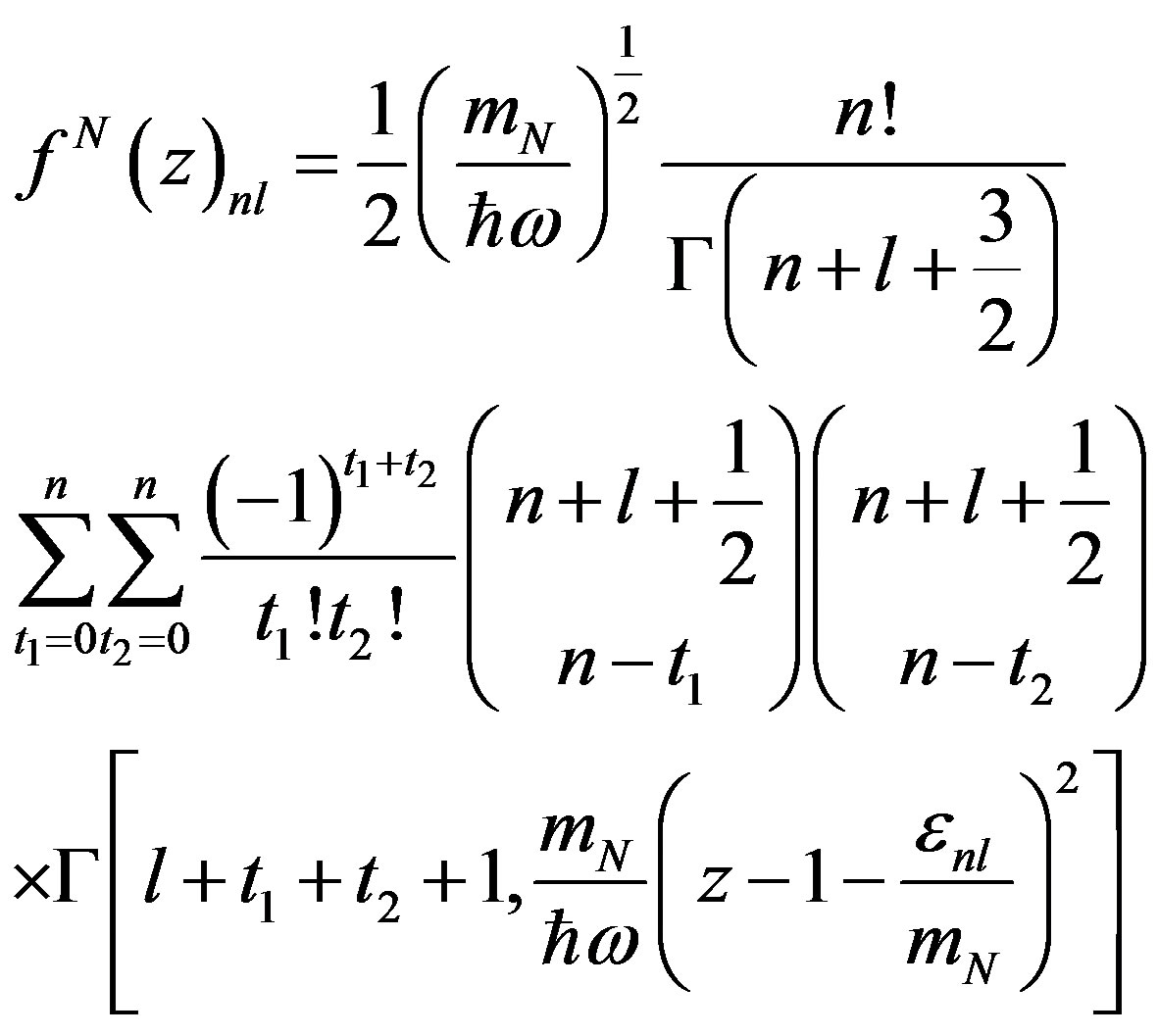 (8)
(8)
Free proton and neutron structure, 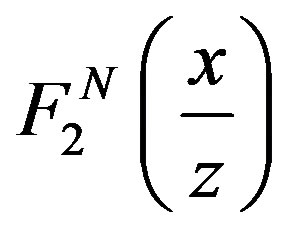 , have been used from M. Gluck et al., [6]. our calculations are based on GRV free proton and neutron structure functions [6], and we ignored the contribution of strange quark. The free proton and neutron structure functions
, have been used from M. Gluck et al., [6]. our calculations are based on GRV free proton and neutron structure functions [6], and we ignored the contribution of strange quark. The free proton and neutron structure functions
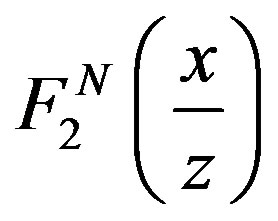 , in Figure 1 base on [6], are compared with free nucleon structure function in ref [2] and experimental data.
, in Figure 1 base on [6], are compared with free nucleon structure function in ref [2] and experimental data.
3. The EMC Effect
The EMC ratios for nuclei have calculated by [1]:
 . (9)
. (9)
The EMC ratios for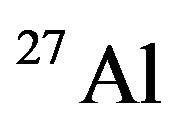 ,
,  ,
, 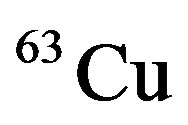 , and
, and 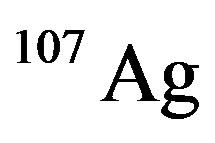 nuclei are plotted in Figures 2-5, respectively. From exposed results in these figures, we obviously could see that the plotted curves have good agreement with experimental data. Also, the deformation of bonded nucleon structure function could be defined by [8]:
nuclei are plotted in Figures 2-5, respectively. From exposed results in these figures, we obviously could see that the plotted curves have good agreement with experimental data. Also, the deformation of bonded nucleon structure function could be defined by [8]:
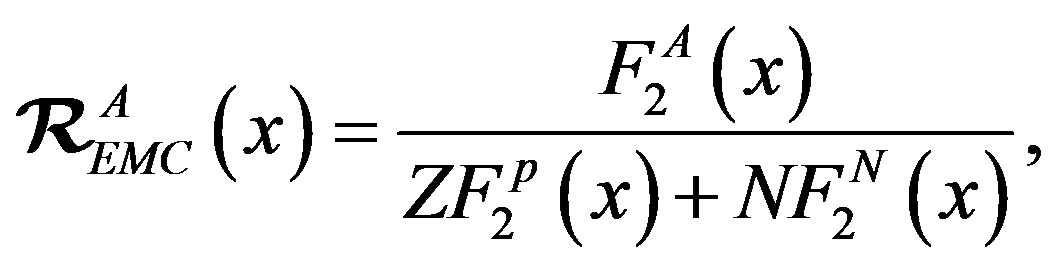 (10)
(10)
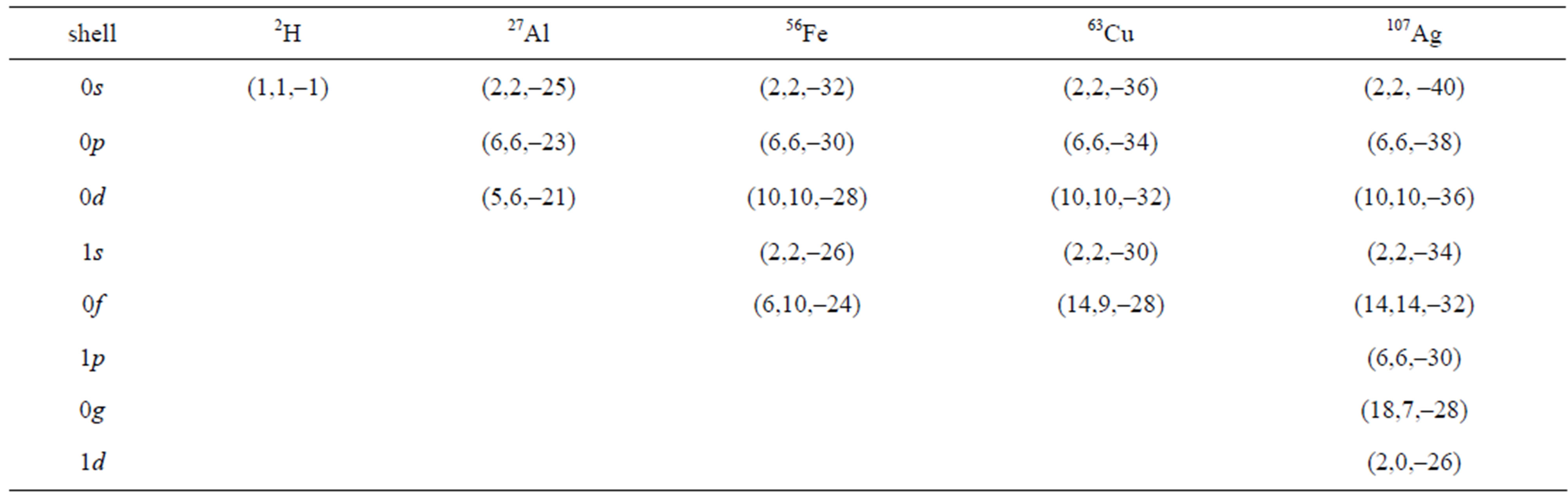
Table 1. Brackets contain 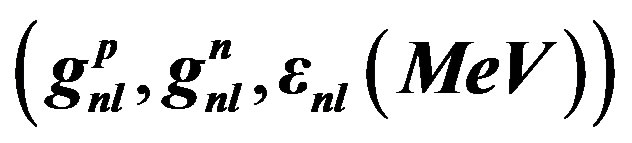 for related shell.
for related shell.

Table 2. Brackets contain 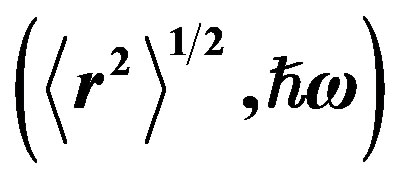 for studied nuclei that oscillator-model parameter
for studied nuclei that oscillator-model parameter 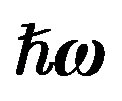 calculated from Equation (7).
calculated from Equation (7). 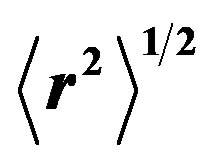 is taken from [7] for each level.
is taken from [7] for each level.
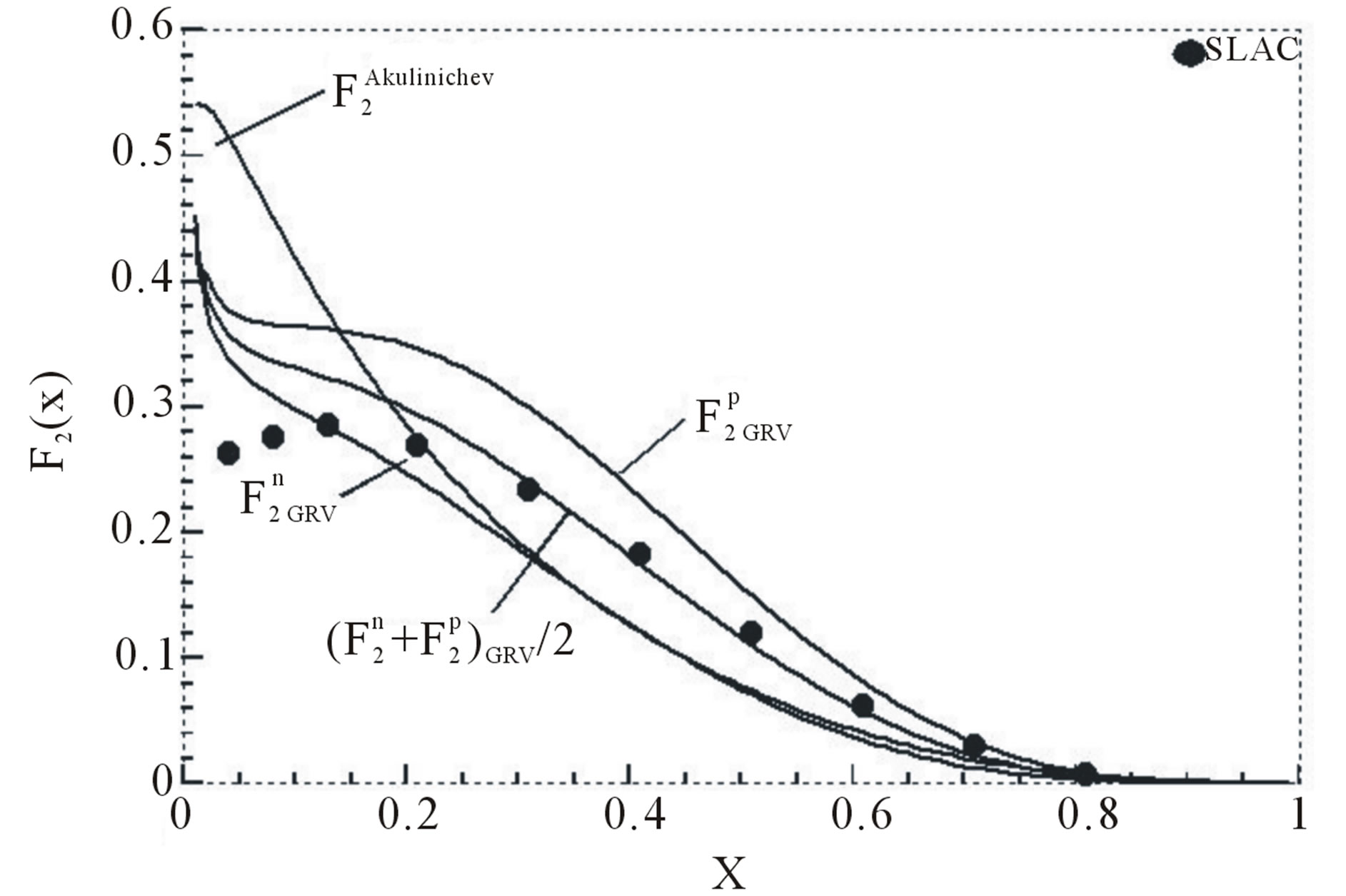
Figure 1. Free proton and neutron structure functions base on GRV model [6], without considering the contribution of strange quark, that are compared with the free nucleon structure function, which were proposed by Akulinichev et al., [2]. Experimental data have been taken from [9].
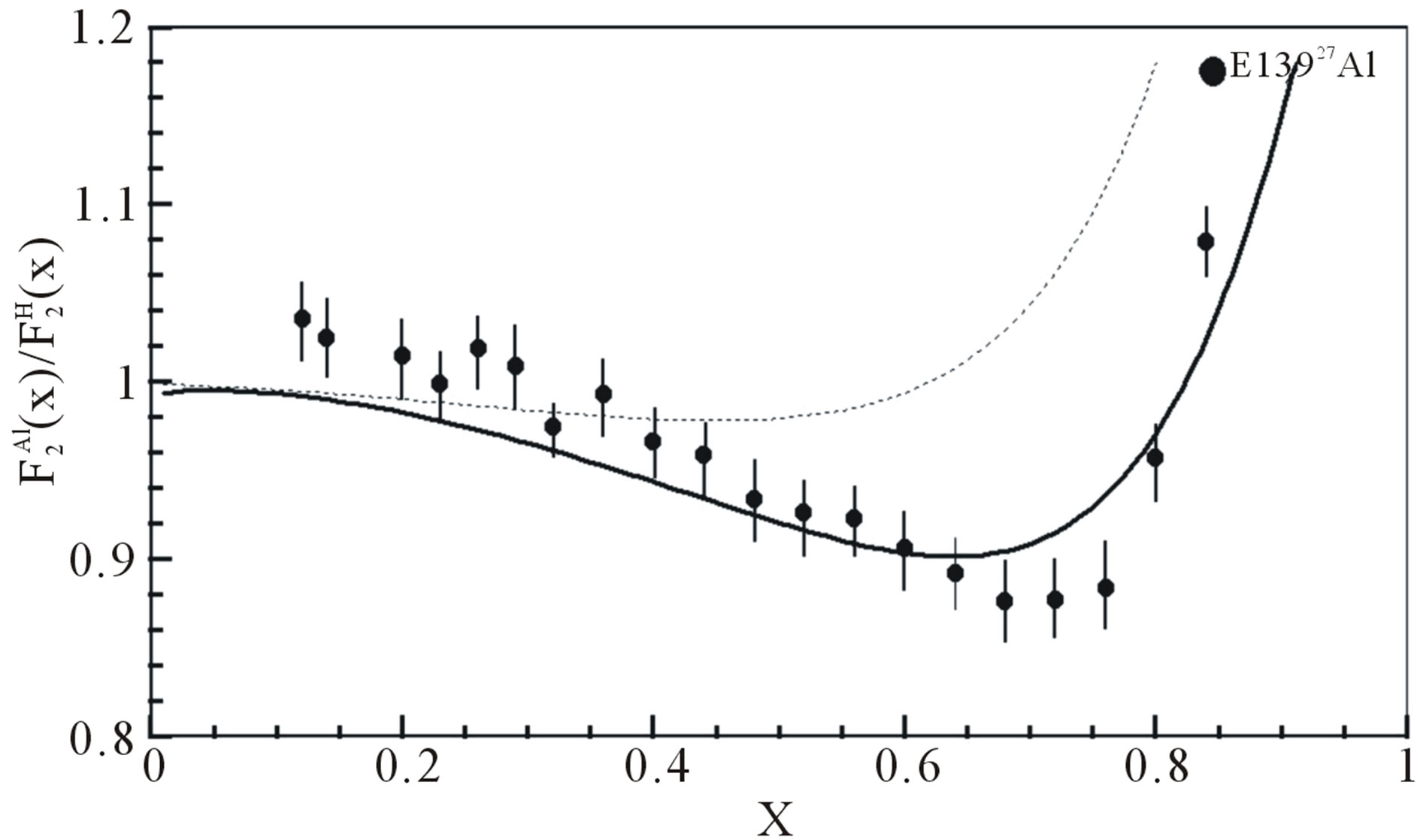
Figure 2. EMC ratio for 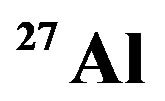 nucleus are plotted by using Equation (9), we used
nucleus are plotted by using Equation (9), we used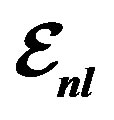 ,
, 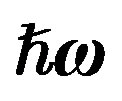 and
and 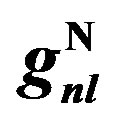 from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely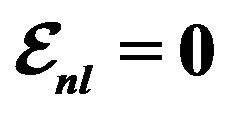 . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
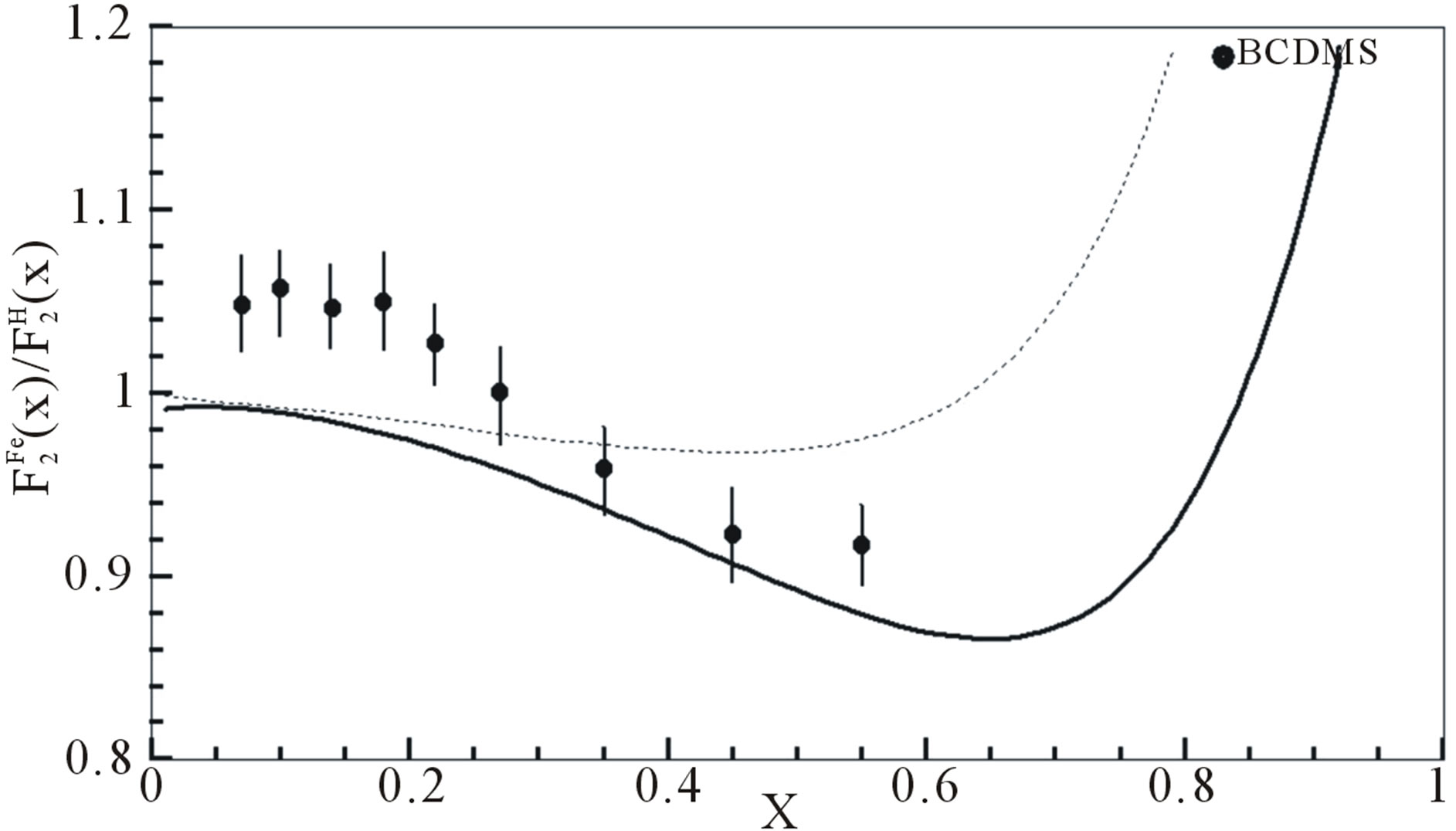
Figure 3. EMC ratios for, 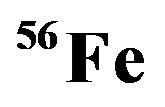 nucleus are plotted by using Equation (9), we used
nucleus are plotted by using Equation (9), we used ,
, 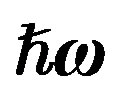 , and
, and 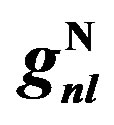 from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely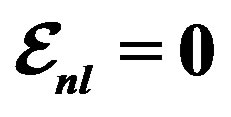 . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
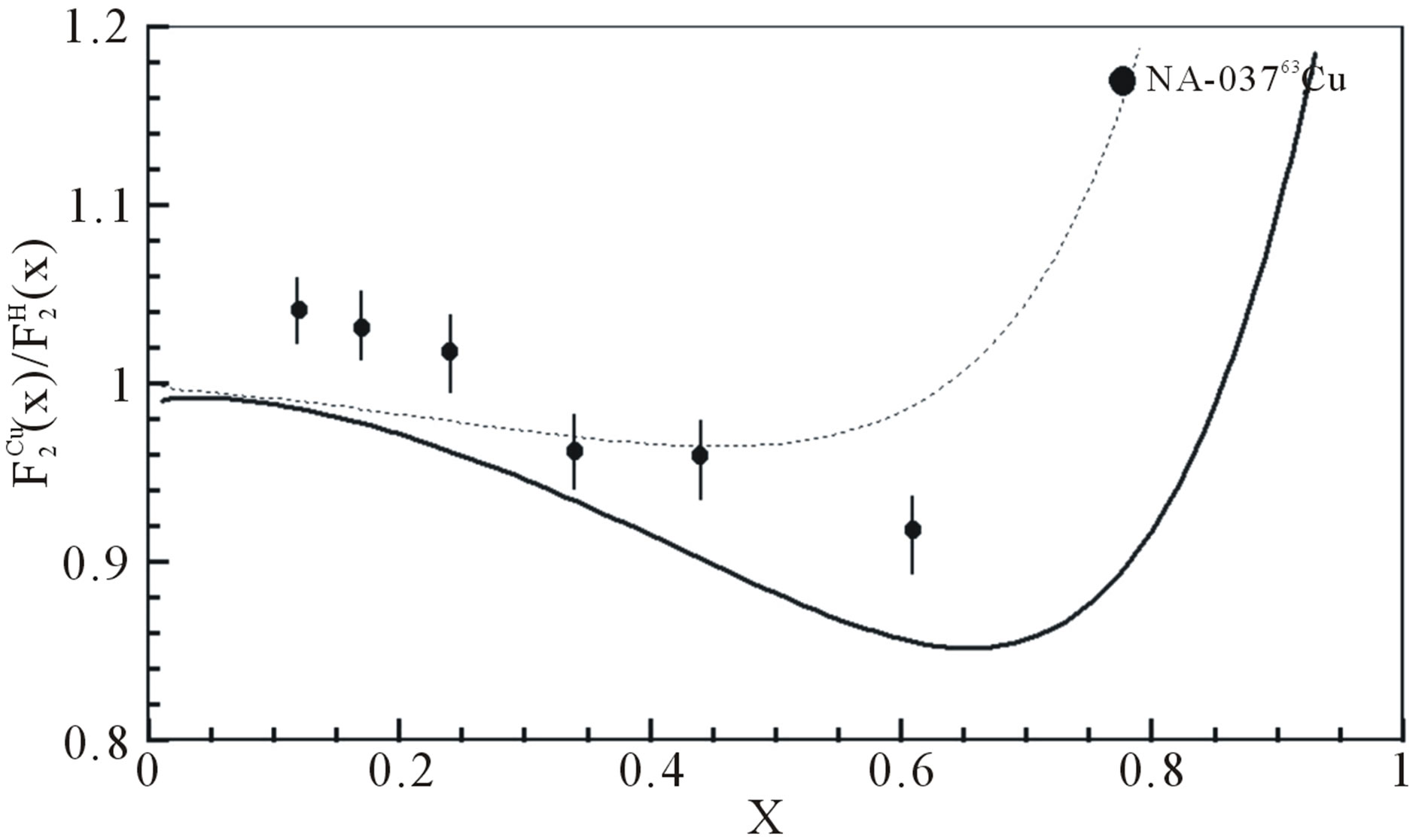
Figure 4. EMC ratios for, 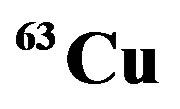 nucleus are plotted by using Equation (9), we used
nucleus are plotted by using Equation (9), we used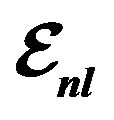 ,
, 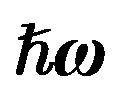 , and
, and 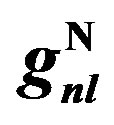 from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely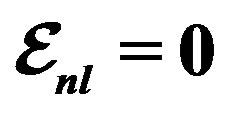 . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
where 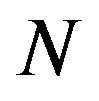 is number of neutron and
is number of neutron and  is the atomic number of nucleus A. The extracted results for
is the atomic number of nucleus A. The extracted results for  for
for ,
,  ,
, 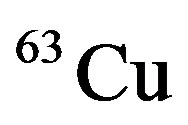 , and
, and 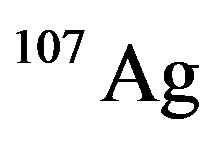 nuclei are plotted in Figures 6-9, respectively.
nuclei are plotted in Figures 6-9, respectively.
4. Results and Discussions
We plotted the EMC ratios in Figures 2-9. The extracted data has agreement with experimental data. This agreement have been obtained in the average binding energies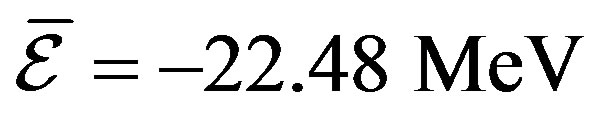 ,
,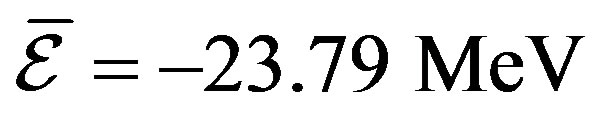 ,
, 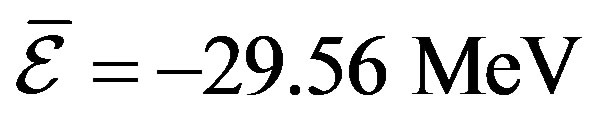 , and
, and 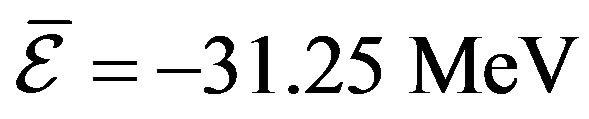 for
for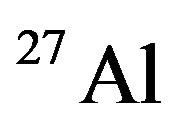 ,
, 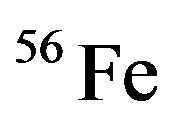 ,
, 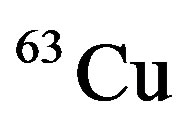 , and
, and 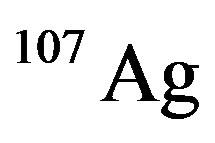 nuclei, respectively. We neglected other nuclear effects such as pion cloud [12,13], presence of Δ particle [14], quark exchange [15] and etc. Determining of Bind-
nuclei, respectively. We neglected other nuclear effects such as pion cloud [12,13], presence of Δ particle [14], quark exchange [15] and etc. Determining of Bind-
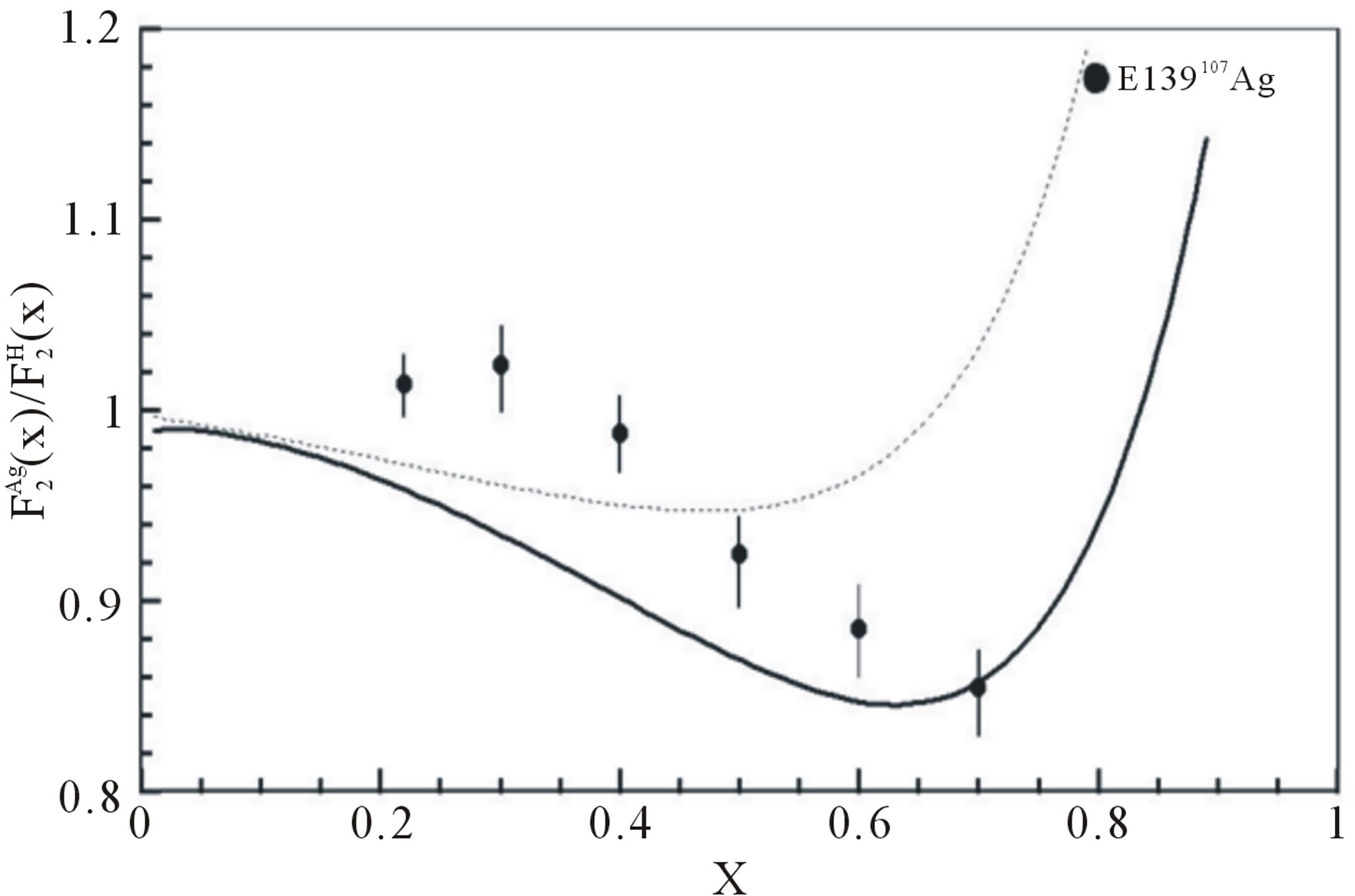
Figure 5. EMC ratios for, 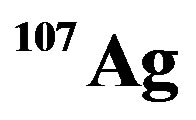 nucleus are plotted by using Equation (9), we used
nucleus are plotted by using Equation (9), we used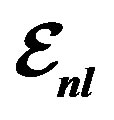 ,
, 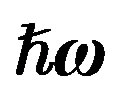 , and
, and  from Tables 1 and 2. Experimental data are taken from [10, 11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10, 11]. Dotted curve just shows Fermi motion effect, namely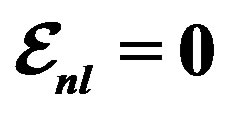 . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.

Figure 6. Structure function ratios are plotted according Equation (10) for 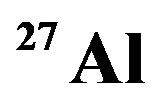 nucleus with considering Equation (2), we used
nucleus with considering Equation (2), we used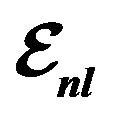 ,
, 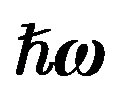 , and
, and 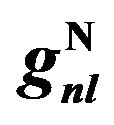 from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely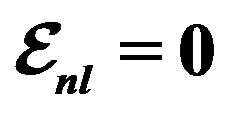 . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
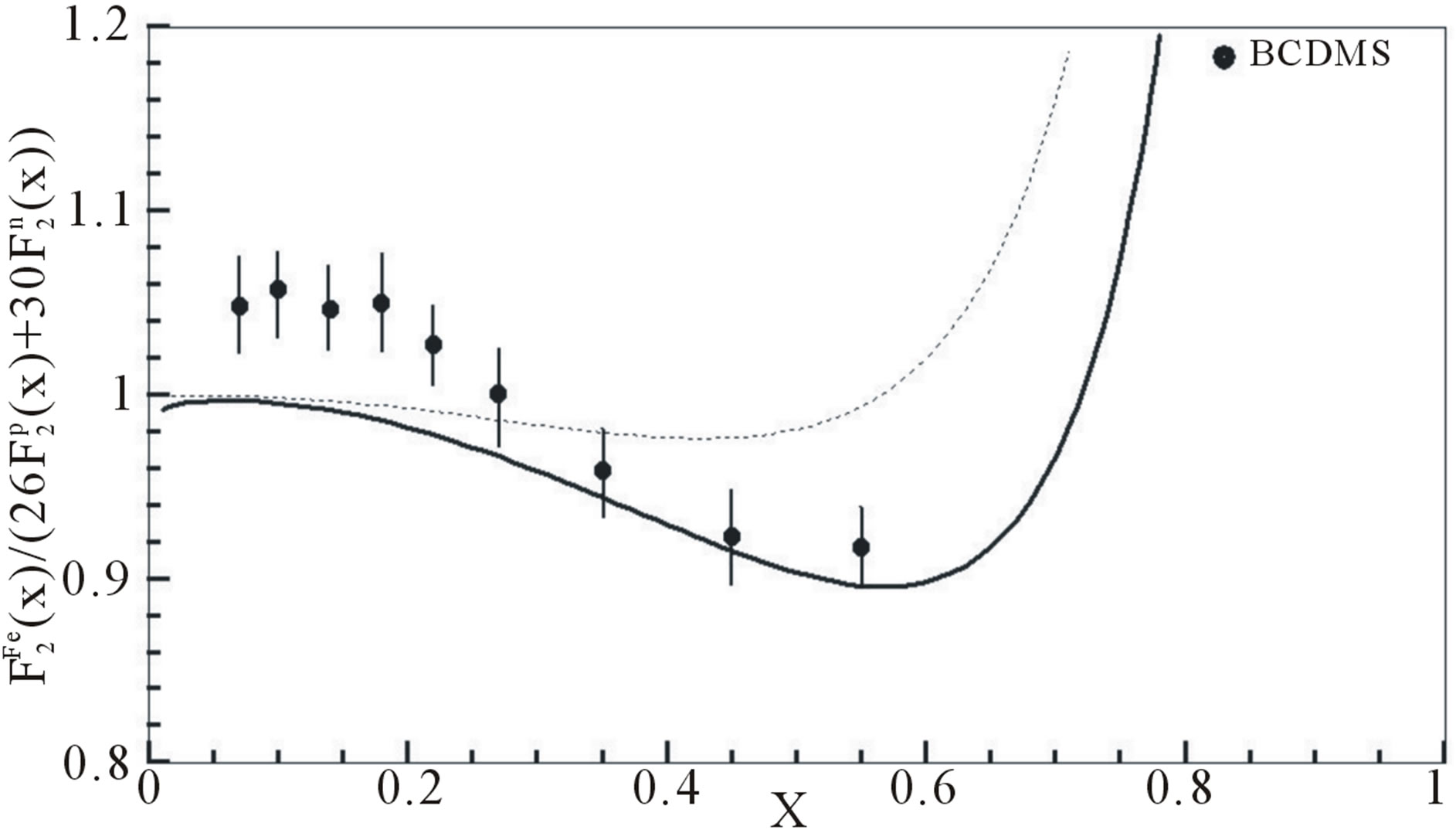
Figure 7. Structure function ratios are plotted according Equation (10) for  nucleus with considering Equation (2), we used
nucleus with considering Equation (2), we used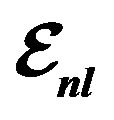 ,
, 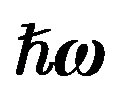 , and
, and 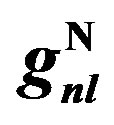 from Tables 1 and 2. Experimental data are taken from [10, 11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10, 11]. Dotted curve just shows Fermi motion effect, namely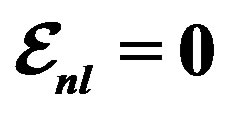 . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.

Figure 8. Structure function ratios are plotted according Equation (10) for,  nucleus with considering Equation (2), we used
nucleus with considering Equation (2), we used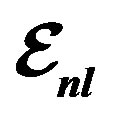 ,
, 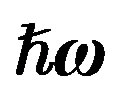 , and
, and 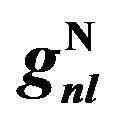 from Tables 1 and 2. Experimental data are taken from [10, 11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10, 11]. Dotted curve just shows Fermi motion effect, namely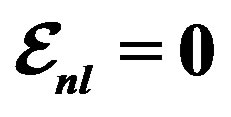 . The full curve shows both of the Fermi motion and the binding energy. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy. For used binding energy see Table 1.
ing energy 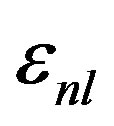 that is used in Equation (3) is an issue and the proposed average value for this parameter which could make agreement between extracted results from conventional nuclear theory and experimental data, is about –39 MeV for Iron [2,4]. But by considering some phenomena that caused by nuclear medium effect on structure functions this value could be decreased from –39 to –26 MeV [4]. In our assumption, we supposed in different shells, nucleons settled in different mean fields. Maybe this assumption causes some issue in conventional nuclear theory, but this could decrease average binding energy for example from –39 MeV to –23.79 MeV for Iron, without considering any other phenomena like flux factor or nuclear medium effects. These results show that in different shell if we suppose that nucleons
that is used in Equation (3) is an issue and the proposed average value for this parameter which could make agreement between extracted results from conventional nuclear theory and experimental data, is about –39 MeV for Iron [2,4]. But by considering some phenomena that caused by nuclear medium effect on structure functions this value could be decreased from –39 to –26 MeV [4]. In our assumption, we supposed in different shells, nucleons settled in different mean fields. Maybe this assumption causes some issue in conventional nuclear theory, but this could decrease average binding energy for example from –39 MeV to –23.79 MeV for Iron, without considering any other phenomena like flux factor or nuclear medium effects. These results show that in different shell if we suppose that nucleons

Figure 9. Structure function ratios are plotted according Equation (10) for 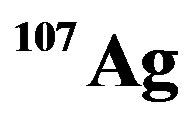 nucleus with considering Equation (2), we used
nucleus with considering Equation (2), we used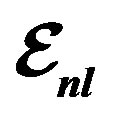 ,
, 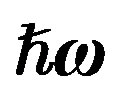 , and
, and 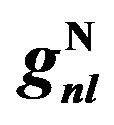 from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely
from Tables 1 and 2. Experimental data are taken from [10,11]. Dotted curve just shows Fermi motion effect, namely . The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
. The full curve shows both of the Fermi motion and the binding energy effects. For used binding energy see Table 1.
feel various mean fields, this assumption could get the EMC ratios that have agreement with experimental data in less binding energy. The binding energies and 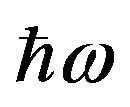 parameters that we used to get the EMC results for different shells could be found in Tables 1 and 2. If this calculation, in this framework, is utilized for heavy nuclei, we are expecting more compatibility between EMC ratios and shell model in conventional nuclear theory. In Figures 2-9, to extract full curve we used the binding energies in Table 1 for shells. The used energy for 2H is –1 MeV comparable with experimental binding energy per nucleon –1.1 MeV for deuterium.
parameters that we used to get the EMC results for different shells could be found in Tables 1 and 2. If this calculation, in this framework, is utilized for heavy nuclei, we are expecting more compatibility between EMC ratios and shell model in conventional nuclear theory. In Figures 2-9, to extract full curve we used the binding energies in Table 1 for shells. The used energy for 2H is –1 MeV comparable with experimental binding energy per nucleon –1.1 MeV for deuterium.
REFERENCES
- J. J. Aubert, G. Bassompierr, K. H. Becks, C. Best, E. Böhm, X. de Bouard, F. W. Brasse, et al., “The Ratio of the Nucleon Structure Functions F2N for Iron and Deuterium,” Physics Letters B, Vol. 123, No. 3-4, 1983, pp. 275-277. doi:10.1016/0370-2693(83)90437-9
- S. V. Akulinichev, S. Shlomo, S. A. Kulagin and G. M. Vagradov, “Lepton-Nucleus Deep-Inelastic Scattering,” Physical Review Letter, Vol. 55 No. 21, 1985, pp. 2239- 2241. doi:10.1103/PhysRevLett.55.2239
- G. V. Dunne and A. W. Thomas, “Deep Inelastic Scattering as a Probe of Nucleon and Nuclear Structure,” Nuclear Physics A, Vol. 446, No. 1-2, 1985, pp. 437-443. doi:10.1016/0375-9474(85)90617-7
- D. F. Geesaman, K. Saito and A. W. Thomas, “The Nuclear EMC Effect,” Annual Review Nuclear Particle Science, Vol. 45, No. 1, 1995, pp. 337-390. doi:10.1146/annurev.ns.45.120195.002005
- A. Preston and R. K. Bhaduri, “Structure of Nucleus,” Addison-Wesley Publishing Company, Boston, 1982.
- M. Gluck, E. Reya and A. Vogt, “Dynamical Parton Distributions of Parton and Small-x Physics,” Zeitschrift fur Physik C, Vol. 67, No. 3, 1995, pp. 433-447. doi:10.1007/BF01624586
- R. C. Barratt and D. F. Jackson, “Nuclear Sizes and Structure,” Oxford University Press, Oxford, 1977.
- F. Zolfagharpour, “EMC effect with different oscillatormodel parameters
 for different shells by considering difference between proton and neutron structure functions,” 2008. http://arxiv.org/abs/0802.1623v2
for different shells by considering difference between proton and neutron structure functions,” 2008. http://arxiv.org/abs/0802.1623v2 - http://durpdg.dur.ac.uk/
- J. Gomez, R. G. Arnold, P. E. Bosted, C. C. Chang, A. T. Katramatou, G. G. Petratos, et al., “Measurement of the A Dependence of Deep-Inelastic Electron Scattering,” Physical Review D, Vol. 49, No. 9, 1994, pp. 4348-4372. doi:10.1103/PhysRevD.49.4348
- B. L. Birbrair, M. G. Ryskin and V. I. Ryazanov, “Contribution of Boundness and Motion of Nucleus to the EMC Effect,” The European Physical Journal A, Vol. 25, No. 9, 2005, pp. 275-282. doi:10.1140/epja/i2005-10107-2
- T. Uchiyama and K. Saito, “European Muon Collaboration Effect in Deuteron and in Three-Body Nuclei,” Physical Review C, Vol. 38, No. 5, 1988, pp. 2245-2250. doi:10.1103/PhysRevC.38.2245
- E. L. Berger and F. Coester, “Nuclear Effects in DeepInelastic Lepton Scattering,” Physical Review D, Vol. 38, No. 5, 1985, pp. 1071-1083. doi:10.1103/PhysRevD.32.1071
- G. Cattapan and L. Ferreira, “The Role of the Δ in Nuclear Physics,” Physics Report, Vol. 362, No. 5-6, 2002, pp. 303-407. doi:10.1016/S0370-1573(01)00093-X
- P. Hoodbhoy and R. L. Jaffe, “Quark Exchange in Nuclei and the European Muon Collaboration Effect,” Physical Review D, Vol. 35, No. 1, 1987, pp. 113-121. doi:10.1103/PhysRevD.35.113
NOTES
*Corresponding author.

