Journal of Modern Physics
Vol.4 No.1(2013), Article ID:27256,6 pages DOI:10.4236/jmp.2013.41020
Nature of First-Order Transition in Planar Rotator Model with Modified Potential
1Institute of Physics, Bhubaneswar, India
2Department of Science and Technology, DST Project, New Delhi, India
Email: snehadri@hotmail.com
Received July 7, 2012; revised October 13, 2012; accepted October 31, 2012
Keywords: XY-Model; Spin Wave; Vortices
ABSTRACT
We have carried out micro-canonical Monte Carlo simulations of a planar rotator model in 30 × 30 lattice using periodic boundary conditions. The energy distribution of the rotator in the lattice shows features that can be associated with spin wave and vortex excitations. The results supplement the first-order transition observed in canonical Monte Carlo simulation, due to vortex nucleation. We also see features that can be associated with the in-homogeneity of vortex charge in the critical region.
1. Introduction
Simulations of statistical systems have gained much interest, recently [1-4]. The spin-models with continuous symmetry, such as the planar rotator model [5], has been studied significantly to know its properties and applicability to physical systems. In the past, effort has been made to know the type of phase transition in a magnetic material through planar rotator model [6]. It has also been used to study exotic materials such as high temperature superconductors [7] and super-fluids [8]. It is known that the planar rotator model shows several important properties: such as lack of long range order, the presence of topological defects called vortices, the vortex unbinding transition called Kosterlitz-Thouless (KT) transition, which is topological in nature [9-14]. The behavior of the system is known to be accurately described at sufficiently low temperatures by the “spin-wave” theories by Wegner [12] and Berezinskii [13] and later by Zittartz [14]. Various theoretical techniques have been used to study the spin waves and vortices [14,15]. Several canonical Monte Carlo (MC) simulations [16-22] have been carried out using the Metropolis procedure [23]. There are also studies with canonical MC simulations based on improved techniques [24-26] and the micro-canonical molecular dynamics algorithm [27]. Being of a topological nature, no specific heat anomaly is observed at the KT transition temperature TKT. But the temperature dependence of the specific heat shows a peak at a temperature, which is about 15% higher than TKT.
It has been found that the vortex unbinding transition temperature (Tv) increases by reducing the potential well width. On the other hand, local disorder sets in at temperatures near the potential well height
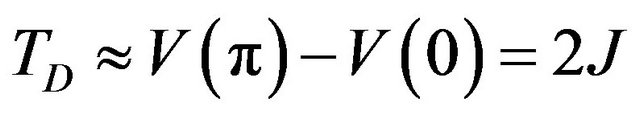 .
.
Therefore, for a sufficiently narrow potential well TD < Tv, we expect the continuous transition to yield to a first-order vacancy condensation transition. Several studies have been carried out to understand the first order transition in this system [28-48]. Here we report the study of the nature of the first order transition in a finite isolated system, which supplements the results observed in canonical Monte Carlo simulations [28,29].
The Hamiltonian of the planar rotator model with modified potential is given by:
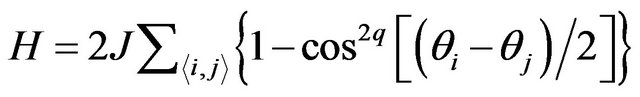 (1)
(1)
J in Equation 1 denotes the interaction strength (>0 for the ferromagnetic case) and the sum is over all the nearest neighbors [28]. In Equation (1), q = p2 is the controlling parameter and q > 0. As q is raised, it has an increasingly narrow well of width 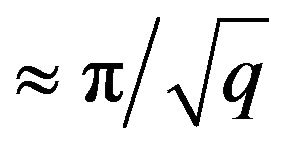 and for
and for 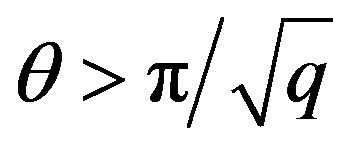 it is essentially constant at V(π) = 2J. For q = 1, the Hamiltonian gives rise to the Kosterlitz-Thouless transition and for large value of q, the transition is first-order in nature.
it is essentially constant at V(π) = 2J. For q = 1, the Hamiltonian gives rise to the Kosterlitz-Thouless transition and for large value of q, the transition is first-order in nature.
We performed micro-canonical Monte Carlo (MC) simulations [49,50] on 30 × 30 rotator system using the Hamiltonian given in Equation (1). There are also other simulation methods which have been reported recently [51,52]. We used periodic boundary conditions. It is known from renormalization group theory that fluctuations at all wave lengths are equally important around the phase transition [53]. For a 30 × 30 system, the boundary to area ratio is nearly 8 and therefore, one expects to see features of a large system. In the simulations there is an extra degree of freedom which exchanges energy with the rotator system. The temperature is directly related to the average energy of the extra degree of freedom :
:
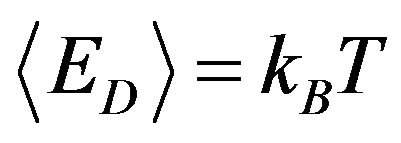 (2)
(2)
where kB is the Boltzmann constant. (Hereafter we replace kBT/J by T and E/J by E for simplicity). In these simulations the total energy (E) is an input parameter and the temperature (T) is determined from the simulations. The system was heated in steps across the first order transition during which energy was added to the rotator system through the demon. Figure 1 shows the energy as a function of temperature for q = 55. We used 5 × 105 Monte Carlo step per rotator (MCSR) for equilibration and 5 × 106 MCSR for averaging. We performed block averages consisting of 5 × 104 MCSR each and then found the standard deviation of the block averages. The standard deviation of the estimated temperature is less than about 0.5 percent. It is seen that the temperature dependence of energy shows a van der Waals-like loop at the first order transition, which occurs at T = 1.0. It is well known that meta-stability gives rise to van der Waals-like loop [54]. For instance; it arises in weaklong-range-force models. In the limit of infinite interaction range, the free-energy required towards a change to the equilibrium state is extensive and the mean-field approximation predicts that meta-stability lifetimes are infinite in the thermodynamic limit. We expect that such situation does not arise in the present study of finite systems. We note here that the canonical and the microcanonical ensembles are mathematically linked by the Laplace transform [55] and the micro-canonical results can be obtained from the canonical energy distribution Pβ,L(E) by the following equation [56]:
 (3)
(3)
We studied the system (was studied) for various energy values with 5 × 106 MCSR for equilibration and 5 × 106 MCSR for averaging. The standard deviation of the estimated temperature in this set, is also less than about 0.5 percent. We studied the energy distribution of a rotator in lattice after equilibration. Figures 2-4 show the energy distribution of the rotator in the lattice for various values of total system energy. In Figure 2 the values of E lies below that at the transition. It is seen that there is a broad peak after which the energy shows an exponential distribution.
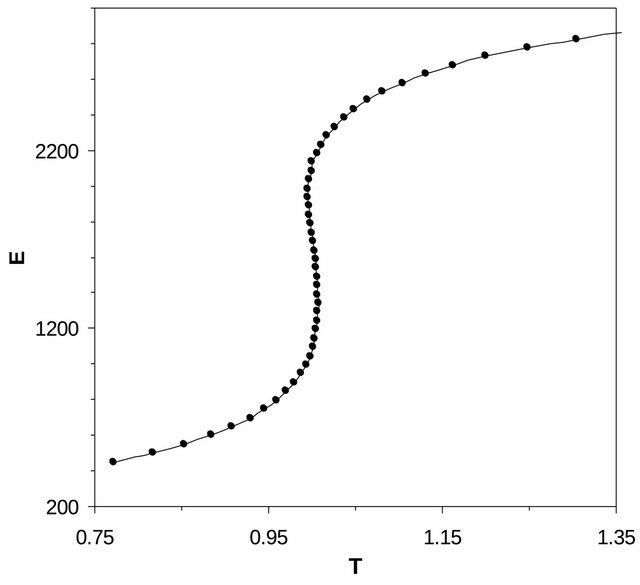
Figure 1. Temperature versus energy of the planar rotator model. The simulations are carried out on a 30 × 30 square lattice using periodic boundary conditions with q = 55. The van der Waals-like loop is observed at the first-order transition.

Figure 2. The frequency distribution of a rotator in the lattice for E = 400 (T = 0.717) (■) and E = 700 (T = 0.930) (○), which lie at low temperatures, below the first order transition: The ordinate represents the natural logarithm of the number of times out of the 5 × 106 MCSR that the rotator is in the corresponding energy bin of width 0.1.
We attribute this as due to the spin waves. In Figure 3 the values of E corresponds to that at the transition. It is seen that a peak at Es = 7.9 develops gradually apart from the broad low temperature peak which reduces in magnitude. There are also several intermediate peaks. In Figure 4, at high temperatures (above the transition), the broad low temperature peak is observed to be
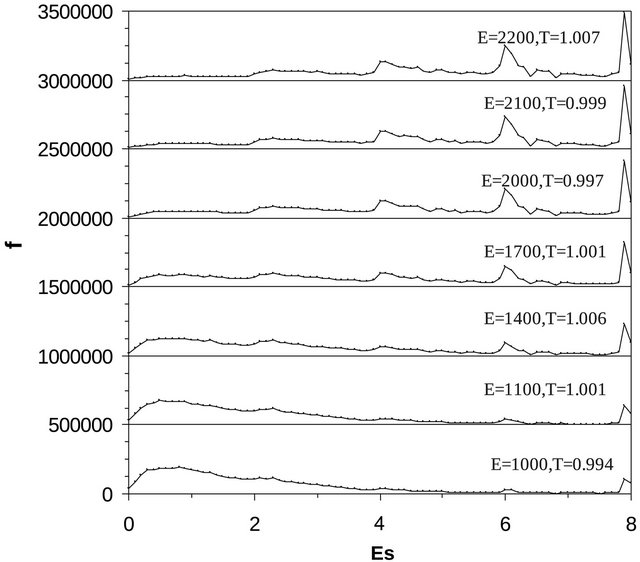
Figure 3. The frequency distribution of a rotator in the lattice for a range of system energies (temperatures) at the first order transition temperature: E = 1000 (T = 0.994) (lowest curve); 1100 (1.001); 1400 (1.006); 1700 (1.001); 2000 (0.997); 2100 (0.999); 2200 (1.007) (top most curve). The solid lines through the data are guide to the eye. The successive graphs are shifted along the ordinate by 5 × 105. The ordinate represents the number of times out of the 5 × 106 MCSR that the rotator is in the corresponding energy bin of width 0.1.
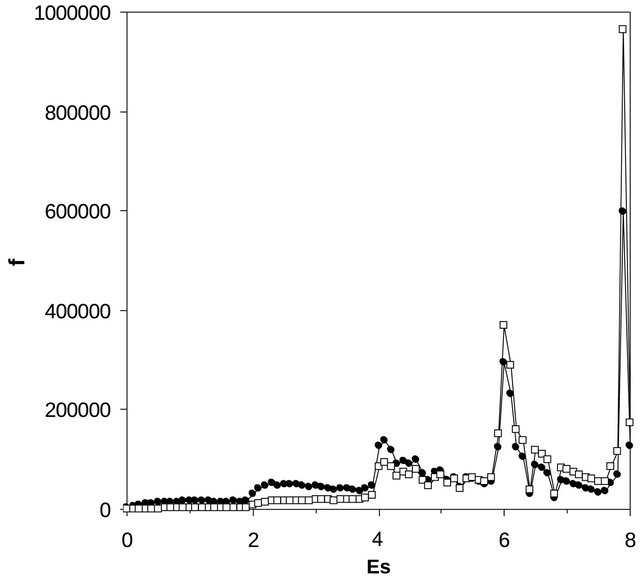
Figure 4. The frequency distribution of a rotator in the lattice for E = 2400 (T = 1.041) (●) and E = 2800 (T =1.273) (□), which lie at high temperatures, above the first order transition. The ordinate represents the number of times out of the 5 × 106 MCSR that the rotator is in the corresponding energy bin of width 0.1. The solid lines through the data are guide to the eye.
absent and the peak at Es = 7.9 continues to increase, along with the intermediate peaks. We attribute the high energy peak as due to the vortices. The height (or intensity) of the peaks which arises due to spin waves and vortices is shown as a function of system energy in Figure 5. It is seen that the peak due to the spin waves reduces as the energy increases and at the end of the transition this peak is practically absent. However, on the other hand, the peak due to the vortex excitations continue to increase above the first order transition.
It is known that, the spin waves dominate at low temperatures [12-14]. The broad peak at low temperatures (Figure 2), can be attributed as due to such excitation. The peak at Es = 7.9, is close to the value of energy needed to create a vortex-anti-vortex pair. The energy needed to create a vortex-anti-vortex pair (2μ) can be estimated from the expected exponential temperature dependence of vortex density: V~e–2μ/T [18]. We obtain a value of 2μ = 7.3 [57]. The low temperature value of 2μ corresponds to the energy associated with the closest bound vortex-anti-vortex pair. This can be compared with the vortex-anti-vortex pair in the absence of a spin wave with lowest energy configuration [42]. The corresponding energy is 8 in units of J. Recently, the vortices in the classical planar rotator have been studied using canonical MC simulations based on an improved technique. The value of 2μ = 7.55 obtained in the simulations are in good agreement with the present results [25]. We note here that the analytical value estimated by Kosterlitz and Thouless is 9.9. Therefore, this peak at Es = 7.9, can be attributed as due to vortices.
Simulations have shown that the vortex charge distribution is inhomogeneous [58]. The maximum in-homogeneity occurs at a temperature that corresponds to that of the coexistence region. Although we have not yet found an exact explanation of the observed in-homogeneity
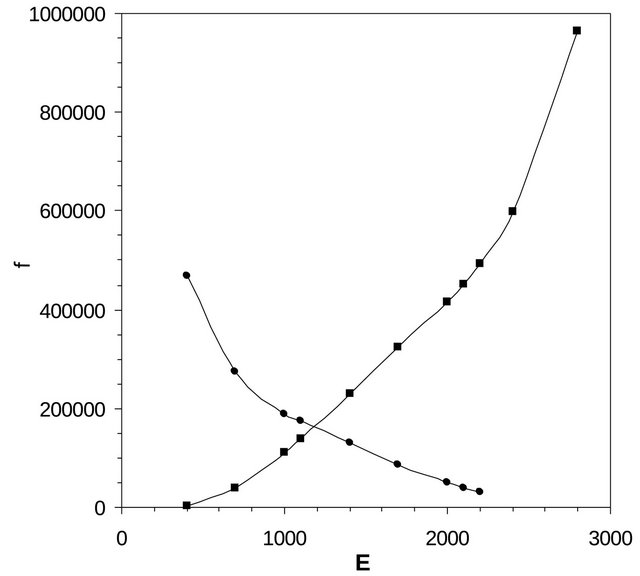
Figure 5. The intensities of the peak due to spin waves (●) and vortices (■) as a function of system energy. The solid lines through the data are guide to the eye.
of the vortices, certain features can be understood as follows. In the low temperature (energy) insulating phase the vortices are bound tightly which results in a small value of the vortex in-homogeneity. In the high temperature (energy) Debye-Hűckel regime, the in-homogeneity is also small due to the presence of a large number of free charges in the liquid phase. We speculate that cluster of vortices in the critical region are responsible for the peak in the vortex charge in-homogeneity. The intermediate peaks seen in Figures 3 and 4 can be attributed as due to the vortex-charge in-homogeneity.
In conclusion, we have studied the energy distribution of the rotator in the lattice. The energy distribution of the rotator, shows features that can be associated with spin wave and vortex excitations. The results substantiate the first-order transition observed in canonical Monte Carlo simulation, due to vortex nucleation. We also see features that can be associated with the in-homogeneity of vortex charge in the critical region.
2. Acknowledgements
The program for this simulation was developed at the Max-Planck-Institut für Festkörperforschung, Stuttgart, Germany. One of us (S. O.) acknowledges the financial support of the Department of Science and Technology, New Delhi.
REFERENCES
- J. Renn and D. Hoffmann, “1905—A Miraculus Year,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 38, No. 9, 2005, pp. S437-S448.
- O. G. Mouritsen, “Computer Studies of Phase Transitions and Critical Phenomena,” Springer, Berlin, 1984. doi:10.1007/978-3-642-69709-8
- K. Binder, “Theory of First-Order Phase Transitions,” Reports on Progress in Physics, Vol. 50, No. 7, 1987, pp. 783-859. doi:10.1088/0034-4885/50/7/001
- H. Gould and J. Tobochnik, “An Introduction to Computer Simulation Methods (Applications to Physical Systems, Part 2),” Addition-Wesley, New York, 1988.
- M. N. Barber, “Phase Transitions in Two Dimensions,” Physics Reports, Vol. 59, No. 4, 1980, pp. 375-409. doi:10.1016/0370-1573(80)90026-5
- L. J. de Jongh and A. R. Miedema, “Experiments on Simple Magnetic Model System,” Advances in Physics, Vol. 50, No. 8, 2001, pp. 947-1170. doi:10.1080/00018730110101412
- I. Morgenstern, K. A. Müller and J. G. Bednorz, “Numerical Simulations of a High-Tc Superconductive Glass Model,” Zeitschrift für Physik B Condensed Matter, Vol. 69, No. 1, 1987, pp. 33-47. doi:10.1007/BF01560607
- N. Goldenfeld, “Lectures on Phase Transition and Renormalization Group,” Addison-Wesley, Reading, 1992.
- N. D. Mermin and H. Wagner, “Absence of Ferromagnetism or Antiferromagnetism in Oneor Two-Dimensional Isotropic Heisenberg Models,” Physical Review Letters, Vol. 17, No. 22, 1966, pp. 1133-1136. doi:10.1103/PhysRevLett.17.1133
- V. L. Berezinskii, “Destruction of Long Range Order in One Dimensional and Two Dimensional Systems Having a Continuous Symmetry Group I. Classical Systems,” Soviet Physics JETP, Vol. 32, 1971, pp. 493-500.
- J. M. Kosterlitz and D. J. Thouless, “Long Range Order and Metastability in Two Dimensional Solids and Superfluids. (Application of Dislocation Theory),” Journal of Physics C: Solid State Physics, Vol. 7, No. 6, 1974, p. 1046. doi:10.1088/0022-3719/7/6/005
- F. J. Wegner, “Spin-Ordering in a Planar Classical Heisenberg Model,” Zeitschrift für Physik, Vol. 206, No. 5, 1967, pp. 465-470. doi:10.1007/BF01325702
- V. L. Berezinskii, Soviet Physics JETP, Vol. 34, 1971, p. 610.
- J. Zittartz, “Phase Transition of the Two-Dimensional Classical XY-Model,” Zeitschrift fur Physik B, Vol. 23, No. 1, 1976, pp. 55-69.
- J. V. Jose, L. P. Kadanoff, S. Kirkpatrick and D. J. Nelson, “Renormalization, Vortices and Symmetry-Breaking Perturbations in the Two-Dimensional Planar Model,” Physical Review B, Vol. 16, No. 3, 1977, pp. 1217-1241. doi:10.1103/PhysRevB.16.1217
- C. Kawabata and K. Binder, “Evidence for Vortex Formation in Monte Carlo Studies of the Two-Dimensional XY-Model,” Solid State Communications, Vol. 22, No. 11, 1977, pp. 705-710. doi:10.1016/0038-1098(77)90255-1
- S. Miyashita, H. Nishimori, A. Kuroda and M. Suzuki, “Monte Carlo Simulation and Static and Dynamic Critical Behavior of the Plane Rotator Model,” Progress of Theoretical Physics, Vol. 60, No. 6, 1978, 1669-1685. doi:10.1143/PTP.60.1669
- J. Tobochnik and G. V. Chester, “Monte Carlo Study of the Planar Spin Model,” Physical Review B, Vol. 20, No. 9, 1979, pp. 3761-3769. doi:10.1103/PhysRevB.20.3761
- W. J. Shugard, J. D. Weeks and G. H. Gilmer, “MonteCarlo Simulation of the Planar Model Using the Dual Solid-on-Solid Representation,” Vol. 21, No. 11, 1980, pp. 5309-5311. doi:10.1103/PhysRevB.21.5309
- J. E. van Himbergen and S. Chakravarty, “Helicity Modulus and Specific Heat of Classical XY Model in Two Dimensions,” Physical Review B, Vol. 23, No. 1, 1984, pp. 359-361. doi:10.1103/PhysRevB.23.359
- H. Betsuyaku, “Monte Carlo Renormalization of Kadanoff Block Transformation in the 2-d Plane-Rotator Model,” Physica A, Vol. 106, No. 1, 1981, pp. 311-325. doi:10.1016/0378-4371(81)90229-6
- J. F. Fernandes, M. F. Ferreira and J. Stankiewicz, “Critical Behavior of the Two Dimensional XY Model: A Monte Carlo Simulation,” Physical Review B, Vol. 34, No. 1, 1986, pp. 292-300. doi:10.1103/PhysRevB.34.292
- N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller and E. Teller, Journal of Chemical Physics, Vol. 21, 1953, p. 1087.
- R. Gupta, J. Delapp, G. G. Batrouni, G. C. Fox, C. F. Baillie and J. Apostolakis, “Phase Transition in the 2D XY Model,” Physical Review Letters, Vol. 61, No. 17, 1988, pp. 1996-1999. doi:10.1103/PhysRevLett.61.1996
- R. Gupta and C. F. Baillie, “Critical Behavior of the Two-Dimensional XY Model,” Physical Review B, Vol. 45, No. 6, 1992, pp. 2883-2898. doi:10.1103/PhysRevB.45.2883
- U. Wolff, “Collective Monte Carlo Updating in a High Precision Study of X-Y Model,” Nuclear Physics B, Vol. 322, No. 3, 1989, pp. 759-774. doi:10.1016/0550-3213(89)90236-8
- J. Kogut and J. Polonyi, “Microcanonical Study of the Planar Spin Model,” Nuclear Physics B, Vol. 265, 1986, pp. 313-323. doi:10.1016/0550-3213(86)90312-3
- E. Domany, M. Schick, R. H. Swendsen, “First-Order Transition in an xy Model with Nearest-Neighbor Interactions,” Physical Review Letters, Vol. 52, No. 17, 1984, pp. 1535-1538. doi:10.1103/PhysRevLett.52.1535
- J. E. van Himbergen, “From Continuous to First-Order Transition in a Simple XY Model,” Physical Review Letters, Vol. 53, No. 1, 1984, pp. 5-8. doi:10.1103/PhysRevB.29.6387
- J. E. Hirsh, “Charge-Density-Wave to Spin-Density-Wave Transition in the Extended Hubbard Model,” Physical Review Letters, Vol. 53, No. 24, 1984, pp. 2327-2330. doi:10.1103/PhysRevLett.53.2327
- H. J. F. Knops, “First-Order Transition in the XY Model,” Physical Review B, Vol. 30, No. 1, 1984, pp. 470- 472. doi:10.1103/PhysRevB.30.470
- J. E. van Himbergen, “Kosterlitz-Thouless Transitions in Simple Spin Models with Strongly Varying Vortex Densities,” Solid State Communications, Vol. 55, No. 4, 1985, pp. 289-193. doi:10.1016/0038-1098(85)90610-6
- D. Frenkel and R. Eppenga, “Evidence for Algebraic Orientational Order in a Two-Dimensional Hard-Core Nematic,” Physical Review A, Vol. 31, No. 3, 1985, pp. 1776-1787. doi:10.1103/PhysRevA.31.1776
- K. J. Strandburg, “Two-Dimensional Melting,” Reviews of Modern Physics, Vol. 60, No. 1, 1988, pp. 161-207. doi:10.1103/RevModPhys.60.161
- J. R. Lee and S. Teitel, “New Critical Behavior in the Dense Two-Dimensional Classical Coulomb Gas,” Physical Review Letters, Vol. 64, No. 13, 1990, pp. 1483- 1486. doi:10.1103/PhysRevLett.64.1483
- M. J. P. Gingras, P. C. W. Holdsworth and B. Bergersen, “Monte Carlo Study of Induced Bond Orientational Ordering in Two-Dimensional Liquid-Crystal Models,” Physical Review A, Vol. 41, No. 12, 1990, pp. 6786-6795. doi:10.1103/PhysRevA.41.6786
- T. Garel, J. C. Niel and H. Orland, “Disorder Lines and Nonmonotonous Renormalization Group Flows: Application to the Two-Dimensional XY-Model,” Europhysics Letters, Vol. 11, No. 4, 1990, pp. 349-354. doi:10.1209/0295-5075/11/4/010
- P. Olsson and P. Minnhagen, “Interplay between Oneand Two-Dimensional Fluctuations for a Class of XY Models,” Physical Review B, Vol. 43, No. 4, 1991, pp. 3356-3361. doi:10.1103/PhysRevB.43.3356
- S. E. Korshunov, “Disorder Induced First-Order Transition in Superconducting Flims,” Physical Review B, Vol. 46, No. 10, 1992, pp. 6615-6617. doi:10.1103/PhysRevB.46.6615
- A. Jonsson, P. Minnhagen and M. Nylén, “New Critical Point for Two Dimensional XY-Type Models,” Physical Review Letters, Vol. 70, No. 9, 1993, pp. 1327-1330. doi:10.1103/PhysRevLett.70.1327
- G. M. Zhang, H. Chen and X. Wu, “First-Order Transition in the Dense Two-Dimensional Classical Coulomb Gas,” Physical Review B, Vol. 48, No. 16, 1993, pp. 12304- 12307. doi:10.1103/PhysRevB.48.12304
- F. Mila, “First-Order versus Kosterlitz-Thouless Transition in a Class of Modified XY-Model,” Physical Review B, Vol. 47, No. 1, 1993, pp. 442-445. doi:10.1103/PhysR evB.47.442
- C. Timm, “Flux Noise in High-Temperature Superconductors,” Physical Review B, Vol. 55, No. 5, 1997, pp. 3241-3248. doi:10.1103/PhysRevB.55.3241
- A. Jonsson and P. Minnhagen, “Complex Impedance of a Two-Dimensional Josephson Junction Array,” Physica C, Vol. 277, No. 3-4, 1997, pp. 161-169. doi:10.1016/S0921-4534(97)00098-1
- A. Jonsson and P. Minhagen, “Characteristics of TwoDimensional Vortex Dynamics from XY-Type Models with Ginzburg-Landau Dynamics,” Physical Review B, Vol. 55, No. 14, 1997, pp. 9035-9046. doi:10.1103/PhysRevB.55.9035
- Ch. Dellago and H. A. Posch, “Lyapunov Instability in the Extended XY-Model: Equilibrium and Non Equilibrium Molecular Dynamics Simulations,” Physica A, Vol. 237, No. 1, 1997, pp. 95-112. doi:10.1016/S0378-4371(96)00423-2
- G. Alvarez and H. Fort, “On the Nature of the Phase Transition Triggered by Vortex-Like Defects in the 2D Ginzburg-Landau Model,” Physics Letters A, Vol. 282, No. 6, 2001, pp. 399-406. doi:10.1016/S0375-9601(01)00210-9
- K. Medvedyeva, B. J. Kim and P. Minnhagen, “Ubiquitous Finite-Size Scaling Features in I-V Characteristics of Various Dynamic XY Models in Two Dimensions,” Physica C, Vol. 355, No. 1-2, 2001, pp. 6-14. doi:10.1016/S0921-4534(01)00026-0
- M. Creutz, “Microcanonical Monte Carlo Simulation,” Physical Review Letters, Vol. 50, No. 19, 1983, pp. 1411- 1414. doi:10.1103/PhysRevLett.50.1411
- S. Ota, S. B. Ota and M. Fähnle, “Microcanonical Monte Carlo Simulation for the Two-Dimensional XY Model,” Journal of Physics: Condensed Matter, Vol. 4, No. 24, 1992, pp. 5411-5418. doi:10.1088/0953-8984/4/24/011
- D. P. Landau, S. H. Tsai and M. Exler, “A New Approach to Monte Carlo Simulations in Statistical Physics: WangLandau Sampling,” American Journal of Physics, Vol. 72, No. 10, 2004, pp. 1294-1302. doi:10.1119/1.1707017
- O. Hammrich, “New Multiple Histogram Method for Studying Phase Transition,” Zeitschrift fur Physik B, Vol. 92, No. 4, 1993, pp. 501-505. doi:10.1007/BF01320513
- K. G. Wilson and J. Kogut, “The Renormalization Group and the e Expansion,” Physics Reports, Vol. 12, No. 2, 1974, pp. 75-200. doi:10.1016/0370-1573(74)90023-4
- P. A. Rikvold and B. M. Gorman, In: D. Stauffer, Ed., Annual Reviews of Computational Physics I, World Scientific, Singapore City, 1994.
- D. H. E. Gross, “Microcanonical Thermodynamics and Statistical Fragmentation of Dissipative Systems,” Physics Reports, Vol. 279, No. 3, 1997, pp. 119-201. doi:10.1016/S0370-1573(96)00024-5
- W. Janke, “Canonical versus Microcanonical Analysis of First-Order Phase Transitions,” Nuclear Physics B, Vol. 63, No. 1-3, 1998, pp. 631-633.
- S. B. Ota and S. Ota, “Vortices in the 2d Classical XYModel: A Microcanonical Monte Carlo Simulation Study,” Physics Letters A, Vol. 206, No. 1-2, 1995, pp. 133- 136. doi:10.1016/0375-9601(95)00588-T
- S. B. Ota and S. Ota, “Inhomogeneity of Vortex Charge in the 2D Classical XY Model,” Physics Letters A, Vol. 241, No. 1, 1998, pp. 127-130. doi:10.1016/S0375-9601(98)00034-6

