Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22622,4 pages DOI:10.4236/jmp.2012.39135
All the Fundamental Massless Fermion Fields in Superstring Theory: A Rigorous Analysis
The Institute for Fundamental Study, Naresuan University, Phitsanulok, Thailand
Email: manoukian_eb@hotmail.com
Received July 2, 2012; revised August 6, 2012; accepted August 14, 2012
Keywords: Massless Fermion Fields in Superstring Theory; Rarita-Schwinger Field (the Gravitino) in 10 Dimensions; Propagator Theory
ABSTRACT
A systematic rigorous analysis of both massless fermion fields in the mass spectra of superstring theory is carried out. Our interest is in dynamical aspects of these fields. An explicit novel expression for the propagator of the massless Rarita-Schwinger field (the gravitino), in the mass spectrum involving massless fermions in superstring theory in 10 dimensions, is derived. The analysis is carried in the presence of a non-constrained external source so that the full expression of the propagator emerges. The number of associated degrees of freedom is also obtained. We work in a Coulomb-like gauge. The massless Dirac field (the dilatino), the other massless fermion field in the mass spectra of superstring theory in 10 dimensions, is first investigated to this end.
1. Introduction
This work is involved with a systematic rigorous analysis of all the massless fermion fields in superstring theory. The two massless fermion fields arising in the mass spectrum in superstring theory are the Dirac (the dilatino) and the Rarita-Schwinger (the gravitino) fields in 10 dimensions (cf. [1,2]). What is remarkable about string theory is that the fundamental fields that are required to describe the dynamics of elementary particles arise naturally in the mass spectra of oscillating springs and are not, a priori, assumed to exist or put in by hand in the underlying theories. At present only the massless fields string modes are really physically relevant because of the enormous masses of the massive fields string-excitation modes. In this paper, we are interested in both massless fermionic field excitations in superstring theory. We are interested, particularly, in dynamical aspects of the gravitino field which is the main challenge here. To this end, we are concerned about the underlying constraints, the explicit expressions of its propagator, its inherit degrees of freedom. We work in the celebrated Coulomb gauge. For a systematic analysis of all the massless bosonic fields in superstring theory see [3] (also [4]). The fermionic massless fields, however, require some special techniques spelled out here. The Rarita-Schwinger field is necessarily coupled to a non-constrained external source so that the full expression of the propagator is obtained leading to a novel expression for it. The Dirac field is also necessarily considered first as a preparation for the investigation of the intricacies of the Rarita-Schwinger field from the dynamical aspects mentioned above. The Greek indices  go over 0, 1, ···, 9, while the Latin ones,
go over 0, 1, ···, 9, while the Latin ones, 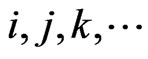 go over 1, 2, ···, 9. Summation over repeated indices is understood.
go over 1, 2, ···, 9. Summation over repeated indices is understood.
2. The Dirac Field in Ten Dimensions
To carry out the analysis involving the massless RaritaSchwinger field in ten dimensions, it is necessary first to review briefly and introduce, in the process, the following 8 gamma matrices:
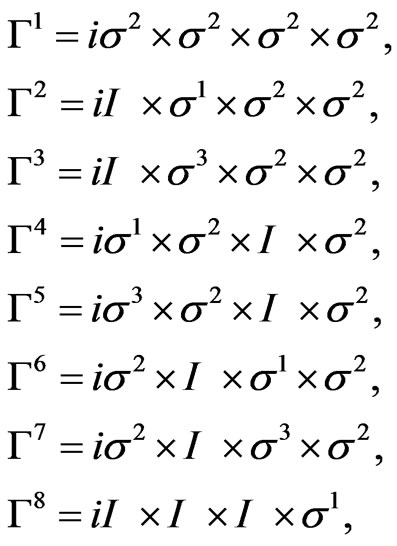 (1)
(1)
which are anti-commuting in pairs, and, in turn, introduce the product
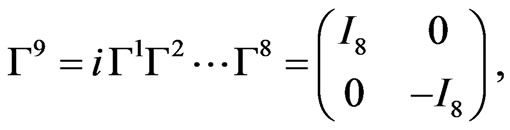 (2)
(2)
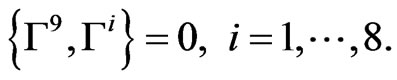 (3)
(3)
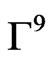 has the structure
has the structure
 (4)
(4)
All of the 16 by 16 matrices  are pure imaginary and satisfy the conditions:
are pure imaginary and satisfy the conditions:
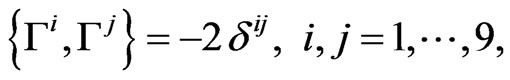 (5)
(5)
 (6)
(6)
A simple way to derive the Dirac equation in ten dimensions, is to multiply the equation:
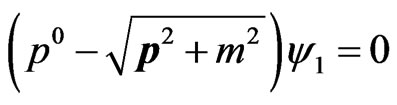 by
by 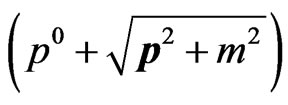 to obtain
to obtain
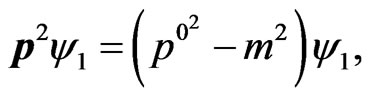 (7)
(7)
where p is 9 dimensional. Equation (7) may be re-written as
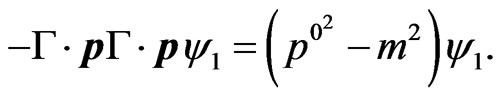 (8)
(8)
Simply call the combination 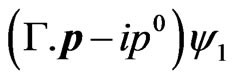 to be
to be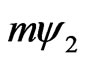 , i.e., define
, i.e., define
 (9)
(9)
Upon multiplying the latter by 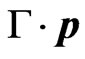 and using (7), (8), and (9) again, lead simply to
and using (7), (8), and (9) again, lead simply to
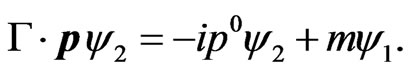 (10)
(10)
The two Equations (9) and (10), may be now readily combined into the elegant form
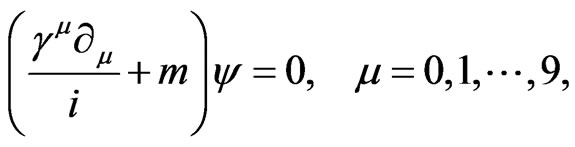 (11)
(11)
 (12)
(12)
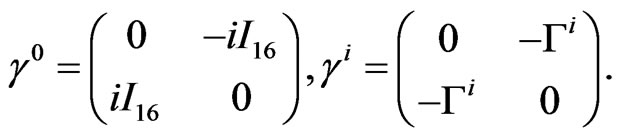 (13)
(13)
Thus we have an explicit representation of all the gamma matrices in 10 dimensions. They are all pure imaginary, and satisfy
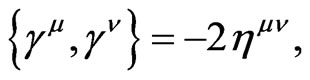 (14)
(14)
where
 (15)
(15)
Using, in the process, Equation (13), one may define the chirality matrix by
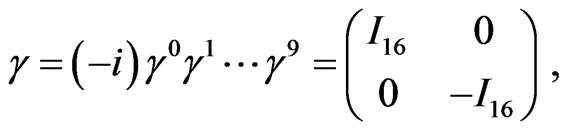 (16)
(16)
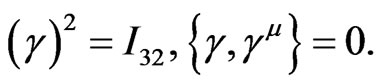 (17)
(17)
For 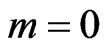 the two equations in (9), (10) decouple. From the expression of
the two equations in (9), (10) decouple. From the expression of  in (16), we may select a spinor with a definite chirality, say one with positive chirality
in (16), we may select a spinor with a definite chirality, say one with positive chirality
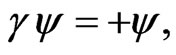 (18)
(18)
referred to as a Weyl spinor of positive chirality. From the structure of  in (12), this amounts in selecting
in (12), this amounts in selecting 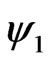 which, from (9), satisfies the equation
which, from (9), satisfies the equation 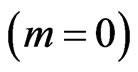
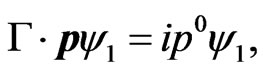 (19)
(19)
where 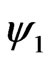 has 16 components, and this equation projects out further half of the components, leaving 8 independent components.
has 16 components, and this equation projects out further half of the components, leaving 8 independent components.
3. The Rarita-Schwinger Field in Ten Dimensions
The Lagrangian density for the Rarita-Schwinger field for  is given by (cf. [5,6])
is given by (cf. [5,6])
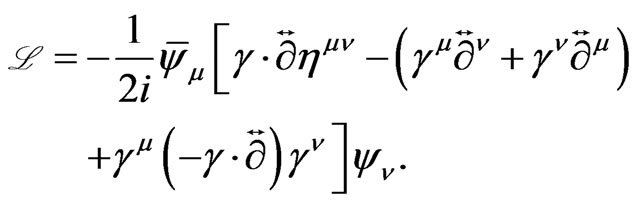 (20)
(20)
The Lagrangian density is, up to a total derivative, invariant under a gauge transformation 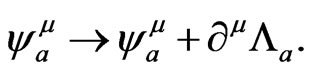
We work in a Coulomb-like gauge
 (21)
(21)
summing over i from 1 to 9. Now we add external sources to the Lagrangian density in (20) obtaining
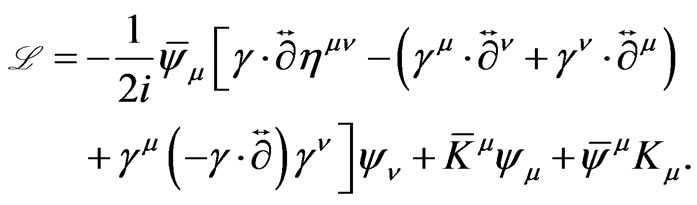 (22)
(22)
Due to the constraint in (21), the field components may not be varied independently. We may, however, express the field in terms of fields 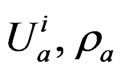 that may be varied independently as follows:
that may be varied independently as follows:
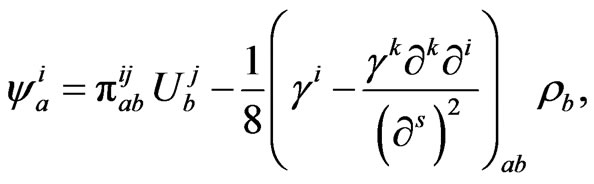 (23)
(23)
where
 (24)
(24)
satisfying
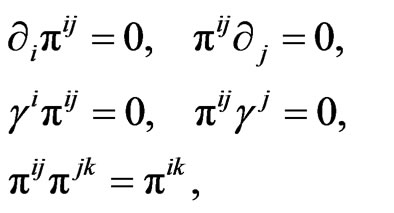 (25)
(25)
![]() and
and  is a projection operator, with
is a projection operator, with 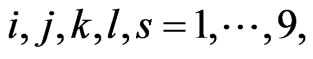 and a summation over repeated indices is understood.
and a summation over repeated indices is understood.
With 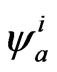 given in (23), we may now vary the fields
given in (23), we may now vary the fields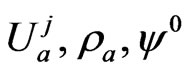 , which, as seen below, not only lead to the field equations but to additional (derived) constraints.
, which, as seen below, not only lead to the field equations but to additional (derived) constraints.
To the above end, we note, in particular, that we may write
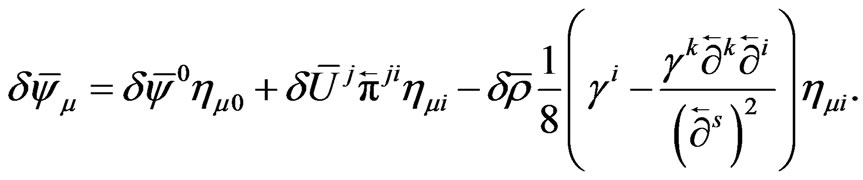 (26)
(26)
Using the above expression and by varying the Lagrangian density with respect to 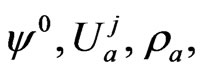 lead after some labor, to the equations
lead after some labor, to the equations
 (27)
(27)
 (28)
(28)
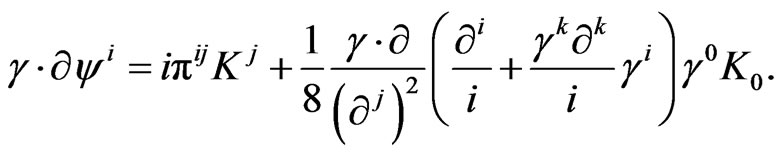 (29)
(29)
From these equations, we note that only  may propagate. Also if constraints are, a priori, imposed on
may propagate. Also if constraints are, a priori, imposed on , the right-hand sides of these equations are changed and the equations would not provide the full expression of the propagator.
, the right-hand sides of these equations are changed and the equations would not provide the full expression of the propagator.
We see from Equation (29), that the Coulomb-like condition in (21) is automatically satisfied. In the absence of the external sources, the above other two equations give also the constraints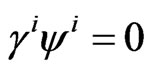 , and
, and 
That is, for a given spinor index, the number of states is reduced from a factor of 10 to 7. This is rigorously established by explicitly evaluating the contraction of 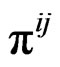 in (24):
in (24):
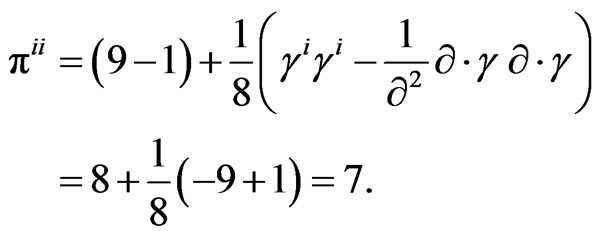 (30)
(30)
Hence from (19), for a given chirality, the number of total independent components would be 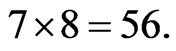
Since no constraints were imposed on the external sources 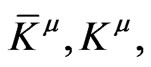 we may vary each of their components independently, otherwise the full expression of the propagator does not follow from the right-hand sides of (28), (29). Upon taking the vacuum expectation values
we may vary each of their components independently, otherwise the full expression of the propagator does not follow from the right-hand sides of (28), (29). Upon taking the vacuum expectation values 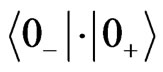 of (28), (29), and setting
of (28), (29), and setting
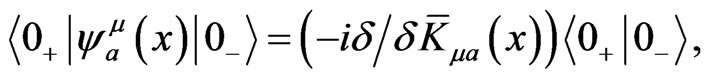
and integrating with respect to the sources, we obtain
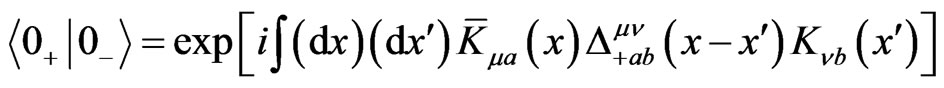 , (31)
, (31)
where the propagator 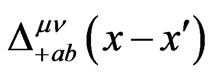 is given by
is given by
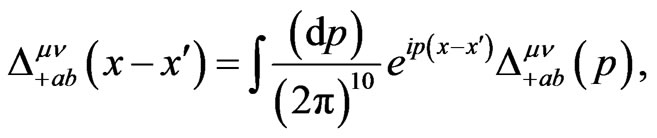 (32)
(32)
and 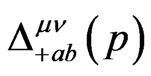 is explicitly worked out to be
is explicitly worked out to be
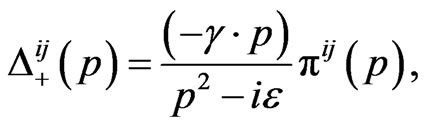 (33)
(33)
 (34)
(34)
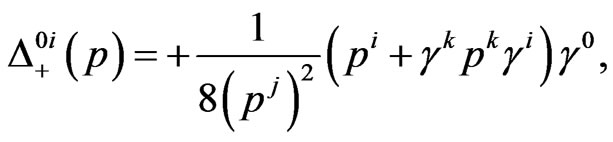 (35)
(35)
 (36)
(36)
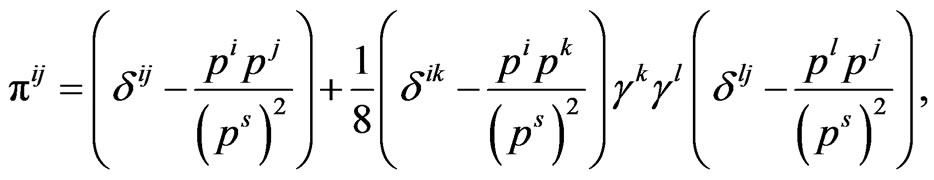 (37)
(37)
as the novel expressions of the components of the propagator.
4. Conclusion
A systematic rigorous analysis of both massless fermion fields in superstring theory in 10 dimensions was developed, emphasizing dynamical aspects, the constraints and the inherit non-trivial number of independent degrees of freedom, and a novel expression for the propagator of the Rarita-Schwinger was derived. For the treatment of all the massless bosonic fields of superstring theory see [3,4]. The investigations of the dynamical aspects of all these fields in superstring theory, are expected to be useful in finding connections between string theory and field theory for computations and for the generation of non-trivial effective actions. These points will be taken up in subsequent reports.
5. Acknowledgements
The author would like to thank his colleagues at the Institute for Fundamental Study of Naresuan University for the interest they have shown in this work and for their support. The author would like also to thank Professor T. Vijaktanawudhi for converting the manuscript from Latex to MS-word, and Professor N. Yongram for additional details to this end.
REFERENCES
- M. B. Green, J. H. Schwarz and E. Witten, “Superstring Theory, Vols.1 and 2,” Cambridge University Press, Cambridge, 1988.
- K. Becker, M. Becker and J. H. Schwarz, “String Theory and M-Theory,” Cambridge University Press, Cambridge, 2007.
- E. B. Manoukian, “All the Fundamental Massless Bosonic Fields in Superstring Theory,” Fortschritte der Physik, Vol. 60, No. 4, 2012, pp. 337-344. doi:10.1002/prop.201200043
- E. B. Manoukian, “All the Fundamental Massless Bosonic Fields in Bosonic String Theory,” Fortschritte der Physik, Vol. 60, No. 4, 2012, pp. 329-336. doi:10.1002/prop.201200003
- W. Rarita and J. Schwinger, “On a Theory of Particles with Half-Integral Spin,” Physical Review, Vol. 60, No. 1, 1941, p. 61. doi:10.1103/PhysRev.60.61
- J. Schwinger, “Particles, Sources and Fields, Vol. I,” Addison-Wesley, Boston, 1970.

