Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21690,6 pages DOI:10.4236/jmp.2012.38106
On Self-Similarity of Top Production at Tevatron
1Joint Institute for Nuclear Research, Moscow, Russia
2Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Prague, Czech Republic
Email: *tokarev@jinr.ru
Received June 7, 2012; revised July 1, 2012; accepted July 31, 2012
Keywords: Inelastic Cross Section; Proton-antiProton Collisions; Top Production; Scaling; Self-Similarity
ABSTRACT
This paper presents the results of analysis of the DØ 1.0 fb–1 data on top-quark differential cross section measurements at the Fermilab Tevatron collider at 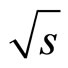 = 1960 GeV in the framework of z-scaling approach. The flavor independence of scaling function
= 1960 GeV in the framework of z-scaling approach. The flavor independence of scaling function 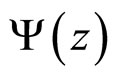 observed in pp and
observed in pp and  interactions over a wide collision energy range
interactions over a wide collision energy range 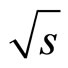 = 19 - 1960 GeV has been verified. This property of
= 19 - 1960 GeV has been verified. This property of 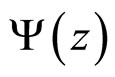 was found for different hadrons—from π-mesons up to Υ particles. The flavor independence of
was found for different hadrons—from π-mesons up to Υ particles. The flavor independence of  is used as indication on self-similarity of the top-quark production. A tendency to saturation of
is used as indication on self-similarity of the top-quark production. A tendency to saturation of  at low z for top-quark production has been confirmed. Momentum fraction x1 of the incoming (anti)protons as a function of the scaled transverse momentum
at low z for top-quark production has been confirmed. Momentum fraction x1 of the incoming (anti)protons as a function of the scaled transverse momentum 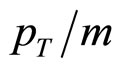 and masses of heavy mesons is studied. We anticipate that the data on lowand high-pT inclusive spectra of the top-quark production at the Tevatron and LHC energies could be of interest to verify self-similarity over a wide range of masses and different flavor content of produced particles.
and masses of heavy mesons is studied. We anticipate that the data on lowand high-pT inclusive spectra of the top-quark production at the Tevatron and LHC energies could be of interest to verify self-similarity over a wide range of masses and different flavor content of produced particles.
1. Introduction
The measurements of the top-quark transverse momentum distribution have been performed at the Fermilab Tevatron collider at 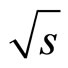 = 1800 and 1960 GeV by the CDF [1] and DØ [2] Collaborations, respectively. The integrated luminosities of CDF and DØ data samples are 106 pb–1 and 1 fb–1. The top-quark is the heaviest known elementary particle and was discovered at the Tevatron
= 1800 and 1960 GeV by the CDF [1] and DØ [2] Collaborations, respectively. The integrated luminosities of CDF and DØ data samples are 106 pb–1 and 1 fb–1. The top-quark is the heaviest known elementary particle and was discovered at the Tevatron 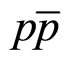 collider in 1995 by the CDF and DØ Collaborations [3,4] at a mass of around 170 GeV. It is expected [5-12] that the top physics is extremely important for scientific search for new phenomena.
collider in 1995 by the CDF and DØ Collaborations [3,4] at a mass of around 170 GeV. It is expected [5-12] that the top physics is extremely important for scientific search for new phenomena.
In the given paper we have analyzed the DØ data using the method known as z-scaling [13,14]. Main features of the approach in pp and 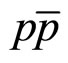 interactions at FNAL, CERN, and BNL (RHIC) energies were presented and discussed in [15,16]. Some results of analysis of the LHC data on the charged hadron [17],
interactions at FNAL, CERN, and BNL (RHIC) energies were presented and discussed in [15,16]. Some results of analysis of the LHC data on the charged hadron [17], 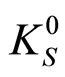 -meson [18], and jet [19,20] production are presented in [21-23]. The method allows us to perform systematic analysis of data on inclusive cross sections of hadrons, direct photons, and jets under different kinematic conditions. Scaling function
-meson [18], and jet [19,20] production are presented in [21-23]. The method allows us to perform systematic analysis of data on inclusive cross sections of hadrons, direct photons, and jets under different kinematic conditions. Scaling function  and scaling variable z are expressed via experimentally measurable quantities: inclusive and total inelastic cross sections, multiplicity density, momenta and masses of colliding and produced particles and using some physical parameters. The shape of the scaling function was found to be independent of the collision energy, multiplicity density of particles, detection angle and hadron type. The power behavior of function
and scaling variable z are expressed via experimentally measurable quantities: inclusive and total inelastic cross sections, multiplicity density, momenta and masses of colliding and produced particles and using some physical parameters. The shape of the scaling function was found to be independent of the collision energy, multiplicity density of particles, detection angle and hadron type. The power behavior of function 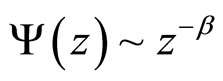 was established in high-z (high-pT) range. At low z (lowpT), saturation of the scaling function was found down to a value of
was established in high-z (high-pT) range. At low z (lowpT), saturation of the scaling function was found down to a value of 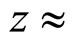 10−3 [16,22]. It has been concluded that z-scaling reflects self-similarity of the hadron structure, constituent interactions and hadronization process. The analyzed experimental data cover a wide range of the collision energies, transverse momenta and angles of the produced particles. The energy, angular and multiplicity independence of scaling function
10−3 [16,22]. It has been concluded that z-scaling reflects self-similarity of the hadron structure, constituent interactions and hadronization process. The analyzed experimental data cover a wide range of the collision energies, transverse momenta and angles of the produced particles. The energy, angular and multiplicity independence of scaling function 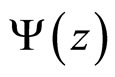 gives strong constraints on the values of parameters δ, c, and ε entering in definition of z. The parameter c which controls the behavior of
gives strong constraints on the values of parameters δ, c, and ε entering in definition of z. The parameter c which controls the behavior of 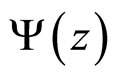 at low z has analogy with the “specific heat” of the produced medium associated with the inclusive particle production. The scaling in pp and
at low z has analogy with the “specific heat” of the produced medium associated with the inclusive particle production. The scaling in pp and 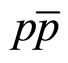 collisions is consistent with the constant value of c = 0.25. A possible change of this parameter could be assumed to be an indication of the phase transition of the matter produced in high energy collisions. The structure of the interacting objects produced at high momenta is characterized by parameter
collisions is consistent with the constant value of c = 0.25. A possible change of this parameter could be assumed to be an indication of the phase transition of the matter produced in high energy collisions. The structure of the interacting objects produced at high momenta is characterized by parameter  interpreted as a nucleon fractal dimension. The scaling is consistent with the constant value of δ = 0.5 for all types of the analyzed inclusive hadrons. The fragmentation process is parameterized in terms of dimension
interpreted as a nucleon fractal dimension. The scaling is consistent with the constant value of δ = 0.5 for all types of the analyzed inclusive hadrons. The fragmentation process is parameterized in terms of dimension  which increases together with the hadron mass.
which increases together with the hadron mass.
In this paper we have analyzed the data [2] on transverse momentum spectra of the top-quark production in 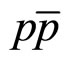 collisions at energy
collisions at energy  = 1960 GeV in the middle rapidity range obtained by the DØ Collaboration at the Tevatron. The measurements select the events with an isolated lepton having transverse momentum pT of at least 20 GeV/c and a pseudo-rapidity of
= 1960 GeV in the middle rapidity range obtained by the DØ Collaboration at the Tevatron. The measurements select the events with an isolated lepton having transverse momentum pT of at least 20 GeV/c and a pseudo-rapidity of 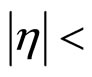 1.1 (e + jets) or
1.1 (e + jets) or 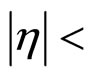 2.0 (μ + jets). A cut on the missing transverse energy of 20 GeV was applied. Furthermore at least four jets were required with pT > 20 GeV/c and
2.0 (μ + jets). A cut on the missing transverse energy of 20 GeV was applied. Furthermore at least four jets were required with pT > 20 GeV/c and 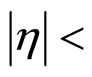 2.5, an additional cut of pT > 40 GeV/c was applied for the leading jet. Finally at least one jet needs to be identified as a b-jet. Additional constraints are used to reconstruct the event kinematics: the masses of two W bosons are constrained to 80.4 GeV. The masses of the two reconstructed top quarks are assumed to be equal.
2.5, an additional cut of pT > 40 GeV/c was applied for the leading jet. Finally at least one jet needs to be identified as a b-jet. Additional constraints are used to reconstruct the event kinematics: the masses of two W bosons are constrained to 80.4 GeV. The masses of the two reconstructed top quarks are assumed to be equal.
The results of analysis of the top inclusive cross sections are compared with Tevatron data [24-26] on J/ψ, D0B, and Υ particle spectra at 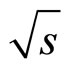 = 1960 and 1800 GeV in the z-presentation. We have verified the flavor independence of
= 1960 and 1800 GeV in the z-presentation. We have verified the flavor independence of 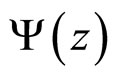 including the inclusive top-quark measurements in this region. A microscopic scenario of hadron production in the z-scaling approach is used to estimate the energy loss and recoil mass at a constituent level in the dependence on transverse momentum of an inclusive particle. This gives the specific dependence of the momentum fraction x1 characteristic for different types of produced hadrons. The pT-behavior of the fraction x1 for the top-quark production is compared with other particles.
including the inclusive top-quark measurements in this region. A microscopic scenario of hadron production in the z-scaling approach is used to estimate the energy loss and recoil mass at a constituent level in the dependence on transverse momentum of an inclusive particle. This gives the specific dependence of the momentum fraction x1 characteristic for different types of produced hadrons. The pT-behavior of the fraction x1 for the top-quark production is compared with other particles.
We expect that systematic measurements of the inclusive differential spectra of the top-quark as a function of the transverse momentum at LHC energies could give new information on self-similarity of the heavy flavor production in the super high energy domain.
2. z-Scaling
Here we follow the basic ideas of the z-scaling approach [15,16]. It is assumed that the collision of extended objects (hadrons, nuclei) at sufficiently high energies could be considered to be an ensemble of individual interactions of their constituents (partons, quarks, gluons). Structures of the colliding objects are characterized by parameters 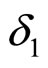 and
and . The constituents of the incoming objects (hadrons or nuclei) with masses M1, M2 carry away fractions x1, x2 of their momenta P1, P2. The inclusive particle has a fraction (denoted by
. The constituents of the incoming objects (hadrons or nuclei) with masses M1, M2 carry away fractions x1, x2 of their momenta P1, P2. The inclusive particle has a fraction (denoted by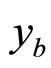 ) of the momentum of the object produced in the constituent collision in the observed direction. Its fragmentation is characterized by parameter
) of the momentum of the object produced in the constituent collision in the observed direction. Its fragmentation is characterized by parameter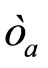 . The fragmentation in the recoil direction is described by parameter
. The fragmentation in the recoil direction is described by parameter 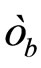 and momentum fraction
and momentum fraction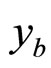 . Multiple interactions of the constituents are considered to be similar. This property reflects the self-similarity of the hadron interactions at the constituent level.
. Multiple interactions of the constituents are considered to be similar. This property reflects the self-similarity of the hadron interactions at the constituent level.
2.1. Momentum Fractions x1, x2, ya and yb
The elementary sub-process is considered to be a binary collision of the constituents with masses x1M1 and x2M2 resulting in the scattered and recoil objects with masses 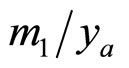 and
and 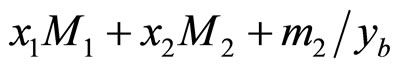 in the final state. The produced secondary objects transform into real particles after the constituent collisions. The registered particle with mass m1 and 4-momentum p is produced with its hadron counterpart with mass m2 carrying the momentum fractions of the produced recoil. The momentum conservation law of the constituent sub-process is written in the following form:
in the final state. The produced secondary objects transform into real particles after the constituent collisions. The registered particle with mass m1 and 4-momentum p is produced with its hadron counterpart with mass m2 carrying the momentum fractions of the produced recoil. The momentum conservation law of the constituent sub-process is written in the following form:
 (1)
(1)
Here MX is the recoil mass and
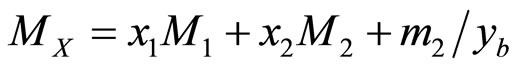 .
.
The production of the associated particle with mass m2 ensures conservation of the additive quantum numbers. Equation (1) is an expression of the locality of the hadron interaction at a constituent level. It represents a kinematic constraint on momentum fractions , and
, and 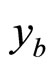 which determine the underlying elementary sub-process.
which determine the underlying elementary sub-process.
The structure of colliding objects and fragmentation of the systems formed in scattered and recoil directions are characterized by parameters , and
, and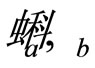 , respectively. The parameters are related with the corresponding momentum fractions by function
, respectively. The parameters are related with the corresponding momentum fractions by function
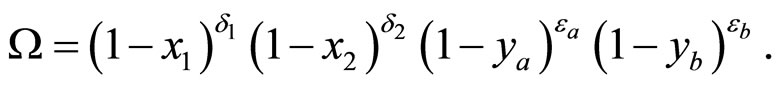 (2)
(2)
Quantity Ω is proportional to the relative number of all constituent configurations in the inclusive reaction, which contain the configuration defined by fractions 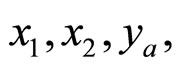 and
and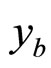 . The Ω is interpreted as a relative volume which occupies these configurations in the space of the momentum fractions. Parameters
. The Ω is interpreted as a relative volume which occupies these configurations in the space of the momentum fractions. Parameters , and
, and 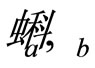 are taken as fractal dimensions in the parts of the space of the momentum fractions which correspond to the colliding objects and fragmentation processes, respectively. For the given values of
are taken as fractal dimensions in the parts of the space of the momentum fractions which correspond to the colliding objects and fragmentation processes, respectively. For the given values of , and
, and 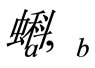 the fractions
the fractions  and
and 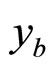 are determined in such a way to maximize the function Ω, simultaneously fulfilling condition (1).
are determined in such a way to maximize the function Ω, simultaneously fulfilling condition (1).
In the case of pp (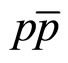 ) interactions we have
) interactions we have  and set
and set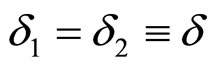 . It is assumed that the fragmentation of the objects moving in the scattered and recoil directions can be described by the same parameter
. It is assumed that the fragmentation of the objects moving in the scattered and recoil directions can be described by the same parameter 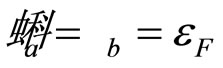 which depends on the type of the inclusive particle. The values of parameters
which depends on the type of the inclusive particle. The values of parameters 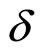 and
and 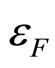 are determined according to the self-similarity requirements of experimental data in z-presentation. They were found to have constant values in pp and
are determined according to the self-similarity requirements of experimental data in z-presentation. They were found to have constant values in pp and 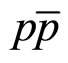 collisions at high energies.
collisions at high energies.
2.2. Scaling Variable z and Scaling Function Ψ(z)
The self-similarity of hadron interactions reflects the property that hadron constituents and their interactions are similar. The self-similarity variable z is defined as follows:
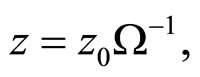 (3)
(3)
where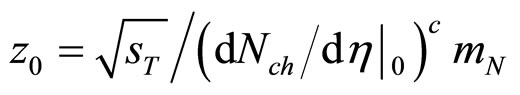 , and
, and 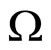 is the maximal value of (2) with condition (1). For the above inclusive reaction the quantity z is proportional to the transverse kinetic energy
is the maximal value of (2) with condition (1). For the above inclusive reaction the quantity z is proportional to the transverse kinetic energy 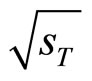 of the constituent subprocess consumed for the production of the inclusive particle and its counterpart with masses m1 and m2, respectively. The quantity
of the constituent subprocess consumed for the production of the inclusive particle and its counterpart with masses m1 and m2, respectively. The quantity 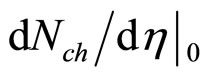 is the corresponding multiplicity density of charged particles produced in the central region of the reaction at the pseudo-rapidity
is the corresponding multiplicity density of charged particles produced in the central region of the reaction at the pseudo-rapidity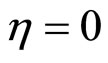 . Parameter c characterizes properties of the produced medium. It is interpreted as “specific heat”. The constant mN is taken to be a nucleon mass.
. Parameter c characterizes properties of the produced medium. It is interpreted as “specific heat”. The constant mN is taken to be a nucleon mass.
Scaling function 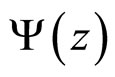 is expressed in terms of the experimentally measured inclusive cross section
is expressed in terms of the experimentally measured inclusive cross section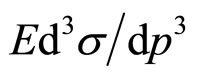 , the multiplicity density
, the multiplicity density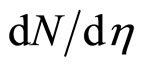 , and the total inelastic cross section
, and the total inelastic cross section 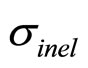 as follows [15]:
as follows [15]:
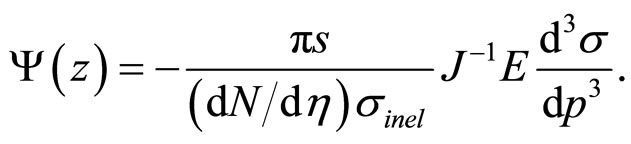 (4)
(4)
Here s is the square of the center-of-mass energy and J is the corresponding Jacobian. The multiplicity density 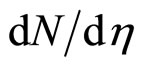 in (4) depends on the center-of-mass energy, centrality, and on the production angles at which the inclusive spectra were measured. The above expression can be rewritten in the central interaction region into the following form:
in (4) depends on the center-of-mass energy, centrality, and on the production angles at which the inclusive spectra were measured. The above expression can be rewritten in the central interaction region into the following form:
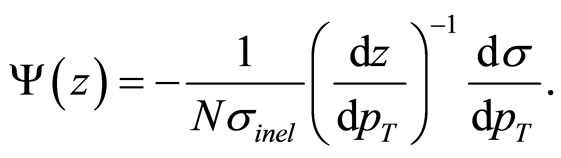 (5)
(5)
The scaling function is normalized as follows:
 (6)
(6)
It allows us to interpret 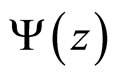 as a probability density of the production of the inclusive particle with the corresponding value of variable z.
as a probability density of the production of the inclusive particle with the corresponding value of variable z.
3. Flavor Independence of Ψ(z) and Self-Similarity of Top Production
The flavor independence of hadron production means that spectra of particles with a different flavor content can be described by universal scaling function 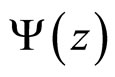 in z-presentation [15,16]. Our previous analysis is based on the observation that simultaneous energy, angular and multiplicity independence of the z-scaling for negative pions, kaons, and anti-protons produced in proton-proton collisions gives the same shape of the scaling function. The flavor independence of
in z-presentation [15,16]. Our previous analysis is based on the observation that simultaneous energy, angular and multiplicity independence of the z-scaling for negative pions, kaons, and anti-protons produced in proton-proton collisions gives the same shape of the scaling function. The flavor independence of 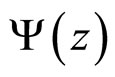 was also confirmed for other inclusive particles including the heavy quarkonia, J/ψ [24], and Υ [26], measured at the Tevatron energies
was also confirmed for other inclusive particles including the heavy quarkonia, J/ψ [24], and Υ [26], measured at the Tevatron energies 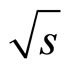 = 1960 and 1800 GeV. The property of
= 1960 and 1800 GeV. The property of  was observed at very small values of
was observed at very small values of 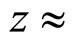 10−3. In the region
10−3. In the region 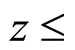 0.1 we observe a saturation of scaling function
0.1 we observe a saturation of scaling function  which can be approximated by a constant.
which can be approximated by a constant.
In this paper we analyze the data [2] on the differential cross section of the top-quark production measured by the DØ Collaboration at the Tevatron as a function of the transverse momentum pT at a middle rapidity. We have shown that the flavor independence of the z-presentation of hadron spectra is valid for the top-quark production as well. We exploit the scaling transformation
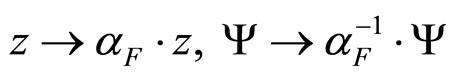 (7)
(7)
to compare the shape of scaling function 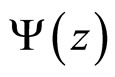 for different hadron species. Parameter
for different hadron species. Parameter  is the scale independent quantity. The transformation does not destroy the shape of
is the scale independent quantity. The transformation does not destroy the shape of . It preserves the normalization Equation (6) and the energy, angular and multiplicity independences of the z-presentation of particle spectra.
. It preserves the normalization Equation (6) and the energy, angular and multiplicity independences of the z-presentation of particle spectra.
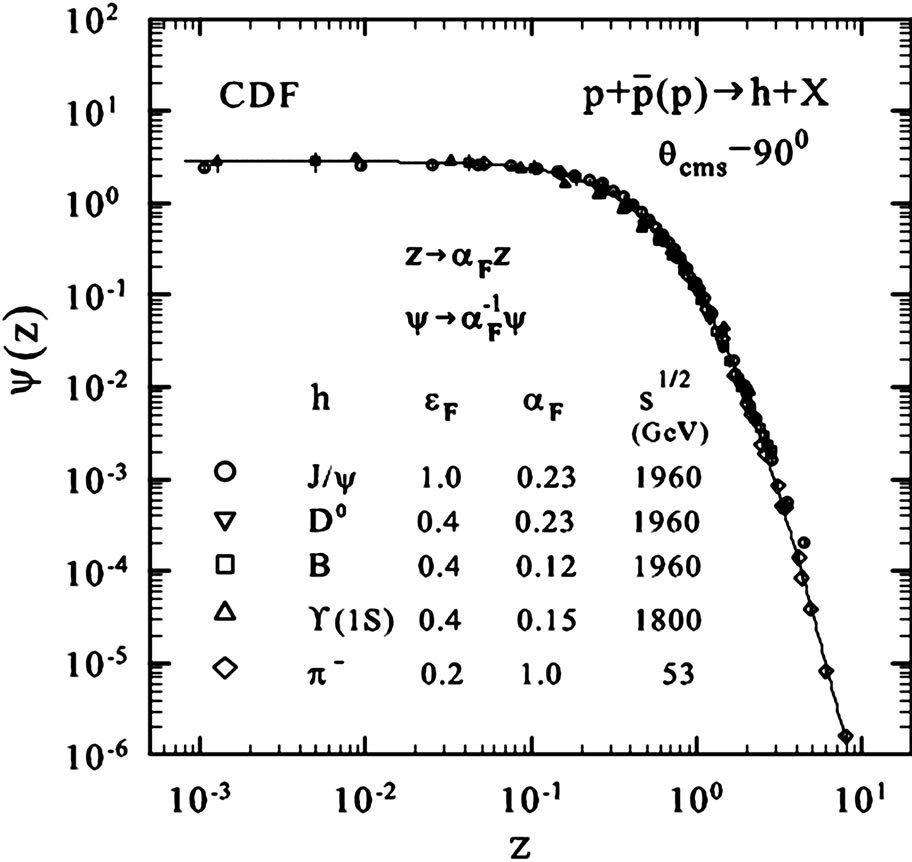
Figure 1(a) shows the z-presentation of the spectra of heavy hadrons (J/ψ, D0, B, and Υ) [24-26] obtained in  collisions at the Tevatron energies
collisions at the Tevatron energies  = 1960 and 1800 GeV in the central rapidity region. The experimental data are shown by symbols. The data include measurements up to small transverse momenta (pT ≈ 125 MeV/c for charmonia, pT ≈ 290 MeV/c for bottomia, and pT ≈ 500 MeV/c for B-mesons). The data on the
= 1960 and 1800 GeV in the central rapidity region. The experimental data are shown by symbols. The data include measurements up to small transverse momenta (pT ≈ 125 MeV/c for charmonia, pT ≈ 290 MeV/c for bottomia, and pT ≈ 500 MeV/c for B-mesons). The data on the  -meson spectra at
-meson spectra at  = 53 GeV [27] are used as reference data. As seen from Figure 1(a) the shape of scaling function is the same for hadrons with light and heavy flavors produced in pp and
= 53 GeV [27] are used as reference data. As seen from Figure 1(a) the shape of scaling function is the same for hadrons with light and heavy flavors produced in pp and 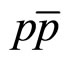 collisions in the range z = 0.001 - 4. This is indicated by the solid line. One can see that distributions of different hadrons are sufficiently well described with a single curve over a wide z-range (0.001 - 10). Function
collisions in the range z = 0.001 - 4. This is indicated by the solid line. One can see that distributions of different hadrons are sufficiently well described with a single curve over a wide z-range (0.001 - 10). Function  changes more than by six orders of magnitude in this region. The values of parameters
changes more than by six orders of magnitude in this region. The values of parameters 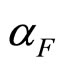 and
and 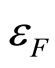 shown in this Figure are consistent with the energy, angular and multiplicity independences of the z-presentation of the spectra for different hadrons. The parameters were found to be independent of kinematic variables (
shown in this Figure are consistent with the energy, angular and multiplicity independences of the z-presentation of the spectra for different hadrons. The parameters were found to be independent of kinematic variables (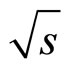 , pT, and
, pT, and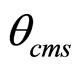 ). The scale factors
). The scale factors 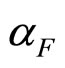 are constants. It allows us to describe z-presentation of the spectra for different hadron species with a single function. The collapse of data points onto a single curve corresponds to the estimated errors of
are constants. It allows us to describe z-presentation of the spectra for different hadron species with a single function. The collapse of data points onto a single curve corresponds to the estimated errors of  at the level of 20%.
at the level of 20%.
Figure 1(b) demonstrates the results of analysis of the Tevatron data [2] on the top-quark spectra measured by the DØ Collaboration in 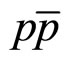 collisions at the energy
collisions at the energy 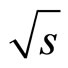 = 1960 GeV and the central rapidity range in zpresentation. The solid line is the same curve as depicted in Figure 1(a). Scaling function
= 1960 GeV and the central rapidity range in zpresentation. The solid line is the same curve as depicted in Figure 1(a). Scaling function 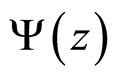 for the topquark distribution was calculated according to Equation (5). The vertical errors are given by a quadratic sum of the statistical uncertainties and the systematic uncertainties on the shape of the cross section in each pT-bin. The
for the topquark distribution was calculated according to Equation (5). The vertical errors are given by a quadratic sum of the statistical uncertainties and the systematic uncertainties on the shape of the cross section in each pT-bin. The
 (a)
(a)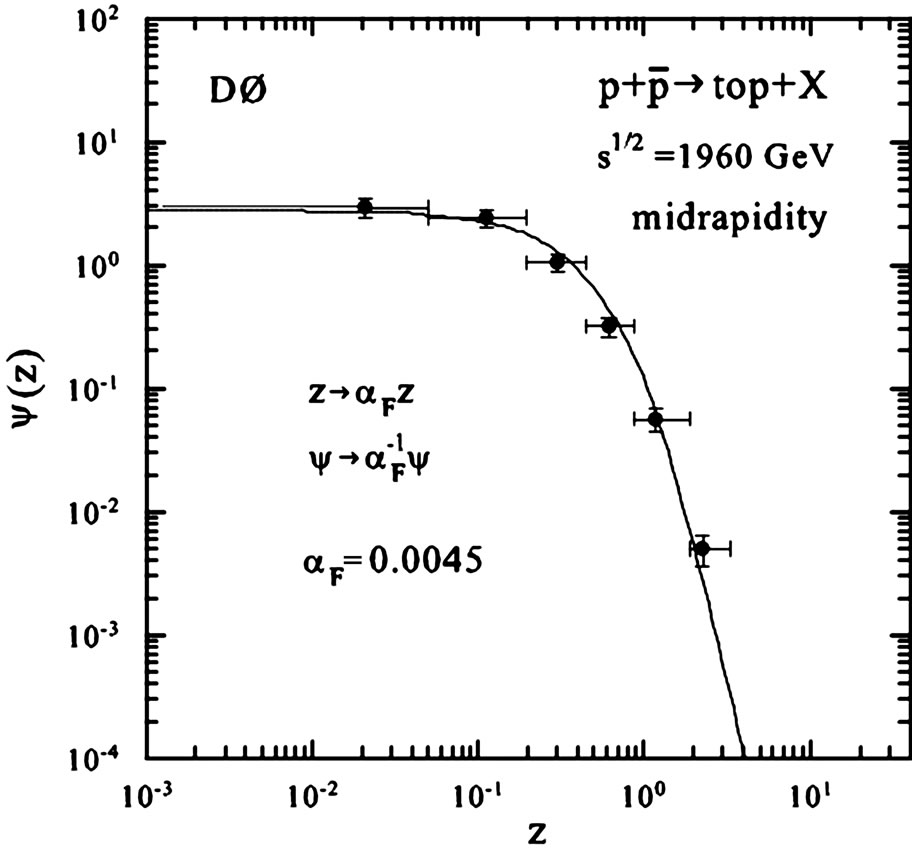 (b)
(b)
Figure 1. The flavor independence of z-scaling. The spectra of (a) J/ψ, D0, B, Υ mesons; and (b) top-quarks produced in  collisions at the Tevatron in z-presentation. The spectra of π– mesons were measured in pp collisions at ISR. The data are taken from [2,24-27]. The solid line in (b) is the same as in (a).
collisions at the Tevatron in z-presentation. The spectra of π– mesons were measured in pp collisions at ISR. The data are taken from [2,24-27]. The solid line in (b) is the same as in (a).
horizontal errors refer to the width of the bins. The condition (6) is satisfied with the normalization 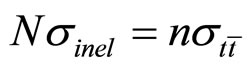 and n = 2. This corresponds to two entries per event with the total normalization to the
and n = 2. This corresponds to two entries per event with the total normalization to the 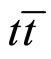 production cross section
production cross section  = 8.31 pb [2].
= 8.31 pb [2].
The values of the fractal dimension 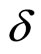 = 0.5 and “specific heat” c = 0.25 are the same as used in the previous analyses of the inclusive spectra [15,16,21]. We have set
= 0.5 and “specific heat” c = 0.25 are the same as used in the previous analyses of the inclusive spectra [15,16,21]. We have set 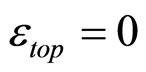 in the case of the top-quark since no energy loss is assumed in the elementary
in the case of the top-quark since no energy loss is assumed in the elementary 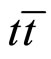 production process. This choice corresponds to
production process. This choice corresponds to 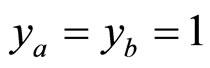 in the whole pT-range. The value of
in the whole pT-range. The value of  in the transformation (7) is found to be
in the transformation (7) is found to be 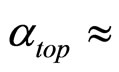 0.0045. No additional parameters were used.
0.0045. No additional parameters were used.
As it is seen from Figure 1(b), the z-presentation of the top-quark transverse momentum distribution follows the shape of the z-scaling in pp (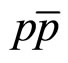 ) collisions for other particles sufficiently well. Note that the top-spectrum is in the limited kinematic region and the error bars of the data are large enough. We would like to stress that existing analyses were performed with pT-distributions of the inclusive cross sections
) collisions for other particles sufficiently well. Note that the top-spectrum is in the limited kinematic region and the error bars of the data are large enough. We would like to stress that existing analyses were performed with pT-distributions of the inclusive cross sections  which reveal strong dependence on the energy, angle, multiplicity and type of the produced particles. Based on the above comparison we have concluded that the Tevatron data on inclusive spectra of the top-quark production measured by the DØ Collaboration support the flavor independence of scaling function
which reveal strong dependence on the energy, angle, multiplicity and type of the produced particles. Based on the above comparison we have concluded that the Tevatron data on inclusive spectra of the top-quark production measured by the DØ Collaboration support the flavor independence of scaling function 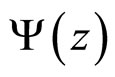 over the range of z = 0.02 - 2. This result gives us an indication on self-similarity of top-quark production in
over the range of z = 0.02 - 2. This result gives us an indication on self-similarity of top-quark production in 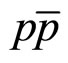 collisions at
collisions at  = 1960 GeV.
= 1960 GeV.
The determination method of the momentum fractions allows us to analyze kinematics of the constituent interactions in the framework of the developed approach. Unlike other particles, the null value of εtop means that the energy loss of the top-quark production is zero or negligible. This result is expressed by condition 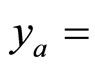
 and by the value of recoil mass MX which is practically equal to the mass of the top-quark. The kinematics of the underlying sub-process is fully determined by momentum fractions x1 and x2 in this case. The fractions characterize the amount of the energy (momentum) of the incoming protons (antiprotons) carried by the interacting constituents which cause the inclusive particle production. In the general case of other particles, x1 and x2 are functions of ya and yb [15]. For the central interaction region, x1 and x2 are equal to each other. A comparison of fraction x1 for the top-quark production with other heavy particles is shown in Figure 2" target="_self"> Figure 2. The illustration is presented as a function of the scaled transverse momentum
and by the value of recoil mass MX which is practically equal to the mass of the top-quark. The kinematics of the underlying sub-process is fully determined by momentum fractions x1 and x2 in this case. The fractions characterize the amount of the energy (momentum) of the incoming protons (antiprotons) carried by the interacting constituents which cause the inclusive particle production. In the general case of other particles, x1 and x2 are functions of ya and yb [15]. For the central interaction region, x1 and x2 are equal to each other. A comparison of fraction x1 for the top-quark production with other heavy particles is shown in Figure 2" target="_self"> Figure 2. The illustration is presented as a function of the scaled transverse momentum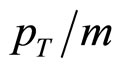 . One can see the x1 growth with
. One can see the x1 growth with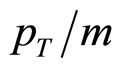 . The value of x1 is larger for the production of heavy particles as compared with the light ones. The exception for J/ψ meson was observed (see discussed in [16]). It is a consequence of the relatively large value of
. The value of x1 is larger for the production of heavy particles as compared with the light ones. The exception for J/ψ meson was observed (see discussed in [16]). It is a consequence of the relatively large value of  related
related
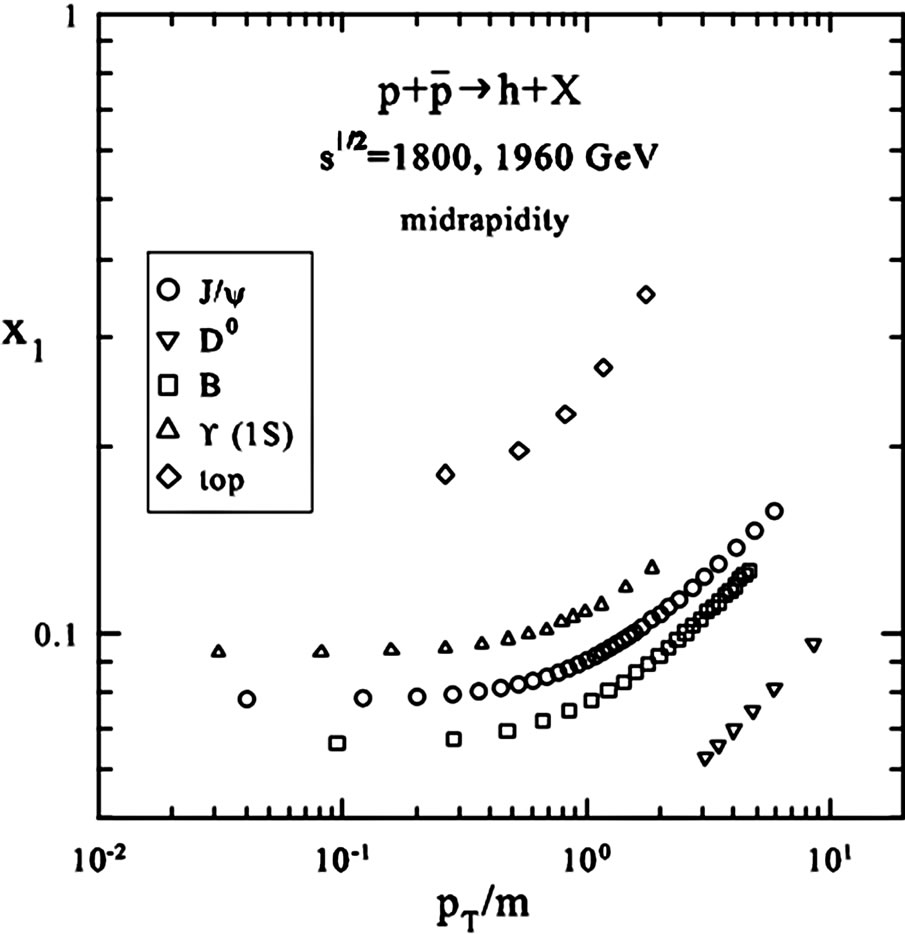
Figure 2. The momentum fraction x1 as a function of the scaled transverse momentum pT/m of hadrons produced in  collisions at
collisions at  = 1800 and 1960 GeV in the middle rapidity region.
= 1800 and 1960 GeV in the middle rapidity region.
with extra large energy dissipation in the final state accompanied by production of this particle. For a fixed value of  the fraction x1 decreases while increasing collision energy
the fraction x1 decreases while increasing collision energy . The kinematic limit of the reaction
. The kinematic limit of the reaction  corresponds to
corresponds to 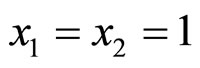 at any collision energy and for any type of the inclusive particle.
at any collision energy and for any type of the inclusive particle.
4. Conclusions
We have presented the results of analysis of the data on inclusive spectra of the top-quark production in 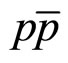 collisions at the energy
collisions at the energy 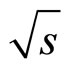 = 1960 GeV measured by the DØ Collaboration at the Tevatron. The transverse momentum spectra in z-presentation are compared with the data obtained for the heavy mesons J/ψ, D0, B, and Υ at the Tevatron energies
= 1960 GeV measured by the DØ Collaboration at the Tevatron. The transverse momentum spectra in z-presentation are compared with the data obtained for the heavy mesons J/ψ, D0, B, and Υ at the Tevatron energies  = 1960 and 1800 GeV in the central rapidity range. Based on the results presented here we conclude that the data on the transverse momentum distribution of the top-quark production in
= 1960 and 1800 GeV in the central rapidity range. Based on the results presented here we conclude that the data on the transverse momentum distribution of the top-quark production in  collision are in good agreement with flavor independence of the z-scaling. The result also supports the energy independence of the scaling function in the middle rapidity region. A tendency to
collision are in good agreement with flavor independence of the z-scaling. The result also supports the energy independence of the scaling function in the middle rapidity region. A tendency to 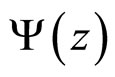 saturation at low z for the top-quark production is confirmed as well. The momentum fraction x1 of the incoming protons for the top-quark was compared with the corresponding values for the heavy mesons measured at the Tevatron. Though production of the top-quark is characterized by no energy loss and constant recoil mass
saturation at low z for the top-quark production is confirmed as well. The momentum fraction x1 of the incoming protons for the top-quark was compared with the corresponding values for the heavy mesons measured at the Tevatron. Though production of the top-quark is characterized by no energy loss and constant recoil mass , the fraction x1 reveal similar dependences on the scaled transverse momentum
, the fraction x1 reveal similar dependences on the scaled transverse momentum 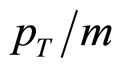 as for the heavy mesons.
as for the heavy mesons.
We assume that the data on the top-quark differential inclusive cross section over a wider range of pT and collision energy  at the Tevatron and LHC could be of interest to verify the flavor independence of z-scaling and self-similarity of top-quark production.
at the Tevatron and LHC could be of interest to verify the flavor independence of z-scaling and self-similarity of top-quark production.
5. Acknowledgements
These investigations have been supported by the IRP AVOZ10480505, by the Ministry of Education of the Czech Republic grants LA08002, LA08015.
REFERENCES
- T. Affolder, et al., “Measurement of the Top Quark pT Distribution,” Physical Review Letters, Vol. 87, No. 10, 2001, Article ID: 102001. doi:10.1103/PhysRevLett.87.102001
- V. M. Abazov et al., “Dependence of the tbart Production Cross Section on the Transverse Momentum of the Top Quark,” Physics Letters B, Vol. 693, No. 5, 2010, pp. 515-521. doi:10.1016/j.physletb.2010.09.011
- F. Abe, et al., “Observation of Top Quark Production in pbarp Collisions with Collider Detector at Fermilab,” Physical Review Letters, Vol. 74, No. 14, 1995, pp. 2626- 2631.
- S. Abachi et al., “Observation of the Top Quark,” Physical Review Letters, Vol. 74, No.14, 1995, pp. 2632-2637.
- E. Laenen, “Top Physics: theoretical aspects,” Physics at the LHC 2011, Perugia, 5-11 June 2011. http://www.pg.infn.it/plhc2011/index.html
- A. Garcia-Bellido, “Top quark physics at the Tevatron,” Physics at LHC 2011, Perugia, 6-11 June, 2011. http://www.pg.infn.it/plhc2011/index.html
- Y. Peters, “Top Quark Properties,” XXXI PHYSICS IN COLLISION, Vancouver, 28 August-1 September 2011. http://arxiv.org/abs/1112.0451
- E. Shabalina, “Particle Physics and Cosmology,” 2010. http://confs.obspm.fr/Blois2010/index.html
- R. Kehoe, M. Narain, A. Kumar, “Review of Top Quark Physics Results,” International Journal of Modern Physics A, Vol. 23, No. 3-4, 2008, pp. 353-470. doi:10.1142/S0217751X08039293
- W. Wagner, “Top Quark Physics in Hadron Collisions,” Reports on Progress in Physics, Vol. 68, No. 10, 2005, pp. 2409-2494. doi:10.1088/0034-4885/68/10/R03
- A. Quadt, “Top Quark Physics at Hadron Colliders,” European Physical Journal C, Vol. 48, No. 3, 2006, pp. 835-1000. doi:10.1140/epjc/s2006-02631-6
- E. W. N. Glover, et al., “Top Quark Physics at Colliders,” Acta Physica Polonica B, Vol. 35, No. 11, 2004, pp. 2671-2694.
- I. Zborovský, Yu. Panebratsev, M. Tokarev and G. Škoro, “z-Scaling in Hadron-Hadron Collisions at High Energies,” Physical Review D, Vol. 54, No. 9, 1996, pp. 5548- 5557. doi:10.1103/PhysRevD.54.5548
- M. Tokarev, I. Zborovský, Yu. Panebratsev and G. Škoro, “A-Dependence of z-Scaling,” International Journal of Modern Physics A, Vol. 16, No. 7, 2001, pp. 1281-1301. doi:10.1142/S0217751X01003391
- I. Zborovský and M. V. Tokarev, “Generalized z-Scaling in Proton-Proton Collisions at High Energies,” Physical Review D, Vol. 75, No. 9, 2007, Article ID: 094008.
- I. Zborovský and M. V. Tokarev, “New Properties of zScaling: Flavor Independence and Saturation at Low z,” International Journal of Modern Physics A, Vol. 24, No. 7, 2009, pp. 1417-1442. doi:10.1142/S0217751X09042992
- V. Khachatryan, et al., “Transverse Momentum and Pseudorapidity Distributions of Charged Hadrons in pp Collisions at
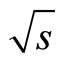 = 0.9 and 2.36 TeV,” Journal of High Energy Physics, Vol. 02, 2010, Article ID: 041.
= 0.9 and 2.36 TeV,” Journal of High Energy Physics, Vol. 02, 2010, Article ID: 041. - V. Khachatryan, et al., “Strange Particle Production in pp Collisions at
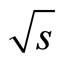 = 0.9 and 7 TeV,” Journal of High Energy Physics, Vol. 5, 2011, Article ID: 064.
= 0.9 and 7 TeV,” Journal of High Energy Physics, Vol. 5, 2011, Article ID: 064. - S. Chatrchyan, et al., “Measurement of the Inclusive Jet Cross Section in pp Collisions at
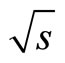 =7 TeV,” Physical Review Letters, Vol. 107, No. 13, 2011, Article id: 132001.
=7 TeV,” Physical Review Letters, Vol. 107, No. 13, 2011, Article id: 132001. - J. Zhang (for ATLAS Collaboration), XIX International Workshop DIS2011, 11-15 April 2011, Newport News. http://conferences.jlab.org/DIS2011/
- M. V. Tokarev and I. Zborovský, “On Saturation of Charged hadron Production in pp Collisions at LHC,” Journal of Physics G: Nuclear and Particle Physics, Vol. 37, No. 8, 2010, Article id: 085008. doi:10.1088/0954-3899/37/8/085008
- M. V. Tokarev and I. Zborovský, “Energy Loss in Hadron Production in pp and Heavy Ion Collisions,” Nuclear Physics B, Vol. 219-220, 2011, pp. 301-304. doi:10.1016/j.nuclphysbps.2011.10.116
- M. Tokarev and I. Zborovský, “First Test of z-Scaling in Hadron and Jet Production at LHC,” XLI International Symposium on Multiparticle Dynamics (ISMD2011), Hiroshima, 26-30 September 2011. http://home.hiroshima-u.ac.jp/ismd2011/
- D. Acosta, et al., “Measurement of the J/ψ meson and bhadron Production Cross Sections in p-barp Collisions at
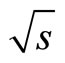 = 1960 GeV,” Physical Review D, Vol. 71, 2005, Article ID: 032001. doi:10.1103/PhysRevD.71.032001
= 1960 GeV,” Physical Review D, Vol. 71, 2005, Article ID: 032001. doi:10.1103/PhysRevD.71.032001 - D. Acosta, et al., “Measurement of Prompt Charm Meson Production Cross Sections in p-barp Collisions at
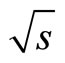 = 1:96 TeV,” Physical Review Letters, Vol. 91, No. 24, 2003, Article ID: 241804. doi:10.1103/PhysRevLett.91.241804
= 1:96 TeV,” Physical Review Letters, Vol. 91, No. 24, 2003, Article ID: 241804. doi:10.1103/PhysRevLett.91.241804 - D. Acosta, et al., “Y Production and Polarization in p-bar p Collisions at
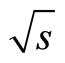 = 1.8 TeV,” Physical Review Letters, Vol. 88, No.16, 2002, Article ID: 161802. doi:10.1103/PhysRevLett.88.161802
= 1.8 TeV,” Physical Review Letters, Vol. 88, No.16, 2002, Article ID: 161802. doi:10.1103/PhysRevLett.88.161802 - B. Alper, et al., “Production Spectra of
 at Large Angles in Proton-Proton Collisions in the CERN Intersecting Storage Rings,” Nuclear Physics B, Vol. 100, No. 2, 1975, pp. 237-290. doi:10.1016/0550-3213(75)90618-5
at Large Angles in Proton-Proton Collisions in the CERN Intersecting Storage Rings,” Nuclear Physics B, Vol. 100, No. 2, 1975, pp. 237-290. doi:10.1016/0550-3213(75)90618-5

