Applied Mathematics
Vol.06 No.08(2015), Article ID:58323,8 pages
10.4236/am.2015.68127
Local Study of Scalar Curvature of Cyclic Surfaces Obtained by Homothetic Motion of Lorentzian Circle
M. M. Wageeda1, E. M. Solouma2
1Department of Mathematics, Faculty of Science, Aswan University, Aswan, Egypt
2Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef, Egypt
Email: wageeda76@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 June 2015; accepted 24 July 2015; published 27 July 2015
ABSTRACT
In this paper we consider the homothetic motion of Lorentzian circle by studying the scalar curvature for the corresponding cyclic surface locally. We prove that if the scalar curvature 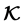 is constant, then
is constant, then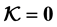 . We describe the equations that govern such surfaces.
. We describe the equations that govern such surfaces.
Keywords:
Minkowski Space, Cyclic Surfaces, Homothetic Motion, Scalar Curvature

1. Introduction
Homothetic motion is general form of Euclidean motion. It is crucial that homothetic motions are regular motions. These motions have been studied in kinematic and differential geometry in recent years. An equiform transformation in the n-dimensional Euclidean space  is an affine transformation whose linear part is composed from an orthogonal transformation and a homothetical transformation add see [1] -[3] . Such an equiform transformation maps points
is an affine transformation whose linear part is composed from an orthogonal transformation and a homothetical transformation add see [1] -[3] . Such an equiform transformation maps points 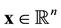 according to
according to
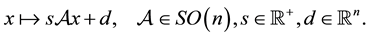 (1)
(1)
The number s is called the scaling factor. A homothetic motion is defined if the parameters of (1), including s, are given as functions of a time parameter t. Then a smooth one-parameter equiform motion moves a point x via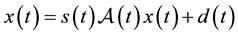 . The kinematic corresponding to this transformation group is called similarity kinematic. See [4] . Recently, the similarity kinematic geometry has been used in computer vision and reverse engineering of geometric models such as the problem of reconstruction of a computer model from an existing object which is known (a large number of) data points on the surface of the technical object [5] [6] . Abdel-All and Hamdoon studied a cyclic surface in
. The kinematic corresponding to this transformation group is called similarity kinematic. See [4] . Recently, the similarity kinematic geometry has been used in computer vision and reverse engineering of geometric models such as the problem of reconstruction of a computer model from an existing object which is known (a large number of) data points on the surface of the technical object [5] [6] . Abdel-All and Hamdoon studied a cyclic surface in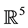 . In this sense, they proved that such surface in
. In this sense, they proved that such surface in  is in general contained in a canal hypersurface [7] . Solouma ( [8] - [10] ) studied locally some geometric problems on surfaces obtained by the equiform motion up to the first order. In Minkowski (semi-Euclidean) space, hyperbolas (Lorentzian circles) play role in Euclidean space [11] .
is in general contained in a canal hypersurface [7] . Solouma ( [8] - [10] ) studied locally some geometric problems on surfaces obtained by the equiform motion up to the first order. In Minkowski (semi-Euclidean) space, hyperbolas (Lorentzian circles) play role in Euclidean space [11] .
In this work we consider the homothetic motion of the hyperbolas(Lorentzian circles) . Let
. Let 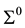 and
and 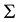 be two copies of Euclidean space
be two copies of Euclidean space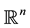 . Under a one-parameter homothetic motion of moving space
. Under a one-parameter homothetic motion of moving space 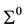 with respect to fixed space
with respect to fixed space , we consider
, we consider 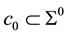 which is moved according homothetic motion. The point paths of the Lorentzian circle generate a cyclic surface X, containing the position of the starting Lorentzian circle. At any moment, the infinitesimal transformations of the motion will map the points of the Lorentzian circle
which is moved according homothetic motion. The point paths of the Lorentzian circle generate a cyclic surface X, containing the position of the starting Lorentzian circle. At any moment, the infinitesimal transformations of the motion will map the points of the Lorentzian circle 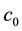 into the velocity vectors whose end points will form an affine image of
into the velocity vectors whose end points will form an affine image of 




Let 







The proof of our results involves explicit computations of the scalar curvature 












This paper is organized as follows: In Section 2, we obtain the expression of the scalar curvature 




2. Scalar Curvature of Cyclic Surfaces
In two copies





Under a one-parameter homothetic motion of 




where 




system. For varying t and fixed



where 
As homothetic motion has an invariant point, we can assume without loss of generality that the moving frame 


Thus
where








or in the equivalent form

For any fixed t in the above expression (3), we generally get an ellipse centered at the point

where


A straightforward computation leads to the coefficients of the first fundamental form defined by





is the sign matrix. Then we get
Under the conditions (4) a computation yields

and

The Christoffel symbols of the second kind are defined by
where




Although the explicit computation of the scalar curvature 


The assumption of the constancy of the scalar curvature 

Equation (8) means that if we write it as a linear combination of the functions 

describe all cyclic surfaces with constant scalar curvature obtained by the homothetic motion of the Lorentzian circle

We distinguish the cases 

3. Cyclic Surfaces with K = 0
In this section we assume that 


We distinguish different cases that fill all possible cases (Note that we have all solutions by using the symbolic program Mathematica under the condition
3.1. Case
At 











Theorem 3.1. Let 


1)
2)
In particular, if 

3.2. Case


We have two possibilities:
1) If 





coefficients 

conditions
2) If 





the coefficients 

Theorem 3.2. Let 
1) Assume 


2) Assume 


3.3. Case
If







Theorem 3.3. Let 


1)
2)
4. Cyclic Surfaces with K ¹ 0
In this section we assume that the scalar curvature 



Following the same scheme as in the case 



1) CASE



If
1.


2.


3.


From (1), (2) and (3) we have


4.




If
2) CASE
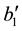

1. If 



2. If 



3) CASE


Theorem 4.1. Let 
and given by (3) under condition (4). Assume that

on the surface if and only if the following conditions hold:
5. Examples of a Cyclic Surfaces with K = 0 and K ¹ 0
In this section, we construct two examples of a cyclic surfaces 






Example 1. Case

We assume 

Theorem 3.3 says that





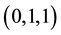

Figure 1. In (a), we have a piece of a cyclic surface foliated by a Lorentzian circle in axonometric view 


and
and both 


Example 2. Case

Let 

Theorem 4.1 says that 


axonometric viewpoint

Figure 2. In (a), we have a piece of a cyclic surface foliated by a Lorentzian circle in axonometric view 


and
and both 


Cite this paper
M. M.Wageeda,E. M.Solouma, (2015) Local Study of Scalar Curvature of Cyclic Surfaces Obtained by Homothetic Motion of Lorentzian Circle. Applied Mathematics,06,1344-1352. doi: 10.4236/am.2015.68127
References
- 1. Do Carmo, M. (1976) Differential Geometry of Curves and Surfaces. Prentice-Hall Inc. Englewood Cliffs, New Jersey.
- 2. Gordon, V.O. and Sement Sov, M.A. (1980) A Course in Descriptive Geometry. Mir Publishers, Moscow.
- 3. Jagy, W. (1998) Sphere Foliated Constant Mean Curvature Submanifolds. The Rocky Mountain Journal of Mathematics, 28, 983-1015.
http://dx.doi.org/10.1216/rmjm/1181071750 - 4. Bottema, O. and Roth, B. (1990) Theoretical Kinematic. Dover Publications Inc., New York.
- 5. Odehnal, B., Pottmann, H. and Wallner, J. (2006) Equiform Kinematics and the Geometry of Line Elements. Beiträge zur Algebra und Geometrie, 47, 567-582.
- 6. Pottmann, H. and Wallner, J. (2001) Computational Line Geometry. Springer Heidelberg Dordrecht, London, New York.
- 7. Abdel-All, N.H. and Hamdoon, F.M. (2004) Cyclic Surfaces in E5 Generated by Equiform Motions. Journal of Geometry, 79, 1-11.
http://dx.doi.org/10.1007/s00022-003-1682-2 - 8. Solouma, E.M. (2015) Three Dimensional Surfaces Foliated by an Equiform Motion of Pseudohyperbolic Surfaces in . JP Journal of Geometry and Topology, Accepted (To appear).
- 9. Solouma, E.M. (2012) Local Study of Scalar Curvature of Two-Dimensional Surfaces Obtained by the Motion of Circle. Applied Mathematics and Computation, 219, 3385-3394.
http://dx.doi.org/10.1016/j.amc.2012.09.066 - 10. Solouma, E.M., et al. (2007) Three Dimensional Surfaces Foliated by Two Dimensional Spheres. Journal of the Egyptian Mathematical Society, 1, 101-110.
- 11. O’Neill, B. (1983) Semi-Riemannian Geometry with Application to Relativity. Academic Press, New York and London.









































