Applied Mathematics
Vol.05 No.21(2014), Article ID:52266,4 pages
10.4236/am.2014.521326
Integral Inequalities of Gronwall-Bellman Type
Zareen A. Khan
Department of Mathematics, Princess Noura Bint Abdurehman University, Riyadh, KSA
Email: dr.zareenkhan@ymail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 September 2014; revised 21 October 2014; accepted 8 November 2014
ABSTRACT
The goal of the present paper is to establish some new approach on the basic integral inequality of Gronwall-Bellman type and its generalizations involving function of one independent variable which provides explicit bounds on unknown functions. The inequalities given here can be used as tools in the qualitative theory of certain partial differential and integral equations.
Keywords:
Integral Inequalities, One Independent Variable, Partial Differential Equations, Nondecreasing, Nonincreasing

1. Introduction
The Gronwall type integral inequalities provide a necessary tool for the study of the theory of differential equations, integral equations and inequalities of the various types. Some applications of this result can be used to the study of existence, uniqueness theory of differential equations and the stability of the solution of linear and nonlinear differential equations. During the past few years, several authors have established several Gronwall type integral inequalities in one or two independent real variables [1] -[15] . Of course, such results have application in the theory of partial differential equations and Volterra integral equations.
Closely related to the foregoing first-order ordinary differential operators is the following result of Bellman [11] : If the functions 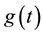 and
and 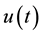 are nonnegative for
are nonnegative for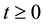 , and if
, and if , the inequality
, the inequality
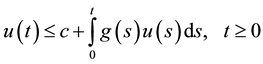
implies that
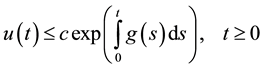 (1.1)
(1.1)
Our aim in this paper is to establish new explicit bounds on some basic integral inequalities of one independent variable which will be equally important in handling the inequality (1.1). Given application in this paper is also illustrating the usefulness of our result.
2. Main Results
Lemma 2.1: Let 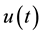 and
and 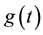 be nonnegative continuous functions defined for
be nonnegative continuous functions defined for . Let
. Let  defined for
defined for 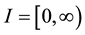 and also
and also 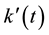 be nonnegative continuous functions defined for
be nonnegative continuous functions defined for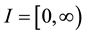 . If
. If
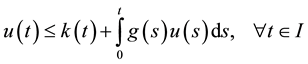 (2.1)
(2.1)
Then
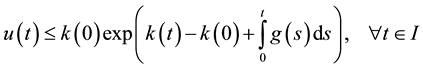 (2.2)
(2.2)
Proof: Define a function 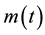 by the right-hand side of (2.1), such that
by the right-hand side of (2.1), such that

where

Then

Differentiating both sides of (2.3) with respect to t, we get
By using (2.5) and since

Integrating both sides of (2.6) from 0 to t and also using (2.4), we observe that

From (2.5) and (2.7), we get the required inequality (2.2).
Theorem 2.2: Let








Then

Proof: Define a function 

where

Then

Differentiating both sides of (2.10) with respect to t, we get
By using (2.12), the above equation can be restated as

where

and

Again differentiating both sides of (2.14) with respect to x and using (2.13) and using the fact that

By applying Lemma 2.1 implies the estimation of 

By substituting (2.17) in (2.13), we have
Integrating both sides of the above inequality from 0 to t and also using (2.11), we observe that

From (2.12) and (2.18), we get the required inequality (2.9). This completes the proof.
Theorem 2.3: Let





Then
Proof: The proof of Theorem 2.3 is the same as the proof of Theorem 2.2 and by applying the Lemma 2.1 with suitable modifications.
3. Application
As an application, let us consider the bound for the solution of Volterra integral equation of the form

where x, f and g are the elements of Rn, 




Define

and

Also let


Then
Proof: Taking absolute value of the both sides of (3.1), we get

By substituting from (3.2), (3.3), (3.4) and (3.5) in (3.6), we have
The remaining proof will be the same as the proof of Theorem 2.2 with suitable modifications. We note that Theorem 2.2 can be used to study the stability, boundedness and continuous dependence of the solutions of (3.1).
4. Conclusion
We finally mention that the integral inequalities obtained in this paper allow us to study the stability, boundedness and asymptotic behavior of the solutions of a class of more general partial differential and integral equations.
References
- Abdeldaim, A. and Yakout, M. (2011) On Some New Integral Inequalities of Gronwall-Bellman-Pachpatte Type. Applied Mathematics and Computation, 217, 7887-7899. http://dx.doi.org/10.1016/j.amc.2011.02.093
- Pachpatte, B.G. (2001) On Some Fundamental Integral Inequalities and Their Discrete Analogues. Journal of Inequalities in Pure and Applied Mathematics, 2, Article 15.
- Pachpatte, B.G. (1994) On Some Fundamental Integral Inequalities Arising in the Theory of Differential Equations. Chinese Journal of Mathematics, 22, 261-273.
- Pachpatte, B.G. (1996) Comparison Theorems Related to a Certain Inequality Used in the Theory of Differential Equations. Soochow Journal of Mathematics, 22, 383-394.
- Langenhop, C.E. (1960) Bounds on the Norm of a Solution of a General Differential Equation. Proceedings of the American Mathematical Society, 11, 795-799.
- Bainov, D. and Simeonov, P. (1992) Integral Inequalities and Applications. Kluwer Academic Publishers, Dordrecht.
- Mitrinovíc, D.S., Pěcaríc, J.E. and Fink, A.M. (1991) Inequalities Involving Functions and Their Integrals and Derivatives. Kluwer Academic Publishers, Dordrecht.
- Beckenbach, E.F. and Bellman, R. (1961) Inequalities. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-3-642-64971-4
- Bihari, I. (1956) A Generalization of a Lemma of Bellman and Its Application to Uniqueness Problem of Differential Equations. Acta Mathematica Academiae Scientiarum Hungarica, 7, 71-94. http://dx.doi.org/10.1007/BF02022967
- Guiliano, L. (1946) Generalazzioni di un lemma di Gronwall. Rend. Accad., Lincei, 1264-1271.
- Bellman, R. (1943) The Stability of Solutions of Linear Differential Equations. Duke Mathematical Journal, 10, 643- 647. http://dx.doi.org/10.1215/S0012-7094-43-01059-2
- Dragomir, S.S. and Kim, Y.H. (2002) On Certain New Integral Inequalities and Their Applications. JIPAM, 3, Article 65.
- Dragomir, S.S. and Kim, Y.H. (2003) Some Integral Inequalities for Functions of Two Variables. Electronic Journal of Differential Equations, 10, 1-13.
- Gronwall, T.H. (1919) Note on the Derivatives with Respect to a Parameter of Solutions of a System of Differential Equations. Annals of Mathematics, 20, 292-296. http://dx.doi.org/10.2307/1967124
- Nemyckii, V.V. and Stepanov, V.V. (1947) Qualitative Theory of Differential Equations. OGIZ, Moscow.







