Applied Mathematics
Vol.5 No.3(2014), Article ID:42812,11 pages DOI:10.4236/am.2014.53052
An Efficient Method to Solve Thermal Wave Equation
Department of Engineering Mathematics and Physics, Faculty of Engineering, Zagazig University, Zagazig, Egypt
Email: m_2010_salah@yahoo.com
Received November 22, 2013; revised December 22, 2013; accepted December 29, 2013
ABSTRACT
In this paper, an efficient technique of differential quadrature method and perturbation method is employed to analyze reaction-diffusion problems. An efficient method is presented to solve thermal wave propagation model in one and two dimensions. The proposed method marches in the time direction block by block and there are several time levels in each block. The global method of differential quadrature is applied in each block to discretize both the spatial and temporal derivatives. Furthermore, the proposed method is validated by comparing the obtained results with the available analytical ones and also compared with the hybrid technique of differential quadrature method and Runge-Kutta fourth order method.
Keywords:Reaction-Diffusion; Block Marching; Differential Quadrature; Perturbation
1. Introduction
Thermal wave is the reaction-diffusion equation which plays an ever-increasing role in the study of material parameters. It has been employed in optical investigations of solids, liquids, and gases with photo-acoustic and thermal lens spectroscopy. Thermal waves have also been used to analyze the thermal and thermodynamic properties of materials and for imaging thermal and material features within a solid sample [1].
In the past several decades, there has been greeting activity in developing numerical and analytical methods for the thermal wave equation. Due to the nonlinearity and complexity of such problems, only limited cases can analytically be solved [2-5]. Yan applied the projective Riccati equation method to solve Schrodinger equation in nonlinear optical fibers [2]. Then Mei, Zhang and Jiang employed the same method to get the exact solutions for some reaction-diffusion problems [3]. Abdusalam applied a factorization technique to find exact traveling wave solutions [4]. Chowdhury and Hashim obtain analytical solution for Cauchy reaction-diffusion problems using homotopy perturbation method [5]. Literature on the numerical solution of reaction-diffusion equations is sparse; singular perturbation method has been applied to solve reaction-diffusion equations by Puri et al. in [6]. David, Curtis and John introduced time integration methods to solve thermal wave propagation [7]. Marcus applied Finite difference method to study the dynamics of predator-prey interactions [8], and Chen et al. employed the finite element method to solve advective reaction-diffusion equations [9]. Then Christos et al. applied also the same method to solve the problem with boundary layers [10]. Meral and Sezgin used this method and finite difference method with a relaxation parameter to solve nonlinear reaction-diffusion equation in one and two dimensions [11]. Recently differential quadrature method has been efficiently employed in a variety of engineering problems [12]. Wu and Liu have introduced the generalization of the differential quadrature method to solve linear and non linear differential equations [13]. Moreover, Meral applied differential quadrature method and implicit Euler method to solve density dependent nonlinear reaction-diffusion equation [14]. Kajal applied differential quadrature and Runge-Kutta method to solve thermal wave, a blow-up and a Brusselator chemical dynamics system [15]. Kajal achieved high accuracy, but, there are some difficulties in the previous method that numerical solution is obtained layer by layer in the time direction so it can be expected that the accuracy of numerical solution is decreasing with time due to accumulation of numerical errors, also explicit scheme is used to update the solution using very small step size due to the limitation of stability condition. Also, Salah, Rania and Matbuly solved thermal wave equation in one and two dimensions using Implicit Euler and perturbation method. They compared the numerical solution with the results from Runge-Kutta method. They overcome the limitation of stability and one can use large step size [16]. Shu et al. early presented block-marching technique with DQ discretization to obtain the solution in the time direction block by block to overcome the above difficulty. Moreover, they used successive over-relaxation (SOR) iterative method to complete the solution achieving high accuracy and efficiency [17].
In this research block marching in time and DQ discretization in both the spatial and temporal derivatives are applied to obtain the solution in time direction block by block for thermal wave equation. In each block there are several time levels (layers). So the accumulation error is block by block instead of layer by layer. Perturbation method is used to complete the solution. The obtained results are compared with the previous analytical ones and also compared with the hybrid technique of differential quadrature method and Runge-Kutta fourth order method [15].
2. Numerical Procedure of Thermal Wave
The main strategy is to apply perturbation method of second order [18,19] then applying block-marching technique with DQ discretization to reduce the problem to a system of linear algebraic equations.
Propagation of thermal waves through a rectangular plate, is governed by [15]:
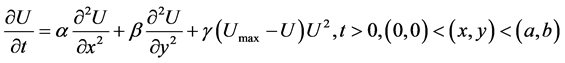 (1)
(1)
where:
U is a temperature,
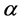 and
and  are diffusion parameters in direction of x and y, respectively.
are diffusion parameters in direction of x and y, respectively.
γ is reaction parameter.
a and b are plate dimensions in direction of x and y, respectively.
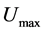 is a maximum temperature of the system.
is a maximum temperature of the system.
Along the external boundaries, the temperatures can be described as:
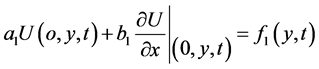 (2a)
(2a)
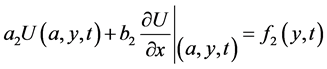 (2b)
(2b)
 (2c)
(2c)
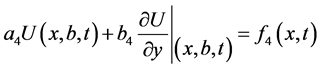 (2d)
(2d)
where 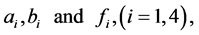 are known functions.
are known functions.
Then initial temperature may be described as:
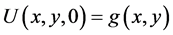 (3)
(3)
where 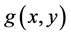 is a known function.
is a known function.
Solution of Equations (1)-(3) can be obtained as follows:
1) In the Kth block, the non uniform distribution is used Chebyshev-Gauss-Lobatto (CGL) in x, y and t directions respectively, such as [12]:
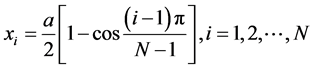 (4a)
(4a)
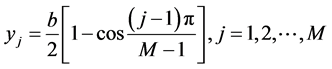 (4b)
(4b)
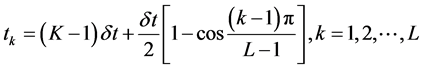 (4c)
(4c)
where N, M is the number of grid points in the x and y direction respectively, L is the number of time levels in the block and ![]() is the length of the block in time direction.
is the length of the block in time direction.
2) We can solve
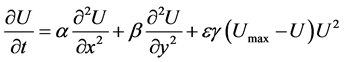 (5)
(5)
subjected to the prescribed to boundary and initial conditions in Equations (2) and (3), assuming
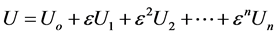 (6)
(6)
where  are unknowns functions and
are unknowns functions and 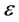 is a perturbation parameter.
is a perturbation parameter.
The following condition is tested to ensure the convergence condition [20] in previous series in Equation (6).
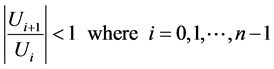 (7)
(7)
3) On sustainable substitution from Equation (6) into (5), one can reduce the problem to the following equation.
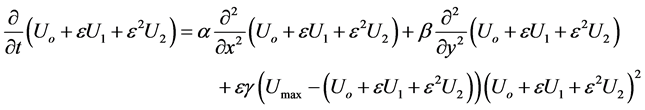 (8)
(8)
4) Applying zero order perturbation method such that,
 (9)
(9)
Subjected to boundary and initial conditions in Equations (2), (3), where block-marcing technique and differential quadrature method are used to reduce Equation (9) to a system of linear algebraic equations such that [12],
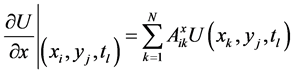 (10a)
(10a)
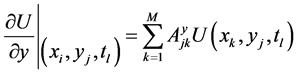 (10b)
(10b)
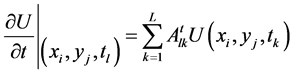 (10c)
(10c)
 (10d)
(10d)
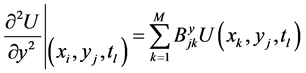 (10e)
(10e)
 (10f)
(10f)
where A and B are the first and second order weighting coefficients respectively.
By substitution of Equation (10) into Equation (9) result that,
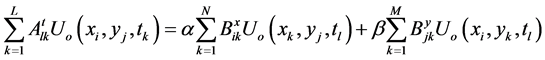 (11)
(11)
5) First order perturbation method is applied such that,
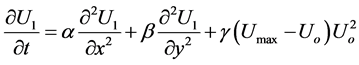 (12)
(12)
Subjected to the same boundary and initial conditions n Equations (2), (3), reduced to the following algebraic system
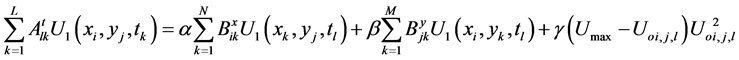 (13)
(13)
6) Also second order perturbation method is applied such that,
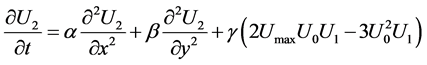 (14)
(14)
Subjected to the same boundary and initial conditions in Equations (2), (3), reduced to the following algebraic system
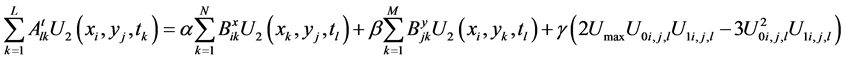 (15)
(15)
Finally, the series solution can be written as
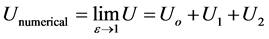 (16)
(16)
After obtaining the solution in the Kth block, we march to (K + 1)th block where the solution at the last time level at Kth block is considered an initial condition for (K + 1)th block. We carry on this process until the specified time is reached.
3. Results and Discussions
To ensure the accuracy of the proposed block marching technique, the thermal wave propagating model is solved using presented method and compared with the available analytical solution [15,21] and also compared with the hybrid technique of differential quadrature method and Runge-Kutta fourth order method [15].
3.1. Results for One Dimension Thermal Wave
Consider a one-dimensional problem of thermal wave propagation along x-direction as [16]:
 .
.
While
 (17)
(17)
The exact solution for such problem can be obtained as [21]:
 (18)
(18)
To validate the accuracy of numerical results, the following errors [16] are computed,
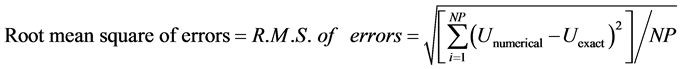 (19a)
(19a)
 (19b)
(19b)
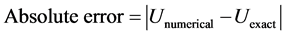 (19c)
(19c)
where P is the number of time steps in the case of using Runge-Kutta method and is considered the number of blocks multiplied by number of time levels in case of block marching technique.
For the numerical computation, the time domain is limited to ![]() and N = 7 while
and N = 7 while ![]() and L are not fixed. The efficiency of block marching technique is tested by CPU time required when the computation reaches to t = 20 s. Also convergence condition in Equation (7) is tested achieving higher accuracy at second order perturbation method as shown in Figure 1.
and L are not fixed. The efficiency of block marching technique is tested by CPU time required when the computation reaches to t = 20 s. Also convergence condition in Equation (7) is tested achieving higher accuracy at second order perturbation method as shown in Figure 1.
Table 1 shows R. M. S errors ˂ 7 × 10−6, R. S. S errors ˂ 2 × 10−4 and CPU time required is 0.132531 s.
The accuracy are very high at using δt = 0.5 and L = 4 so the number of blocks used in time interval ![]() are 40 blocks.
are 40 blocks.
From Table 2, we increase ![]() to 1.00 and time levels L to 10, the errors are approximately the same but CPU time is reduced slightly to 0.118479 s and we are used 20 blocks only.
to 1.00 and time levels L to 10, the errors are approximately the same but CPU time is reduced slightly to 0.118479 s and we are used 20 blocks only.
From Table 3, we increase δt to 2.00 and time levels L to 15, the accuracy of numerical results can be kept the same as the previous cases of δt = 0.5 and 1.00 but CPU time is increased to 0.129549 s as L is increased so
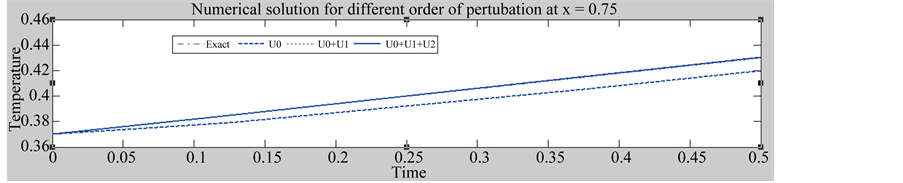
Figure 1. Satisfying convergence conditions.
Table 2. R.M.S, R.S.S errors, time steps and CPU times by present method for δt = 1.00 and L = 10.
Table 3. R.M.S, R.S.S errors, time steps and CPU times by present method for δt = 2.00 and L = 15.
the number of unknowns in each block for this case is much larger than previous cases shown in Tables 1 and 2. Furthermore, it can be shown from Table 4, when number of time levels fixed to 10 the accuracy kept the same as the previous cases but the efficiency is more improved as the CPU time reduced to 0.108360 s.
As well as, Figure 2 shows that at x = 0.25 and 0.75 the absolute error 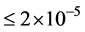 at different
at different ![]() and L.
and L.
Figure 3 shows that the effects of ![]() and L on the absolute error where
and L on the absolute error where ![]() is increasing the accuracy will increase and with proper choice of L will enhance also the efficiency. If δt is too large, the accuracy of numerical results can be greatly reduced if L is not large enough. In all previous cases the convergence condition in Equation (15) is satisfied.
is increasing the accuracy will increase and with proper choice of L will enhance also the efficiency. If δt is too large, the accuracy of numerical results can be greatly reduced if L is not large enough. In all previous cases the convergence condition in Equation (15) is satisfied.
To show the superiority of the block marching method, the RK4 method which is layer marching approach is also applied to solve the same problem. Two time step sizes of 0.001 and 0.005 are used for layer marching in the time direction. The numerical results of these two cases are listed respectively in Tables 5 and 6. From these two tables, it can be seen that RK4 method can achieve high accuracy at very small step size Dt = 0.001 with 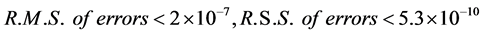 and at Dt = 0.005 with
and at Dt = 0.005 with  . Moreover, as shown in Figure 4, as Dt increased slightly to 0.00515 the stability condition will not achieved and the oscillation will occurs in the period
. Moreover, as shown in Figure 4, as Dt increased slightly to 0.00515 the stability condition will not achieved and the oscillation will occurs in the period![]() . On the other hand the efficiency is very small as the CPU time required to reach t = 20 s is much larger.
. On the other hand the efficiency is very small as the CPU time required to reach t = 20 s is much larger.
Figure 5 shows that the temperature distribution at different times and locations for numerical solution using block marching technique compared with exact solution and RK4 method.
3.2. Results for Two Dimensions Thermal Wave
Consider also a simple two dimensional problem with 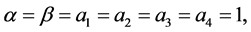
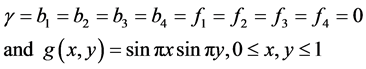 Which can be solved exactly as [22,23]:
Which can be solved exactly as [22,23]: .
.
The design of the numerical scheme is extended to two dimensions. Table 7 shows that for 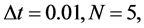
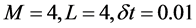 the obtained results agree with the analytical ones [21] with
the obtained results agree with the analytical ones [21] with 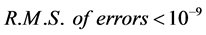 and the accuracy of block-marching is greater than the hybrid method.
and the accuracy of block-marching is greater than the hybrid method.
Figure 6 shows that absolute error for presented method < 0.005 while in hybrid method absolute error < 0.01, where also ensuring that accuracy of block-marching technique is better than hybrid method.
Figure 7 shows parametric study for the effect on block length and number of blocks, at t = 0.3 s we use one block each has length dt = 0.3, R.M.S error = 9.9012 × 10−6 and absolute error < 3 × 10−4 but if we decrease dt = 0.15 using two blocks, R.M.S error = 1.3382 × 10−4 and absolute error < 3 × 10−4, number of time levels doesn’t effect on the accuracy of solution.
4. Conclusions
The block marching technique with DQ discretization is employed to solve thermal wave propagations in one and two dimensions. The numerical results are obtained block by block in the time direction. Each block has several time levels. The length of the block in time direction ![]() and the number of time levels L can be adjusted to keep high accuracy and efficiency. The validity of the proposed technique is proved by comparing the obtained results with the previous analytical ones. The proposed technique needs a small number of grid points and a little com
and the number of time levels L can be adjusted to keep high accuracy and efficiency. The validity of the proposed technique is proved by comparing the obtained results with the previous analytical ones. The proposed technique needs a small number of grid points and a little com

Figure 2. Absolute error at different times and locations.
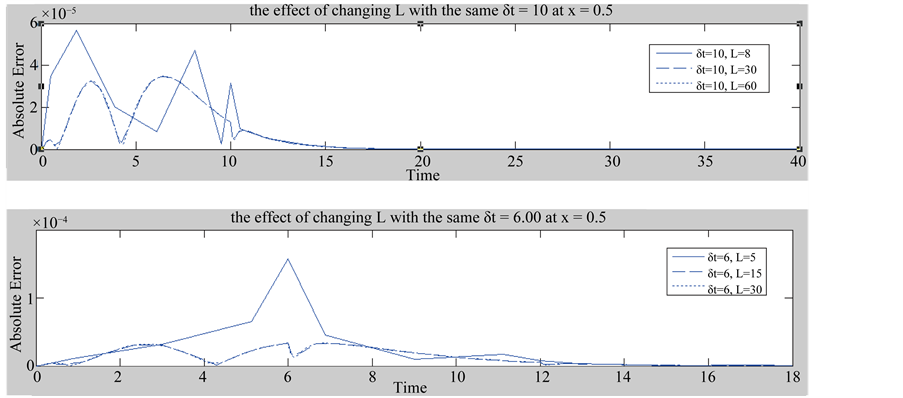
Figure 3. Behavior of absolute error with changing δt and L.
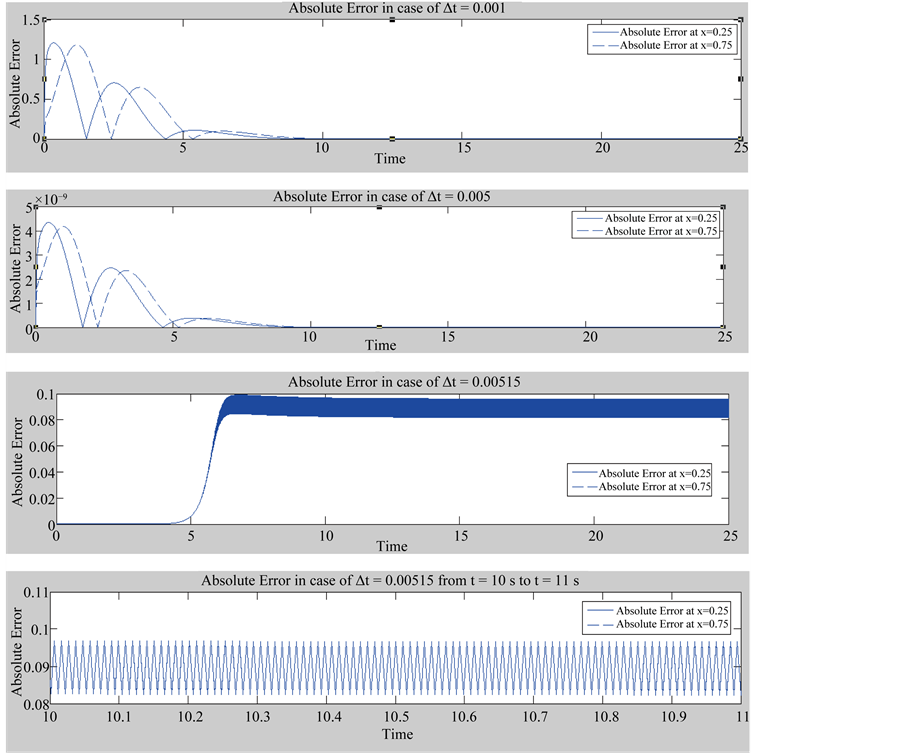
Figure 4. Absolute errors at different times and locations.
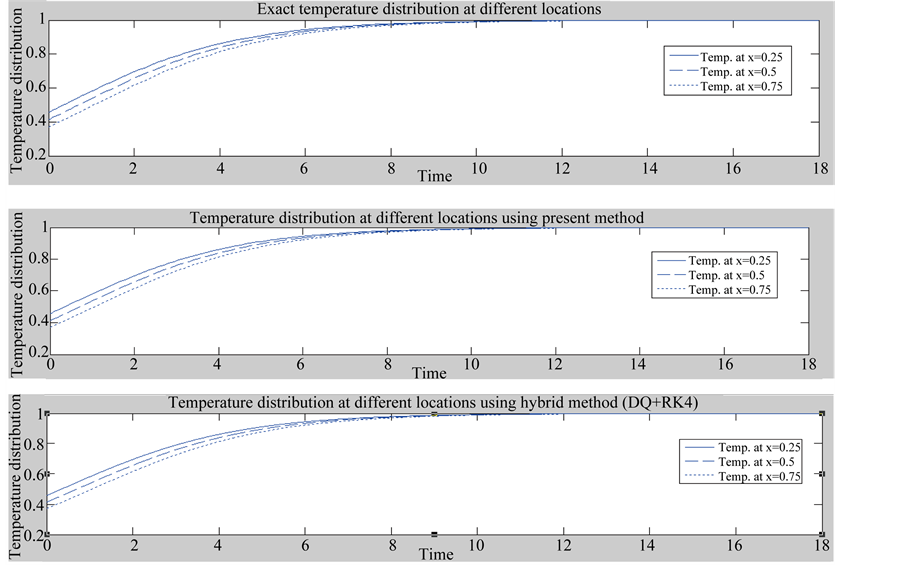
Figure 5. Temperature distributions at different times and locations.
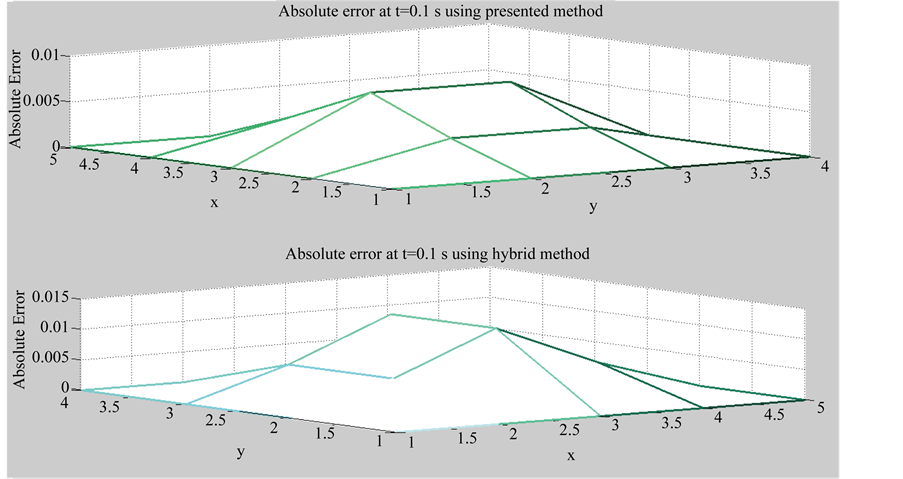
Figure 6. Absolute error at t = 0.1 s and different locations of x, y.
Table 7. Root mean square of errors for two dimensional thermal wave propagation at Δt = 0.01, N = 5, M = 4, L = 4, δt = 0.01.
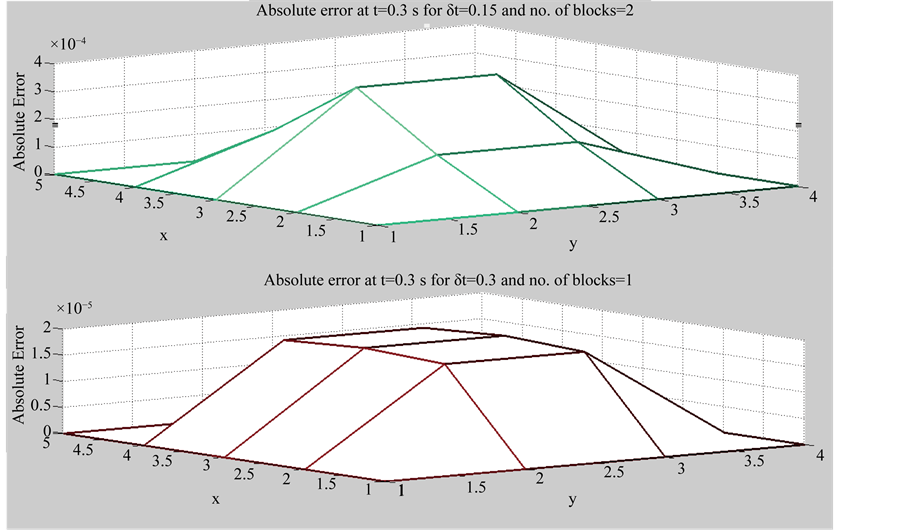
Figure 7. The effect of δt on absolute error.
putational effort to obtain accurate results with absolute error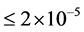 . Furthermore, the obtained results are also compared and agreed with the results of RK4 method.
. Furthermore, the obtained results are also compared and agreed with the results of RK4 method.
REFERENCES
- J. Opsal, A. Rosencwaig and D. L.Willenborg, “Thermal-Wave Detection and Thin-Film Thickness Measurements with Laser Beam Deflection,” Applied Optics, Vol. 22, No. 20, 1983, pp. 3169-3176. http://dx.doi.org/10.1364/AO.22.003169
- Z. Y. Yan, “Generalized Method and Its Application in the Higher-Order Nonlinear Schrodinger Equation in Nonlinear Optical Fibres,” Chaos Solitons and Fractals, Vol. 16, No. 5, 2003, pp. 759-766. http://dx.doi.org/10.1016/S0960-0779(02)00435-6
- J. Mei, H. Zhang and D. Jiang, “New Exact Solutions for a Reaction-Diffusion Equation and a Quasi-Camassa Holm Equation,” Applied Mathematics E-Notes, Vol. 4, 2004, pp. 85-91.
- E. S. Fahmy and H. A. Abdusalam, “Exact Solutions for Some Reaction Diffusion Systems with Nonlinear Reaction Polynomial Terms,” Applied Mathematical Sciences, Vol. 3, No. 11, 2009, pp. 533-540.
- M. S. H. Chowdhury and I. Hashim, “Analytical Solution for Cauchy Reaction-Diffusion Problems by Homotopy Perturbation Method,” Sains Malaysiana, Vol. 39, No. 3, 2010, pp. 495-504.
- S. Puri and K. Wiese, “Perturbative Linearization of Reaction-Diffusion Equations,” Journal of Physics A: Mathematical and General, Vol. 36, 2003, pp. 2043-2054. http://dx.doi.org/10.1088/0305-4470/36/8/303
- L. D. Ropp, N. J. Shadid and C. C. Ober, “Studies of the Accuracy of Time Integration Methods for Reaction-Diffusion Equations,” Journal of Computational Physics, Vol. 194, No. 2, 2004, pp. 544-574. http://dx.doi.org/10.1016/j.jcp.2003.08.033
- R. G. Marcus, “Finite-Difference Schemes for Reaction-Diffusion Equations Modeling Predator—Prey Interactions in MATLAB,” Bulletin of Mathematical Biology, Vol. 69, No. 3, 2007, pp. 931-956. http://dx.doi.org/10.1007/s11538-006-9062-3
- B. Liu, M. B. Allen, H. Kojouharov and B. Chen, “Finite-Element Solution of Reaction-Diffusion Equations with Advection,” Computational Mechanics, 1996, pp. 3-12.
- X. Christos and L. Oberbroeckling, “On the Finite Element Approximation of Systems of Reaction—Diffusion Equations by p/hp Methods,” Global Science, Vol. 28, No. 3, 2010, pp. 386-400.
- G. Meral and M. S. Tezer, “Solution of Nonlinear Reaction-Diffusion Equation by Using Dual Reciprocity Boundary Element Method with Finite Difference or Least Squares Method,” Advances in Boundary Element Techniques, 2008, pp. 317-22.
- C. Shu, “Differential Quadrature and Its Application in Engineering,” Springer Verlag, London, 2000. http://dx.doi.org/10.1007/978-1-4471-0407-0
- T. Y. Wu and G. R. Liu, “A Differential Quadrature as a Numerical Method to Solve Differential Equations,” Computational Mechanics, Vol. 24, No. 3, 1999, pp. 197-205. http://dx.doi.org/10.1007/s004660050452
- G. Meral, “Solution of Density Dependent Nonlinear Reaction-Diffusion Equation Using Differential Quadrature Method,” World Academy of Science, Engineering and Technology, Vol. 41, 2010, pp. 1178-1183.
- V. Kajal, “Numerical Solutions of Some Reaction-Diffusion Equations by Differential Quadrature Method,” International Journal of Applied Mathematics and Mechanics, Vol. 6, No. 14, 2010, pp. 68-80.
- M. Salah, R. M. Amer and M. S. Matbuly, “The Differential Quadrature Solution of Reaction-Diffusion Equation Using Explicit and Implicit Numerical Schemes,” Applied Mathematics, 2014.
- C. Shu, Q. Yao and K. S. Yeo, “Block-Marching in Time with DQ Discretization: An Efficient Method for Time-Dependent Problems,” Computer Methods in Applied Mechanics and Engineering, Vol. 191, No. 41, 2002, pp. 4587-4579. http://dx.doi.org/10.1016/S0045-7825(02)00387-0
- J. S. Nadjafi and A. Ghorbani, “He’s Homotopy Perturbation Method: An Effective Tool for Solving Nonlinear Integral and Integro-Differential Equations,” Computers and Mathematics with Applications, Vol. 58, No. 11-12, 2009, pp. 2379-2390. http://dx.doi.org/10.1016/j.camwa.2009.03.032
- H. S. Prasad and Y. N. Reddy, “Numerical Solution of Singularly Perturbed Differential-Difference Equations with Small Shifts of Mixed Type by Differential Quadrature Method,” American Journal of Computational and Applied Mathematics, Vol. 2, No. 1, 2012, pp. 46-52. http://dx.doi.org/10.5923/j.ajcam.20120201.09
- J. P. Hambleton and S. W. Sloan, “A Perturbation Method for Optimization of Rigid Block Mechanisms in the Kinematic Method of Limit Analysis,” Computers and Geotechnics, Vol. 48, 2013, pp. 260-271. http://dx.doi.org/10.1016/j.compgeo.2012.07.012
- M. Bastani and D. K. Salkuyeh, “A Highly Accurate Method to Solve Fisher’s Equation,” Indian Academy of Sciences, Vol. 78, No. 3, 2012, pp. 335-346.
- W. Y. Yang, W. Cao, T. Chung, J. Morris, et al., “Applied Numerical Methods Using Matlab,” John Wiley & Sons, Hoboken, New Jersey, 2005. http://dx.doi.org/10.1002/0471705195
- E. Kreyszig, “Advanced Engineering Mathematics,” John Wiley & Sons, Columbus, 2006.


