Applied Mathematics
Vol.4 No.4(2013), Article ID:30780,7 pages DOI:10.4236/am.2013.44101
A Note on the Guignard Constraint Qualification and the Guignard Regularity Condition in Vector Optimization
Faculty of Economics, University of Pavia, Via S. Felice, Pavia, Italy
Email: ggiorgi@eco.unipv.it
Copyright © 2013 Giorgio Giorgi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 12, 2012; revised February 14, 2013; accepted February 21, 2013
Keywords: Constraint Qualifications; Regularity Conditions; Optimality Conditions; Vector Optimization Problems
ABSTRACT
Some remarks are made on the use of the Abadie constraint qualification, the Guignard constraint qualifications and the Guignard regularity condition in obtaining weak and strong Kuhn-Tucker type optimality conditions in differentiable vector optimization problems.
1. Introduction
In discussing a gap between multiobjective optimization and scalar optimization (a gap first pointed out by Wang and Yang [1]), Aghezzaf and Hachimi [2] state that “in multiobjective optimization problems, many authors have derived the first-order and second-order necessary conditions under the Abadie constraint qualification, but never under the Guignard constraint qualification”. This deserves some comments. Indeed, some authors have proposed a suitable Guignard-Gould-Tolle constraint qualification (it would be better to speak of “GuignardGould-Tolle regularity condition”, as it involves also the objective function, besides the constraint functions) in order to obtain a Karush-Kuhn-Tucker type multiplier rule for a Pareto optimization problem.
For example, Maeda [3] considers the following Pareto optimization problem
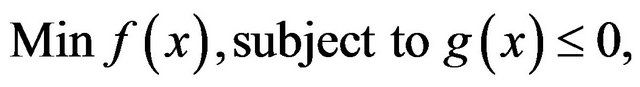
where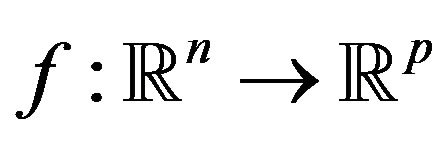 ,
, 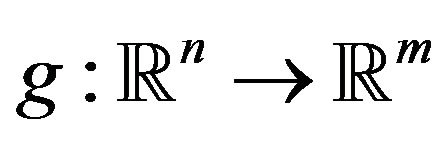 are differentiable functions, and introduces the following “generalized Guignard constraint qualification” for this problem
are differentiable functions, and introduces the following “generalized Guignard constraint qualification” for this problem
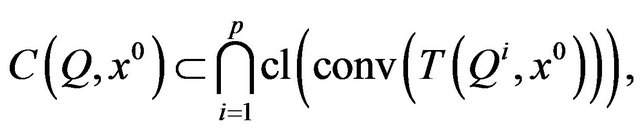
where 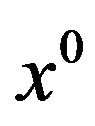 is a feasible vector,
is a feasible vector,
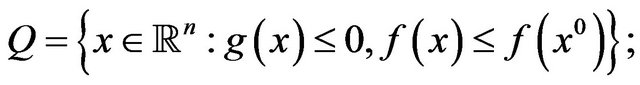
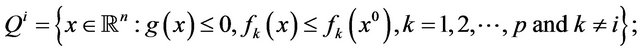
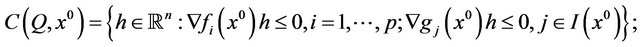
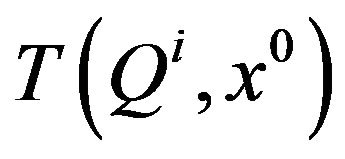 is the Bouligand tangent cone or contingent cone to
is the Bouligand tangent cone or contingent cone to 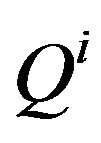 at
at 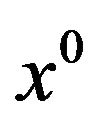 (see Definition 2) and
(see Definition 2) and  Indeed, in the above constraint qualification (better: regularity condition) the inclusion means in fact equality.
Indeed, in the above constraint qualification (better: regularity condition) the inclusion means in fact equality.
Jimenez and Novo [4], Giorgi, Jimenez and Novo [5], [6], Giorgi and Zuccotti [7] have given similar, but more general results. What is true is that the GuignardGould-Tolle theory cannot be transferred “sic et simpliciter” from the scalar to the vector case. Indeed, it is wellknown that if we have a scalar optimization problem
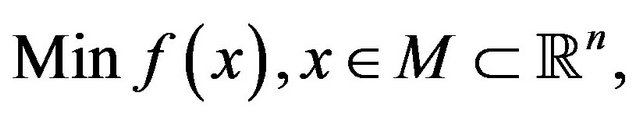
with , f differentiable, and
, f differentiable, and 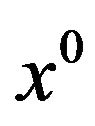 is a local solution of the said problem, then we have
is a local solution of the said problem, then we have
 (1)
(1)
(A* is the negative polar cone of the cone A). The result obtained by Guignard [8] seems at first sight more general, as Guignard claims that
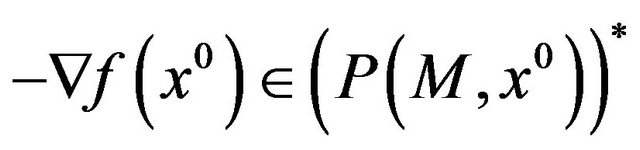
where 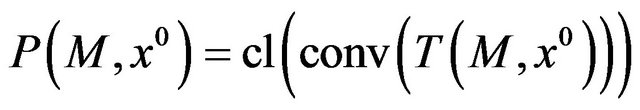 is the so-called pseudotangent cone to
is the so-called pseudotangent cone to  at
at . However, this greater generality is only apparent, as it is true that for any cone
. However, this greater generality is only apparent, as it is true that for any cone , it holds
, it holds
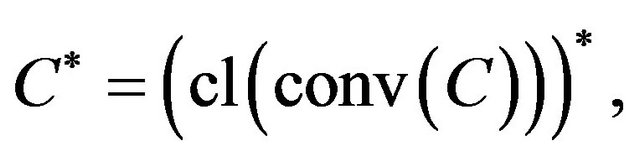
so we obtain

Relation (1) obviously is equivalent to the inconsistency of the inequality
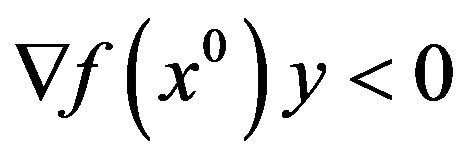
for  or, equivalently, for
or, equivalently, for 
Now, consider a vector optimization problem (vop)
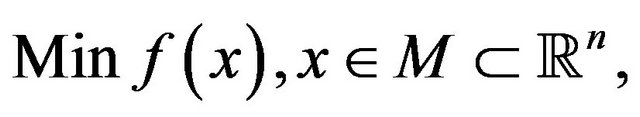
where 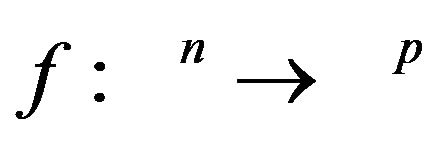 is differentiable. When, as in the present paper, the ordering cone is
is differentiable. When, as in the present paper, the ordering cone is 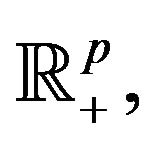 (vop) is also known as Pareto optimization problem. We recall some basic notions and definitions.
(vop) is also known as Pareto optimization problem. We recall some basic notions and definitions.
Definition 1.
A vector  is said to be a weak Pareto optimal point for (vop) if there does not exist another vector
is said to be a weak Pareto optimal point for (vop) if there does not exist another vector 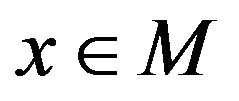 such that
such that 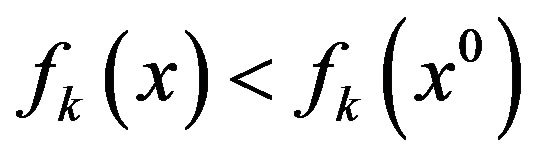 for all
for all 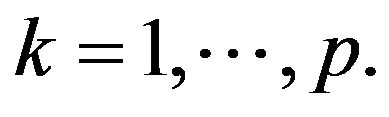 A vector
A vector 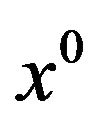 is said to be a Pareto optimal point for (vop) if there does not exist another vector
is said to be a Pareto optimal point for (vop) if there does not exist another vector 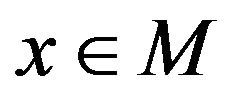 such that
such that 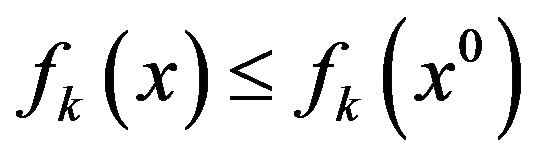 for all
for all 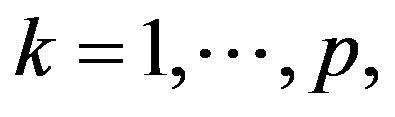 with
with 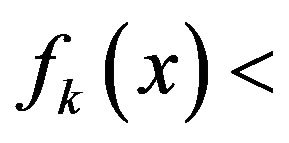
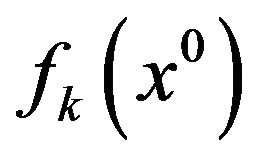 for at least one index. A vector
for at least one index. A vector 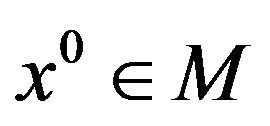 is a local weak Pareto optimal point (respectively, a local Pareto optimal point) if the above definitions hold with respect to
is a local weak Pareto optimal point (respectively, a local Pareto optimal point) if the above definitions hold with respect to 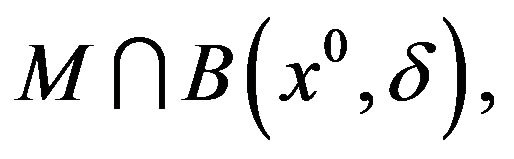 where
where 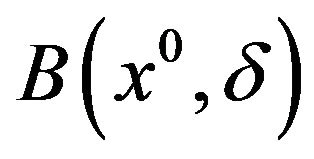 is a suitable neighborhood of
is a suitable neighborhood of 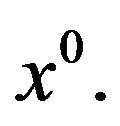
Definition 2.
Let 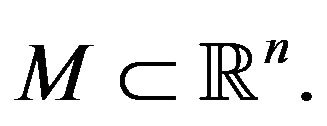 The contingent cone at
The contingent cone at 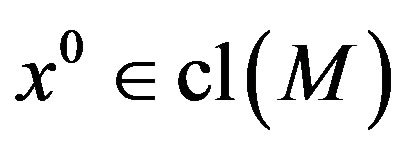 or Bouligand tangent cone at
or Bouligand tangent cone at 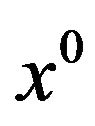 is:
is:
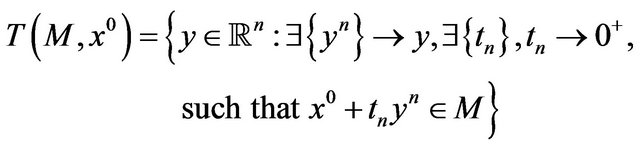
or, equivalently,

It is well-known that this cone is closed, but not necessarily convex (see, e.g., Aubin and Frankowska [9], Bazaraa and Shetty [10]).
It can be proved that if  is a local weak optimal point for (vop), then we have the relation (see, e.g., Bigi ([11], Corley [12], Giorgi and Zuccotti [13], Staib [14])
is a local weak optimal point for (vop), then we have the relation (see, e.g., Bigi ([11], Corley [12], Giorgi and Zuccotti [13], Staib [14])
 (2)
(2)
i.e. the system
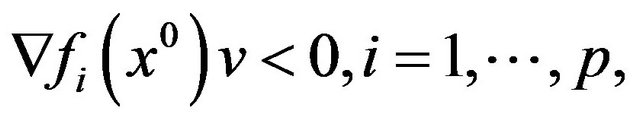 (3)
(3)
has no solution for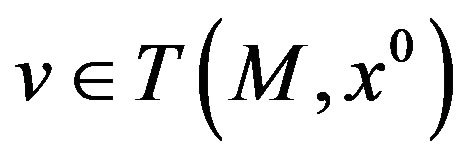 , i.e. it holds
, i.e. it holds
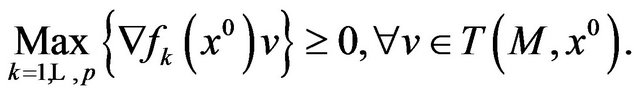
One may wonder if the system (3) (for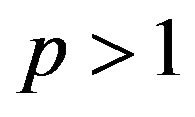 ) is also inconsistent for
) is also inconsistent for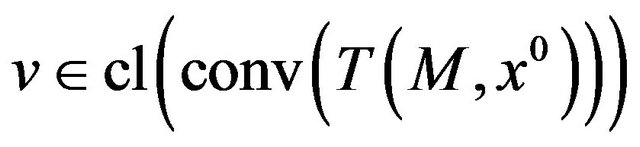 , as it holds for
, as it holds for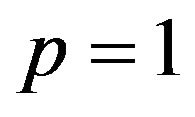 . The answer is: no, as shown by Wang and Yang [1] with a numerical example (a misprint in the example has been corrected by Castellani and Pappalardo [15]). This is the “gap”, with reference to a result of Guignard to which the title of the paper of Wang and Yang in its turn makes reference.
. The answer is: no, as shown by Wang and Yang [1] with a numerical example (a misprint in the example has been corrected by Castellani and Pappalardo [15]). This is the “gap”, with reference to a result of Guignard to which the title of the paper of Wang and Yang in its turn makes reference.
This note is organized as follows.
In Section 2 we give short proofs of the weak KuhnTucker type necessary optimality conditions, for a Pareto optimization problem with both inequality and equality constraints, under the Abadie constraint qualification, and of the strong Kuhn-Tucker type conditions, for the same problem, under a Guignard regularity condition.
In Section 3 we make some further comments on the said “gap” between scalar optimization problems and vector optimization problems.
The conclusions are briefly expounded in Section 4.
2. First Order Necessary Conditions: Abadie Constraint Qualification, Guignard Regularity Condition
The feasible set of (vop) is, from now on, specified by inequality and equality constraints. More precisely, we consider the problem
(vop)1 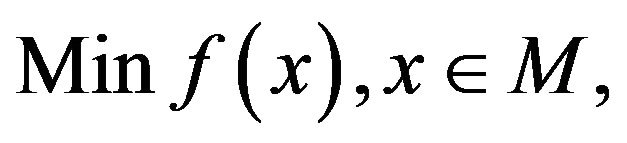
where

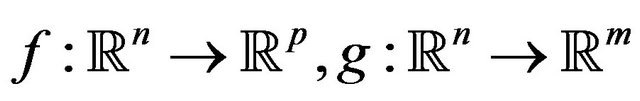 are differentiable at least in a neighborhood of the feasible point x0, and
are differentiable at least in a neighborhood of the feasible point x0, and  is continuously differentiable at least in the same neighborhood of x0. We denote by
is continuously differentiable at least in the same neighborhood of x0. We denote by 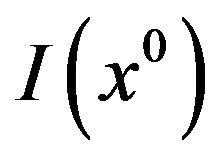 the index set of the active constraints
the index set of the active constraints 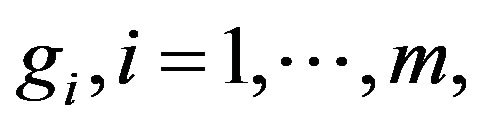 at
at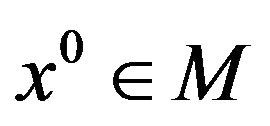 , i.e.
, i.e.
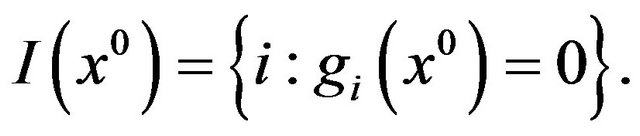
Let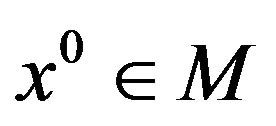 ; the cone
; the cone

is called the linearizing cone at  for (vop)1.
for (vop)1.
The cone
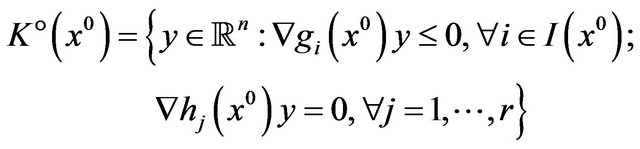
is called the weak linearizing cone at 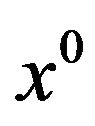 or cone of decreasing directions at
or cone of decreasing directions at 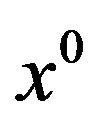 for (vop)1.
for (vop)1.
Lemma 1. (see Giorgi [16])
Let 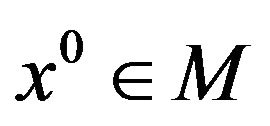 and let f, g and h verify the previous differentiability assumptions. Then we have:
and let f, g and h verify the previous differentiability assumptions. Then we have:
1) 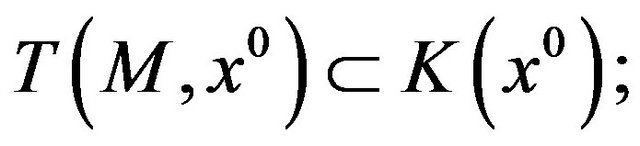
2) if the Jacobian matrix 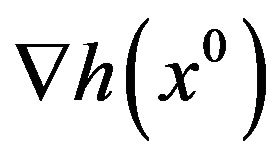 has full rank, it holds
has full rank, it holds 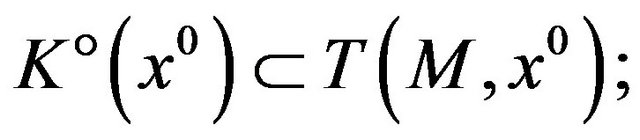
3) if, moreover, 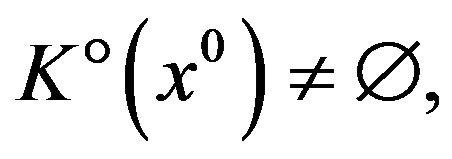 then it holds
then it holds
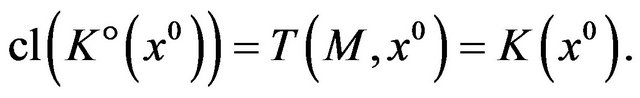
We are now ready to prove in a short way a Fritz John-type optimality condition for (vop)1.
Lemma 2.
Suppose that the Jacobian matrix 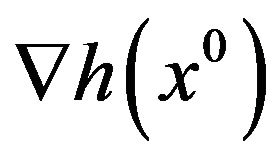 has full rank. Let
has full rank. Let 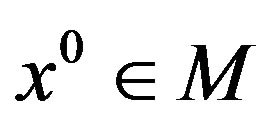 be a local weak Pareto optimal point for (vop)1. Then the system
be a local weak Pareto optimal point for (vop)1. Then the system
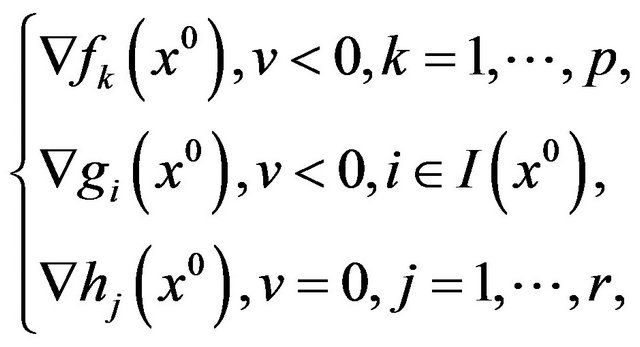 (4)
(4)
has no solution 
Proof.
Apply Lemma 1 to the optimality condition (3). 
Theorem 1.
If  is a local weak Pareto optimal point for (vop)1, then there exist vectors
is a local weak Pareto optimal point for (vop)1, then there exist vectors 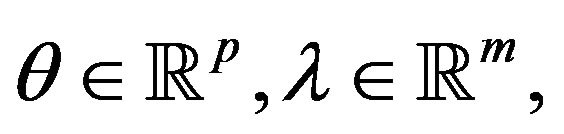 and
and 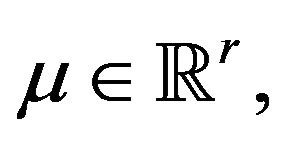 not all zero, such that
not all zero, such that
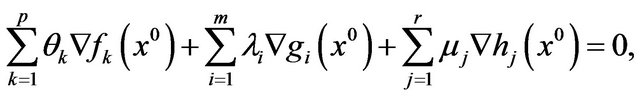 (5)
(5)
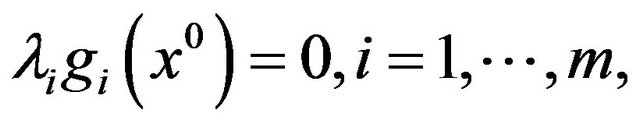 (6)
(6)
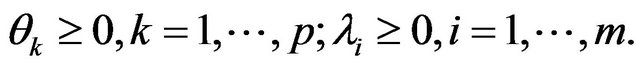 (7)
(7)
Proof.
If the gradients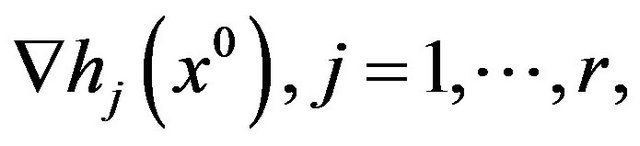 are linearly dependent, just set
are linearly dependent, just set 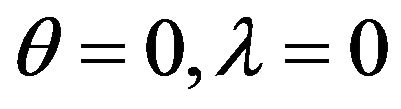 and choose a nonzero vector
and choose a nonzero vector 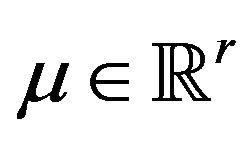 such that
such that
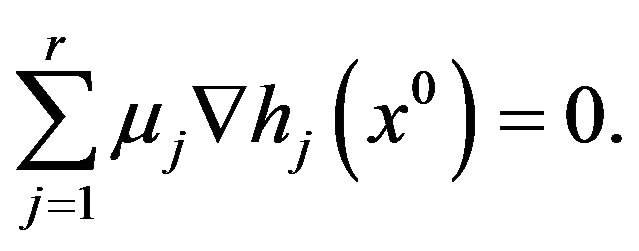
If the above gradients are linearly independent, the thesis follows from Lemma 2, applying the Motzkin alternative theorem (see, e. g., Mangasarian [17]) and setting 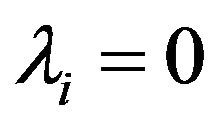 for all
for all 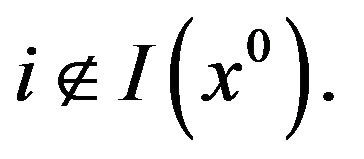

A Karush-Kuhn-Tucker-type optimality conditions for (vop)1, by means of the Abadie constraint qualification (acq), has been obtained by Lin [18] and by Singh [19]; however, their proofs work only if 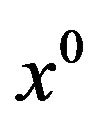 is a weak Pareto optimal point for (vop)1, and not a local weak Pareto optimal point. The flaw is corrected in Marusciac [20]; see also the errata corrige of Singh [19], who, however, does not justify his rectification; see also the paper of Wang [21], more specific on this point. We give here a simple proof of the result of Wang.
is a weak Pareto optimal point for (vop)1, and not a local weak Pareto optimal point. The flaw is corrected in Marusciac [20]; see also the errata corrige of Singh [19], who, however, does not justify his rectification; see also the paper of Wang [21], more specific on this point. We give here a simple proof of the result of Wang.
Definition 3.
The constraint set M satisfies the Abadie constraint qualification (acq) at  if
if
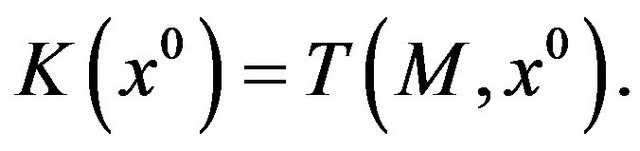
Due to relation 1) of Lemma 1, the (acq) can be written also as an inclusion
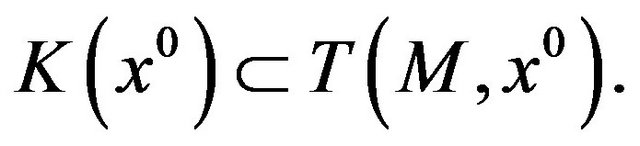
Singh [19] claims that his version, as an inclusion, of the (acq) is more general than the one proposed by Marusciac [20] as an equality.
Lemma 3.
Let 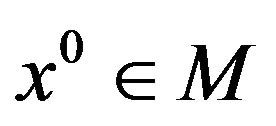 be a local weak Pareto optimal point for (vop)1, and suppose that the (acq) holds at
be a local weak Pareto optimal point for (vop)1, and suppose that the (acq) holds at . Then the system
. Then the system
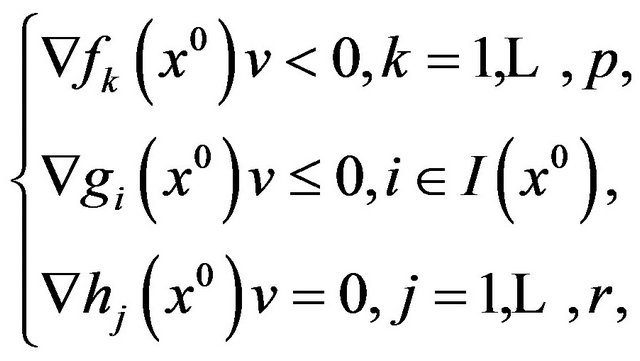 (8)
(8)
has no solution 
Proof.
Suppose, on the contrary, that the above system has a solution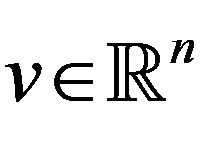 . Then, the (acq) implies that
. Then, the (acq) implies that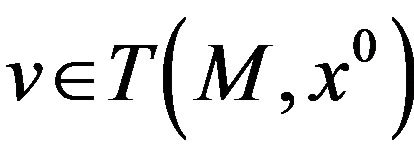 ; thanks to relation (3) it will hold
; thanks to relation (3) it will hold 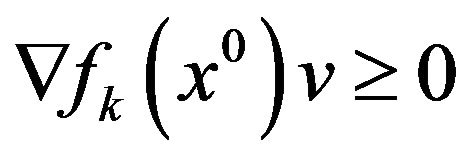 for at least one index k, contradicting the relations of the system.
for at least one index k, contradicting the relations of the system. 
Applying to system (8) the Motzkin theorem of the alternative, we get the following (weak) Karush-KuhnTucker-type multiplier rule for (vop)1.
Theorem 2.
Let  be a local weak Pareto optimal point for
be a local weak Pareto optimal point for  vop)1 and let the (acq) hold at
vop)1 and let the (acq) hold at . Then there exist vectors
. Then there exist vectors 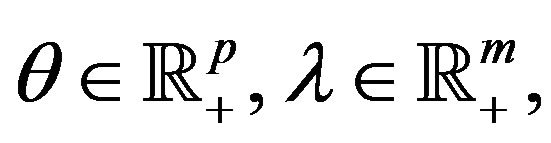 and
and , with
, with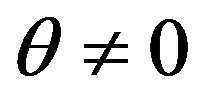 , such that (5), (6) and (7) hold.
, such that (5), (6) and (7) hold.
As the cone 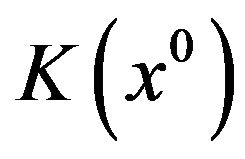 is polyhedric, the (acq) implies that
is polyhedric, the (acq) implies that 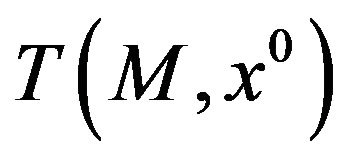 is a convex cone. If we substitute
is a convex cone. If we substitute 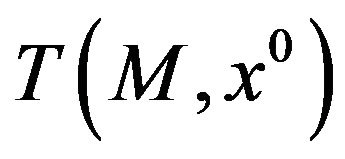 with the closure of its convex hull, we obtain the Guignard-Gould-Tolle constraint qualification (Guignard [8] Gould and Tolle [22])
with the closure of its convex hull, we obtain the Guignard-Gould-Tolle constraint qualification (Guignard [8] Gould and Tolle [22])
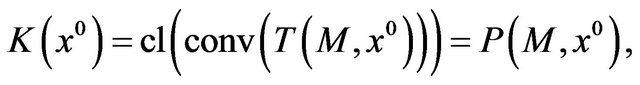 (9)
(9)
but, as already remarked in the Introduction, this more general constraint qualification does not enable to obtain, for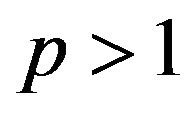 , the multiplier rule of Theorem 2, unless to make further assumptions on
, the multiplier rule of Theorem 2, unless to make further assumptions on 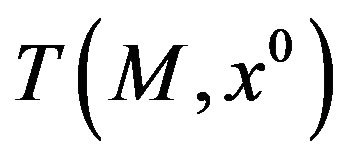 or on the objective function. See the next Section 3.
or on the objective function. See the next Section 3.
If we want to obtain a strong Karush-Kuhn-Tucker type optimality condition for (vop)1, i.e. a multiplier rule (5), (6) and (7), where 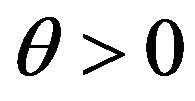 in (5), we have to impose some condition, where also the objective function is considered. We prefer, in this case, to speak of regularity conditions, instead of constraint qualifications. The condition considered by Maeda [3] and reported in the Introduction of the present paper, is therefore a regularity condition. For other regularity conditions for (vop)1 and their relationships, see also Jimenez and Novo [4] and Giorgi and Zuccotti [7].
in (5), we have to impose some condition, where also the objective function is considered. We prefer, in this case, to speak of regularity conditions, instead of constraint qualifications. The condition considered by Maeda [3] and reported in the Introduction of the present paper, is therefore a regularity condition. For other regularity conditions for (vop)1 and their relationships, see also Jimenez and Novo [4] and Giorgi and Zuccotti [7].
We now consider a slightly modified version of the Guignard regularity condition proposed by the above authors. See also Bigi [11].
Definition 4.
Let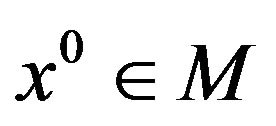 ; then the set
; then the set

is the cone of descent directions for f at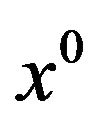 . Given any
. Given any , the set
, the set
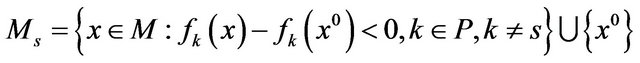
is the set of all feasible points, which do not allow  to be a weak minimum point for (vop)1 when the component
to be a weak minimum point for (vop)1 when the component 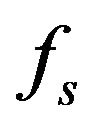 is dropped from f.
is dropped from f.
Definition 5.
Let 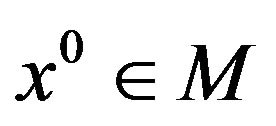 Then the (modified) Guignard-GouldTolle regularity condition (ggtrc) holds at
Then the (modified) Guignard-GouldTolle regularity condition (ggtrc) holds at 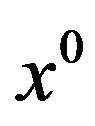 if
if
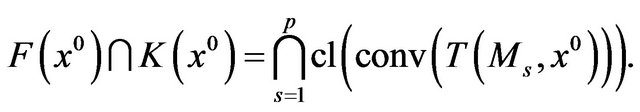
Lemma 4.
Suppose that 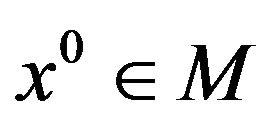 is a local weak Pareto optimal point for (vop)1 and that (ggtrc) holds at
is a local weak Pareto optimal point for (vop)1 and that (ggtrc) holds at  Then for each
Then for each 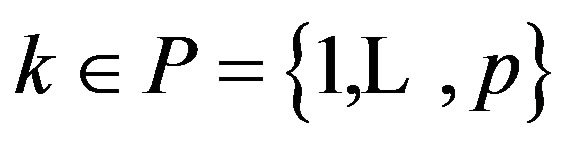 the following system
the following system
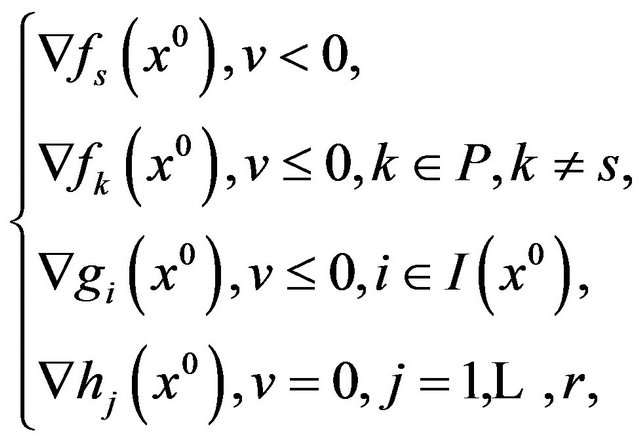 (10)
(10)
has no solution 
Proof.
On the contrary suppose that there exists 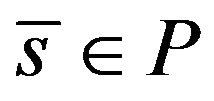 such that (10) has a solution. Therefore, (ggtrc) implies that
such that (10) has a solution. Therefore, (ggtrc) implies that 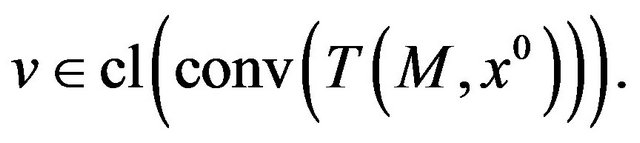 Since the definition of local weak Pareto optimal point for (vop)1 implies that
Since the definition of local weak Pareto optimal point for (vop)1 implies that  is a local minimum point of the scalar function
is a local minimum point of the scalar function 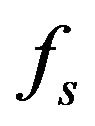 over
over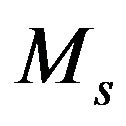 , then we get the inequality
, then we get the inequality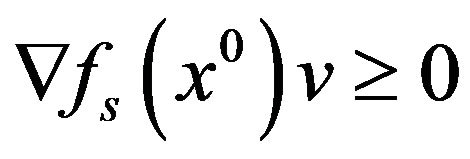 , in contradiction with the assumption.
, in contradiction with the assumption. 
The previous lemma, which states the impossibility of p systems, enables us to obtain a strong Karush-KuhnTucker-type multiplier rule for (vop)1.
Theorem 3.
Suppose that 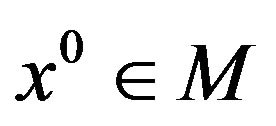 is a local weak Pareto optimal point for (vop)1 and that (ggtrc) holds at
is a local weak Pareto optimal point for (vop)1 and that (ggtrc) holds at 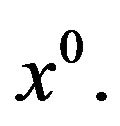 Then there exists vectors
Then there exists vectors 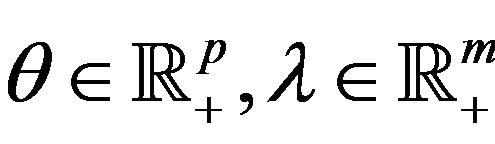 and
and  with
with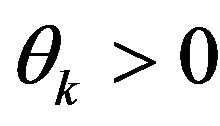 , for each
, for each 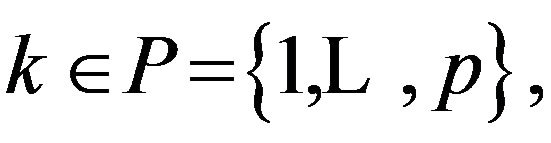 such that (5), (6) and (7) hold.
such that (5), (6) and (7) hold.
Proof.
The proof is immediate, by applying the Motzkin theorem of the alternative to system (10), for each 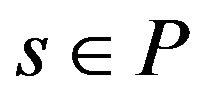 and summing up the resulting multipliers.
and summing up the resulting multipliers. 
We note that Maeda [3] has proposed a slightly weaker condition than (ggtrc), generalized to (vop)1 by Jimenez and Novo [4], by Giorgi, Jimenez and Novo [5,6], and by Giorgi and Zuccotti [7], but this weaker regularity condition “works” for local Pareto optimal points and not for the weak ones. Finally, we remark that (generalizing some approaches of Bigi and Pappalardo [23]) Maciel, Santos and Sottosanto [24] and Giorgi and Zuccotti [7] have studied the following question: which regularity condition for (vop)1 is both necessary and sufficient to obtain that , for all triplets of multipliers
, for all triplets of multipliers 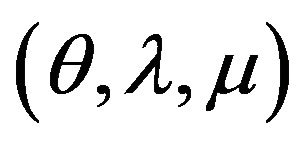 which satisfy relations (5), (6) and (7)? Let us denote by
which satisfy relations (5), (6) and (7)? Let us denote by 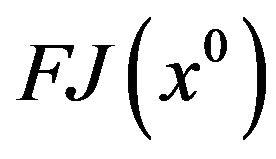 the above set of multipliers, i.e. the set of all Fritz John multipliers for (vop)1, and let us introduce the following generalization of the Mangasarian-Fromovitz constraint qualification.
the above set of multipliers, i.e. the set of all Fritz John multipliers for (vop)1, and let us introduce the following generalization of the Mangasarian-Fromovitz constraint qualification.
Definition 6.
Let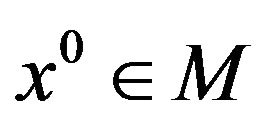 , then the Mangasarian-Fromovitz regularity condition (mfrc) for (vop)1 is satisfied at
, then the Mangasarian-Fromovitz regularity condition (mfrc) for (vop)1 is satisfied at 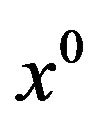 if:
if:
1) the vectors  are linearly independent;
are linearly independent;
2) for all  the system
the system
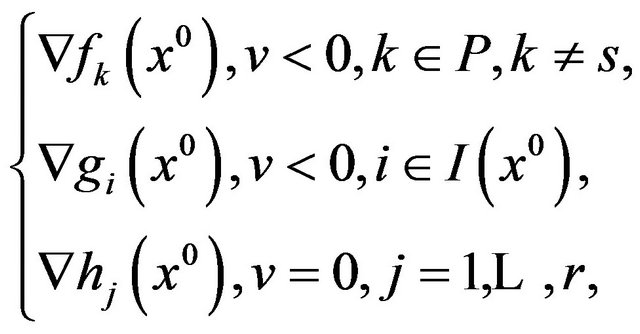
has solution 
It can be proved the following result (see Maciel, Santos and Sottosanto [24], Giorgi and Zuccotti [7]).
Theorem 4.
Let  and let
and let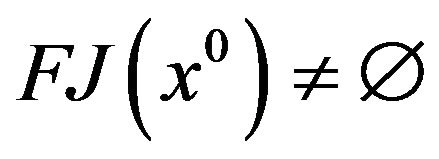 . Then in (vop)1 we have
. Then in (vop)1 we have 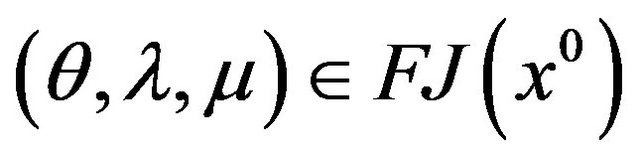 with
with 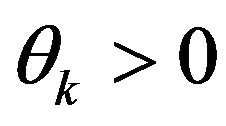 for all
for all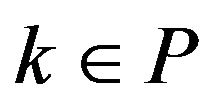 , if and only if (mfrc) holds at
, if and only if (mfrc) holds at 
In this section we have given a simple and short proof of the Fritz John type and of the weak Kuhn-Tucker type necessary optimality conditions for the problem (vop)1, under the Abadie constraint qualification. This completes and improves what previously proved by Singh [19]. We give also a short proof of the strong Kuhn-Tucker type conditions for (vop)1, under a Guignard regularity condition. This improves what previously proved by Maeda [3].
3. Again on the “Gap” between Scalar Problems and Vector Problems
We have described in the Introduction the “gap” occurring between scalar and vector optimization problems, generated by the use of the classical Guignard-GouldTolle constraint qualification. We have also mentioned this “gap” in the previous section. An obvious sufficient condition to remove this “gap” is that the cone 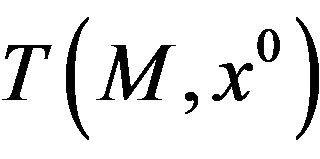 is convex; this condition has been envisaged by Wang and Yang [1], who, however, did not go further in the discussion. It is well-known that
is convex; this condition has been envisaged by Wang and Yang [1], who, however, did not go further in the discussion. It is well-known that 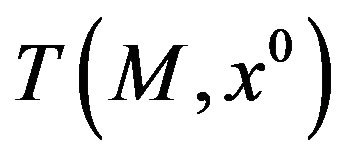 is convex when M is a convex set. As the structure of the contingent cone
is convex when M is a convex set. As the structure of the contingent cone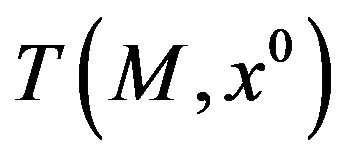 , as of all the other first-order local cone approximations, depends only from the structure of M arouund
, as of all the other first-order local cone approximations, depends only from the structure of M arouund 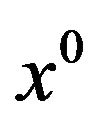 (see, e.g., Elster and Thierfelder [25]), we can state that
(see, e.g., Elster and Thierfelder [25]), we can state that 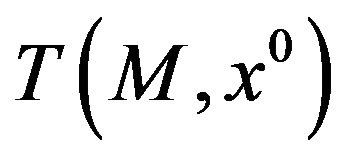 is convex also when M is locally convex at
is convex also when M is locally convex at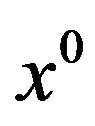 , i.e. there exists a neighborhood of
, i.e. there exists a neighborhood of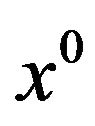 ,
, 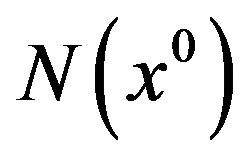 , such that
, such that 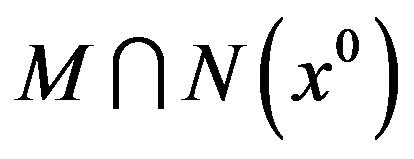 is a convex set. This is no longer true when M is only star-shaped at
is a convex set. This is no longer true when M is only star-shaped at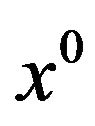 , i.e.
, i.e. 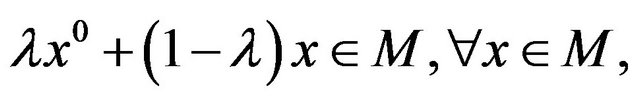 contrary to what stated in Giorgi and Guerraggio [26] and to what seems stated in Palata [27] and in Staib [14].
contrary to what stated in Giorgi and Guerraggio [26] and to what seems stated in Palata [27] and in Staib [14].
If M is star-shaped at 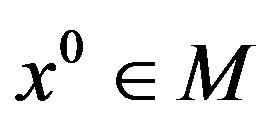 it holds that
it holds that 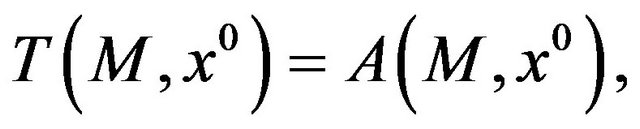 where
where
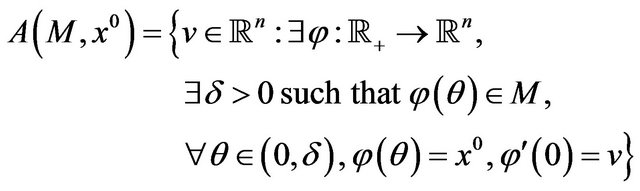
is the cone of the attainable directions or Kuhn-Tucker cone at 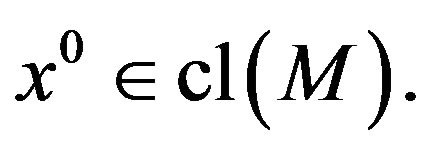 So, when
So, when  is star-shaped at
is star-shaped at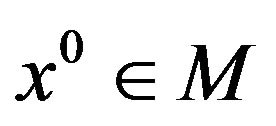 , the (acq) and the Kuhn-Tucker constraint qualification (ktcq)
, the (acq) and the Kuhn-Tucker constraint qualification (ktcq)
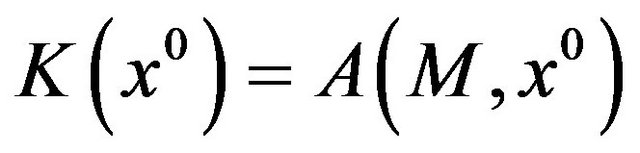
coincide (see Bazaraa and Shetty [10], who, however, do not recognize that the cone 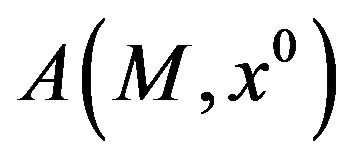 is closed).
is closed).
It is also well-known that if 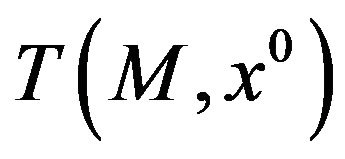 equals the Clarke tangent cone
equals the Clarke tangent cone
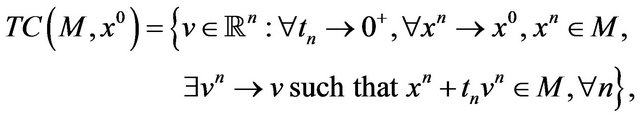
then 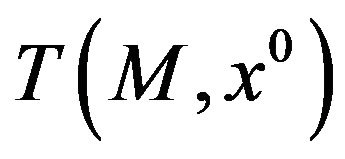 is convex, being
is convex, being 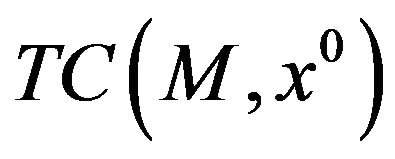 always closed and convex. In this case Penot [28] qualifies the set M as tangentially regular at
always closed and convex. In this case Penot [28] qualifies the set M as tangentially regular at  We follow the treatment of Aubin and Frankowska [9].
We follow the treatment of Aubin and Frankowska [9].
Definition 7.
We say that a closed subset  is sleek at
is sleek at 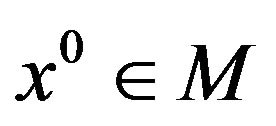 if the multivalued map
if the multivalued map 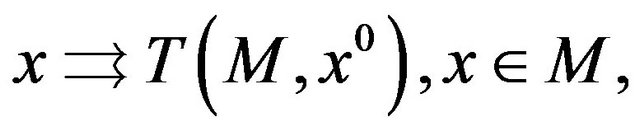 is lower semicontinuous at
is lower semicontinuous at .
.
Theorem 5. (Aubin and Frankowska [9])
Let M be a closed subset of 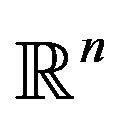 and
and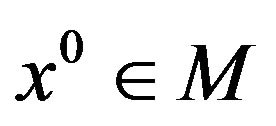 . If
. If  is sleek at
is sleek at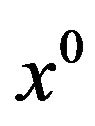 , then the contingent cone
, then the contingent cone  and the Clarke tangent cone
and the Clarke tangent cone 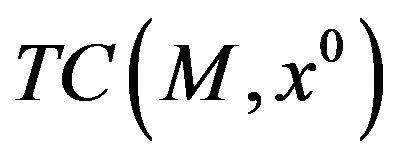 coincide and consequently
coincide and consequently 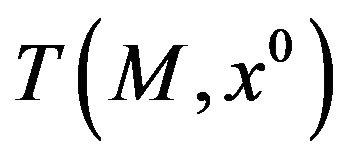 is convex.
is convex.
Another possibility to remove the “gap” is suggested by Castellani and Pappalardo [15], who impose that the objective function f is convexlike ad refer a result of Li and Wang [29]. This can be proved directly in the following way.
Definition 8.
A function 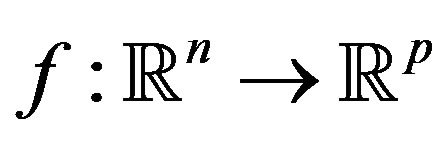 is convexlike on the nonempty set
is convexlike on the nonempty set 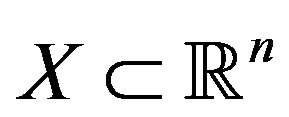 if for any
if for any  and any
and any 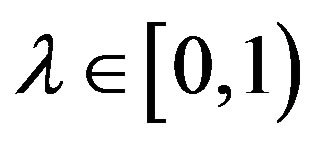 there exists
there exists 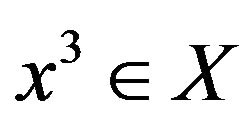 such that
such that
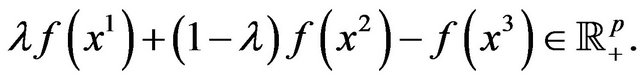
Note that in the above definition 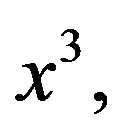 which usually depends from
which usually depends from 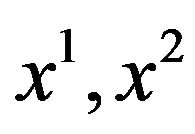 and
and 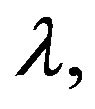 is not required to be the convex combination of
is not required to be the convex combination of 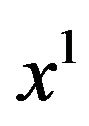 and
and 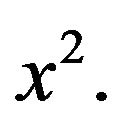 Note, moreover, that if
Note, moreover, that if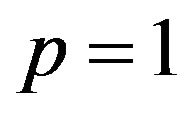 , then any real-valued function is convexlike. Obviously, all convex functions
, then any real-valued function is convexlike. Obviously, all convex functions 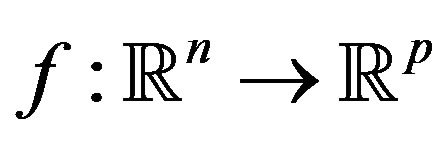 are convexlike; this is only a sufficient condition. For other sufficient conditions see Elster and Nehse [30]. See also Hayashi and Komiya [31] and Jeyakumar [32] for applications of convexlike functions to optimization problems.
are convexlike; this is only a sufficient condition. For other sufficient conditions see Elster and Nehse [30]. See also Hayashi and Komiya [31] and Jeyakumar [32] for applications of convexlike functions to optimization problems.
A straightforward consequence of Definition 8 is the following characterization.
Theorem 6.
The function 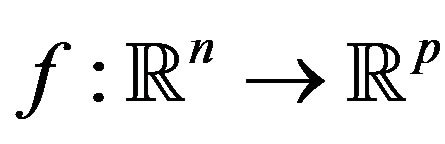 is convexlike on
is convexlike on 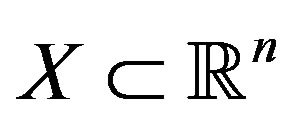 if and only if the set
if and only if the set 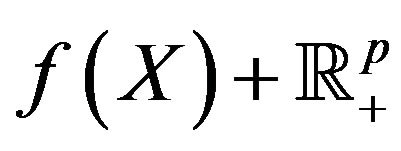 is convex.
is convex.
Theorem 7.
Suppose that f is convexlike on  If
If 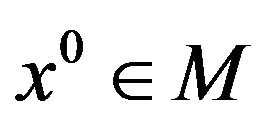 is a weak Pareto optimal point for (vop), then there exists a nonnegative nonzero vector
is a weak Pareto optimal point for (vop), then there exists a nonnegative nonzero vector 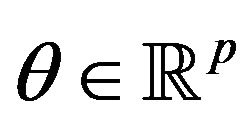 such that
such that  is a minimum point of the scalar problem
is a minimum point of the scalar problem
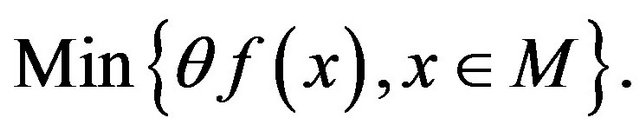
Proof.
By assumption  The convexlikeness assumption on f implies that
The convexlikeness assumption on f implies that 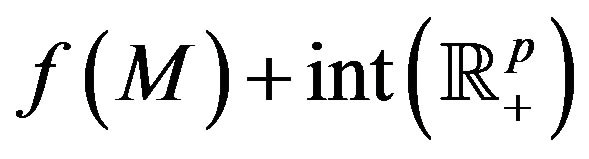 is convex; therefore the usual separation theorem implies the existence of a nonzero vector
is convex; therefore the usual separation theorem implies the existence of a nonzero vector 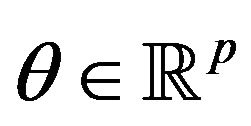 and of a scalar
and of a scalar 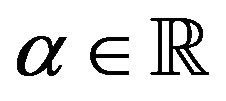 such that
such that
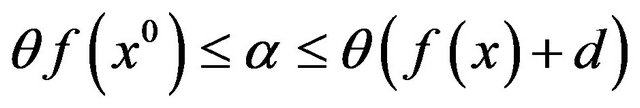
for all  and for all
and for all 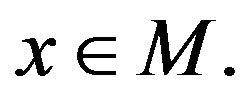 Therefore, considering
Therefore, considering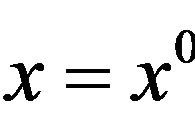 , we obtain
, we obtain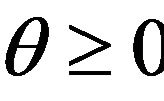 ; given any
; given any 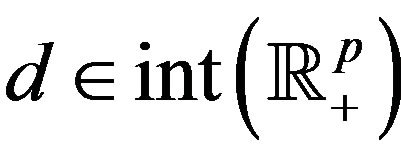
and considering td as 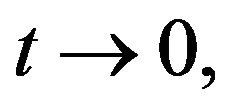 we get
we get 
and therefore the thesis follows. 
We note that in the proof of the above ressult we use the property that 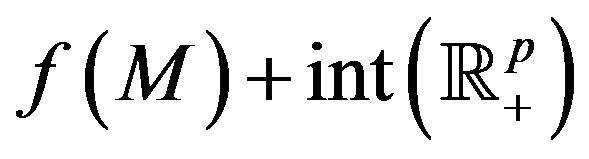 is a convex set; this weaker condition is equivalent that
is a convex set; this weaker condition is equivalent that 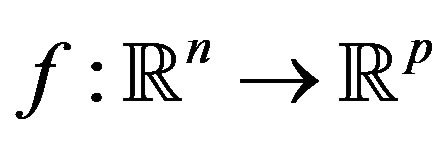 is subconvexlike on M (see Li and Wang [29]). The “scalarization theorem” just proved allows us to state the following result (recall that for
is subconvexlike on M (see Li and Wang [29]). The “scalarization theorem” just proved allows us to state the following result (recall that for 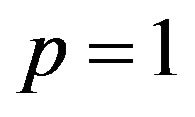 the Guignard-GouldTolle theory is consistent).
the Guignard-GouldTolle theory is consistent).
Theorem 8.
Suppose that 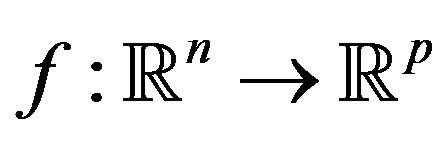 is convexlike (or subconvexlike) on M. If
is convexlike (or subconvexlike) on M. If 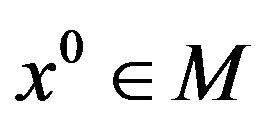 is a weak Pareto optimal point for (vop), then
is a weak Pareto optimal point for (vop), then
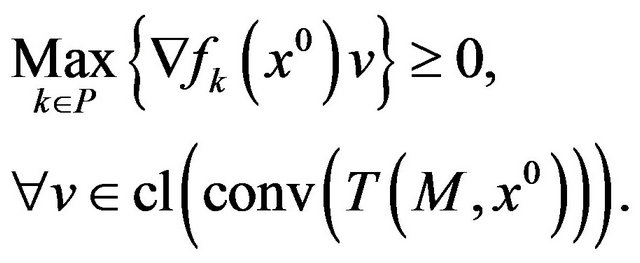
Similarly, with reference to (vop)1, we can assert the following result.
Theorem 9.
Suppose that 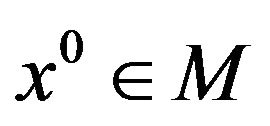 is a weak Pareto optimal point for (vop)1 and that
is a weak Pareto optimal point for (vop)1 and that 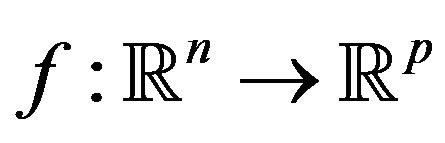 is convexlike (or subconvexlike) on M. Suppose that the Guignard-GouldTolle constraint qualification (9) holds at
is convexlike (or subconvexlike) on M. Suppose that the Guignard-GouldTolle constraint qualification (9) holds at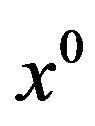 . Then, there exist multipliers
. Then, there exist multipliers 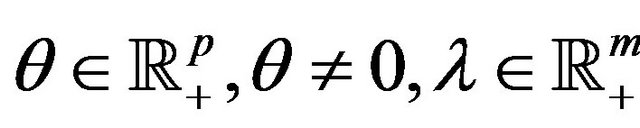 and
and  such that (5), (6) and (7) hold.
such that (5), (6) and (7) hold.
Another condition which allows to apply to (vop)1 the (ggtcq) and which entails the objective function f is given in the following theorem.
Theorem 10.
Let 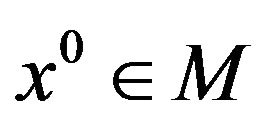 be a weak Pareto optimal point for (vop)1; suppose that x0 verifies the (ggtcq) and that there exists a nonnegative vector
be a weak Pareto optimal point for (vop)1; suppose that x0 verifies the (ggtcq) and that there exists a nonnegative vector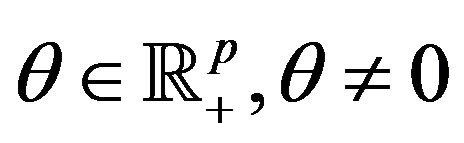 , such that
, such that
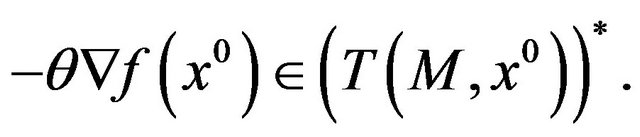
Then  verifies the conditions (5), (6) and (7).
verifies the conditions (5), (6) and (7).
Proof.
The (ggtcq) can be equivalently written in the form
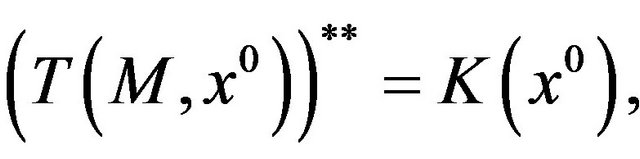 or
or  On the other hand, being
On the other hand, being 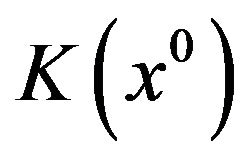 a polyhedral cone, determined by the vectors
a polyhedral cone, determined by the vectors ,
, 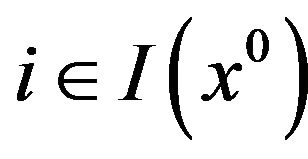 and
and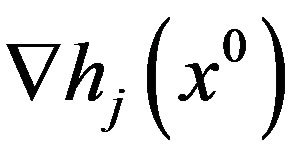 ,
, 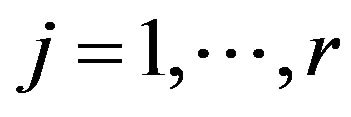 , its polar will be given by
, its polar will be given by
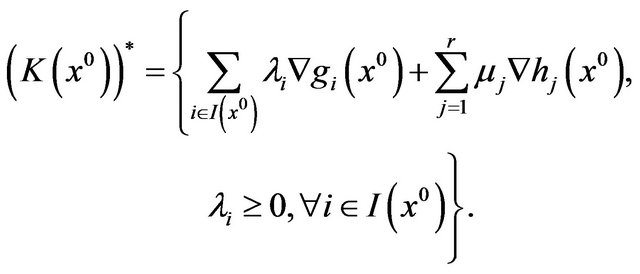
Therefore, being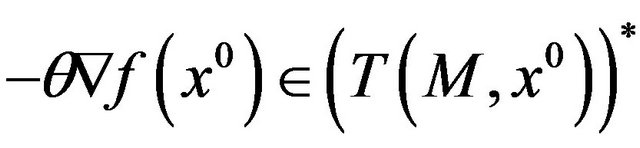 , we can write
, we can write

i.e. the conditions (5), (6) and (7), by choosing 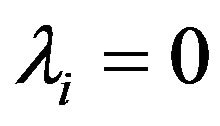 for
for 

We remark that if  is a weak Pareto opyimal point for (vop)1, then, for each convex cone S, with
is a weak Pareto opyimal point for (vop)1, then, for each convex cone S, with , there exists a nonnegative vector
, there exists a nonnegative vector ,
, 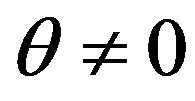 , such that
, such that , The proof is left to the reader (apply the classical theorem on separation of convex sets). Note that when
, The proof is left to the reader (apply the classical theorem on separation of convex sets). Note that when 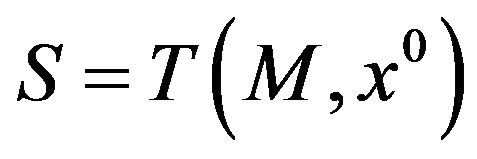 we obtain the result already observed at the beginning of this Section and obtain also the result stated in the previous theorem.
we obtain the result already observed at the beginning of this Section and obtain also the result stated in the previous theorem.
In this section we have investigated the reasons for the existence of a gap between a scalar programming problem and a multiobjective programming problem (vop)1, gap which has its origins in the use of the classical Guignard-Gould-Tolle constraint qualification. We have given some proposals to remove the said gap.
4. Conclusions
The aim of the present paper is twofold. On one side we present simple and brief optimality conditions of the Fritz John type and of the Kuhn-Tucker type (both weak and strong) for a Pareto multiobjective programming problem with both inequality and equality constraints. On the other side we investigate the existence of a gap, originated by the use of the classical Guignard constraint qualification, between a scalar nonlinear programming problem and the Pareto problem described above.
The author thanks an anonymous referee for his suggestions.
REFERENCES
- S. Y. Wang and F. M. Yang, “A Gap between Multiobjective Optimization and Scalar Optimization,” Journal of Optimization Theory and Applications, Vol. 68, No. 2, 1991, pp. 389-391. doi:10.1007/BF00941577
- B. Aghezzaf and M. Hachimi, “On a Gap between Multiobjective Optimization and Scalar Optimization,” Journal of Optimization Theory and Applications, Vol. 109, No. 2, 2001, pp. 431-435. doi:10.1023/A:1017574608034
- T. Maeda, “Constraint Qualifications in Multiobjective Optimization Problems: Differentiable Case,” Journal of Optimization Theory and Applications, Vol. 80, No. 3, 1994, pp. 483-500. doi:10.1007/BF02207776
- B. Jimenez and V. Novo, “Cualificaciones de Restricciones en Problemas de Optimización Vectorial Diferenciables,” XVI CEDYA Congreso de Ecuaciones Diferenciales y Aplicaciones, VI CMA Congreso de Matemática Aplicada, Vol. 1, 1999, pp. 727-734.
- G. Giorgi, B. Jimenez and V. Novo, “On Constraint Qualifications in Directionally Differentiable Multiobjective Optimization Problems,” RAIRO—Operations Research, Vol. 38, No. 3, 2004, pp. 255-274. doi:10.1051/ro:2004023
- G. Giorgi, B. Jimenez and V. Novo, “Strong KuhnTucker Conditions and Constraint Qualifications in Locally Lipschitz Multiobjective Optimization,” TOP, Vol. 17, No. 2, 2009, pp. 288-304. doi:10.1007/s11750-008-0058-z
- G. Giorgi and C. Zuccotti, “Again on Regularity Conditions in Differentiable Vector Optimization,” Annals of the University of Bucharest (Mathematical Series), Vol. LX, No.2, 2011, pp. 157-177.
- M. Guignard, “Generalized Kuhn-Tucker Conditions for Mathematical Programming Problems in a Banach Space,” SIAM Journal on Control, Vol. 7, No. 2, 1969, pp. 232- 241. doi:10.1137/0307016
- J. P. Aubin and H. Frankowska, “Set-Valued Analysis,” Birkhäuser, Boston, 1990.
- M. S. Bazaraa and C. M. Shetty, “Foundations of Optimization,” Springer Verlag, Berlin, 1976. doi:10.1007/978-3-642-48294-6
- G. Bigi, “Optimality and Lagrangian Regularity in Vector Optimization,” Ph.D. Thesis, University of Pisa, Pisa, 1999.
- H. W. Corley, “On Optimality Conditions for Maximizations with Respect to Cones,” Journal of Optimization Theory and Applications, Vol. 46, No. 1, 1985, pp. 67-78. doi:10.1007/BF00938760
- G. Giorgi and C. Zuccotti, “On the Use of Some Tangent Cones and Sets in Vector Optimization,” Report N. 169, Università di Pavia, Pavia, 2012.
- T. Staib, “On Necessary and Sufficient Optimality Conditions for Multicriteria Optimization Problems,” ZORMethods and Models of Operations Research, Vol. 35, 1991, pp. 231-248.
- M. Castellani and M. Pappalardo, “About a Gap between Multiobjective Optimization and Scalar Optimization,” Journal of Optimization Theory and Applications, Vol. 109, No. 2, 2001, pp. 437-439. doi:10.1023/A:1017526724872
- G. Giorgi, “Remarks on the Fritz John Conditions for Problems with Inequality and Equality Constraints,” International Journal of Pure and Applied Mathematics, Vol. 71, 2011, pp. 643-657.
- O. L. Mangasarian, “Nonlinear Programming,” McGrawHill, New York, 1969.
- J. G. Lin, “Maximal Vectors and Multi—Objective Optimization,” Journal of Optimization Theory and Applications, Vol. 18, No. 1, 1976, pp. 41-64. doi:10.1007/BF00933793
- C. Singh, “Optimality Conditions in Multiobjective Differentaible Programming,” Journal of Optimization Theory and Applications, Vol. 53, No. 1, 1987, pp. 115-123. C. Singh, “Errata Corrige,” Journal of Optimization Theory and Applications, Vol. 57, No. 2, 1988, p. 369. doi:10.1007/BF00938547
- I. Marusciac, “On Fritz John Type Optimality Criterion in Multiobjective Optimization,” L’Analyse Numérique et la Théorie de l’Approximation, Vol. 11, 1982, pp. 109-114.
- S. Y. Wang, “A Note on Optimality Conditions in Multiobjective Programming,” Systems Science and Mathematical Sciences, Vol. 1, 1988, pp. 184-190.
- F. J. Gould and J. W. Tolle, “A Necessary and Sufficient Qualification for Constrained Optimization,” SIAM Journal on Applied Mathematics, Vol. 20, No. 2, 1971, pp. 164-172. doi:10.1137/0120021
- G. Bigi and M. Pappalardo, “Regularity Conditions in Vector Optimization,” Journal of Optimization Theory and Applications, Vol. 102, No. 1, 1999, pp. 83-96. doi:10.1023/A:1021890328184
- M. C. Maciel, S. A. Santos and G. N. Sottosanto, “Regularity Conditions in Differentiable Vector Optimization Revisited,” Journal of Optimization Theory and Applications, Vol. 142, No. 2, 2009, pp. 385-398. doi:10.1007/s10957-009-9519-2
- K. H. Elster and J. Thierfelder, “Abstract Cone Approximations and Generalized Differentiability in Nonsmooth Optimization,” Optimization, Vol. 19, No. 3, 1988, pp. 315-341. doi:10.1080/02331938808843348
- G. Giorgi and A. Guerraggio, “On the Notion of Tangent Cone in Mathematical Programming,” Optimization, Vol. 25, No. 1, 1992, pp. 11-23. doi:10.1080/02331939208843804
- J. Palata, “A Survey of Conical Approximations Used in Optimization,” Optimization, Vol. 20, No. 2, 1989, pp. 147-161. doi:10.1080/02331938908843424
- J. P. Penot, “A Characterization of Tangential Regularity,” Nonlinear Analysis, Methods & Applications, Vol. 5, No. 6, 1981, pp. 625-643. doi:10.1016/0362-546X(81)90079-1
- Z. F. Li and S. Y. Wang, “Lagrange Multipliers and Saddle Points in Multiobjective Programming,” Journal of Optimization Theory and Applications, Vol. 83, No. 1, 1994, pp. 63-81. doi:10.1007/BF02191762
- K. H. Elster and R. Nehse, “Optimality Conditions for Some Nonconvex Problems,” Lecture Notes in Control and Information Sciences, Vol. 23, Springer Verlag, Berlin, 1980, pp. 1-9.
- M. Hayashi and K. Komiya, “Perfect Duality for Convexlike Programs,” Journal of Optimization Theory and Applications, Vol. 38, No. 2, 1982, pp. 179-189. doi:10.1007/BF00934081
- V. Jeyakumar, “Convexlike Alternative Theorems and Mathematical Programming,” Journal of Optimization Theory and Applications, Vol. 16, No. 5, 1985, pp. 643- 652. doi:10.1080/02331938508843061

