ABSTRACT

The aim of this paper is to study the existence of integrable solutions of a nonlinear functional integral equation in the space of Lebesgue integrable functions on unbounded interval, L₁(R₊). As an application we deduce the existence of solution of an initial value problem of fractional order that be studied only on a bounded interval. The main tools used are Schauder fixed point theorem, measure of weak noncompactness, superposition operator and fractional calculus.

1. Introduction

The class of functional integral equations of various types plays very important role in numerous mathematical research areas. An interesting feature of functional integral equations is its role in the study of many problems of functional differential Equations [1-4].

In this work we study the solvability of the following initial value problem

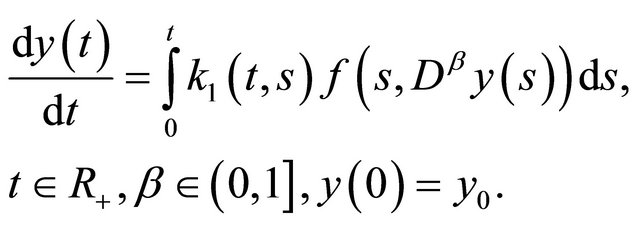(1)

where 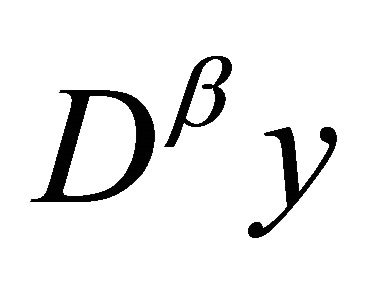denotes the fractional derivative of order of with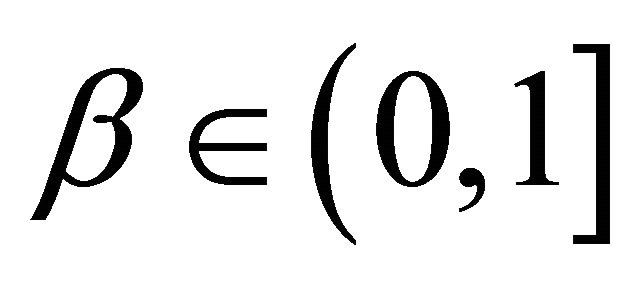. Such initial value problem of arbitrary order (1) was investigated in [5-7]. To achieve this goal, let us consider the integral equation

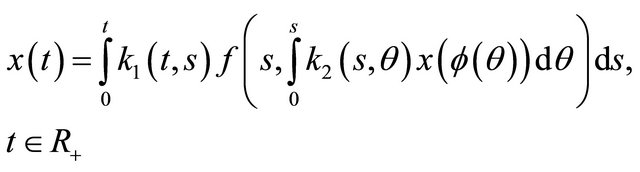(2)

which is different from that studied in [2].

Section 2 contains some basic results. Our main result will be given in Section 3. Solvability of the considered initial value problem will be discussed in Section 4.

2. Basic Concepts

This section is devoted to recall some notations and known results that will be needed in the sequel.

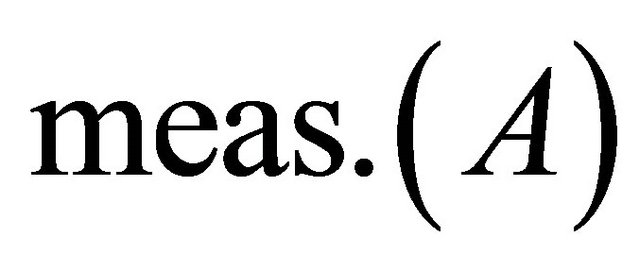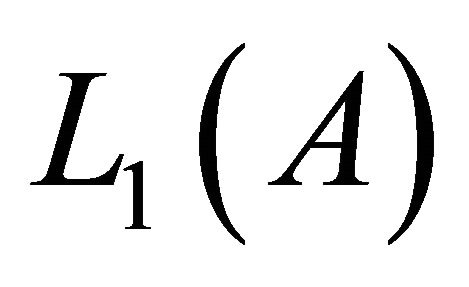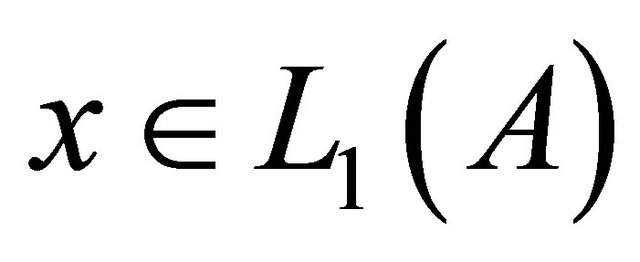If is a Lebesgue measurable subset of the set of real numbers then we use the symbol to denote the Lebesgue measure of. Let be the space of all real functions defined and Lebesgue measurable on the set. If then the norm of 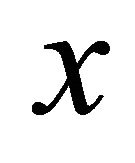is defined as:

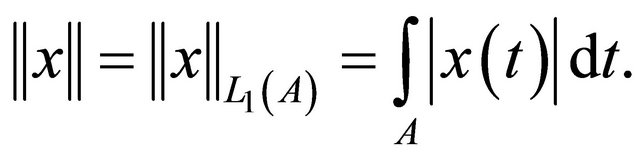
when 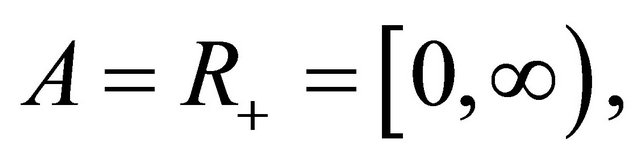we will write 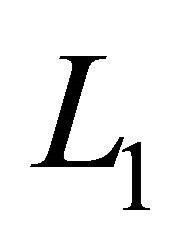instead of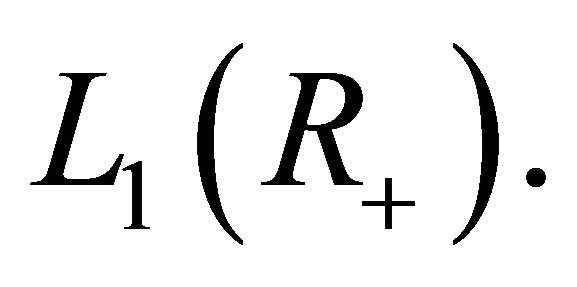

2.1. The Superposition Operator

An important operator called the superposition operator can be investigated in the theories of differential integral and functional equations [4,8-10]. It can be defined as follows:

Definition 1. Assume that satisfies Carathéodory conditions, that is it is measurable in for any 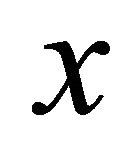and continuous in 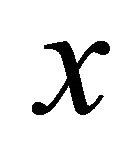for almost all where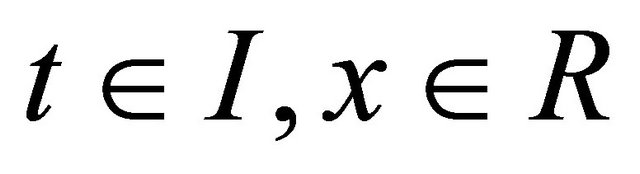. Then for every measurable function 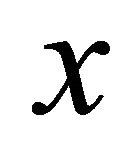on the interval we assign the function:

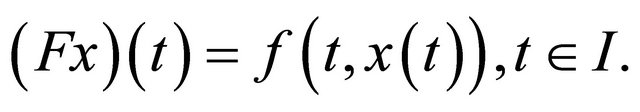
The operator F defined in this way is called the superposition operator generated by the function.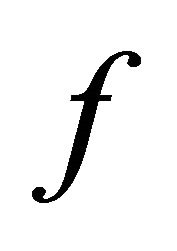

Carathéodory [11] gave the first contribution to the theory of the superposition operator and proved its measurability according to the measurability of.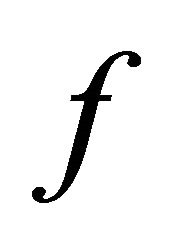

We state the following result giving the necessary and sufficient condition so that the superposition operator generated by will map continuously into itself [12].

Theorem 2. Let 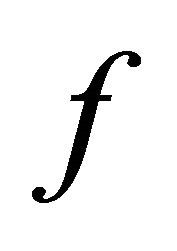satisfy the conditions in Definition 1. The superposition operator generated by the function 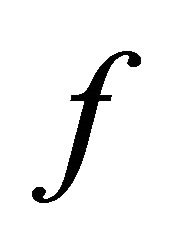maps continuously the space into itself if and only if:

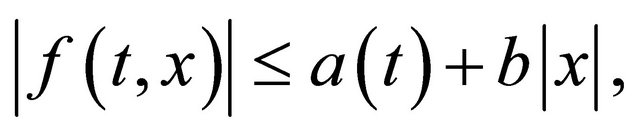
for all 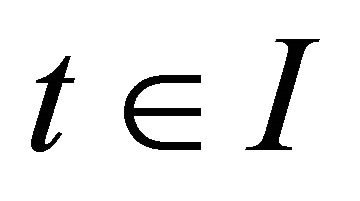and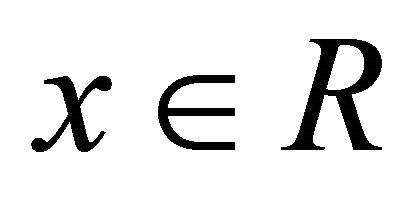, where is a function that belongs to 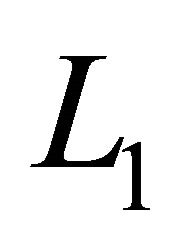and is a nonnegative constant.

It is known that a real valued continuous function is measurable and that the converse is not necessarily true. However, for the converse we have the following results due to Dragoni [13].

Theorem 3. Let be a bounded interval and 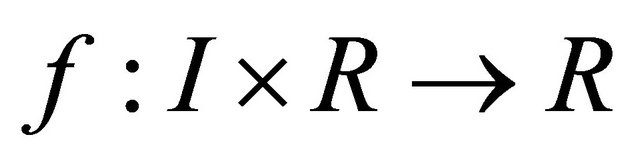be a function satisfying Caratheodory conditions. Then for each 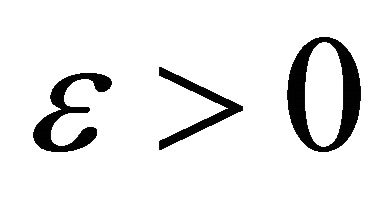there exists a closed subset 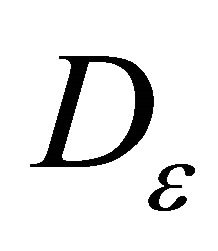of the interval I such that 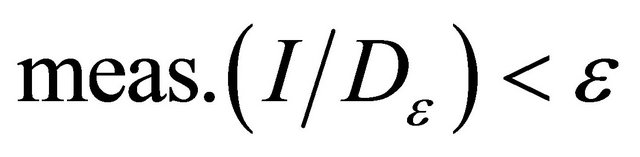and 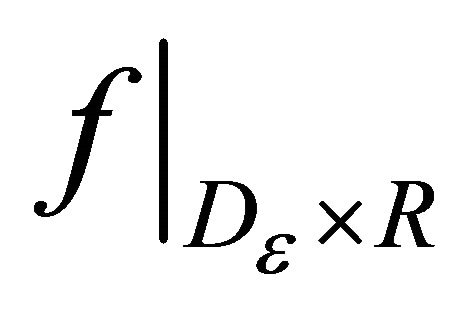is continuous.

2.2. Volterra Integral Operator

We proceed by recalling some basic facts concerning the linear Volterra integral operator in the Lebesgue space 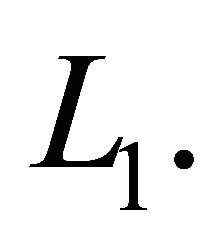Suppose is a given function which is measurable with respect to both variables where

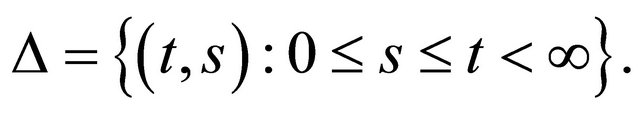
For an arbitrary function 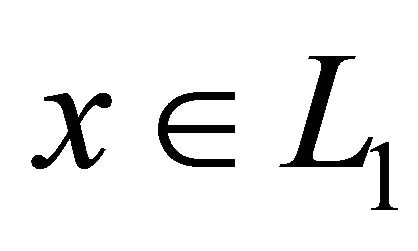define Volterra integral operator as follows:

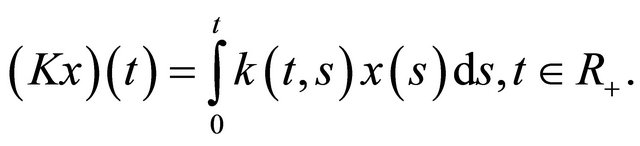
It is well known that if then it is continuous [4,9].

In general, it is rather difficult to find necessary and sufficient conditions for the function 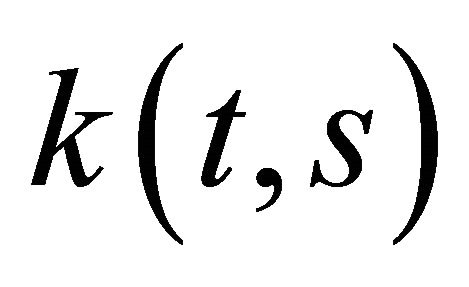guaranteeing that the integral operator transforms the space into itself. Some special cases of this problem were discussed in [4,14]. In this direction we state the next result [15]:

Theorem 4. Let 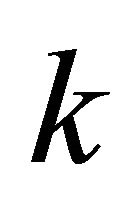be measurable on and such that

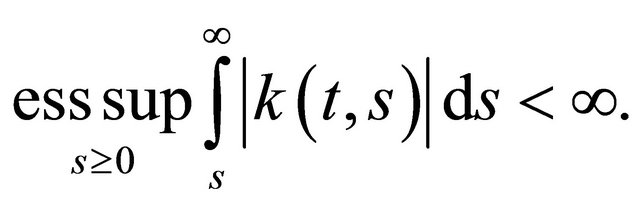
Then the Volterra integral operator generated by 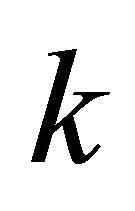maps (continuously) the space 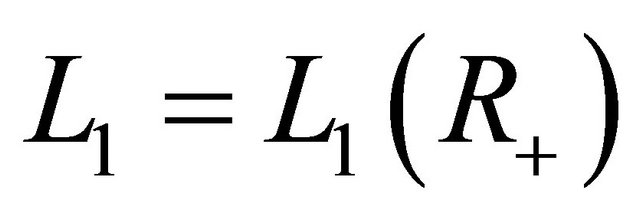into itself and the norm of this operator is majorized by the number

.

Observe that if 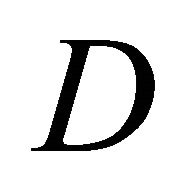is a nonempty and measurable subset of 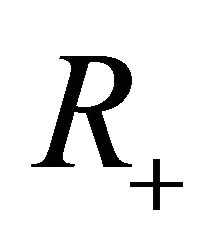then we can also consider the linear Volterra integral operator associated with the Lebesgue space

NamelyIf 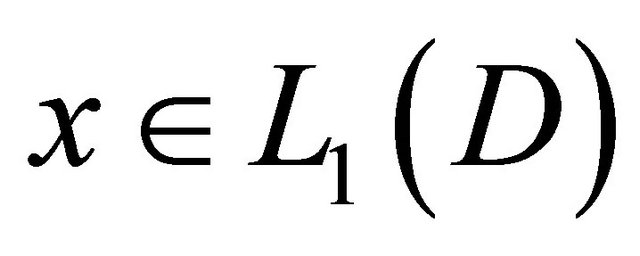where 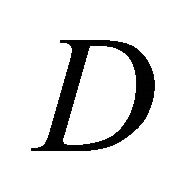is a nonempty and measurable subset of 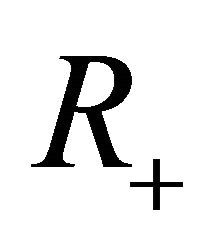then we extend 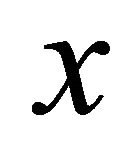to the whole half axis 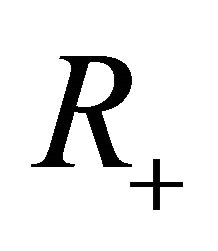by putting 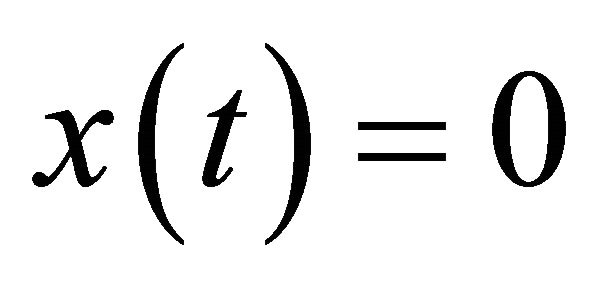for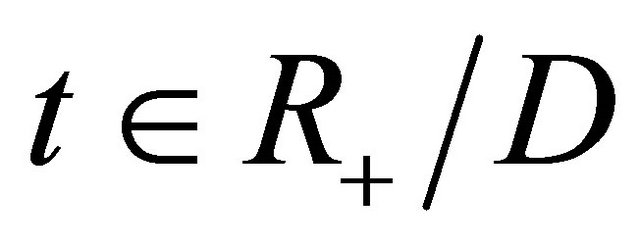. Then we can treat in the usual way. When the operator transforms 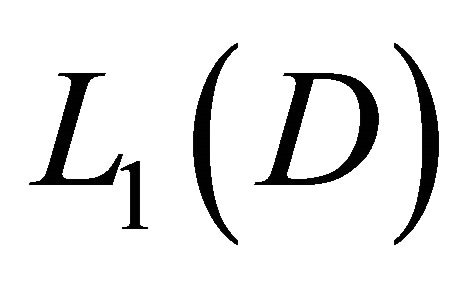into itself its norm will be denoted by.

2.3. Measures of Weak Noncompactness

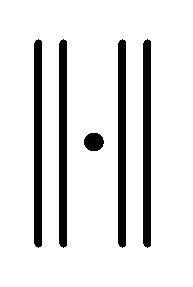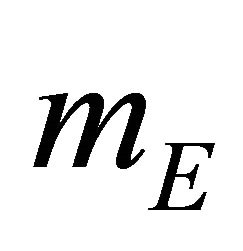Let us assume that is an infinite dimensional Banach space with the norm and the zero element. Denote by the family of all nonempty and bounded subsets of and by 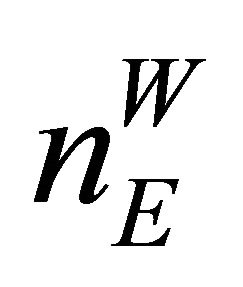its subfamily consisting of all relatively weakly compact sets. The symbol 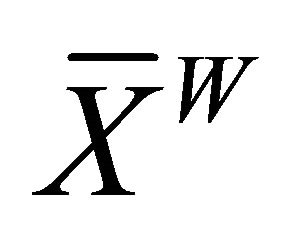stands for the weak closure of a set 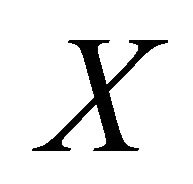and the symbol 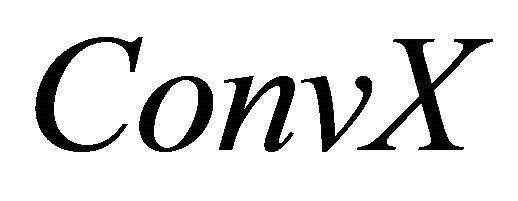will denote the convex closed hull (with respect to the norm topology) of a set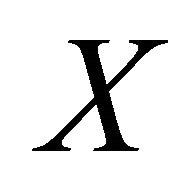. We denote by 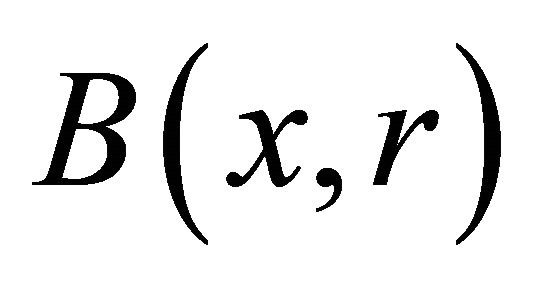the ball centered at 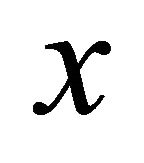and of radius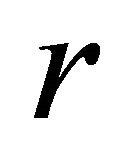. We write instead of 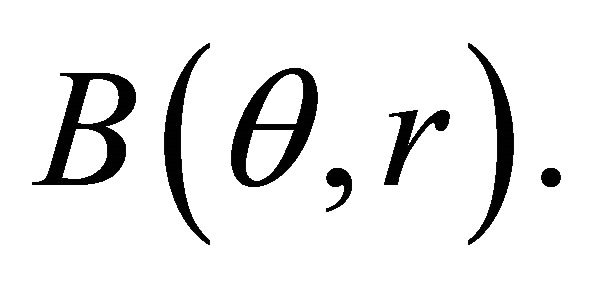In what follows we accept the following definition [16]

Definition 5. A function 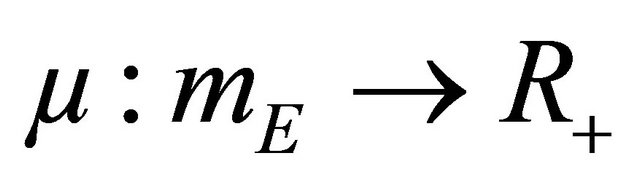is said to be a measure of weak noncompactness if it satisfies the following conditions: The Family 1) The family is nonempty and is nonempty and ker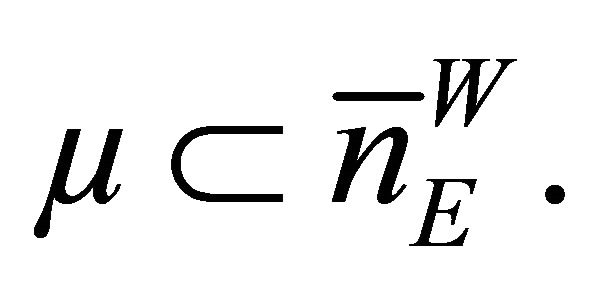

2)

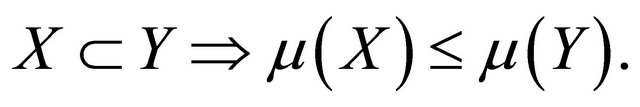
3)

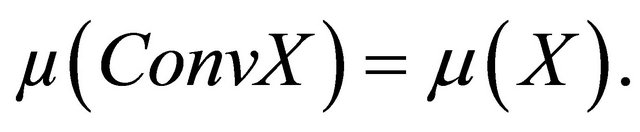
4) for .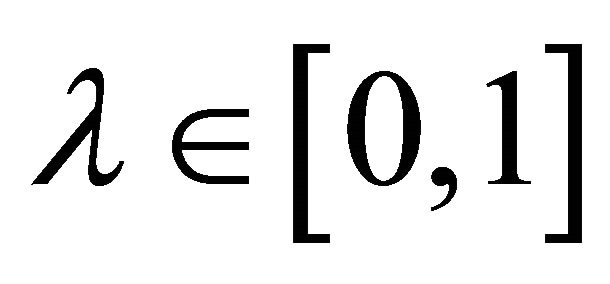

5)

And if then the intersection is nonempty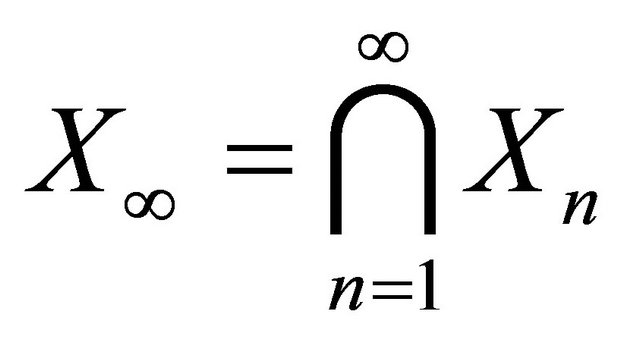

The family 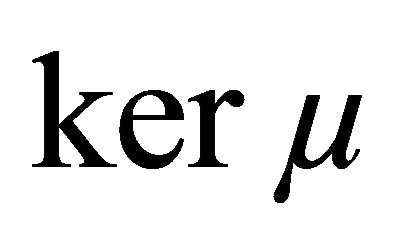is said to be the kernel of the measure of weak noncompactness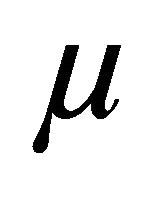. Let us observe that the intersection set 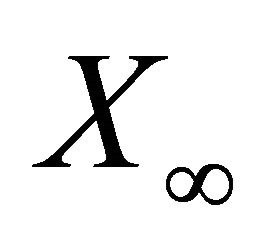from 5) belongs to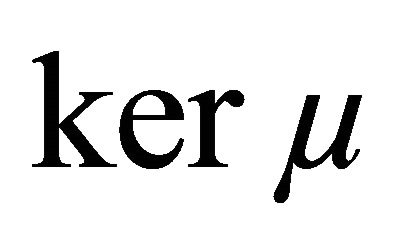. Indeed, since for every 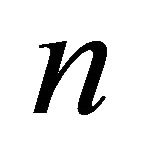then we have that

.

We can construct a useful measure of weak noncompactness in the space 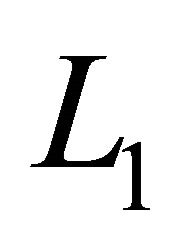that based on the following criterion for weak noncompactness due to Dieudonné [17,18].

Theorem 6. A bounded set 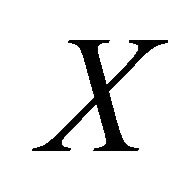is relatively weakly compact in 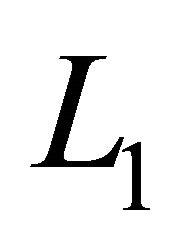if and only if the following two conditions are satisfied:

a) for any 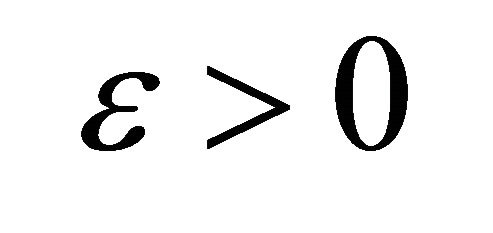there exists 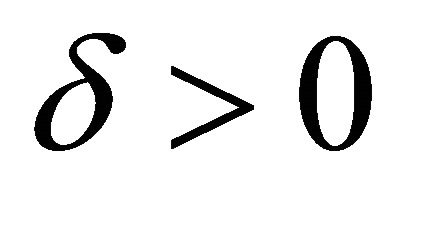such that if meas. 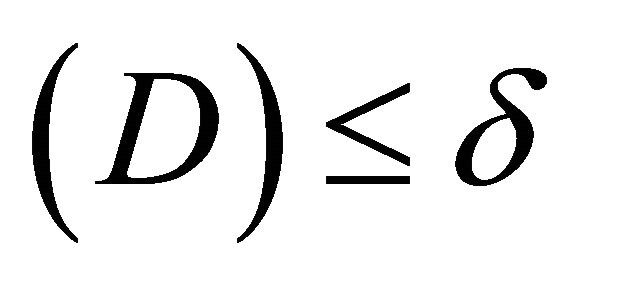Then 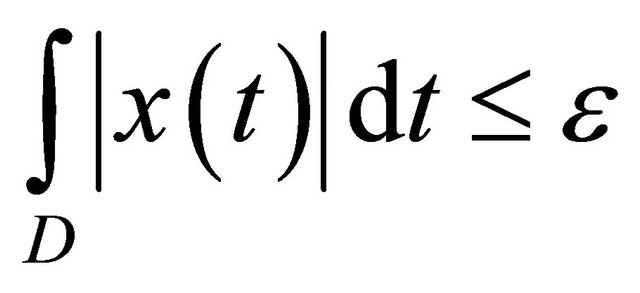for all,.

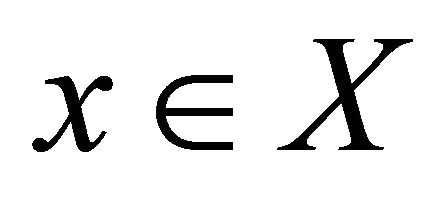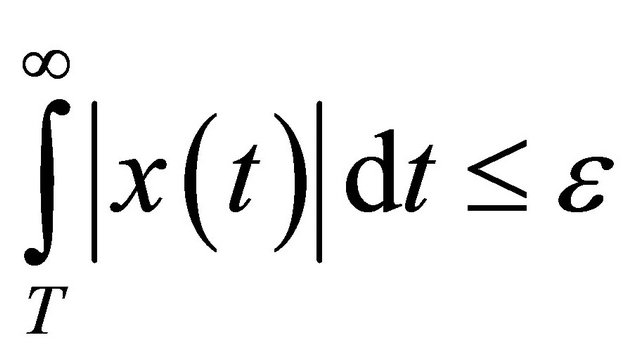b) for any there is such that for any ,.

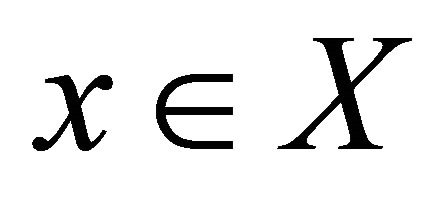Now, for a nonempty and bounded subset 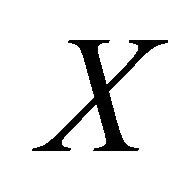of the space 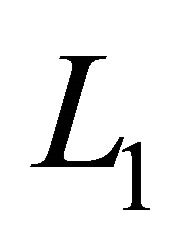let us define:

(3)

where

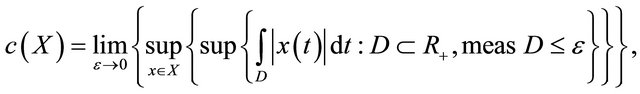
and

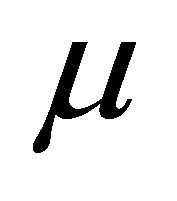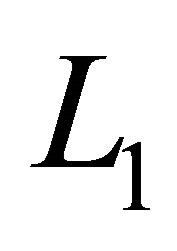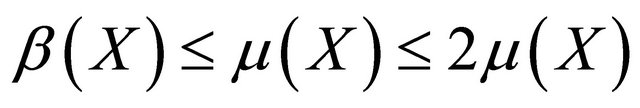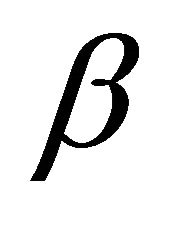It can be shown [17] that the function is a measure of weak noncompactness in the space such that, for any, where denotes the De Blasi measure of weak noncompactness in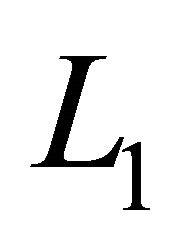. Moreover,.

In our approach we will need the following fixed point theorem due to Schauder.

Theorem 7. Let 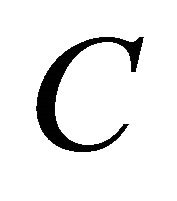be a nonempty, convex, closed, and bounded subset of a Banach space. Let be a completely continuous mapping. Then has at least one fixed point in.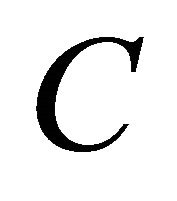

2.4. Fractional Calculus

The definitions of both differential operator and the integral operator of fractional order are stated as follows [19,20].

Definition 8. Let 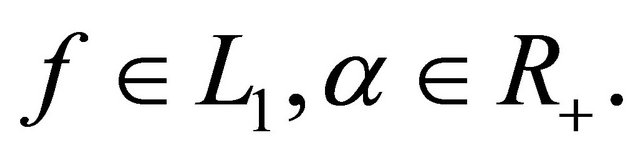The RiemmanLiouville (R-L) fractional integral of the function 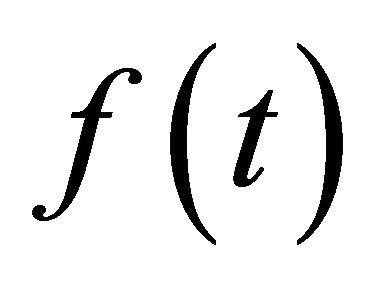of order is defined as

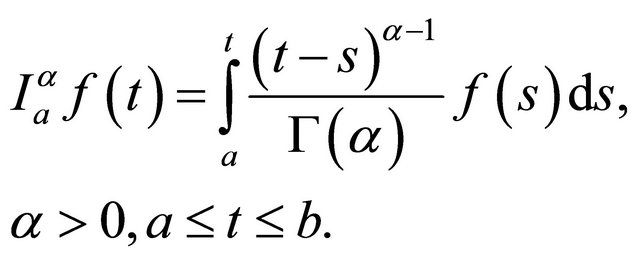
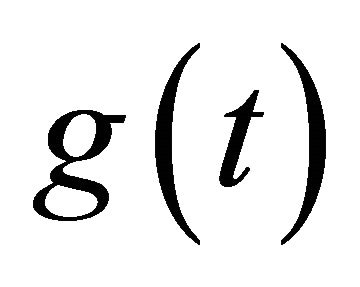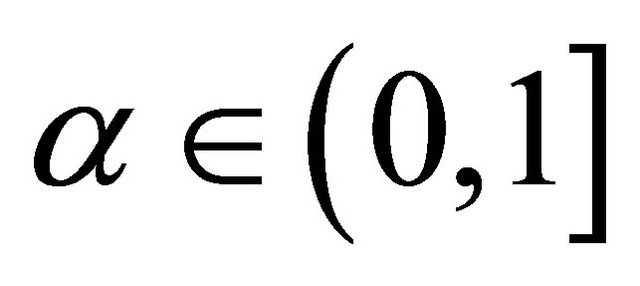Definition 9. Let be an absolutely continuous function on. Then the fractional derivative of order of 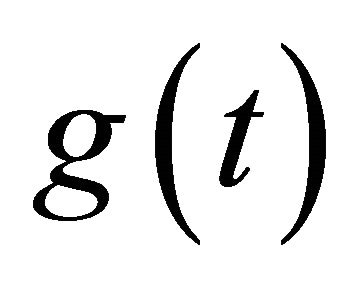is defined as

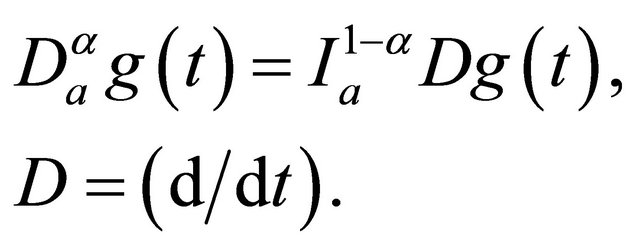
We state here some results concerning the above mentioned operators:

1) Let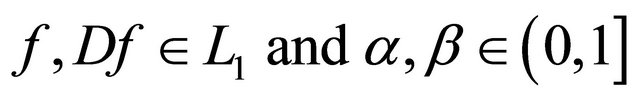, then i)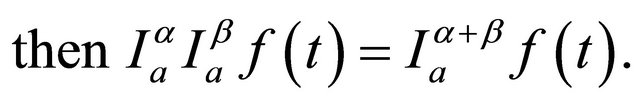

ii)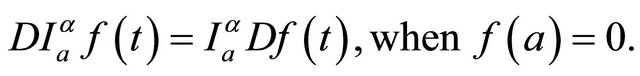

2) The operator 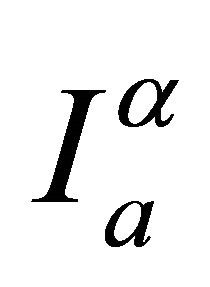maps 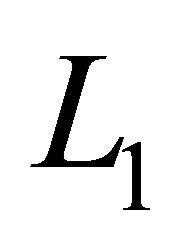into itself continuously.

3. Existence Theorem

Consider the integral Equation (2) and let denotes the operator determined by the right hand side of this equation, i.e.,

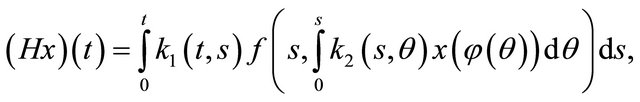(4)

where 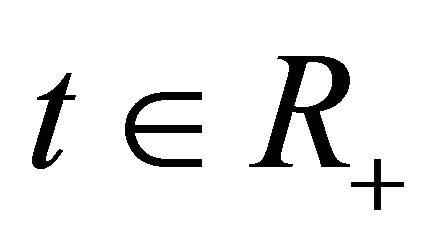In fact the operator can be written as the product 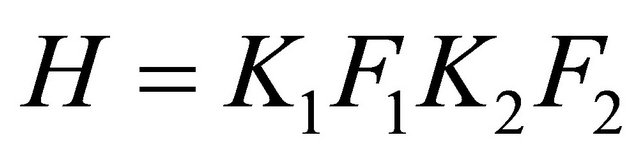of the linear Volterra operator

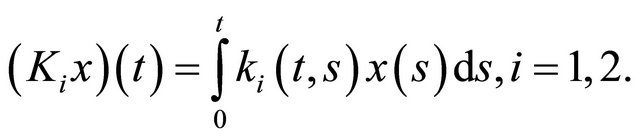
and the superposition operator

Therefore Equation (4) can be written as:

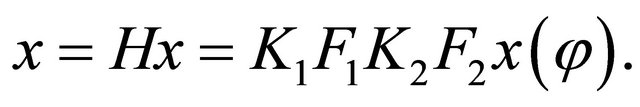(5)

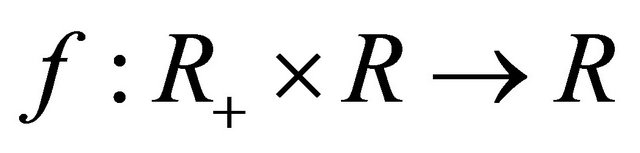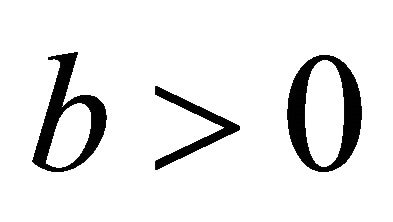To establish our main result concerning existence of an integrable solution of Equation (2) we impose suitable conditions on the functions involved in that equation. Namely we assume 1) The functions satisfy the Caratheodory conditions and there exist functions and constants such that

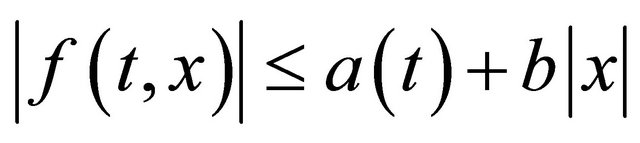
holds for all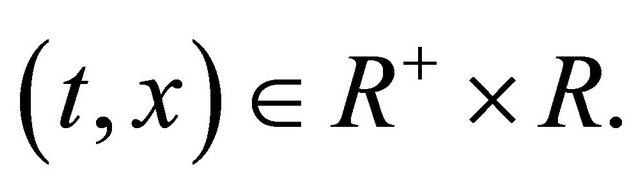

2) The functions 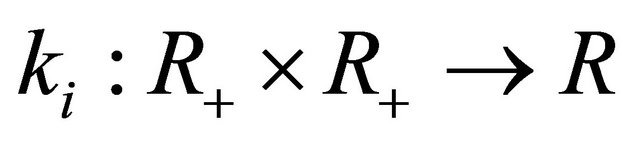satisfy the Caratheodory conditions and the linear Volterra operators 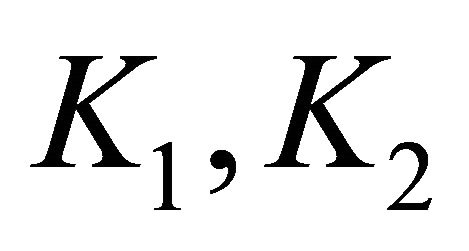associated with 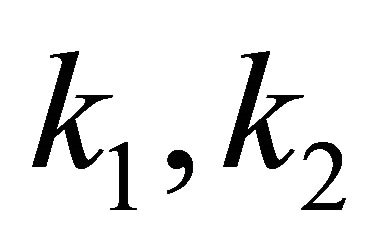map 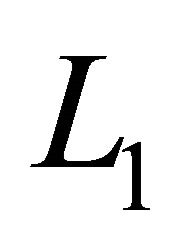into itself.

3) 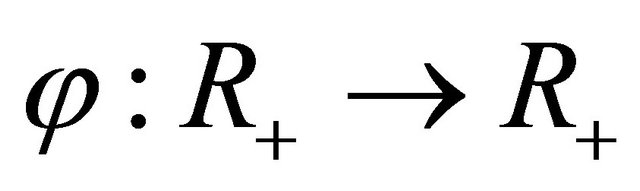is increasing, absolutely continuous and there exists a constant 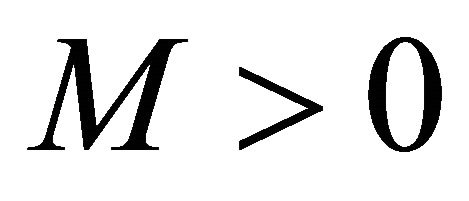such that 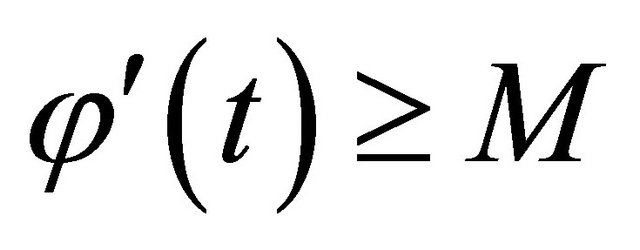a.e. on.

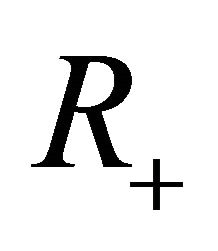4).

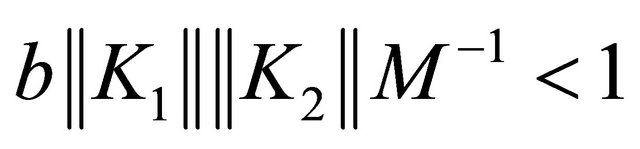Now we can state our main result in the next theorem.

Theorem 10. Under the above assumptions the Equation (2) has at least one solution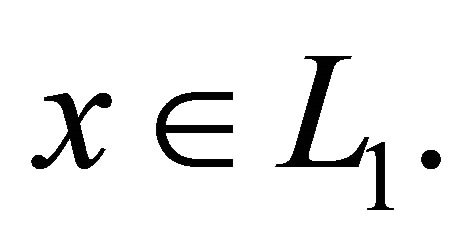

Proof. Since is a nonlinear operator defined by Equation (5), then based on assumptions i) and ii) if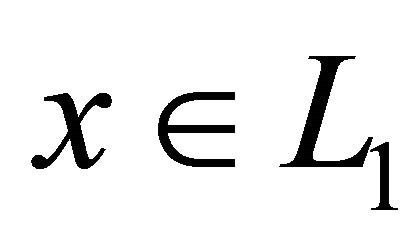, then 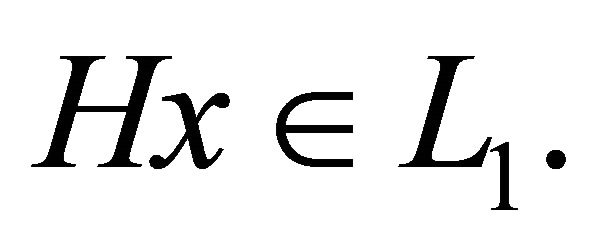Moreover, from Equation (5), and noting that 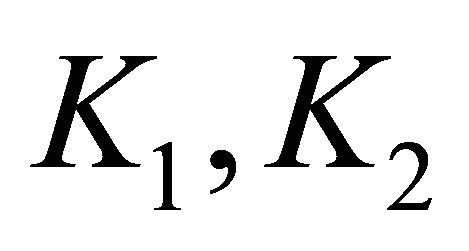according to our assumptions are indeed bounded, we have

The above estimate shows that the operator maps 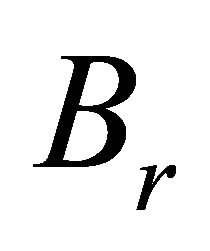into itself, where

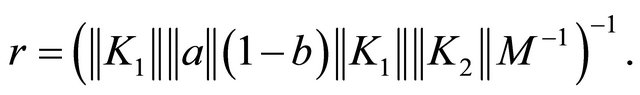
Moreover, according to Theorem 2, we deduce that the operator is continuous on the space.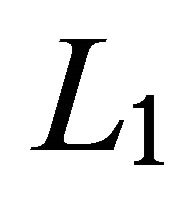

Next, to prove that is a contraction, let be a nonempty subset of 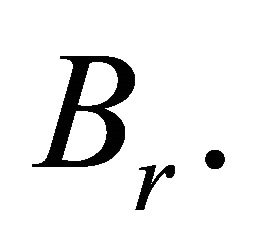Fix 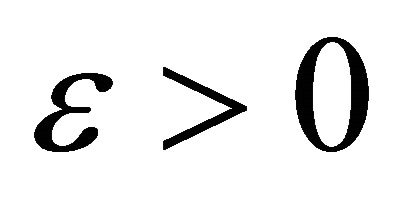and take a measurable subset 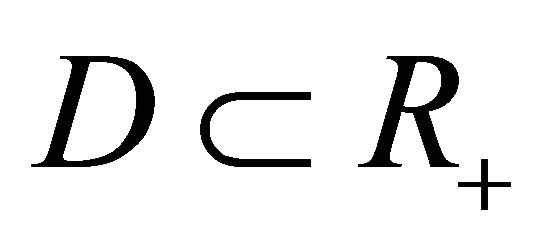such that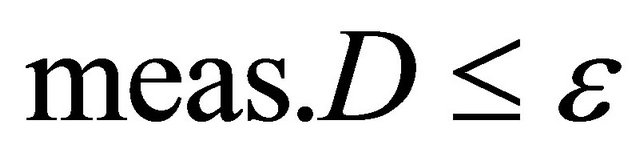. Then for any, we get

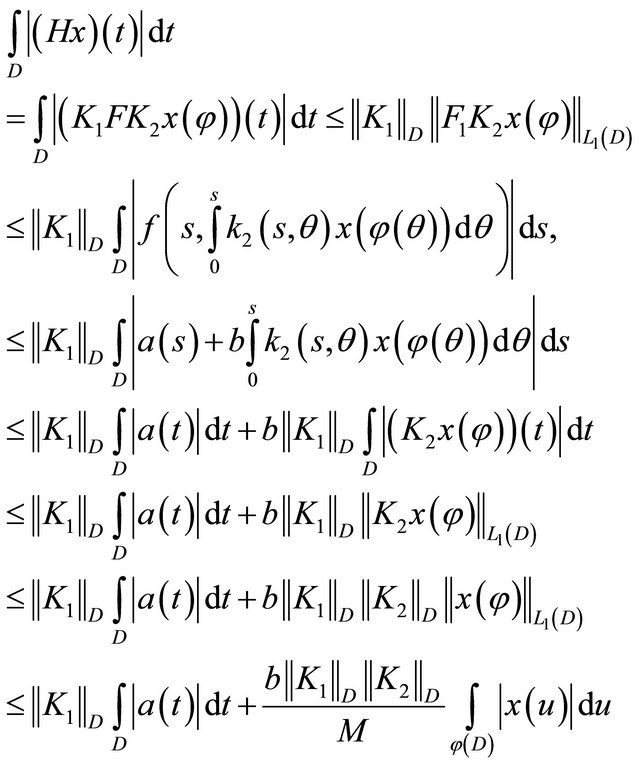
where the symbol 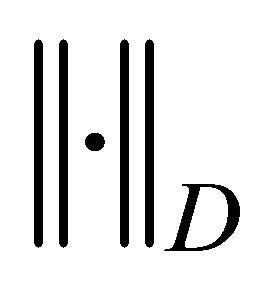denotes the operator norm acting from the space 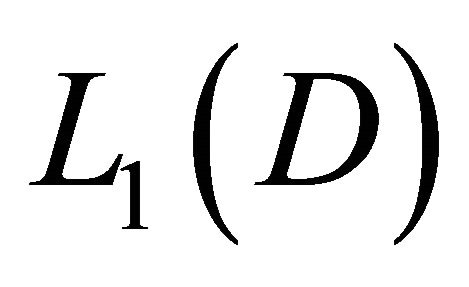into itself. Also in the above calculation we used the fact that 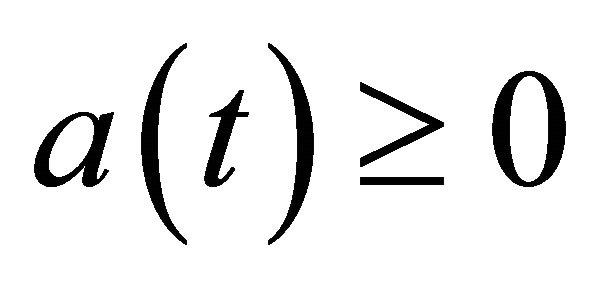for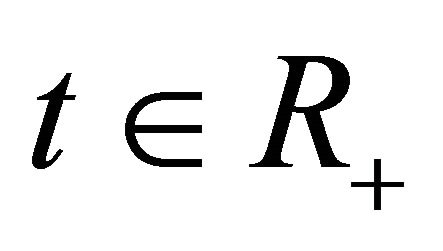. From the absolute continuity of the function and the obvious equality

.

and using Theorem 6 we obtain

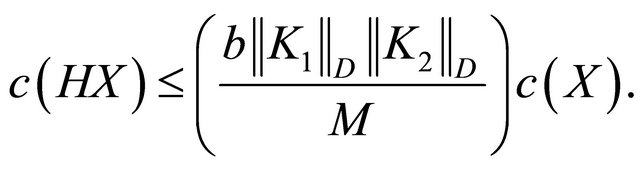(6)

Furthermore, fixing we can deduce that

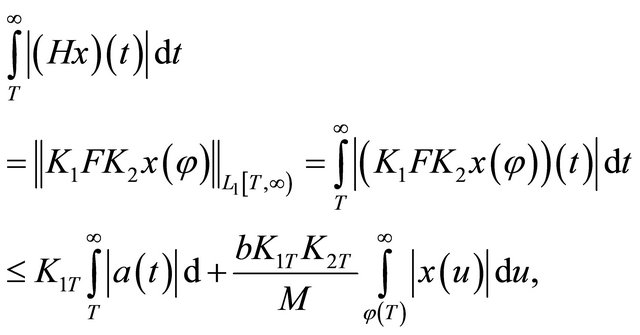
where the symbol 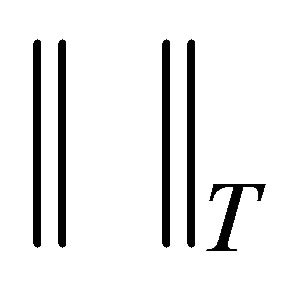denotes the operator norm acting from the space 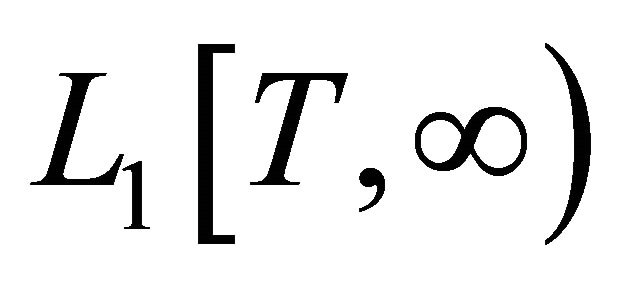into itself. Now according to the fact that the set consisting of one element is weakly compact, by using Theorem 6 and the formula

and since we get

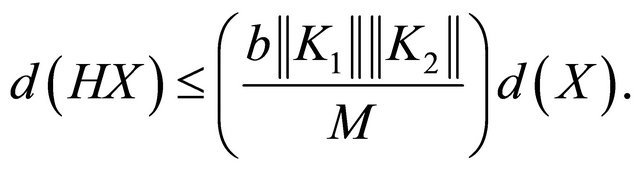(7)

According to Equation (3), combining (6) and (7), we get

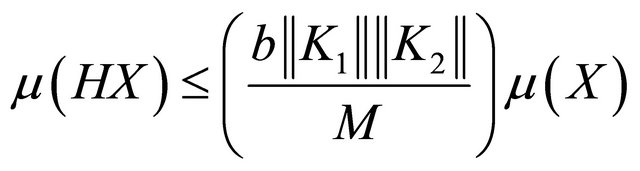(8)

Put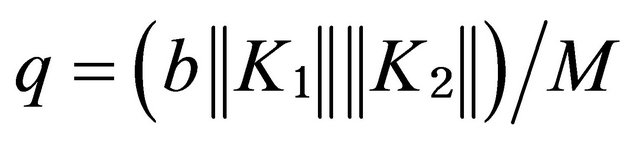. Clearly, according to assumption iv). Consider the sequence of sets

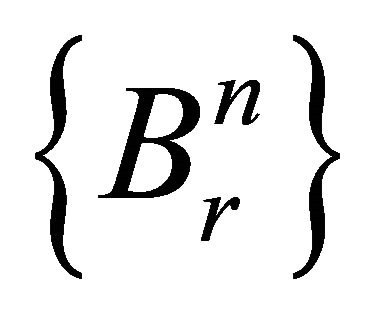, where 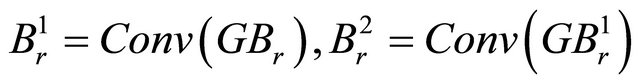and so on. Obviously this sequence is decreasing i.e. 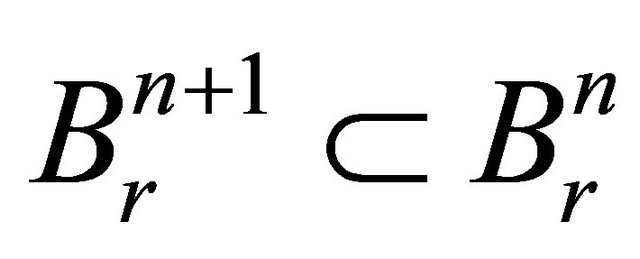for 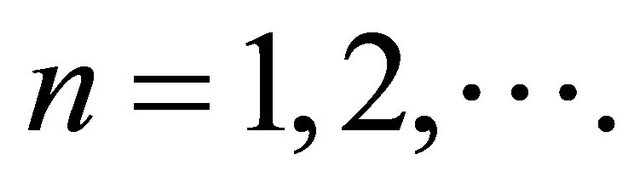Moreover,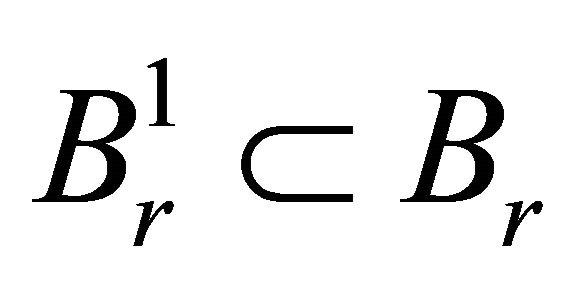. Apart from this, all sets belonging to this sequence are closed and convex, so weakly closed. On the other hand in view of inequality (8) we have

which yields that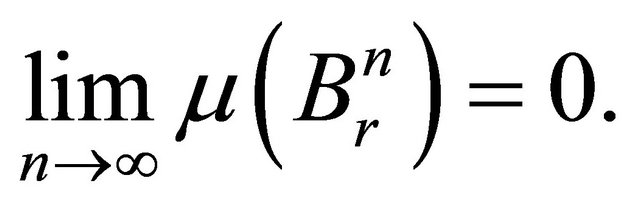

Consequently, by axiom 5) of Definition 5 we infer that the set

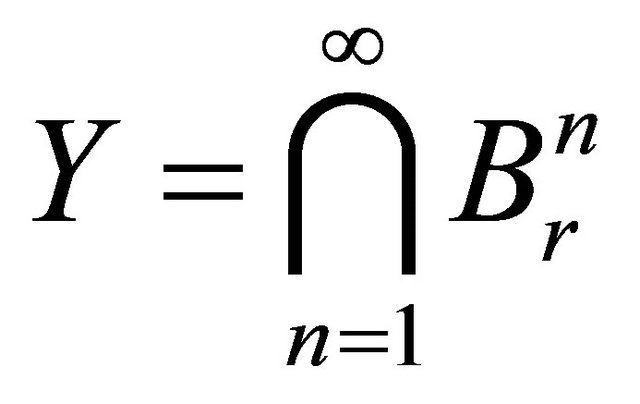
is nonempty, closed, convex and weakly compact (in view of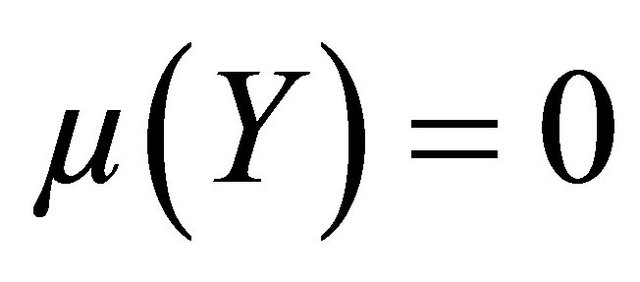). Moreover,.

In the sequel we show that the set 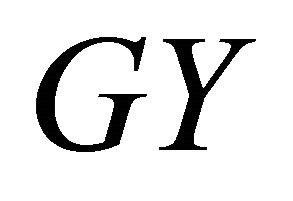is relatively compact in the set.

To do this let us take an arbitrary sequence 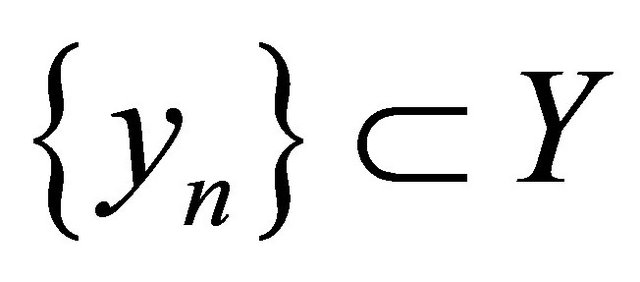and fix arbitrarily a number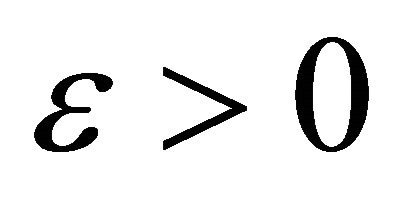. Since is weakly compact, in view of Theorem 6 we deduce that there exists 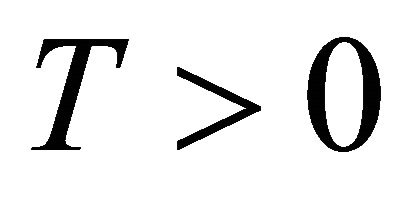such that for any natural number the following inequality is satisfied

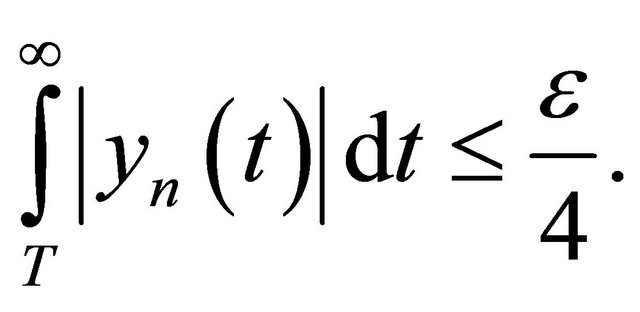(9)

To apply the classical Schauder fixed point theorem, we need to prove that the set 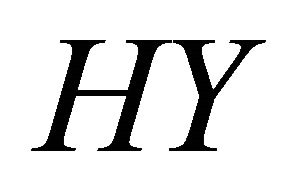is relatively compact in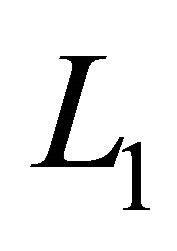. For this aim let us consider the functions on the set and the functions on the set

.

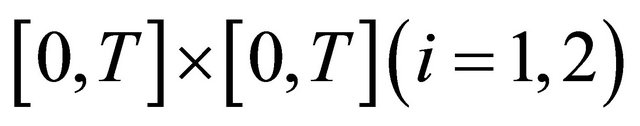In view of Theorem 3 we can find a closed subset of the interval 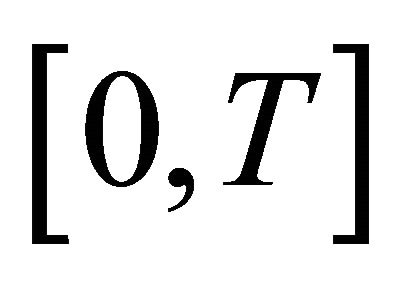such that 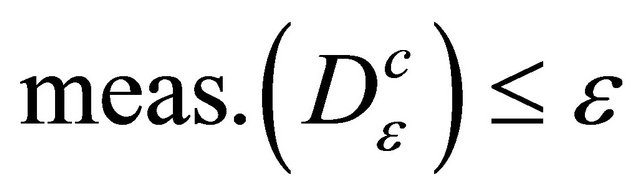(where

) and such that the functions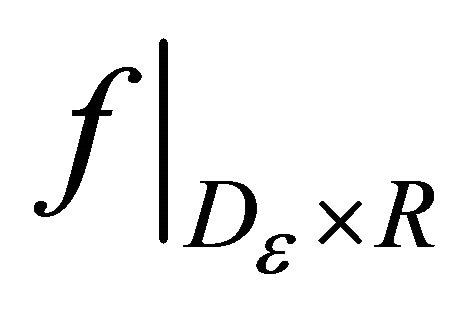

and are continuous. Hence we infer that are uniformly continuous.

In what follows we show that 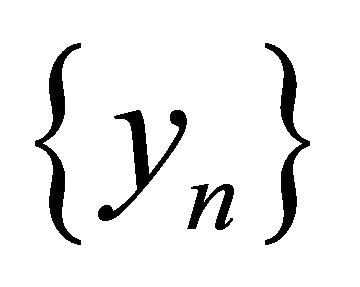is an equicontinuous on, for that let us take arbitrarily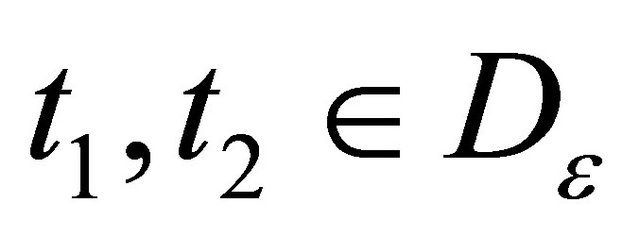. Without loss of generality we can assume that. Then, keeping in mind our assumptions, for an arbitrary fixed 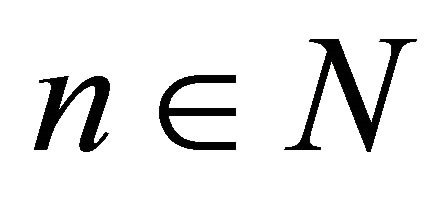we obtain:

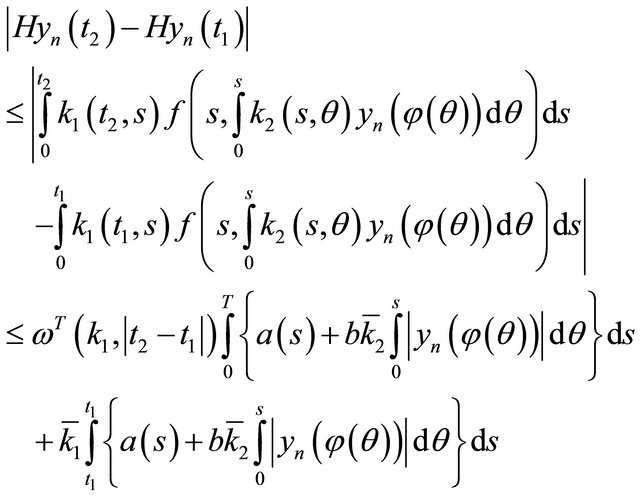
where 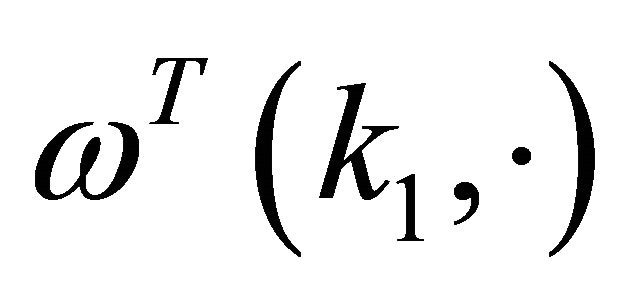denotes the modulus of continuity of the function 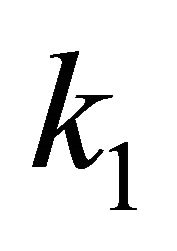on the set 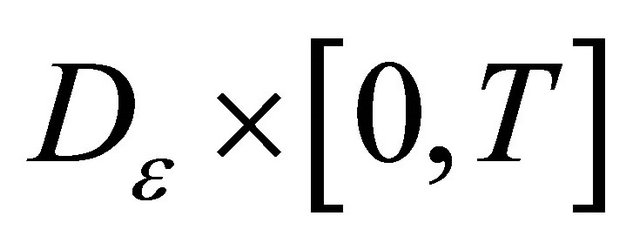and

By rearranging the order of double integrations, we get

From the above estimate and the consideration of the fact that 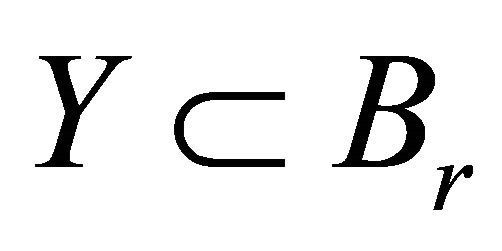we obtain

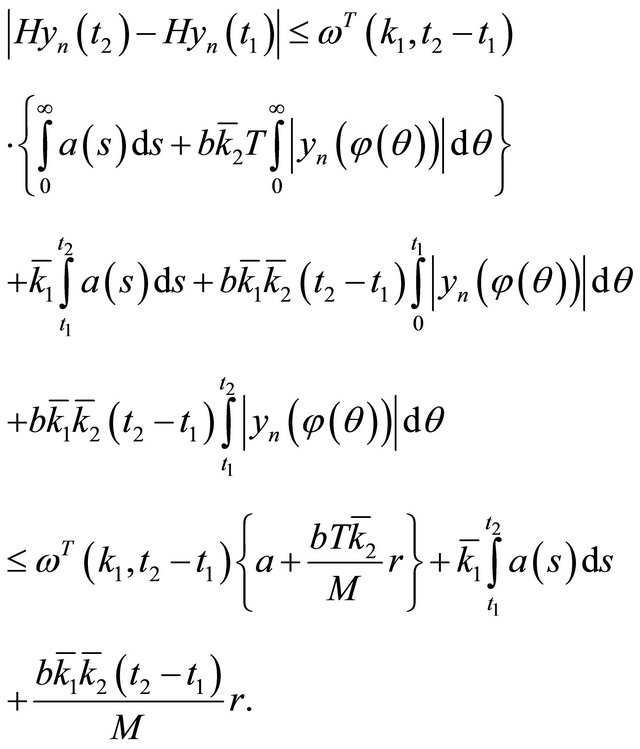
Now, utilizing the fact that the sequence 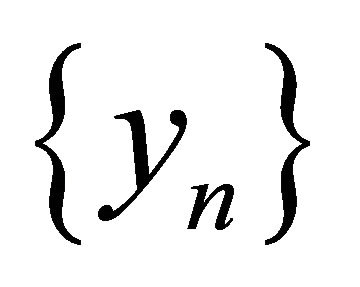is weakly compact and taking into account Theorem 6 we can show that the number

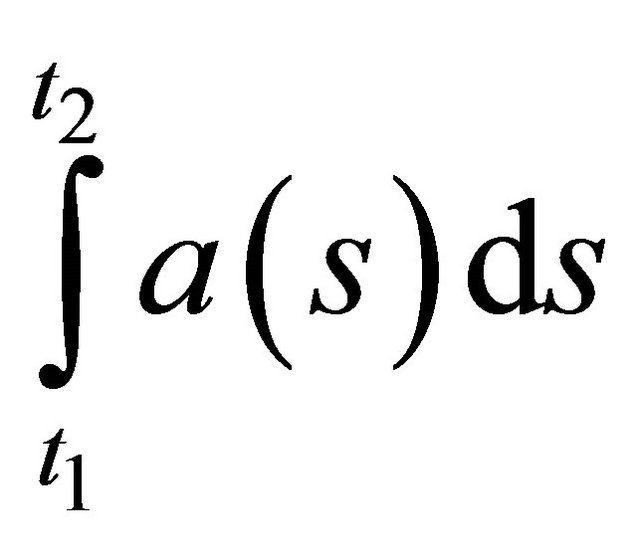
is arbitrarily small provided the number is taken to be sufficiently small (it is a consequence of the fact that a one element set is weakly compact in).

Furthermore,

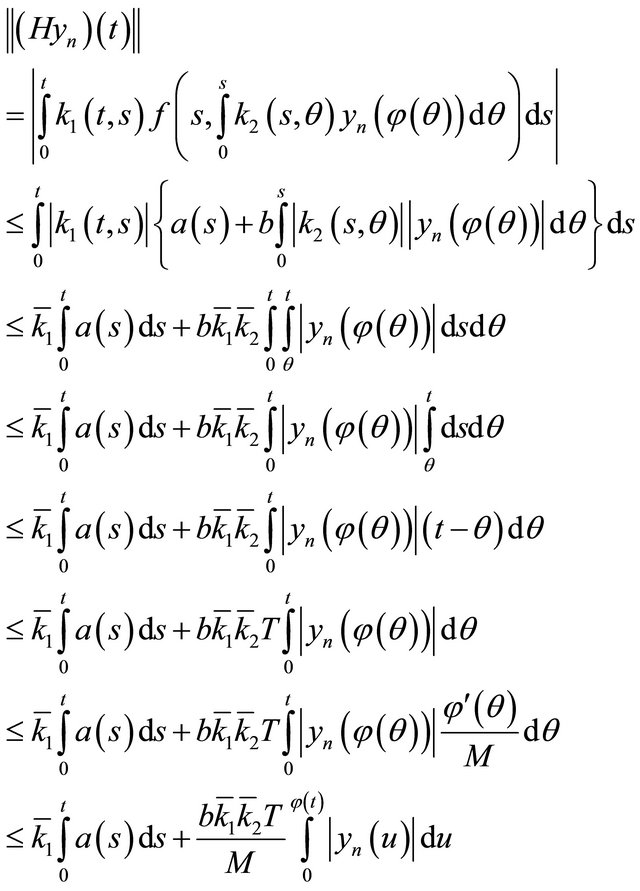
Hence

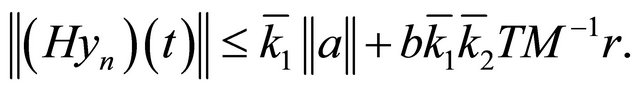
Hence consequently the sequence is a sequence of uniformly bounded and equicontinuous functions on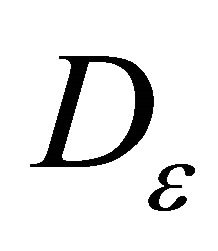. Hence, in view of Ascoli-Arzela theorem we deduce that the sequence 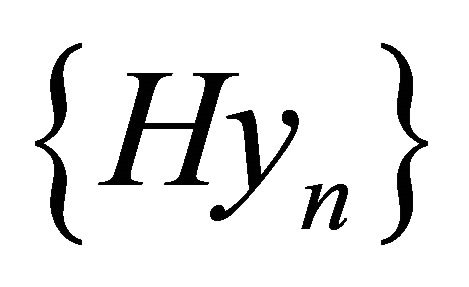is relatively compact subset in the space.

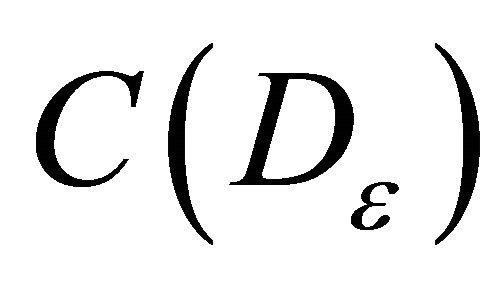Further observe that the above reasoning does not depend on the choice of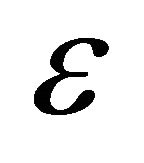. Thus we can construct a sequence 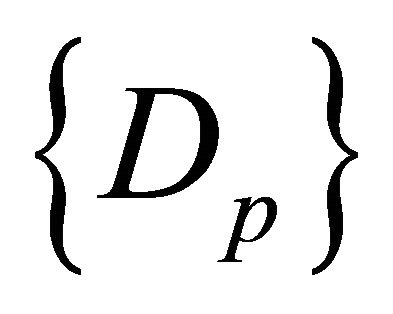of closed subsets of the interval 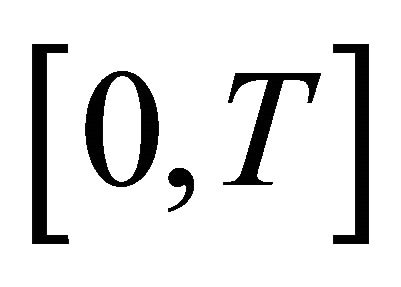such that 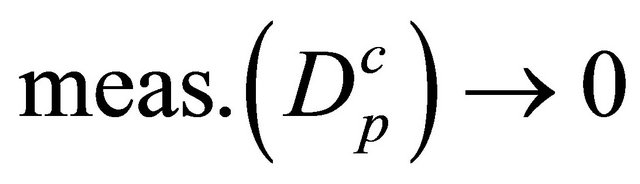as and such that the sequence 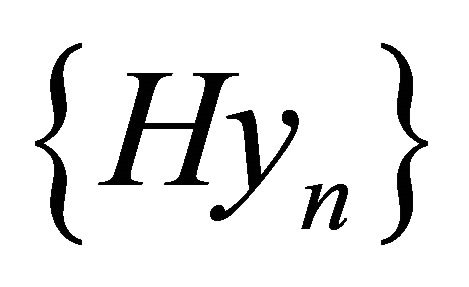is relatively compact in every space

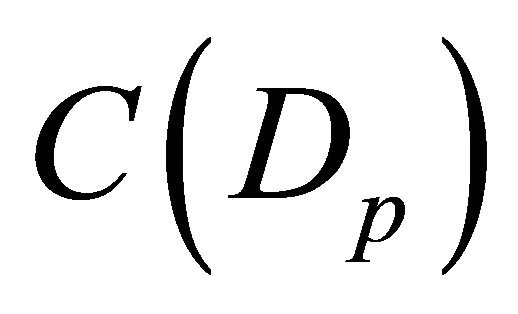. Passing to subsequences if necessary we can assume that 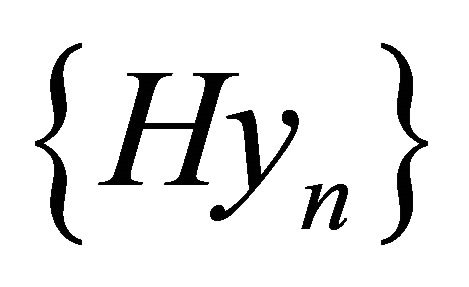is a Cauchy sequence in each space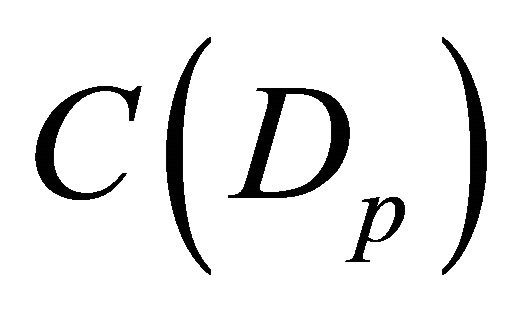, for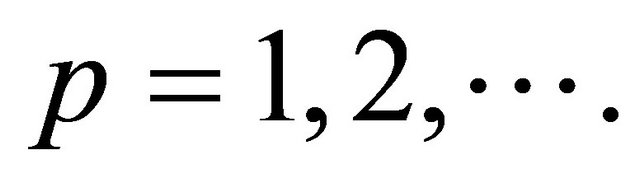

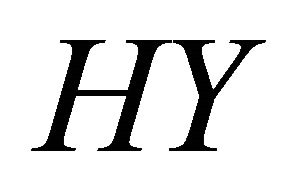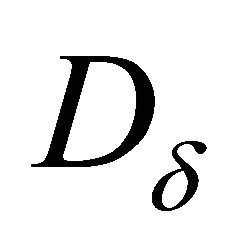In what follows, utilizing the fact that the set is weakly compact, let us choose a number such that for each closed subset of the interval such that we have

(10)

for any.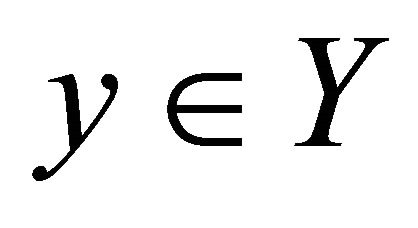

Keeping in mind the fact that the sequence 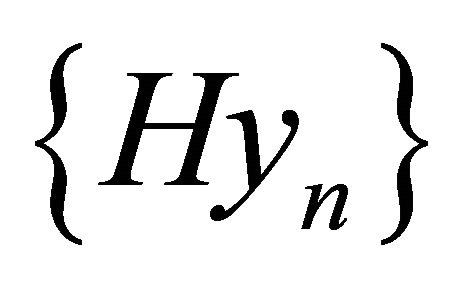is a Cauchy sequence in each space 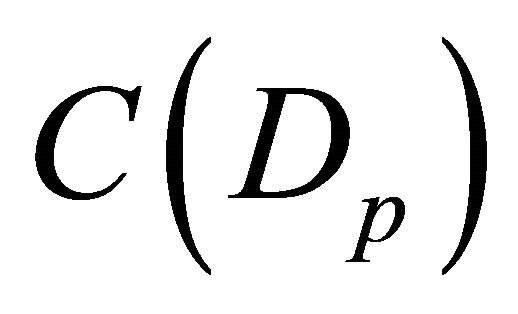we can choose a natural number 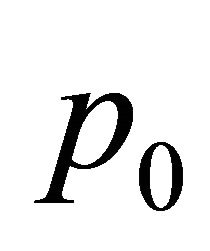such that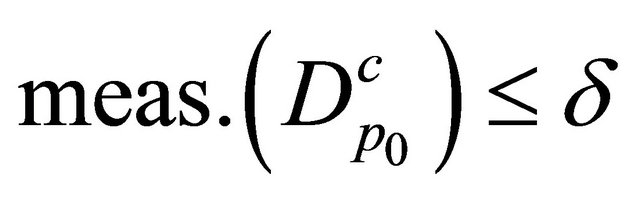

and for arbitrary natural numbers the following inequality holds

for any. Obviously without loss of generality we can assume that.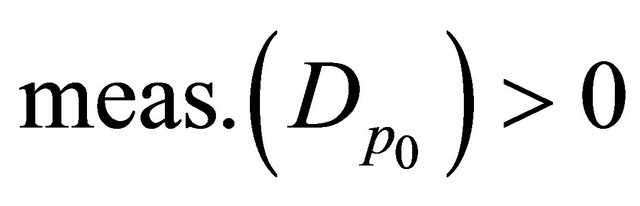

Now, using the above facts and (10) we obtain

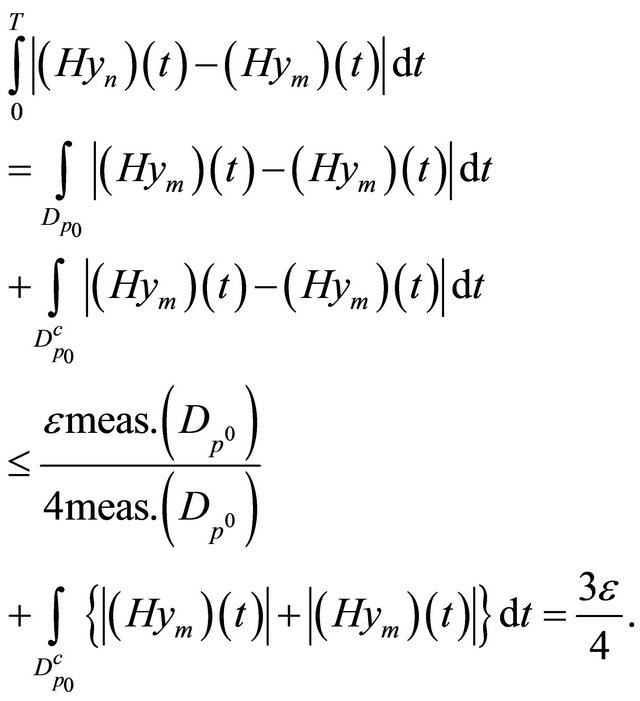(11)

Finally, from (10) and (11) we get

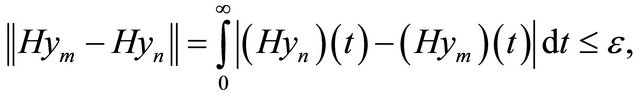
which means that 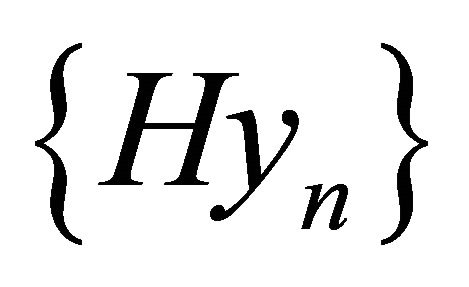is a Cauchy sequence in the space Hence we conclude that the set 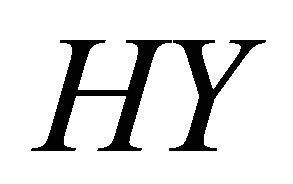is relativelycompact in this space.

In the last step of the proof let us consider the set 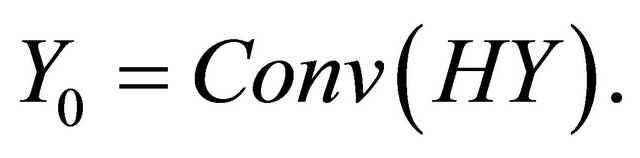In view of the Mazur theorem we infer that the set 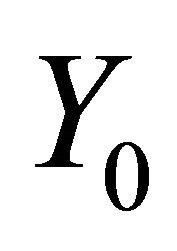is compact in the space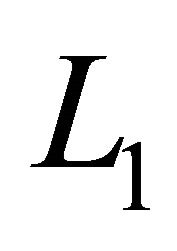. Moreover, we have that the operator transforms continuously the set 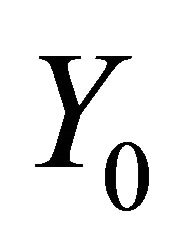into itself. Thus the classical Schauder fixed point principle gives that has at least one fixed point. This proves that there exists at least one 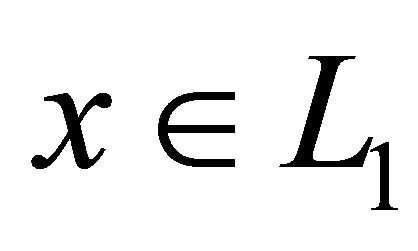that solves Equation (4).

4. Nonlinear Equation of Convolution Type

Assume that 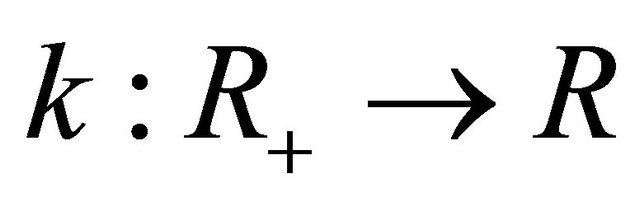is an integrable function. For an arbitrary function 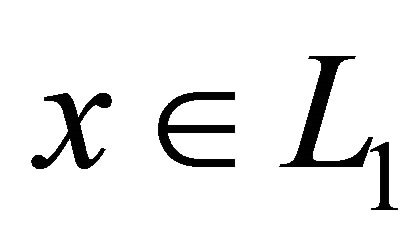set

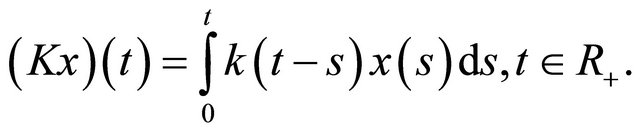
This operator is a linear integral operator of convolution type and maps 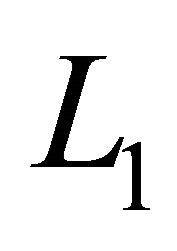into itself continuously.

Now, consider the following condition

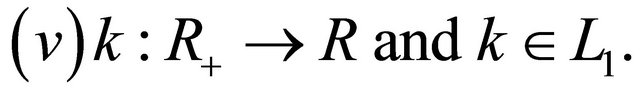
Then we have the following Corollary

Corollary 11. Let the hypotheses i)-v) are satisfied. Then a nonlinear equation of convolution type

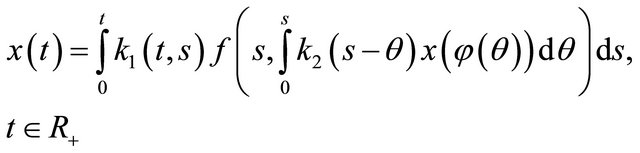(12)

has at least one integrable solution.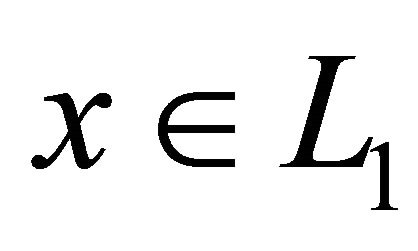

In the next subsection, we prove an existence theorem for integral equation of fractional order as a special form of Equation (12).

Initial Value Problems of Fractional Order

As a special case of Equation (14), we consider

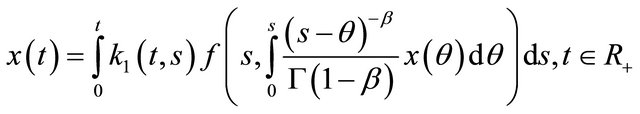(13)

where

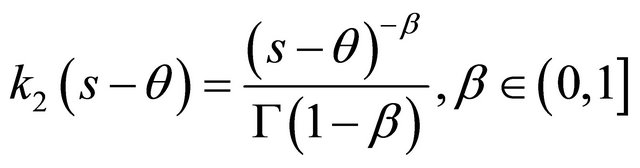
and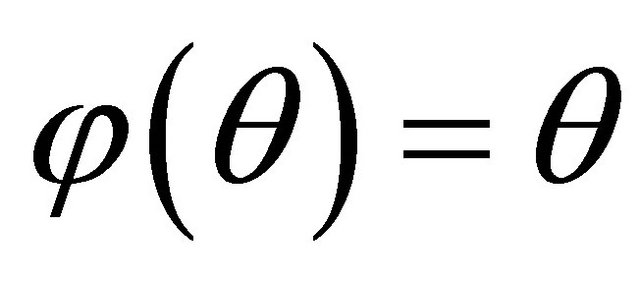. Equation (13) is an integral equation of fractional order that can be written in the form

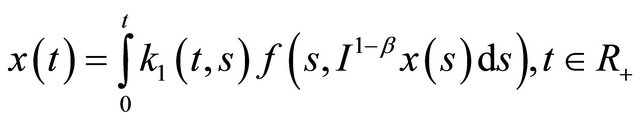(14)

Obviously, Equation (14) has at least one integrable solution.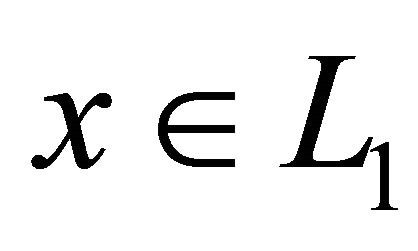

Definition 12. By a solution of the initial value problem (1) we mean an absolutely continuous function x satisfies the initial value problem (1).

Theorem 13. Let 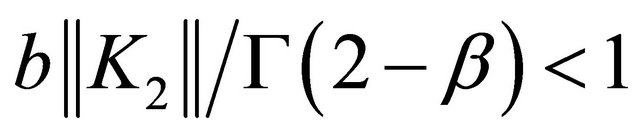and.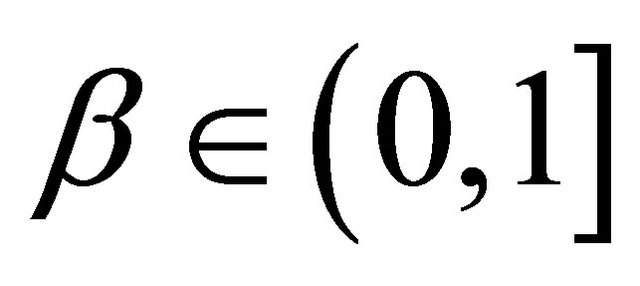

If assumptions i)-iii) and v) are satisfied, then the initial value problem (1) has at least one solution.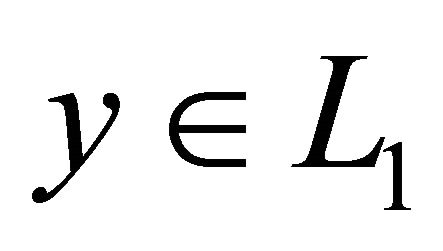

Proof. Let 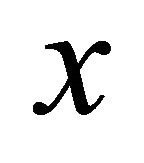be a solution of the integral Equation (14). Putting

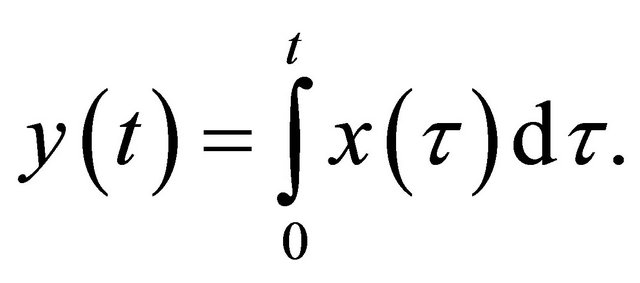
Since 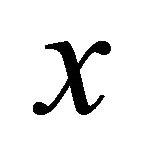is integrable, then

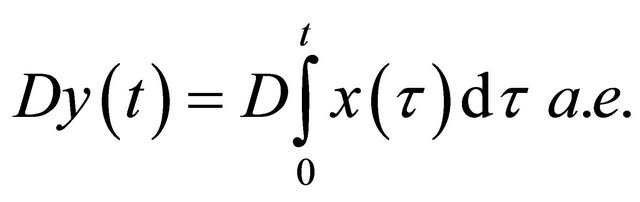
where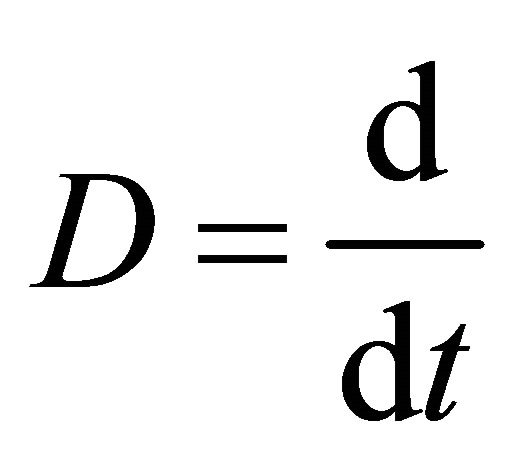. Moreover, the integral 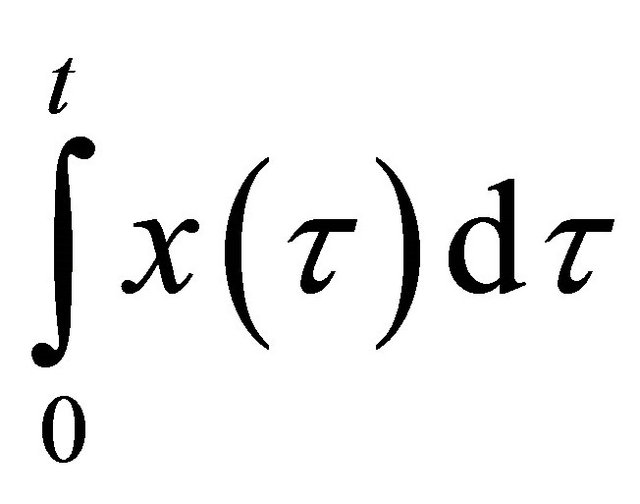of integrable function 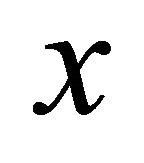is absolutely continuous then

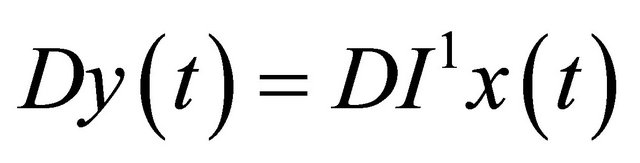
Then we have,

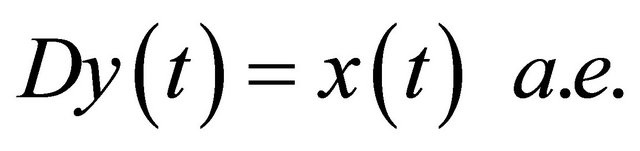
Furthermore, we obtain

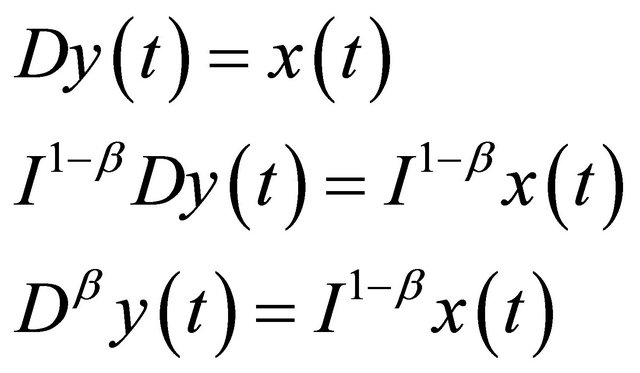
Consequently, Equation (14) gives

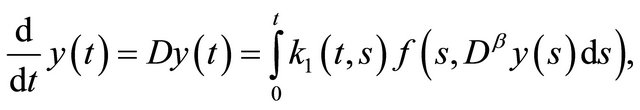
Since 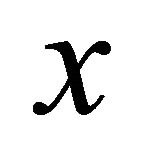is integrable and absolutely continuous, then

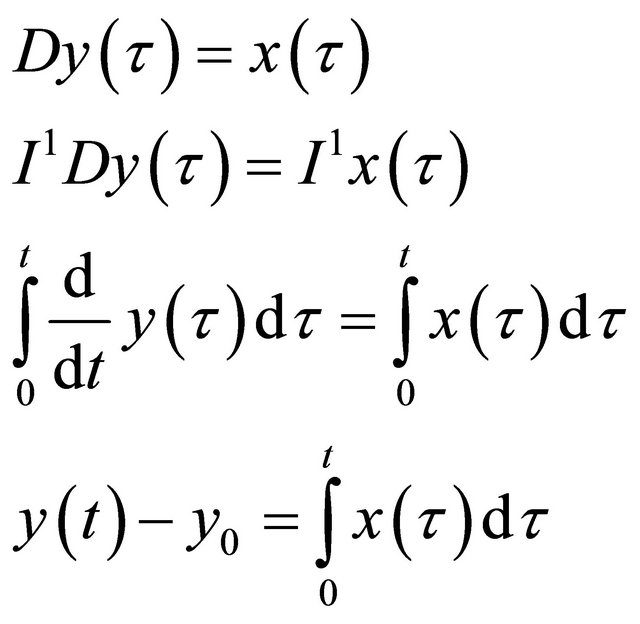
Clearly,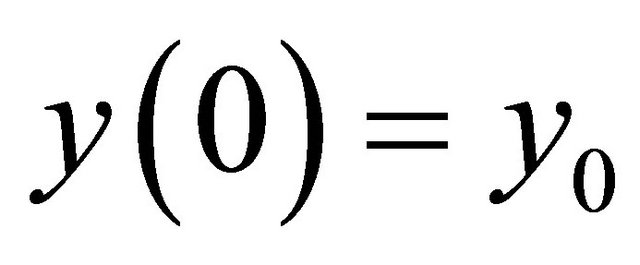. Hence we deduce that is an absolutely continuous function satisfies the initial value problem (1). Hence the proof is complete.

5. Conclusion

The existence theorem of functional integrable equation in the space of Lebesgue integrable functions on unbounded interval is presented and proved. As an application of this theorem, we investigated the existence of solution of the suggested initial value problems of fractional order.

REFERENCES