Applied Mathematics
Vol.4 No.1(2013), Article ID:27210,6 pages DOI:10.4236/am.2013.41020
Solving a Nonlinear Multi-Order Fractional Differential Equation Using Legendre Pseudo-Spectral Method
College of Civil Engineering and Mechanics, Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Xiangtan, China
Email: yangyinxtu@xtu.edu.cn
Received October 10, 2012; revised November 14, 2012; accepted November 21, 2012
Keywords: Legendre Pseudo-Spectral Method; Multi-Order Fractional Differential Equations; Caputo Derivative
ABSTRACT
In this paper, we apply the Legendre spectral-collocation method to obtain approximate solutions of nonlinear multiorder fractional differential equations (M-FDEs). The fractional derivative is described in the Caputo sense. The study is conducted through illustrative example to demonstrate the validity and applicability of the presented method. The results reveal that the proposed method is very effective and simple. Moreover, only a small number of shifted Legendre polynomials are needed to obtain a satisfactory result.
1. Introduction
Many phenomena in engineering physics, chemistry, and other sciences can be described very successfully by models that use mathematical tools of fractional calculus, i.e. the theory of derivatives and integrals of non-integer order [1-3]. For example, they have been successfully used in modeling frequency dependent damping behavior of many viscoelastic materials. There are numerous research which demonstrate the applications of fractional derivatives in the areas of electrochemical processes, dielectric polarization, colored noise, and chaos.
The numerical solution of differential equations of integer order has been a hot topic in numerical and computational mathematics for a long time. The solution of fractional differential equations has been recently studied by numerous authors. However, the state of the art is far less advanced for general fractional order differential equations. Moreover, to the best of the authors knowledge, very few algorithms for the numerical solution of Multi-order Fractional Differential Equations (M-FDEs) have been suggested [4-6], particularly algorithms for analytical solutions and approximate solutions of nonlinear M-FDEs.
As we know, the fractional derivatives are global dependence problems (they are definite by the integral in [0, t]), from this point, the global methods—spectral methods maybe are more suit to solve the FDEs. As we know the standard spectral methods possess infinite order of accuracy for the equations with well regularity solutions, while fail to many complicated problems with singular solutions. So, it is attracted considerable interest that how to enlarge the adaptability of spectral methods, and construct certain simple approximation schemes without loss of any accuracy to even more complicated problems. It is well known that Legendre polynomials are well known family of orthogonal polynomials on the interval [−1, 1]. They are widely used because of their good properties in the approximation of functions [7-9]. For multi-order fractional differential equation, a operational matrix is studied [4], Chebyshev wavelets is considered in [10], adomian decomposition is considered in [11], a variational iteration method is considered in [12], predictor-corrector method is studied in [13], operator splitting method is considered in [14], and Adams method is researched in [15]. In this paper, we introduce the Legendre pseudo-spectral method to solve multi-order arbitrary differential equations, which include the linear and nonlinear differential equations.
The outline of this paper is as follows. In Section 2, we review the basic definitions and the properties of the fractional calculus. In Section 3, the approximation of fractional derivative by Legendre Polynomials is obtained. In Section 4, we present the application of the Legendre pseudo-spectral method to multi-order fractional differential equation. Some numerical examples are provided in Section 5. Also a conclusion is given in Section 6.
2. Fractional Calculus
In this section, we first review the basic definitions and the operational properties of fractional integral and derivative for the purpose of acquainting with sufficient fractional calculus theory. Many definitions and studies of fractional calculus have been proposed in the past two centuries. These definitions include Riemann-Liouville, Reize, Caputo and Grnwald-Letnikov fractional operators. The two most commonly used definitions are the Riemann-Liouville operator and the Caputo operator. We give some definitions and properties of the fractional calculus.
 denotes Caputo fractional derivative of order
denotes Caputo fractional derivative of order ![]() is defined
is defined
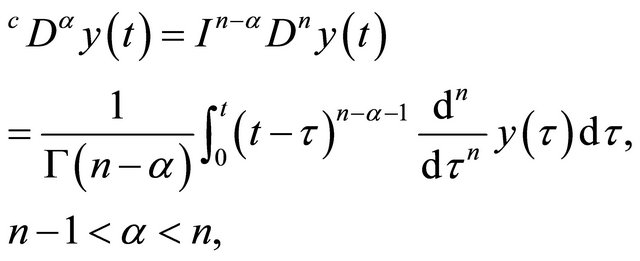 (1)
(1)
where 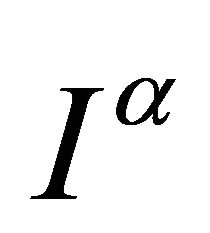 denotes the Riemann-Liouville fractional integral of order order
denotes the Riemann-Liouville fractional integral of order order ![]() defined as
defined as
 (2)
(2)
As we all know, there are some different definitions of fractional operator except the Caputo fractional derivative. From a theoretical point of view the most natural approach is the Riemann-Liouville definition defined as
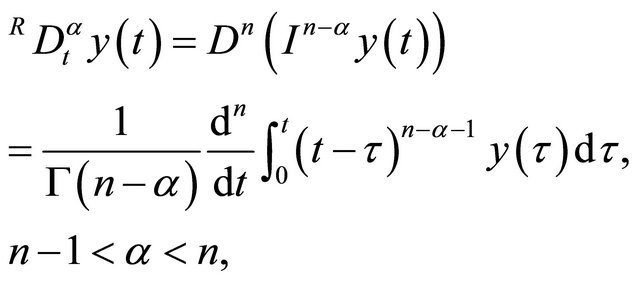
The relationship between the Caputo definition and the Riemann-Liouville definition can be given by the following formula
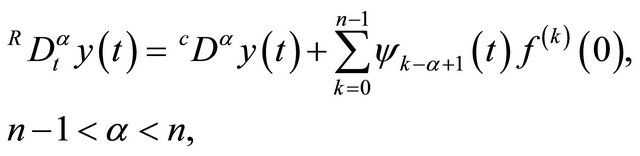
where

Similar to integer-order differentiation, Caputo’s fractional differentiation is a linear operation:
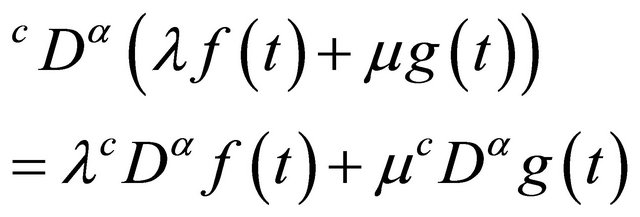
For the Caputo and Riemann-Liouville’s derivative we have:
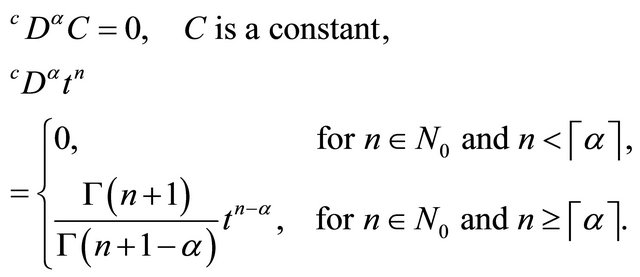 (3)
(3)
Amongst a variety of definition for fractional order derivatives, Caputo fractional derivative has been used because it allows physically interpretable initial conditions.
3. Evaluation of the Fractional Derivative Using Legendre Polynomials
The well known Legendre polynomials are defined on the interval 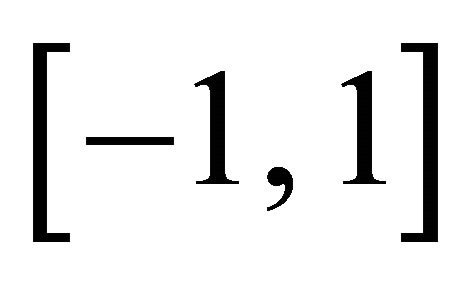 and can be determined with the aid of the following recurrence formula:
and can be determined with the aid of the following recurrence formula:
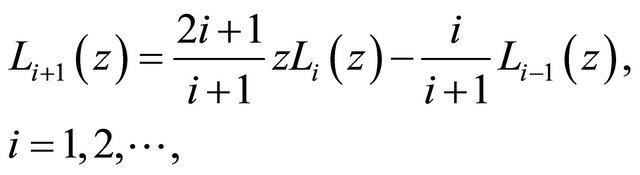 (4)
(4)
where 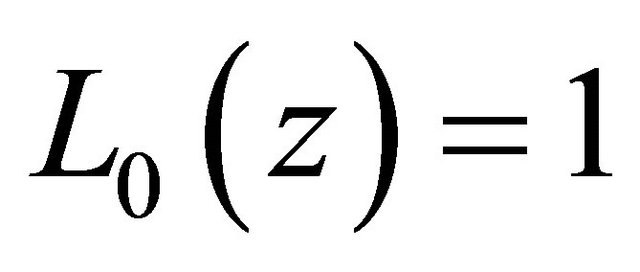 and
and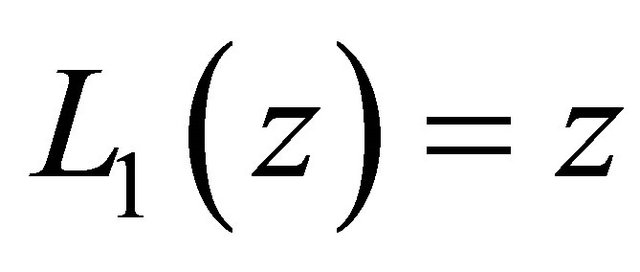 . In order to use these polynomials on the interval
. In order to use these polynomials on the interval 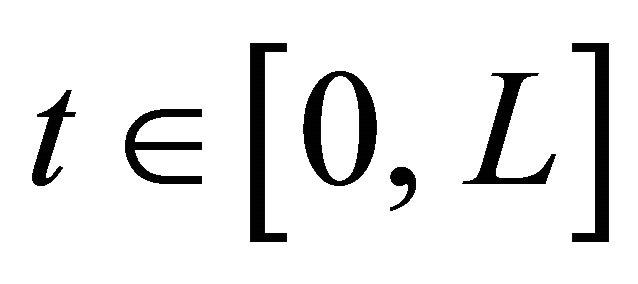 we define the so called shifted Legendre polynomials by introducing the change of variable
we define the so called shifted Legendre polynomials by introducing the change of variable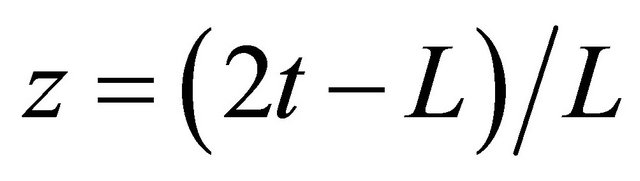 . Let the shifted Legendre polynomials
. Let the shifted Legendre polynomials  be denoted by
be denoted by .
.
Then 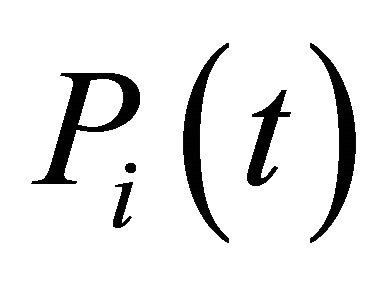 can be obtained as follows:
can be obtained as follows:
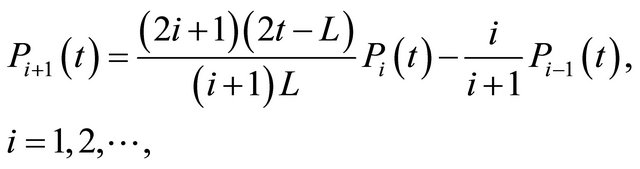 (5)
(5)
where  and
and . The analytic form of the shifted Legendre polynomials
. The analytic form of the shifted Legendre polynomials 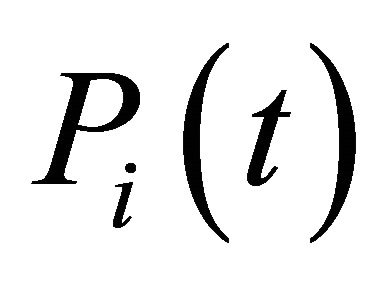 of degree
of degree  given by:
given by:
 (6)
(6)
Note that 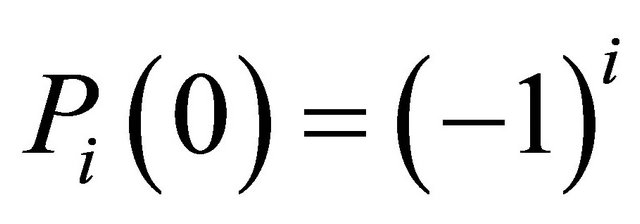 and
and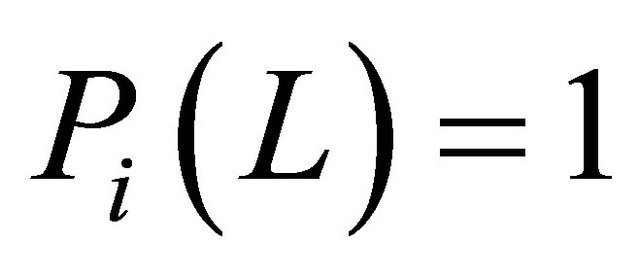 . The orthogonality condition is:
. The orthogonality condition is:
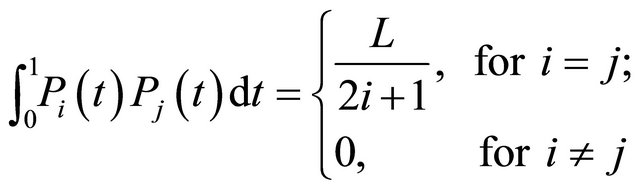 (7)
(7)
The function , square integrable in
, square integrable in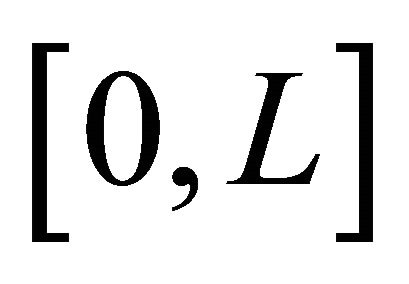 , may be expressed in terms of shifted Legendre polynomials as:
, may be expressed in terms of shifted Legendre polynomials as:
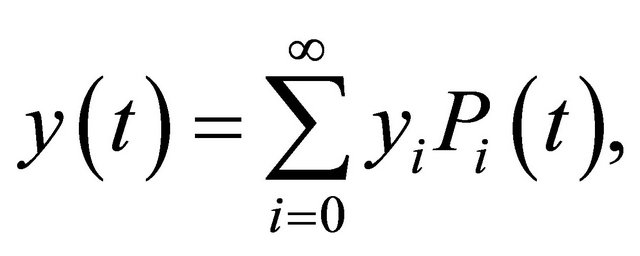 (8)
(8)
where the coefficients 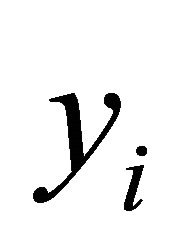 are given by:
are given by:
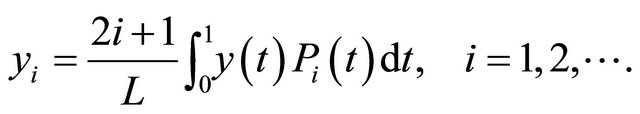 (9)
(9)
In practice, only the first  -terms shifted Legendre polynomials are considered. Then we have:
-terms shifted Legendre polynomials are considered. Then we have:
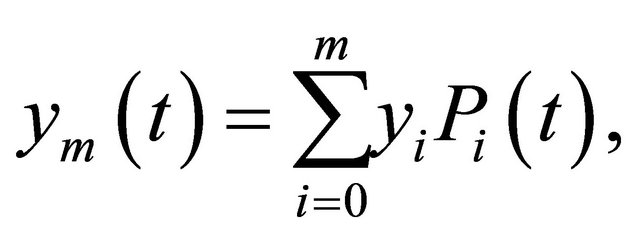 (10)
(10)
In the following theorem we introduce an approximate formula of the fractional derivative of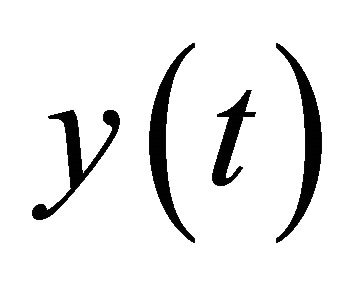 .
.
Theorem 1 Let 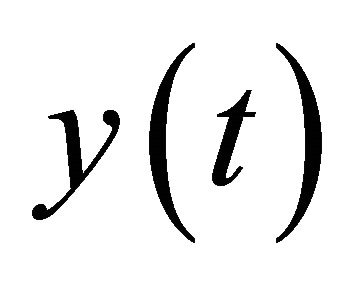 be approximated by shifted Legendre polynomials as (10) and also suppose
be approximated by shifted Legendre polynomials as (10) and also suppose  then:
then:
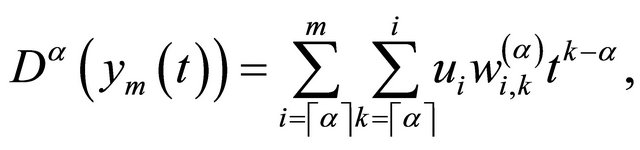 (11)
(11)
where  is given by:
is given by:
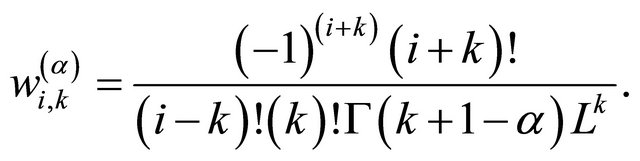 (12)
(12)
Proof. Since the Caputo’s fractional differentiation is a linear operation we have:

Employing Equations (3) in Equation (6) we have:

Also, for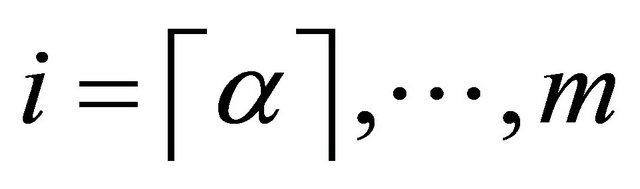 , by using Equations (3) in Equation (6) we get:
, by using Equations (3) in Equation (6) we get:

4. Solution of Multi-Order Fractional Differential Equations
Consider the multi-order fractional differential equations of type given in (13):
 (13)
(13)
with initial conditions:
 (14)
(14)
where ,
, 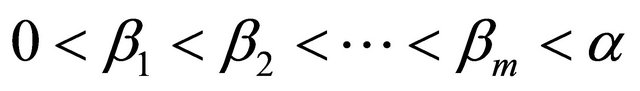 and
and 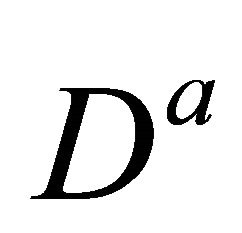 denotes the Caputo fractional derivative of order a. It should be noted that F can be nonlinear in general. To solve problems (13) and (14) we approximate
denotes the Caputo fractional derivative of order a. It should be noted that F can be nonlinear in general. To solve problems (13) and (14) we approximate ,
, 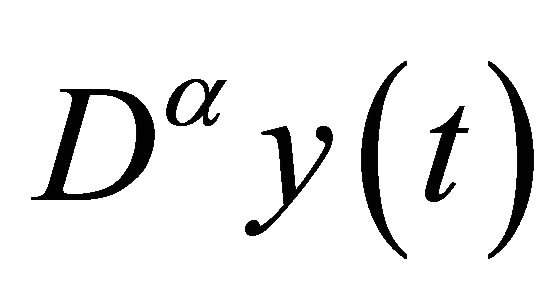 and
and , for
, for  by the shifted Legendre polynomials.
by the shifted Legendre polynomials.
In order to use Legendre pseudo-spectral method, we first approximate  as:
as:
 (15)
(15)
From (13), (15) and Theorem 1, we have:
 (16)
(16)
we now collocate (16) at 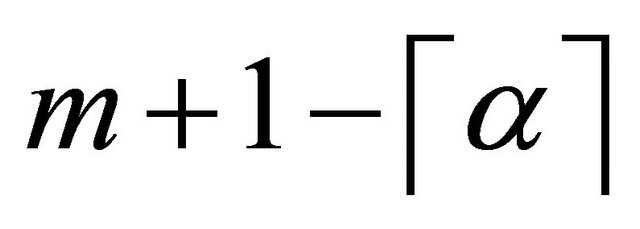 points
points  as:
as:
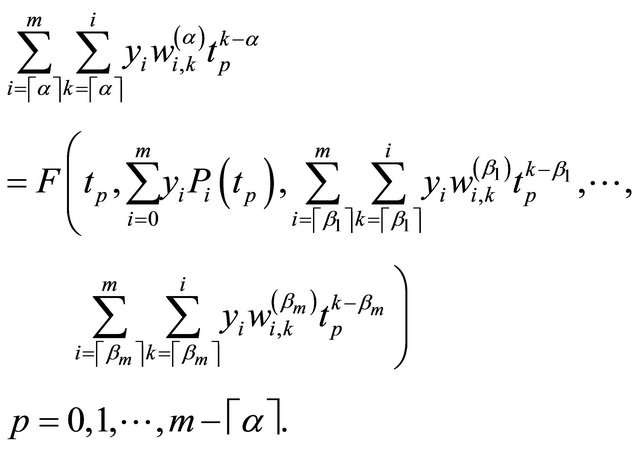 (17)
(17)
For suitable collocation points tp, we use  roots of shifted Legendre polynomial
roots of shifted Legendre polynomial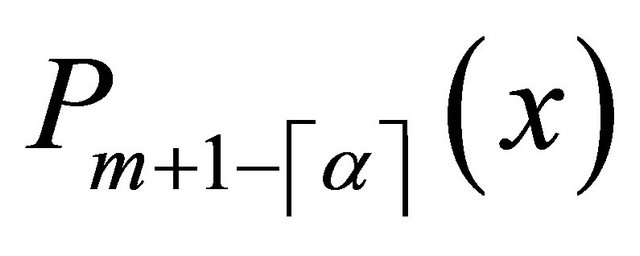 .
.
Also, by substituting (15) in the initial conditions (14) we can obtain  equations as follows:
equations as follows:
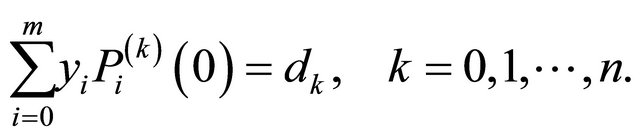 (18)
(18)
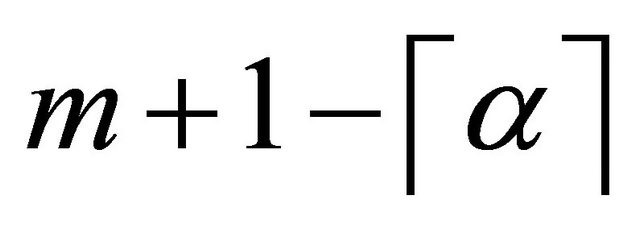 equations in (17) together with
equations in (17) together with  equations of the boundary conditions (18), generate
equations of the boundary conditions (18), generate  equations which can be solved using Newton’s iterative method for the unknown
equations which can be solved using Newton’s iterative method for the unknown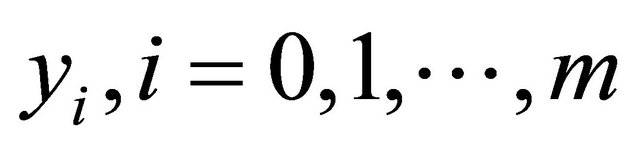 . Consequently
. Consequently  can be calculated.
can be calculated.
5. Numerical Examples
In this section, we will use the Legendre collocation method to solve nonlinear fractional (arbitrary) order differential equation. These examples are considered because closed form solutions are available for them, or they have also been solved using other numerical schemes. This allows one to compare the results obtained using this scheme with the analytical solution or the solutions obtained using other schemes.
Example 1. Consider the following initial value problem
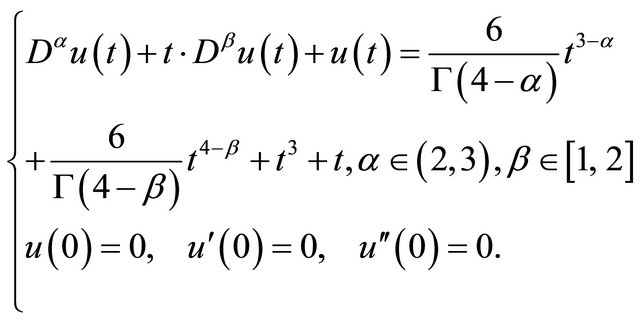 (19)
(19)
If we take ,
,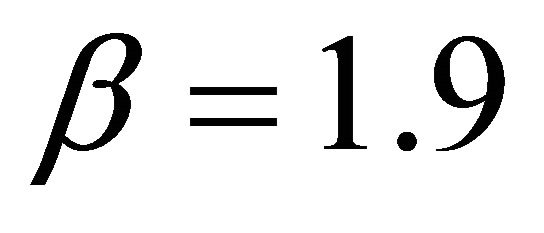 , the exact solution of (19) is
, the exact solution of (19) is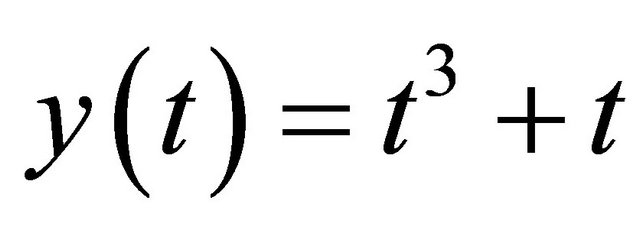 .
.
To solve the above problem, by applying the technique described in last section with m = 4, we get

Then the approximate solution will be
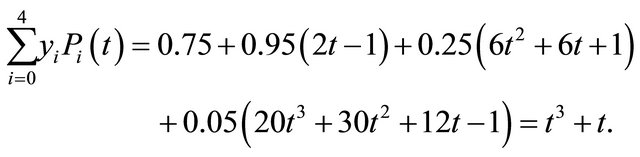
It is clear that the approximate solution coincides with the analytic solution.
Example 2. Consider the following nonlinear differential equation:
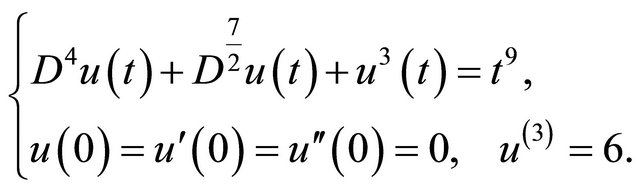 (20)
(20)
The exact solution of (20) is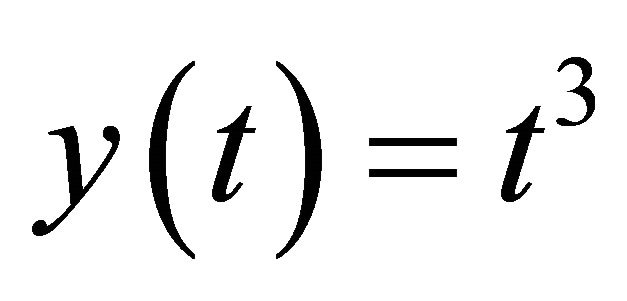 .
.
We use the Legendre pseudo-spectral method with  to obtain 4
to obtain 4
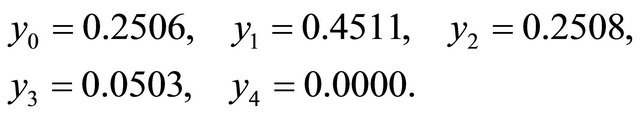
Then the approximate solution will be
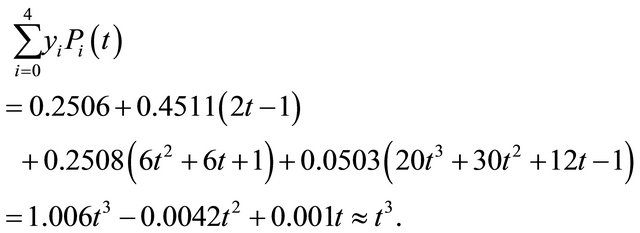
My result is in good agreement with exact solution. This demonstrates the importance of my numerical scheme in solving nonlinear multi-order fractional differential equations.
Example 3. Following Odibat and Momani [6], we consider fractional Riccati equation
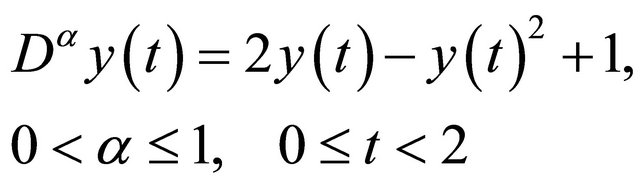 (21)
(21)
subject to the initial state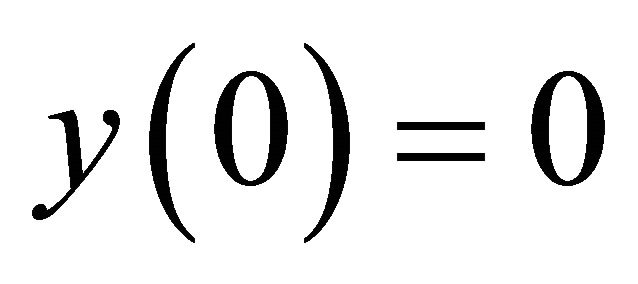 , which is studied by Odibat [6] by using the modified homotopy perturbation method and Li [10] by using the Chebyshev wavelet operational matrices method. Here we use the Legendre pseudo-spectral method to solve it.
, which is studied by Odibat [6] by using the modified homotopy perturbation method and Li [10] by using the Chebyshev wavelet operational matrices method. Here we use the Legendre pseudo-spectral method to solve it.
This is a nonlinear system of algebraic equations. The numerical solution, for m = 8, is shown in Figure 1. The exact solution of this problem, when , is
, is
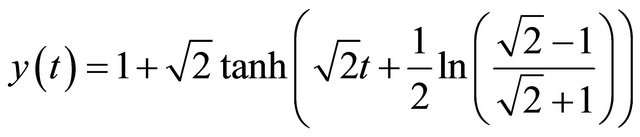
and we can observe that, as ,
,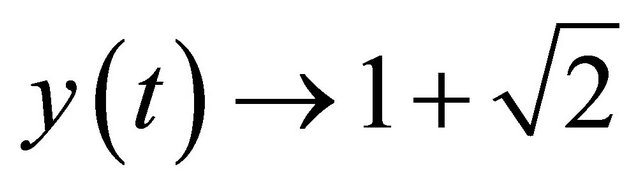 . From Figure 1 we can see the numerical solution is very good agreement with the exact solution when
. From Figure 1 we can see the numerical solution is very good agreement with the exact solution when . When
. When  and
and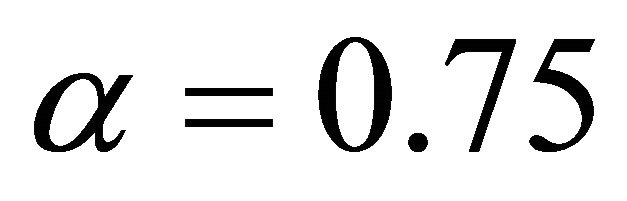 , the numerical solution is very good agreement with the result in Ref. [10]. Therefore, we hold that the solution for
, the numerical solution is very good agreement with the result in Ref. [10]. Therefore, we hold that the solution for 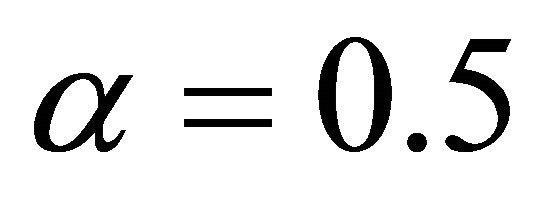 and
and 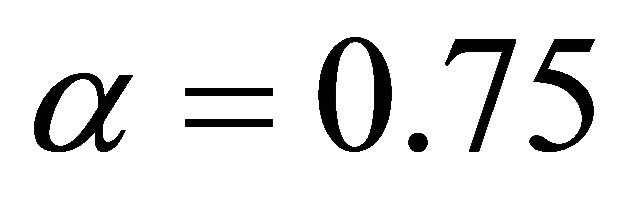 is also credible. Numerical results with comparison to Ref. [6] and [10] are given in Table 1 on the interval
is also credible. Numerical results with comparison to Ref. [6] and [10] are given in Table 1 on the interval .
.
The difference between our result or in Ref. [10] and the result in Ref. [6] is obvious. Because only the fourth-order term of the homotopy perturbation solution were used in evaluating the approximate solutions in Ref. [6]. We hold that our results are better for  and
and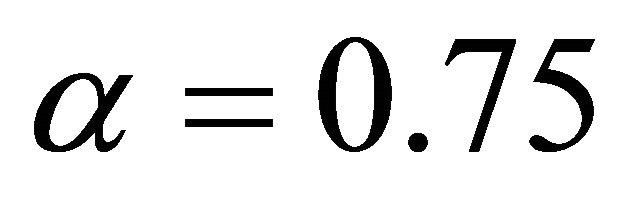 . Compared to the Chebyshev wavelet operational matrices method in Ref. [10] with 192 degrees of freedom, our method reached the same accuracy used 9 degrees of freedom only.
. Compared to the Chebyshev wavelet operational matrices method in Ref. [10] with 192 degrees of freedom, our method reached the same accuracy used 9 degrees of freedom only.
6. Conclusion
Fractional calculus has been used to model physical and engineering processes that are found to be best described by fractional differential equations. For that reason we need a reliable and efficient technique for the solution of

Figure 1. The behavior of the exact and approximate solution of example with 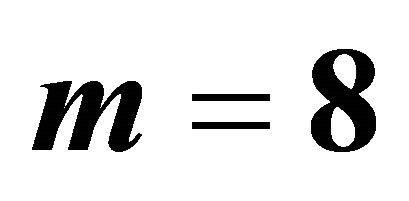 of Example 3.
of Example 3.
Table 1. Numerical results with comparison to Ref. [6] and [10] for Example 3.

fractional differential equations. This paper deals with the approximate solution of a class of multi-order fractional differential equations. The fractional derivatives are described in the Caputo sense. Our main aim is to evaluation of fractional derivative using Legendre polynomials and implementing it to solve the nonlinear multiorder fractional differential equations. The main characteristic behind the approach using this technique is that it reduces such problems to those of solving a system of algebraic equations thus greatly simplifying the problem. Illustrative example is included to demonstrate the validity and applicability of the presented technique. The comparison certifies that our method gives good results.
7. Acknowledgements
This work was partially supported by NSFC Project (Grant No. 11031006, 11126304), the Key Project of Scientific Research Fund of Hunan Provincial Science and Technology Department (Grant No. 2011FJ2011), the Chinese Program for Changjiang Scholars and Innovative Research Team in University (PCSIRT) (Grant No. IRT1179).
REFERENCES
- H. H. Sun, B. Onaral and Y. Tsao, “Application of Positive Reality Principle to Metal Electrode Linear Polarization Phenomena,” IEEE Transactions on Biomedical Engineering, Vol. 31, No. 10, 1984, pp. 664-674. doi:10.1109/TBME.1984.325317
- H. H. Sun, A. A. Abdelwahab and B. Onaral, “Linear Approximation of Transfer Function with a Pole of Fractional Order,” IEEE Transactions on Automatic Control, Vol. 29, No. 5, 1984, pp. 441-444. doi:10.1109/TAC.1984.1103551
- C. Li and G. Chen, “Chaos and Hyperchaos in the Fractional-Order Rossle Equations,” Physica A, Vol. 341, No. 1, 2004, pp. 55-61. doi:10.1016/j.physa.2004.04.113
- N. H. Sweilam, M. M. Khader and R. F. AlffBar, “Numerical Studies for a Multi-Order Fractional Differential Equation,” Physics Letter A, Vol. 371, No. 1-2, 2007, pp. 26-33. doi:10.1016/j.physleta.2007.06.016
- V. S. Erturk, S. Momani and Z. Odibat, “Application of Generalized Differential Transform Method to Multi-Order Fractional Differential Equations,” Communications in Nonlinear Science and Numerical Simulation, Vol. 13, No. 8, 2008, pp. 1642-1654. doi:10.1016/j.cnsns.2007.02.006
- Z. Odibat and S. Momani, “Modified Homotopy Perturbation Method: Application to Quadratic Riccati Differential Equation of Fractional Order,” Chaos, Solitons and Fractals, Vol. 36, No. 1, 2008, pp. 167-174. doi:10.1016/j.chaos.2006.06.041
- Y. Chen and T. Tang, “Convergence Analysis for the Jacobi Collocation Methods to Volterra Integral Equations with a Weakly Singular Kernel,” Mathematics of Computation, Vol. 79, No. 269, 2010, pp. 147-167. doi:10.1090/S0025-5718-09-02269-8
- X. Li and C. Xu, “A Space-Time Spectral Method for the Time Fractional Diffusion Equation,” SIAM Journal on Numerical Analysis, Vol. 47, No. 3, 2009, pp. 2108-2131. doi:10.1137/080718942
- Y. Wei and Y. Chen, “Convergence Analysis of the Legendre Spectral Collocation Methods for Second Order Volterra Integro-Differential Equations,” Numerical Mathematics: Theory, Methods and Applications, Vol. 4, No. 4, 2011, pp. 339-358.
- Y. Li, “Solving a Nonlinear Fractional Differential Equation Using Chebyshev Wavelets,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 9, 2010, pp. 2284-2292. doi:10.1016/j.cnsns.2009.09.020
- V. Gejji and H. Jafari, “Solving a Multi-Order Fractional Differential Equation Using Adomian Decomposition,” Applied Mathematics and Computation, Vol. 189, No. 1, 2007, pp. 541-548.
- S. Yang, A. Xiao and H. Su, “Convergence of the Variational Iteration Method for Solving Multi-Order Fractional Differential Equations,” Computers and Mathematics with Applications, Vol. 60, No. 10, 2010, pp. 2871- 2879. doi:10.1016/j.camwa.2010.09.044
- A. El-Mesiry, A. El-Sayed and H. El-Saka, “Numerical Methods for Multi-Term Fractional (Arbitrary) Orders Differential Equations,” Computational and Applied Mathematics, Vol. 160, No. 3, 2005, pp. 683-699. doi:10.1016/j.amc.2003.11.026
- B. Baeumer, M. Kovcs and M. M. Meerschaer, “Numerical Solutions for Fractional Reaction-Diffusion Equations,” Computers and Mathematics with Applications, Vol. 55, No. 10, 2008, pp. 2212-2226. doi:10.1016/j.camwa.2007.11.012
- K. Diethelm and N. Ford, “Multi-Order Fractional Differential Equations and Their Numerical Solution,” Applied Mathematics and Computation, Vol. 154, No. 3, 2004, pp. 621-640. doi:10.1016/S0096-3003(03)00739-2

