ABSTRACT

The main aim of this present note is to establish three new Hermite-Hadamard type integral inequalities for r-convex functions. The three new Hermite-Hadamard type integral inequalities for r-convex functions improve the result of original one by Hölder’s integral inequality, Stolarsky mean and convexity of function.

1. Introduction

The inequalities

, (1.1)

which discovered by C. Hermite and Hadamard for all convex functions 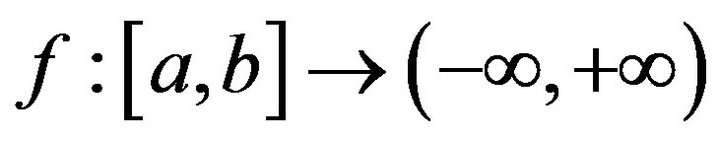are known in the literature as Hermite-Hadamard inequalities.

We note that Hermite-Hadamard inequalities may be regarded as a refinement of the concept of convexity and they follows easily from Jenson’s inequality. HermiteHadamard inequalities for convex functions has received renewed attention in recent years and a remarkable variety of refinements and generalizations have been found in [1-6].

Let 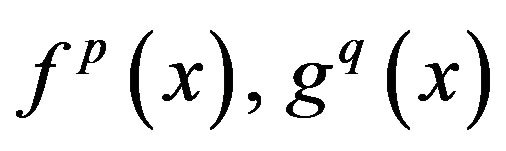be integrable functions on

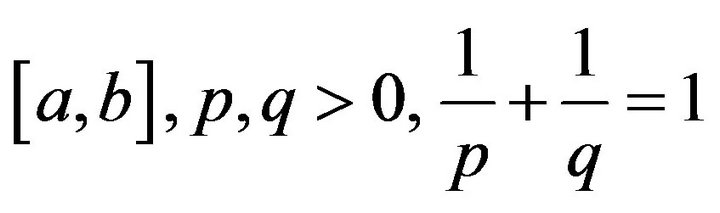then the well known Hölder’s integral inequality is given as

(1.2)

The following definition is well known in the literature.

Definition 1.1. Suppose

.

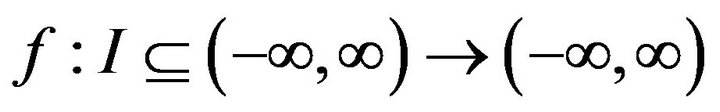If following inequality holds

(1.3)

for any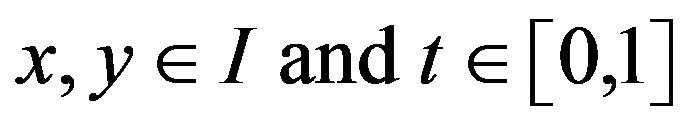, then we say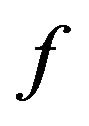is convex function on.

In [1], C. E. M. Pearce, J. Pecaric and V. Simic introduced the definition of -convex function and studied the inequalities of Hermite-Hadamard type for 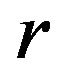-convex functions.

Definition 1.2. ([1]) A function

is said to be 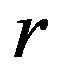-convex function on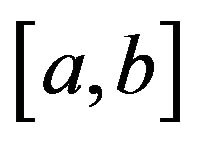, if

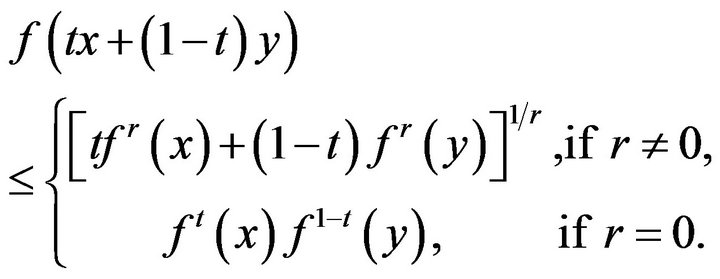(1.4)

holds for any and.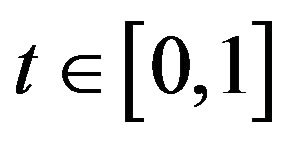

We have that 0-convex functions are simply log-convex functions and 1-convex functions are ordinary convex functions.

The integral power mean 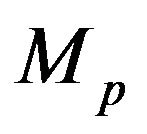(see [2]) of a positive functi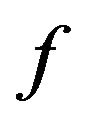on on 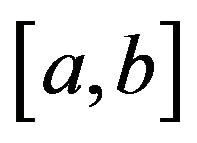is a functional given by

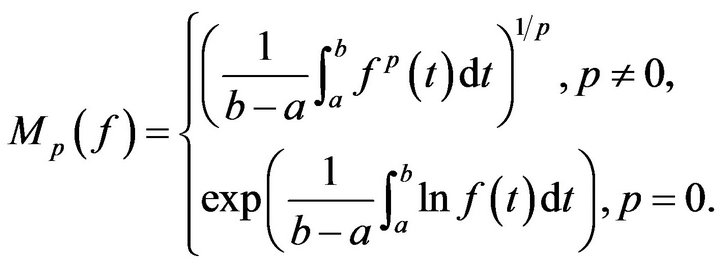(1.5)

The Stolarsky mean (see [7]) of two positive numbers 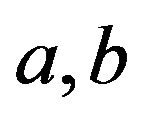is given by

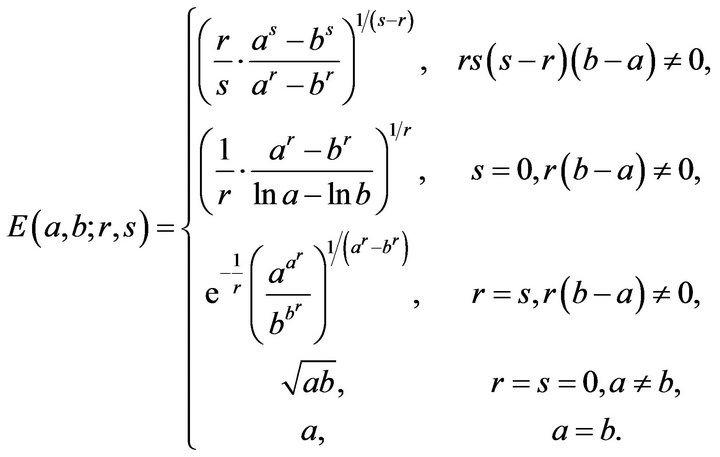(1.6)

In [2], following theorem is given.

Theorem 1.1. ([2]) Let 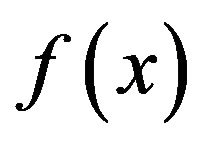be a positive -convex function on and is defined by

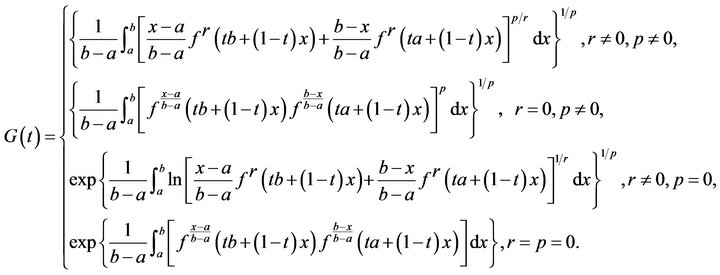(1.7)

Then

(i) 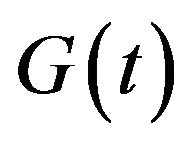is monotonically increasing on;

(ii).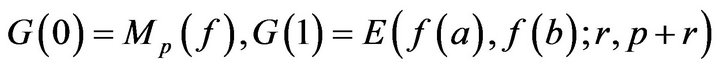

In [4], following theorems are given.

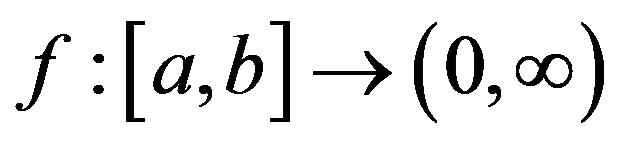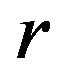Theorem 1.2. ([3]) Letbe-convex function on 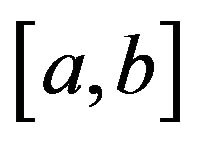with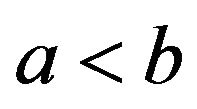. Then the following inequality holds for

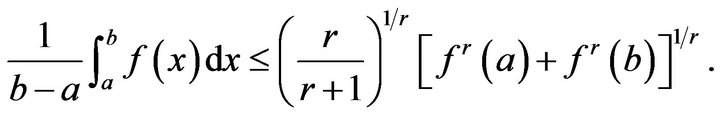
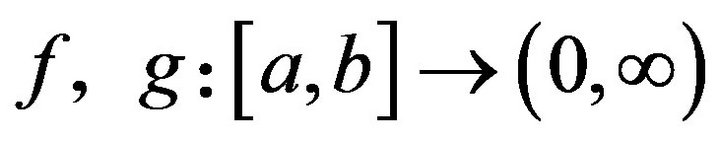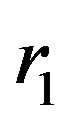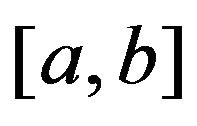Theorem 1.3. ([3]) Let be - convex and -convex functions respectively on with 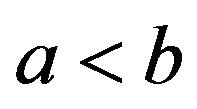Then the following inequality holds for,

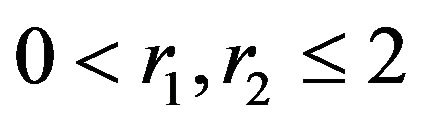Theorem 1.4. ([3]) Let 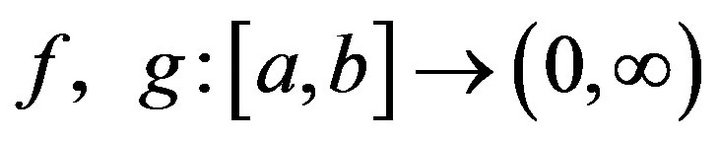be convex and -convex functions respectively on 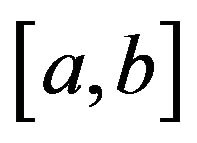with Then the following inequality holds

for 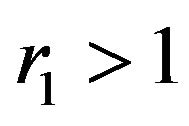and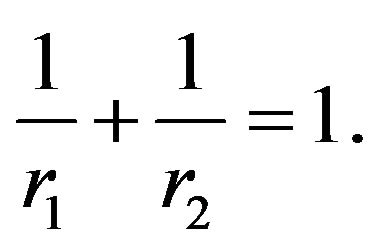

2. Main Results

In this paper we obtain some new Hermite-Hadamard type integral inequalities for 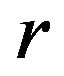-convex functions and improve the results of Theorems 1.2-1.4.

The following are extensions of Hermite-Hadamard type inequality:

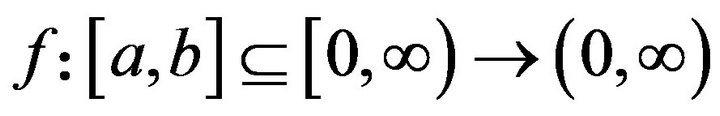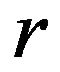Theorem 2.1. Let be - convex function on 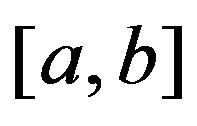with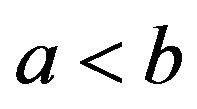,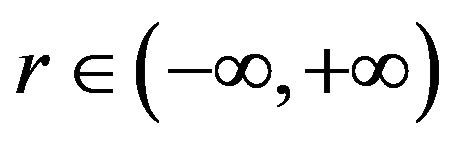. Then

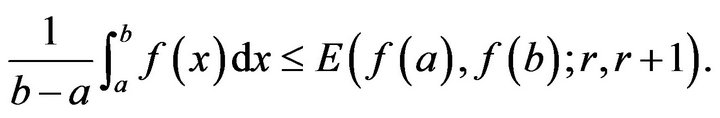(2.1)

Proof. Let, then

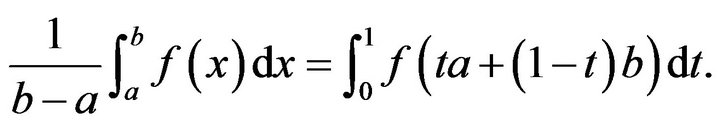
If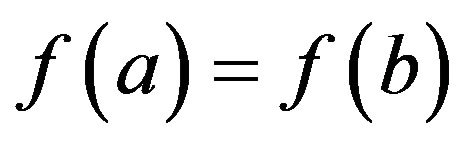, by the 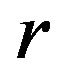-convexity of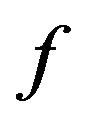, we have

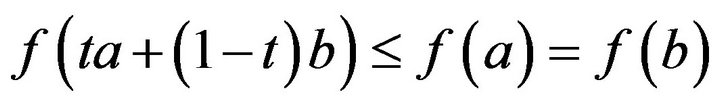
for any 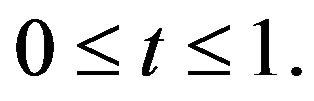So the conclusion is valid.

If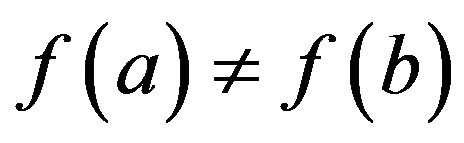, we have to discuss three cases as following:

Case 1. If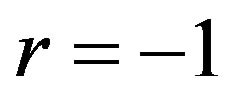, we have

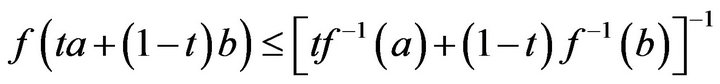
for any Hence, we obtain

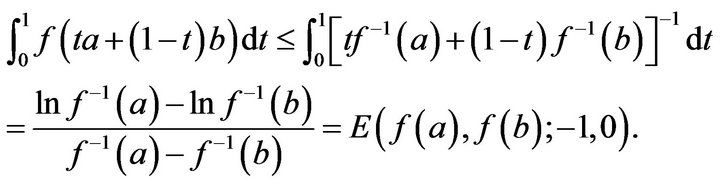
Case 2. If, we have

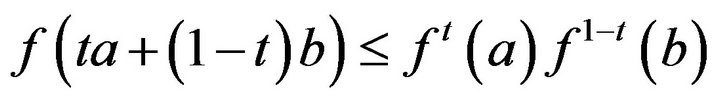
for any 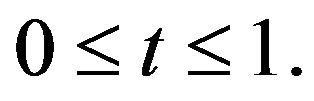Hence, we obtain

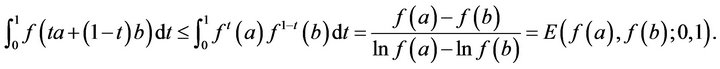
Case 3. If 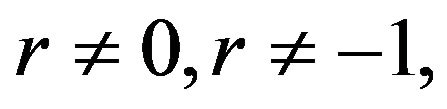we have

for any 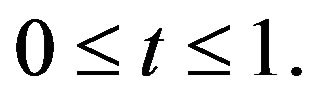Hence, we get

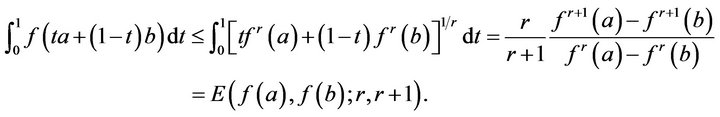
The proof of Theorem 2.1 is complete.

Corollary 2.1.1. If 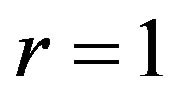in Theorem 2.1, we have

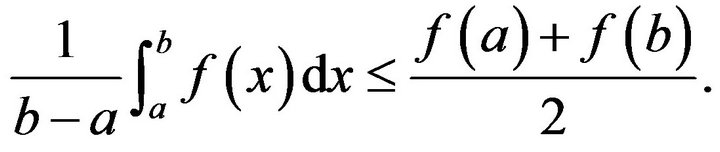(2.2)

Theorem 2.2. Let

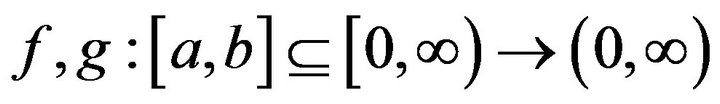
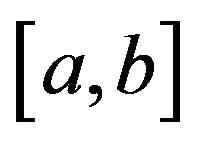be -convex and -convex functions respectively on with 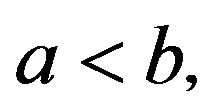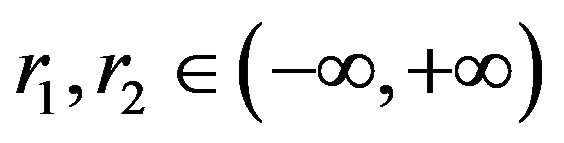. Then the following inequality holds

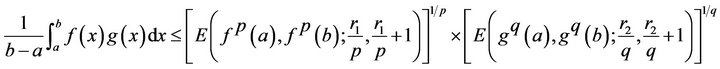(2.3)

for any 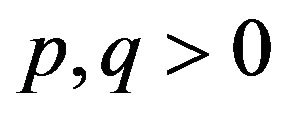and.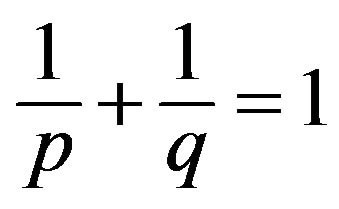

Proof. Let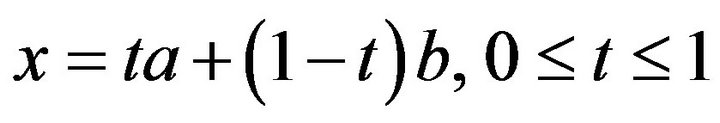, then we have

.

If 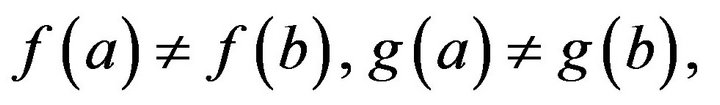then 1) when 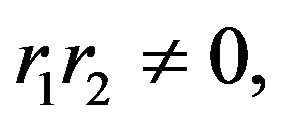by the 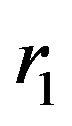-convexity and -convexity of functions 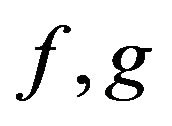respectively, we have

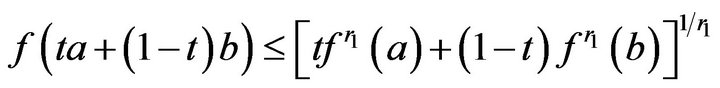
and

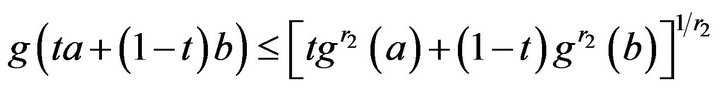
for any 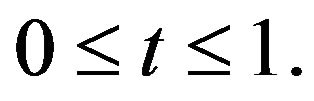So we obtain

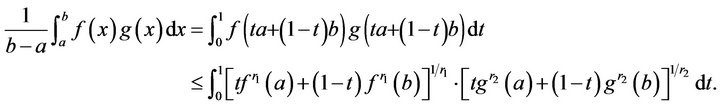
By the Hölder’s integral inequality and Theorem 2.1, we have

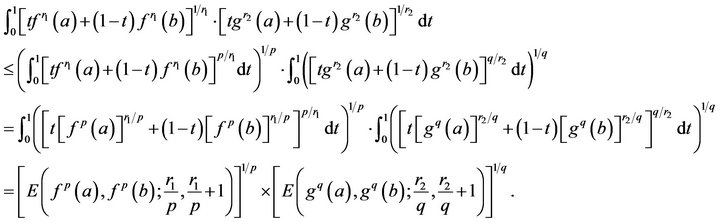
2) when 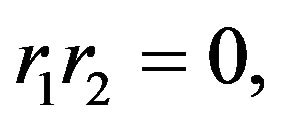we just prove for 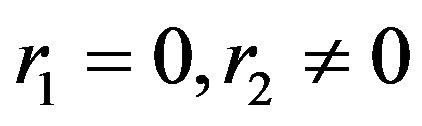which is similar to 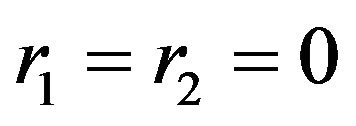and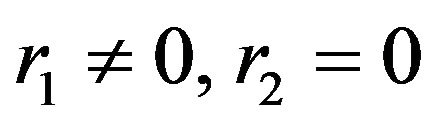. By the Hölder’s integral inequality, Theorem 2.1 and 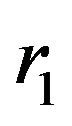-convexity and -convexity of functions 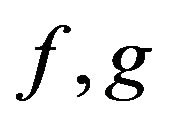respectively, we have

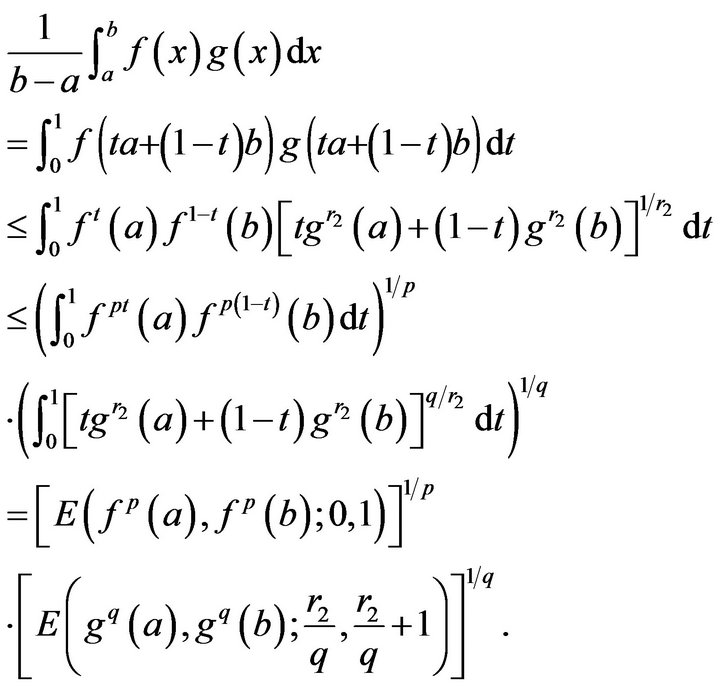
If 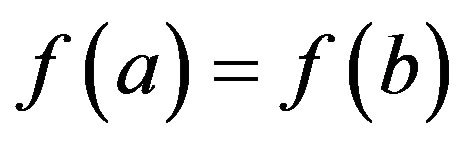or, by Theorem 2.1 we obtain the conclusion, which the proof of Theorem 2.2 is completed.

Corollary 2.2.1. Under the conditions of Theorem 2.2if 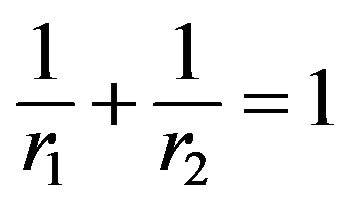for any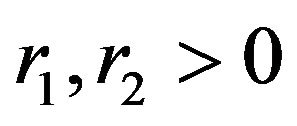, then we have

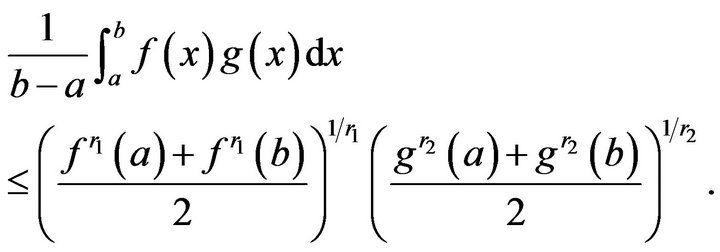(2.4)

In particular, if, then we have

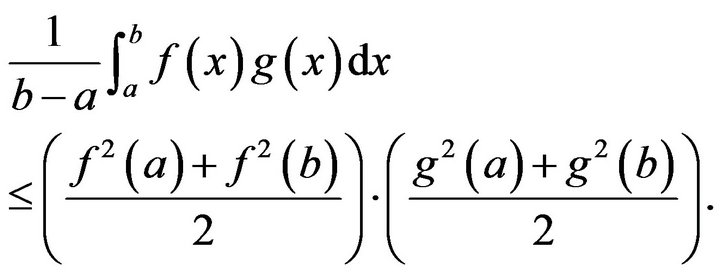
If, , 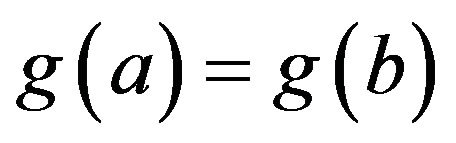we have

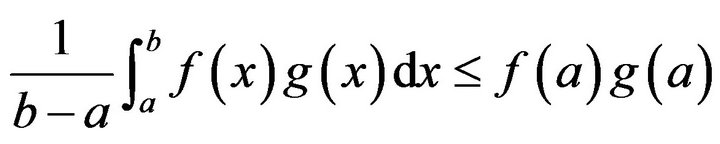
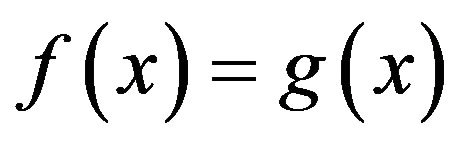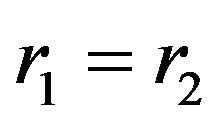Corollary 2.2.2. Under conditions of Theorem 2.2, if and then we have

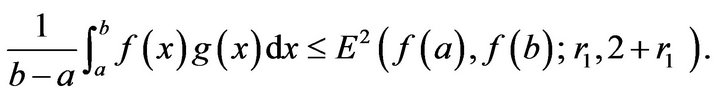(2.5)

In particular, if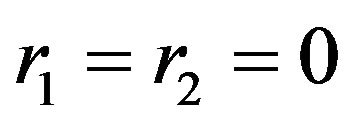, then we have

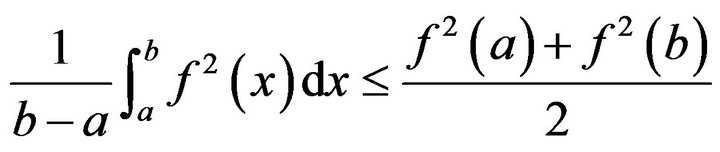
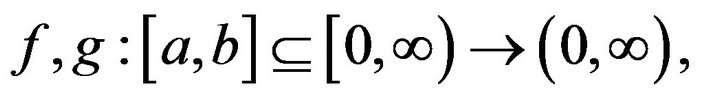
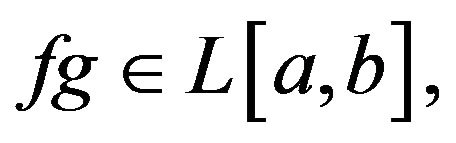
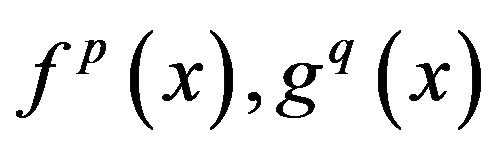Theorem 2.3. Let and be -convex and -convex functions respectively on with 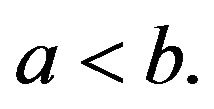Then the following inequality holds

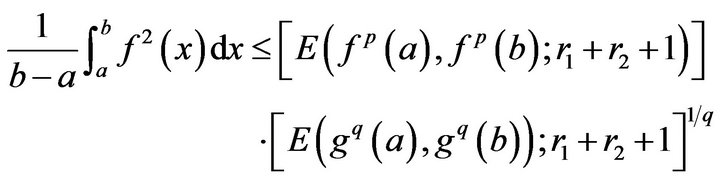(2.6)

for any and.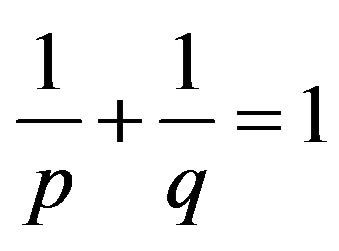

Proof. Let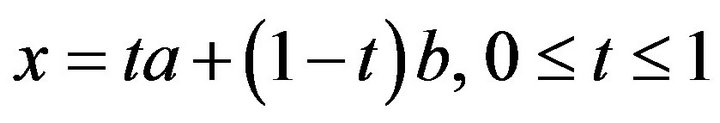, then we have

.

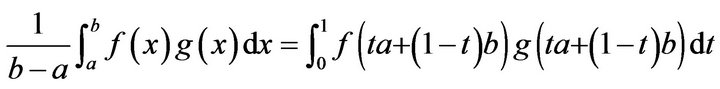By the Hölder’s integral inequality, Theorem 2.1 and 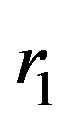-convexity and -convexity of function 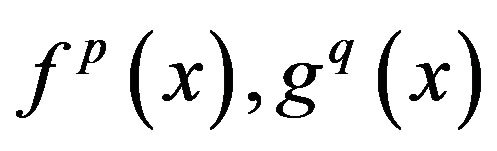respectively, we have

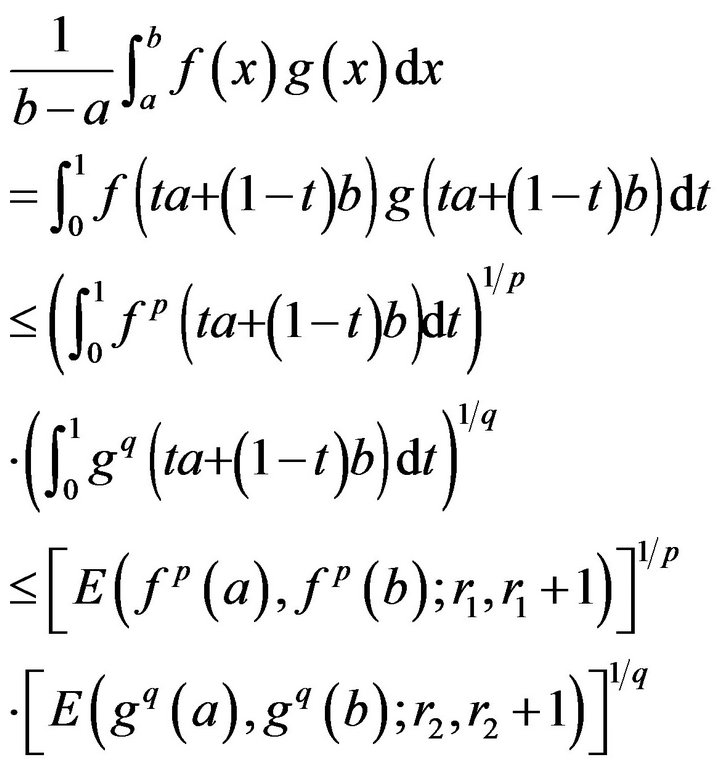
This completed the proof of Theorem 2.3.

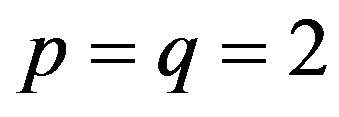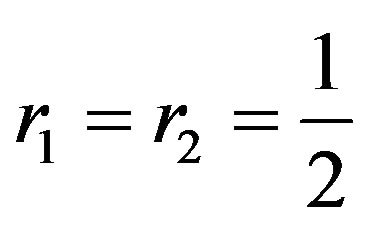Corollary 2.3.1. Under the conditions of Theorem 2.3if and, then we have

(2.7)

In particular, if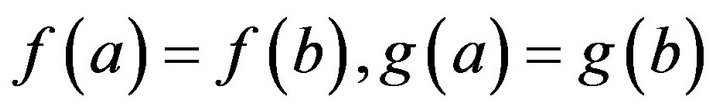, we have

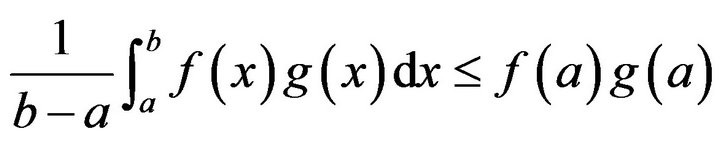
In this paper, we obtained three new Hermite-Hadamard type integral inequalities for 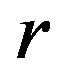-convex functions, which improved the results of Theorems 1.2-1.4 by Hölder’s integral inequality, Stolarsky mean and convexity of function. The special case of new Hermite-Hadamard type integral inequalities is classical Hermite-Hadamard type integral inequality. So it improved the classical one.

3. Acknowledgements

The first author was supported in part by the National Natural Science Foundation of China under Grant No. 11161033 and Inner Mongolia Natural Science of China under Grant No. 2010MS0119.

REFERENCES