Applied Mathematics
Vol.3 No.9(2012), Article ID:23021,5 pages DOI:10.4236/am.2012.39161
A New Fuzzy Control Model for Kidney Patients
1Department of Applied Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran
2Department of Nephrology, Ghaem Hospital, Mashhad, Iran
Email: math.lagzian64@gmail.com, shirazian65@yahoo.com
Received June 13, 2012; revised August 16, 2012; accepted August 23, 2012
Keywords: Mathematical Modeling; Fuzzy Control Model; Kidney Transplantation; Membership Functions
ABSTRACT
The final diagnosis of some diseases depends on many factors and information. Considering all these factors and reviewing all of them is a difficult process, thus providing a mathematical model that can simultaneously consider all these factors is a great help for physicians to diagnose and treat these diseases. In this paper, we propose a new fuzzy control model for kidney transplantation patients. For the inference and conclusion of this model, we use Mamdani approach. Also we employ a new method to smooth the well-known non-smooth piecewise membership functions, i.e. trapezoidal and half trapezoidal membership functions.
1. Introduction
There are many papers about mathematical applications in medical field. These papers usually tried to propose mathematical models to control diseases, adjusting the optimal dosage of medicine to the better treatment of disease and etc. As we know, one of the most important and vital organs inside the human body are kidneys, which are responsible for blood filtration. If this organ doesn’t work properly, it can cause many problems for the body and even the human die. One way to treat kidney failures is kidney transplantation. Before the kidney transplantation, it is important to know whether the human body will accept the graft or will reject it, or whether the graft will work well or not. If one can predict them by data obtained from the previous patients under kidney transplantation, it can improve the confidence of physicians to do the transplanting or not.
In this paper we propose a mathematical model to determine whether patient’s transplanted kidney will work well or not, in the first week after transplantation, or it has delay in the function using provided medical information, before transplantation. Since medical concepts are not clear and there is no transparent and complete finality in medical issues, the fuzzy logic has been used to propose this model.
To design this fuzzy control system, the most important factors that regarding medical treats and articles, physician’s decisions, they can affect the results of kidney transplantation are gender, insulin resistance, age and so on. Categorizing each of these factors, we offer the fuzzy control rules as “IF-THEN”. After determining these rules, which are the basis of the fuzzy control model, we exert the inputs (indices) that are related to a patient who has been selected for kidney transplantation, to the system of fuzzy rules and then we use one of the defuzzification methods to the final conclusions according to the Mamdani approach. That is, we specify that the kidney transplanted to the patient, will works well or patient will have delayed graft function.
2. The Main Factors or Variables in Kidney Transplantation
In this section, we consider some indicators or factors that are considered to have effect on patient’s kidney transplantation. Then we divide each of these factors for use in the fuzzy control model to the better classification of patients. Some of the most important factors in the kidney transplantation are gender, insulin resistance, kind of donor, (alive or cadaver), impaired pancreatic beta cell or beta cell function, BMI, length of dialysis before transplantation, systolic and diastolic blood pressure before and after the transplantation.
Considering these factors, first we classify them according to their gender. Then each of the above-mentioned groups is divided into two groups according to transplanted kidney is taken from alive or cadaver. Other factors are classified as follows:
2.1. Insulin Resistance Factor
With regards to the expert’s sight, if insulin resistance’s measure is less than one, a body hasn’t insulin resistance. Otherwise the body has insulin resistance. If patient’s insulin resistance is 0.999 and for other patient is 1.001, can we conclude that the first patient has insulin resistance and the other one hasn’t? It seems that it isn’t a true conclusion. For solving this mistake and having more clearly and closely conclusion, with regards to expert’s point of view, we propose a fuzzy function for insulin resistance factor. Now, when we want to response a question about has patient's body have insulin resistance or not, the answer is what membership degree of insulin resistance has the patient’s body. Figure 1 shows the membership function of this factor.
2.2. Impaired Pancreatic Beta Cells
In the case of does patient’s body have an impaired pancreatic beta cell or not, we do the same as insulin resistance factor. It means that we explain the value of impaired pancreatic beta cell by its membership degree. Figure 2 shows the membership function of this factor:
We explain other factors as the same as 1 and 2, with fuzzy membership functions except that these factors have more than one membership function (Table 1). Figures 3-5, show their membership functions.
2.3. Systolic and Diastolic Pressure
Normal (N): Less than 120 and less than 80.
Slightly high (SH): 120 - 139 or 80 - 89.
High (H): 140 - 159 or 90 - 99.
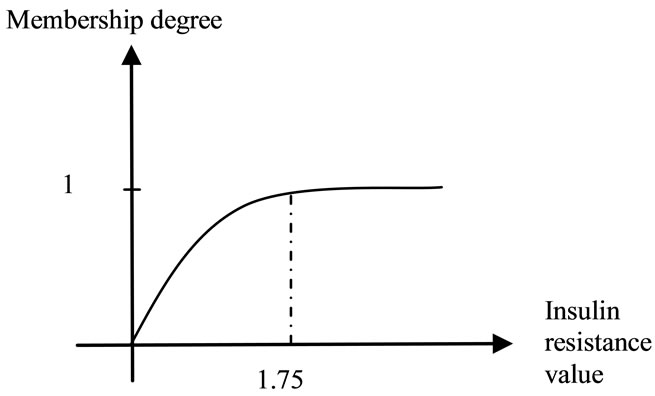
Figure 1. Insulin resistance membership function.
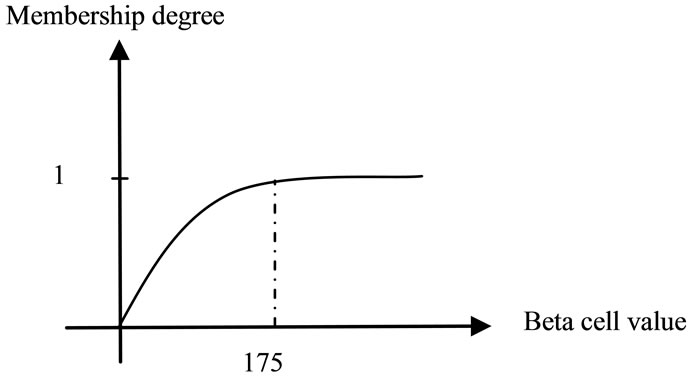
Figure 2. Membership function of beta cell function.

Table 1. Some of the main factors for transplantation with their classifications.
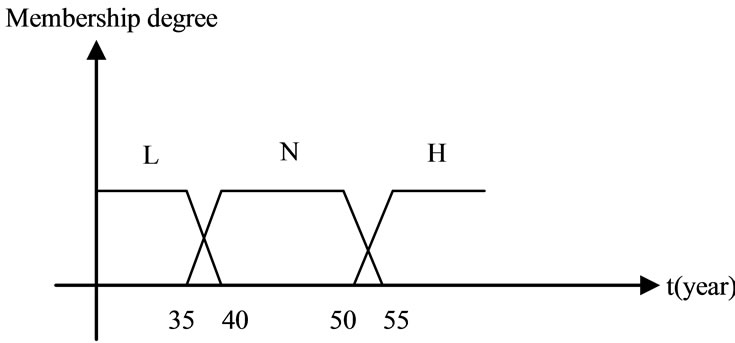
Figure 3. Age membership functions.

Figure 4. BMI membership functions.
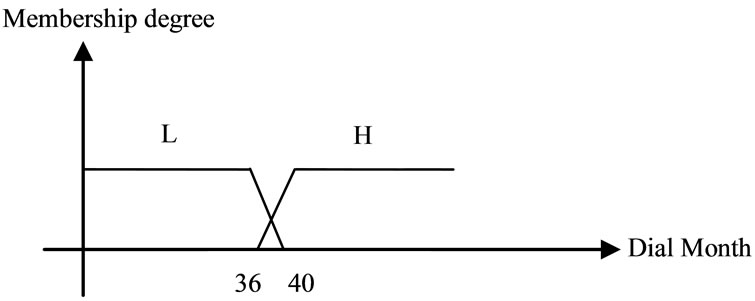
Figure 5. Dial month membership functions.
Very high (VH): Greater than or equal to 160 or 100.
According to the physicians’ sight about the patient’s blood pressure, since the normal case has been considered as “and” and the other cases as “or”, we use the product and maximum of membership degrees, respectively. The corresponding membership functions are depicted in Figures 6 and 7.
3. Approximation of Classical Membership Functions by Smooth Membership Functions
As we know, membership functions play a key role in fuzzy control method. On the other hand, working with
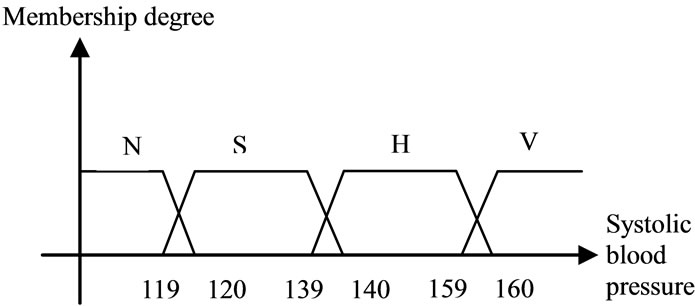
Figure 6. Systolic blood pressure membership function.
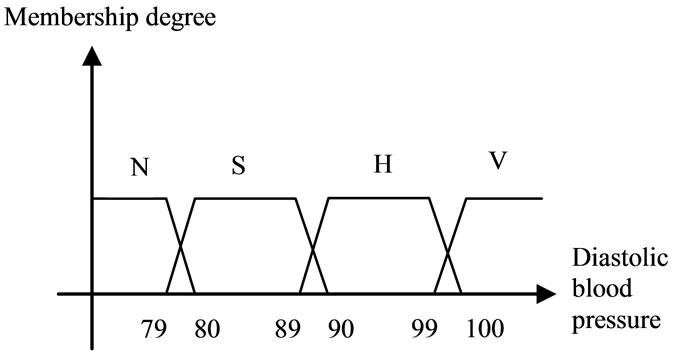
Figure 7. Diastolic blood pressure membership function.
smooth functions, for the reason of applying t-norm and s-norm operators, especially in Mamdani control is much easier than working with several criterion functions and classical piecewise linear ones. Therefore, in this section we smooth all of the membership functions shown in Figures 3-7.
For this purpose, we use the method presented in [1], that implemented the stochastic and goal fuzzy programming. In this method, each fuzzy membership function in the form of triangular, trapezoidal and half trapezoidal can be approximated by the smooth function in general form. We show 3 of these diagrams in Figures 8-10 which are approximated smooth functions of age membership function shown in Figure 3:

where  is a polynomial Here, for example, the age (low, normal and high) membership functions obtained as follows:
is a polynomial Here, for example, the age (low, normal and high) membership functions obtained as follows:
Low age:
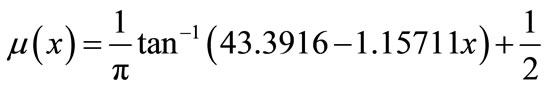
Normal age:
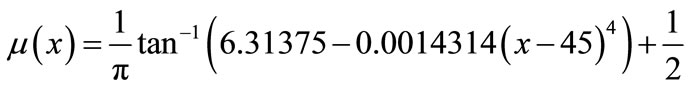
High age:
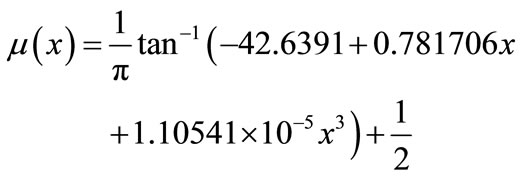

Figure 8. Very high age membership function.
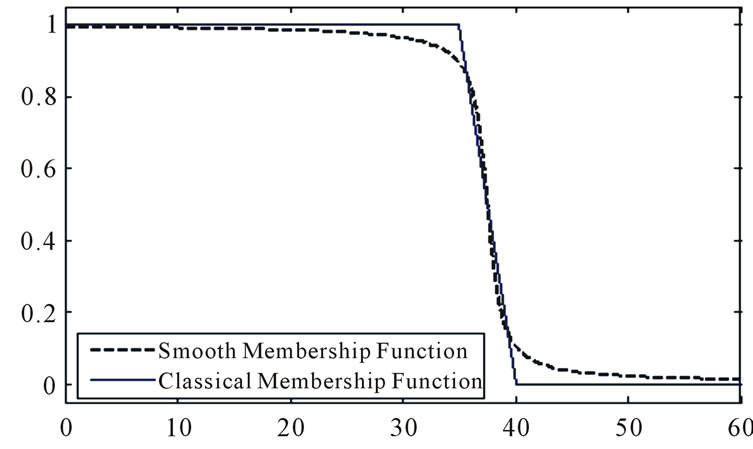
Figure 9. Low age membership function.
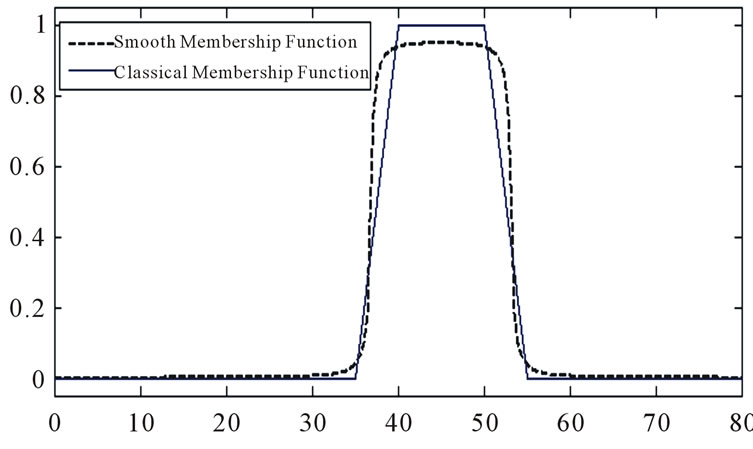
Figure 10. Normal age membership function.
4. Proposed Fuzzy Control System and Basic Rules
Fuzzy reasoning requires some basic rules (inference rules) which can be designed according to expert’s decision. Designing these basic rules that are in the form of “if-then”, the remained steps will be as follows:
1) Determine membership degree in antecedent of each rule;
2) Calculate consequence of rules;
3) Aggregate consequence of rules.
Before explaining the appropriate IF-THEN rules, it is important to mention that the utilized inference procedure is Mamdani method. The main idea of Mamdani control system is explanation of process cases by linguistic variables and demonstrating them with triangular or trapezoidal fuzzy sets.
For example, we can take into consideration the age linguistic variable as low, medium (normal) and high terms. Then by the method mentioned in Section 2, we could change these linguistic variables into fuzzy sets (membership functions) and then change them into smooth membership functions by the method presented in Section 3. In general, the rules that connect the input variables to output variables, are in the following form:
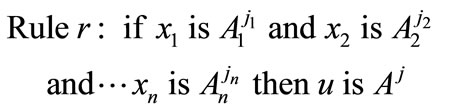
where, 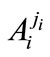 is j-th term of i-th linguistic variable, corresponding to membership function
is j-th term of i-th linguistic variable, corresponding to membership function 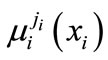 and
and 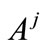 is the output which determines whether the patient’s kidney transplantation has been delayed or not. In the sequel, a table of fifteen fuzzy rules have been used in this article is given For example, the first rule of Table 2 is explained as follows:
is the output which determines whether the patient’s kidney transplantation has been delayed or not. In the sequel, a table of fifteen fuzzy rules have been used in this article is given For example, the first rule of Table 2 is explained as follows:
If age is normal, BMI is low, dial month is low, blood pressure is very high before transplantation and high after transplantation, then the graft has been delayed.
For using the Mamdani control method, it is required for output or “THEN” section to only takes values 0 and 1. We considered this membership function in the following form:
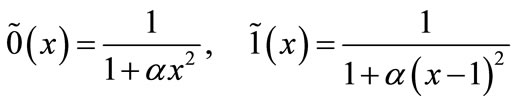
where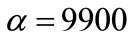 . But the first step in fuzzy control models is calculation of antecedent membership value. Min operator is used for a sample of “and”. Because of product operator having compensation property, we use this operator instead of min operator. r’m rule’s value is calculated as follows:
. But the first step in fuzzy control models is calculation of antecedent membership value. Min operator is used for a sample of “and”. Because of product operator having compensation property, we use this operator instead of min operator. r’m rule’s value is calculated as follows:
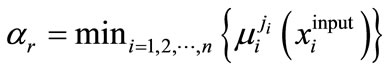
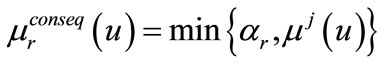
The result of this process, is obtained by aggregation of all results using max operator:
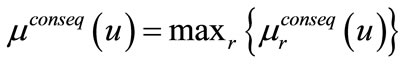
Since the conclusion must give a certain value, 0 or 1, i.e. the graft has been delayed or not, we require one of the adequate defuzzification procedures. Here the center of area (COA) defuzzification method has been employed for conclusion, that is:
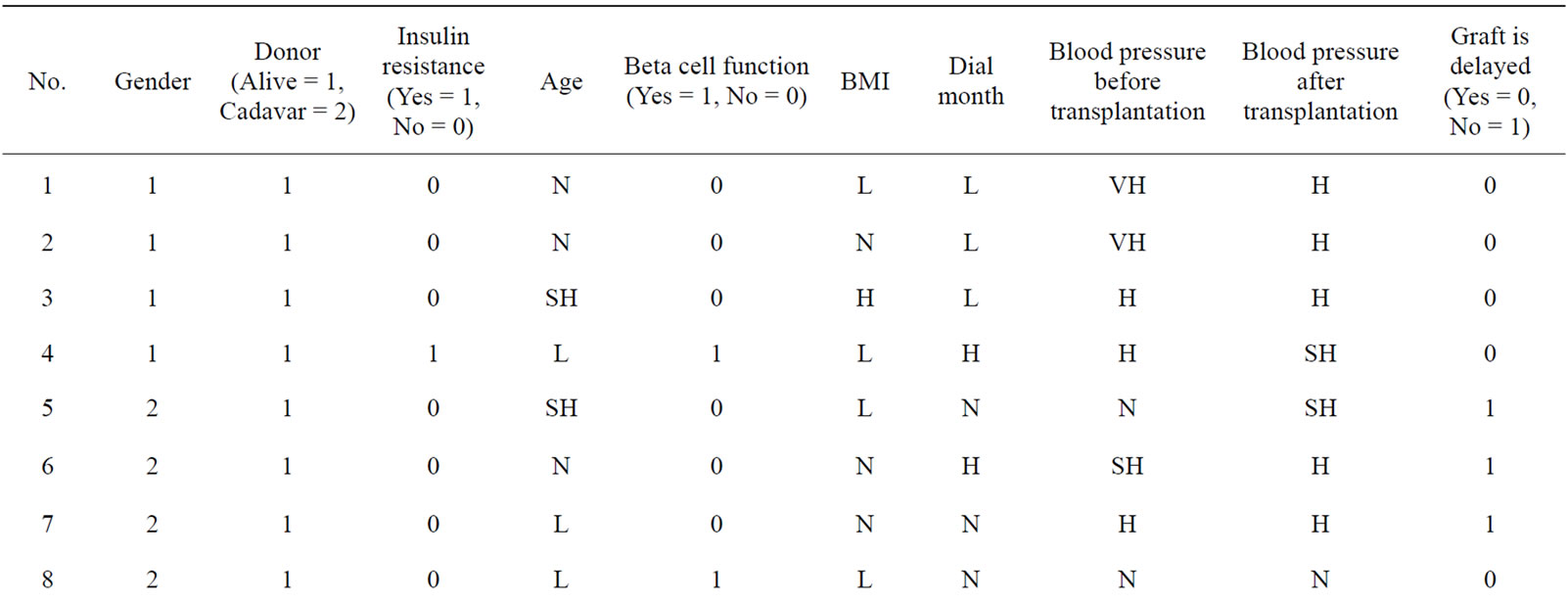
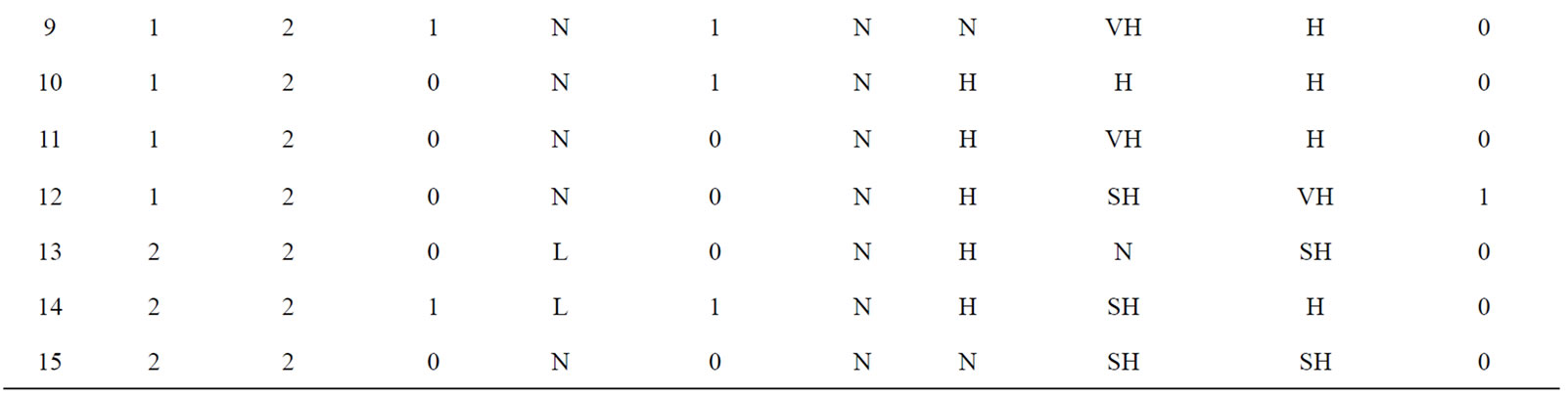
Table 2. Some of the rule bases employed in the proposed method.

Table 3. Simulation results of the proposed method for five patients.
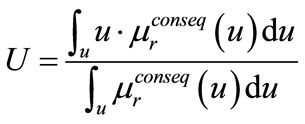
if U is close to zero, it is considered as zero, and if it is close to 1, it is considered as 1. The simulation results which were done by MATLAB software approved the accuracy of the proposed model. In fact, using medical data obtained from some new patients who were undergoing kidney transplantation, the simulations show the consistent of 90 percent of cases with the medical test results. The simulation results are given in Table 3, for five patients.
5. Conclusion
In this paper, according to medical data obtained from patients undergoing kidney transplantation, fuzzy rules have been written and Mamdani fuzzy control model is presented to determine renal function is delayed or not. This result which is given by zero or one is used to raise confidence of medical doctors for transplantation. Accuracy of the proposed model is approved using medical data obtained from some new patients who were undergoing kidney transplantation. For future works, one can predict the fasting blood glucose using the indicators mentioned in this paper.
6. Acknowledgements
This research was supported by a grant from Ferdowsi University of Mashhad, No. MA87149KAM. Also, we appreciate the center of excellence modeling of linear and non-linear systems of department of applied mathematics of Ferdowsi University of Mashhad for their support to achieve this research.
REFERENCES
- A. V. Kamyad, N. Hassan Zadeh and J. Chaji, “An Efficient Approach for Solving a Wide Class of Fuzzy Linear Programming Problems,” International Conference on Computational Intelligence and Software Engineering, Wuhan, 11-13 December 2009.

