ABSTRACT

In this note, it is proved that if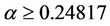, then any digraph on n vertices with minimum outdegree at least 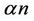contains a directed cycle of length at most 5.

1. Introduction

Let 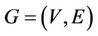be a digragh without loops or parallel edges, where 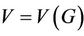is the vertex-set and is the arc-set. In 1978, Caccetta and Häggkvist [1] made the following conjecture:

Conjecture 1.1 Any digraph on n vertices with minimum outdegree at least r contains a directed cycle of length at most.

Trivially, this conjecture is true for, and it has been proved for 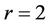by Caccetta and Häggkvist [1], 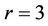by Hamildoune [2], 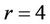and 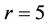by Hoáng and Reed [3], 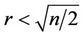by Shen [4]. While the general conjecture is still open, some weaker statements have been obtained. A summary of results and problems related to the Caccetta-Häggkvist conjecture sees Sullivan [5].

For the conjecture, the case 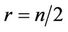is trivial, the case has received much attention, but this special case is still open. To prove the conjecture, one may seek as small a constant 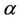as possible such that any digraph on n vertices with minimum outdegree at least 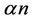contains a directed triangle. The conjecture is that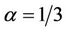. Caccetta and Häggkvist [1] obtained

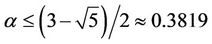, Bondy [6] showed 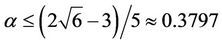, Shen [7] gave

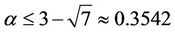, Hamburger, Haxell, and Kostochka [8] improved it to 0.35312. Hladký, Král’ and Norin [9] further improved this bound to 0.3465. Namely, any digraph on n vertices with minimum out-degree at least 0.3465n contains a directed triangle. Very recently, Lichiardopol [10] showed that for, any digraph on n vertices with both minimum out-degree and minimum in-degree at least 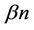contains a cycle of length at most 3.

In this note, we consider the minimum constant 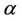such that any digraph on n vertices with minimum outdegree at least 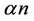contains a directed cycle of length at most 5. The conjecture is that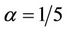. By refining the combinatorial techniques in [6,7,11], we prove the following result.

Theorem 1.2 If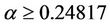, then any digraph on n vertices with minimum outdegree at least contains a directed cycle of length at most 5.

2. Proof of Theorem 1.2

We prove Theorem 1.2 by induction on n. The theorem holds for 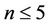clearly. Now assume that the theorem holds for all digraphs with fewer than n vertices for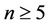. Let G be a digraph on n vertices with minimum outdegree at least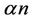. Suppose G contains no directed cycles with length at most 5. We can, without loss of generality, suppose that G is r-outregular, where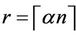, that is, every vertex is of the outdegree r in G. We will try to deduce a contradiction. First we present some notations following [7].

For any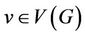, let and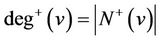, the outdegree of;

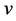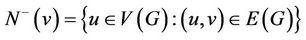and, the indegree of.

We say a transitive triangle if . The arc 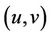is called the base of the transitive triangle.

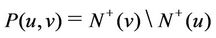For any, let and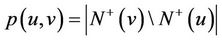, the number of induced 2-path with the first arc;

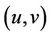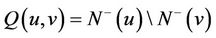and, the number of induced 2-path with the last arc;

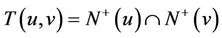and, the number of transitive triangles with base.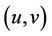

Lemma 2.1 For any,

(1)

Proof: To prove this inequality, we consider two cases according to or.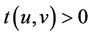

If, then substituting it into (1) yields

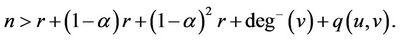(2)

There exists some 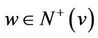with outdegree less than 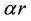in the subdigraph of G induced by 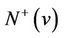(Otherwise, this subdigraph would contain a directed 4-cycle by the induction hypothesis). Thus

.

Consider the subdigraph of G induced by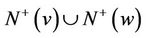, by the induction hypothesis, some vertex 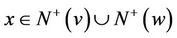has outdegree less than 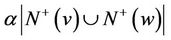in this subdigraph. Thus, the set of outneighbors of x not in satisfies

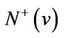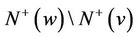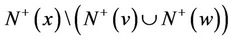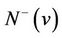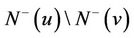Since has no directed 5-cycle, then, , , and are pairwise-disjoint sets with cardinalities r, ,

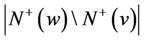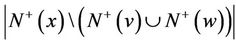, and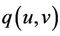, we have that

Thus, the inequality (1) holds for.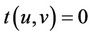

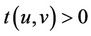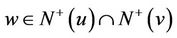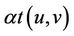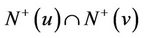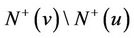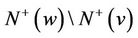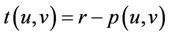We now assume. By the induction hypothesis, there is some vertex that has outdegree less than in the subdigraph of G induced by, otherwise, this subdigraph would contain a directed 5-cycle. Also, w has not more than outneighbors in the subdigraph of G induced by. Let be the outneighbors of w which is not in. Noting that, we have that

(3)

Because G has no directed triangle, all outneighbors of w are neither in 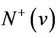nor in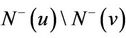. Consider the subdigraph of G induced by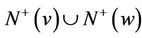, by the induction hypothesis, there is some vertex 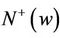that has outdegree less than 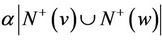in this subdigraph. Thus, the set of outneighbors of x not in satisfies

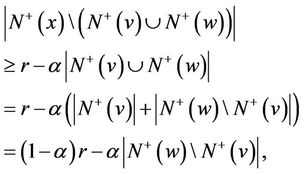(4)

Since G has no directed 4-cycle, all outneighbors of w are neither in 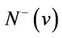nor in. Consider the subdigraph of G induced by by the induction hypothesis, there is some vertex

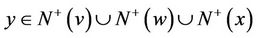
that has outdegree less than

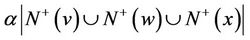
in this subdigraph. Thus, the set of outneighbors of y not in 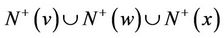satisfies

(5)

Because G has no directed cycle of length at most 5, then, ,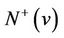

,

,

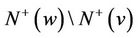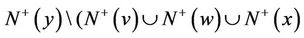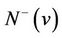and are pairwise-disjoint sets of cardinalities r, ,

,

,

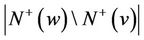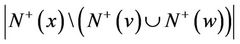and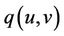, we have that

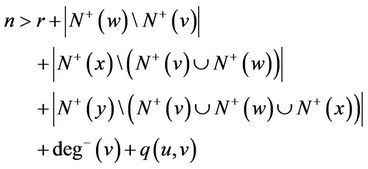
Substituting (3), (4) and (5) into this inequalities yields

as desired, and so the lemma follows.

Connect to Proof of Theorem 1.2

Recalling that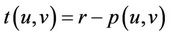, we can rewrite the inequality (1) as

(6)

Summing over all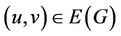, we have that

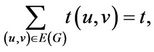(7)

where t is the number of transitive triangles in G, and

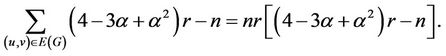(8)

By Cauchy’s inequality and the first theorem on graph theory (see, for example, Theorem 1.1 in [12]), we have that

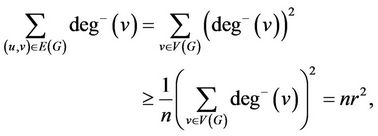
that is

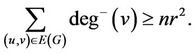(9)

Because 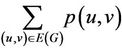and 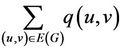are both equal to the number of induced directed 2-paths in G, it follows that

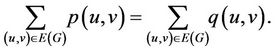(10)

Summing over all 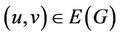for the inequality (6) and substituting inequalities (7)-(10) into that inequality yields,

(11)

Noting that 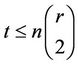(see Shen [7]), we have that

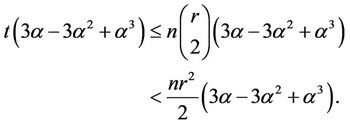(12)

Combining (11) with (12) yields

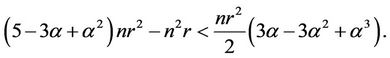(13)

Dividing both sides of the inequality (13) by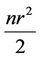and noting that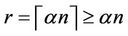, we get

that is

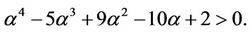
We obtain that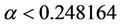, a contradiction. This completes the proof of the theorem.

REFERENCES

NOTES

^*Supported by NNSF of China (No. 11071233).

^#Corresponding author.