International Journal of Astronomy and Astrophysics
Vol.3 No.4(2013), Article ID:41086,3 pages DOI:10.4236/ijaa.2013.34060
Cosmic Engineering: Moving Asteroids
UAM, Poznan, Poland
Email: gmuse2@gmail.com
Copyright © 2013 Marcin Misiak. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 8, 2013; revised July 8, 2013; accepted July 16, 2013
Keywords: Astrodynamics; Celestial Mechanics; Orbital Motion; Optimal Control
ABSTRACT
This paper presents methods of orbit transfer for small planetoids from the main belt to the future colonies on Mars using current technologies. The results show that by using nuclear weapon or even kinetic energy weapon (for retrograde bodies) asteroids with masses up to about 100 tons can be moved. Both options assume that asteroid will survive explosion.
1. Introduction
In recent years there is a growing interest in the planetoids, concerning extraction of precious materials from them, like iron, nickel, water or platinum [1]. The common view is to send a spaceship, extract minerals and bring them back to Earth. This is an expensive, timeand effort-consuming approach. Instead we propose moving asteroids from its original place in the main belt to the planet Mars (or could be also Moon) where future human colonies will be held. The idea of modifying orbits of celestial objects was considered in literature before for example in quite fictional proposal to higher Earth orbit because of Sun’s future brightening [2].
The methods we employ are similar to those considered in the case of a deflection of an asteroid on the collision curse with the Earth [3-5].
In Chapter 2 we consider nuclear explosion in front of an asteroid, in Chapter 3 kinetic energy weapon, Chapter 4 considers the effect of light pressure on the asteroids and finally in Chapter 5 we present a short summary.
2. Nuclear Explosion
Let’s consider sending a spacecraft equipped with nuclear weapon to an asteroids. Assuming nuclear explosion just in front of an asteroid (Figure 1) huge energy will be released in high energy gamma rays and very energetic particles. This energy will slow down the asteroid.
We treat the interaction between the products of nuclear explosion and an asteroid as an inelastic collision. Supposing proportionality of momentum and energy like
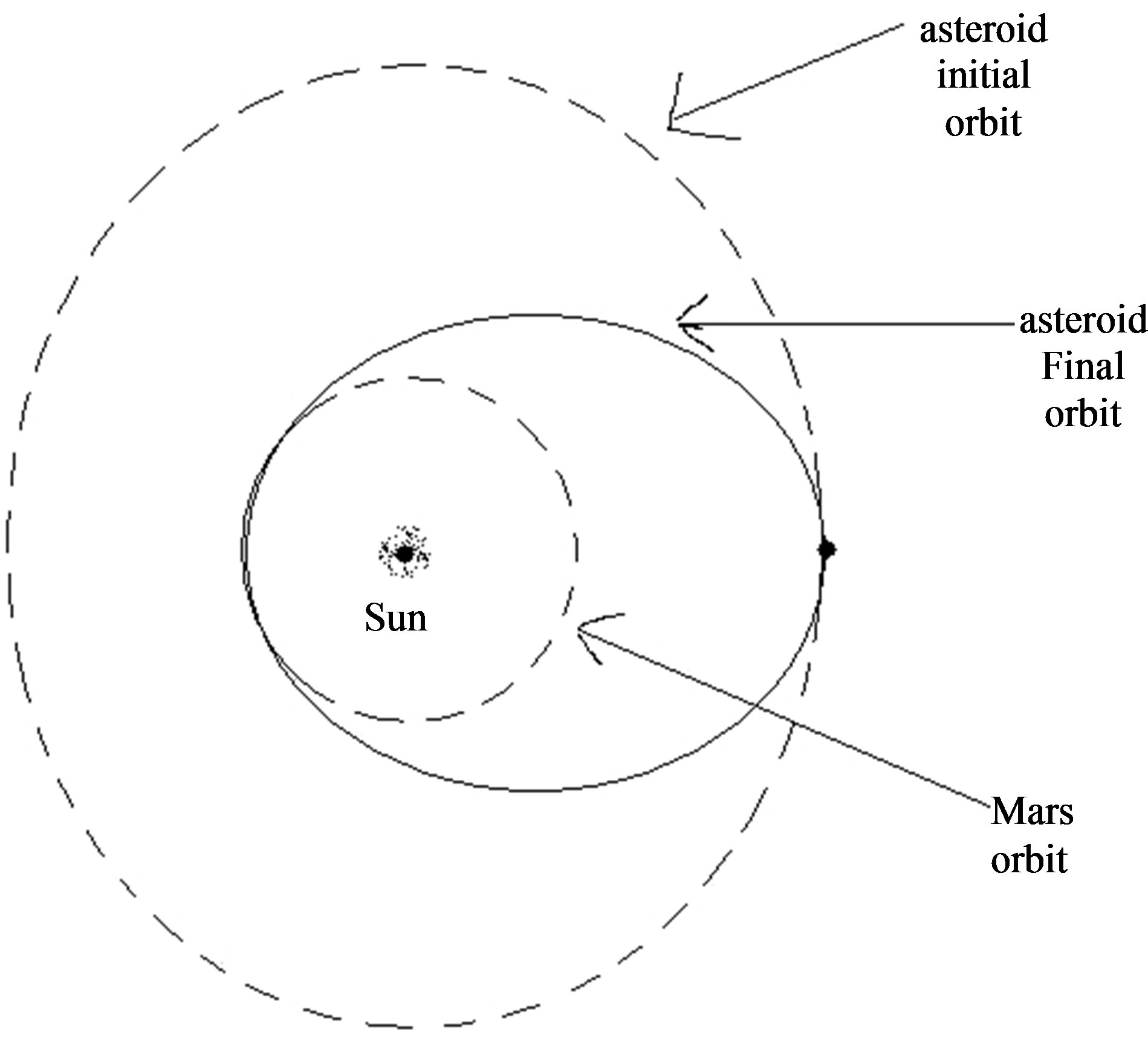
Figure 1. Trajectory of an asteroid (bold line) after nuclear explosion which took place before it.
for radiation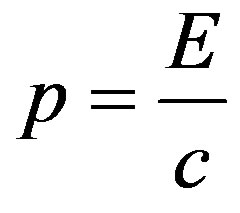 , from the conservation of momentum follows:
, from the conservation of momentum follows:
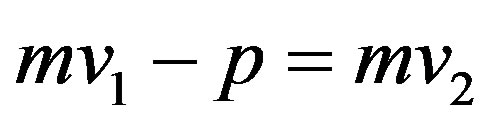
 , (1)
, (1)
where —velocity of an asteroid before explosion,
—velocity of an asteroid before explosion,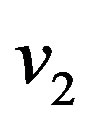 —velocity of an asteroid after the explosion,
—velocity of an asteroid after the explosion,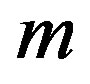 — mass of an asteroid.
— mass of an asteroid.
Hydrogen bomb can release 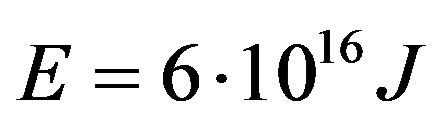 of energytypical asteroids velocity in the main belt is
of energytypical asteroids velocity in the main belt is 
and the final velocity we want to achieve is according to Hohmann transfer [6,7] between asteroid-Mars system:
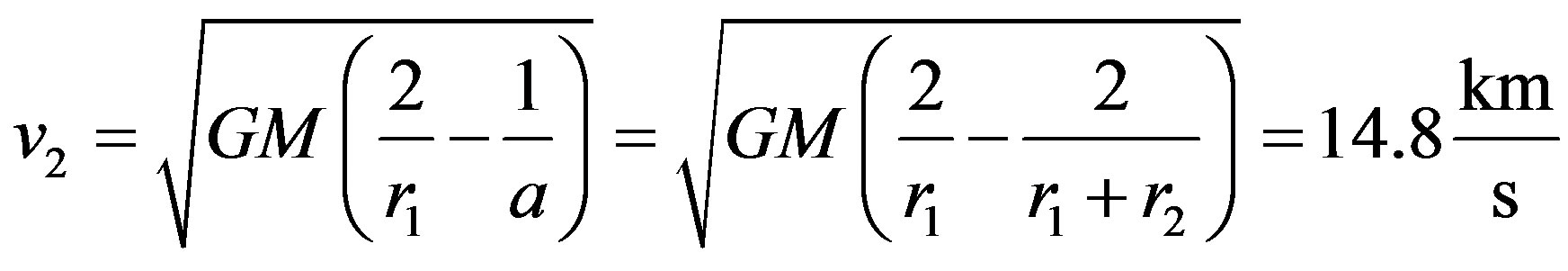
Introducing these numbers to the Equation (1) we can compute the mass of the asteroids which can be moved in this way:
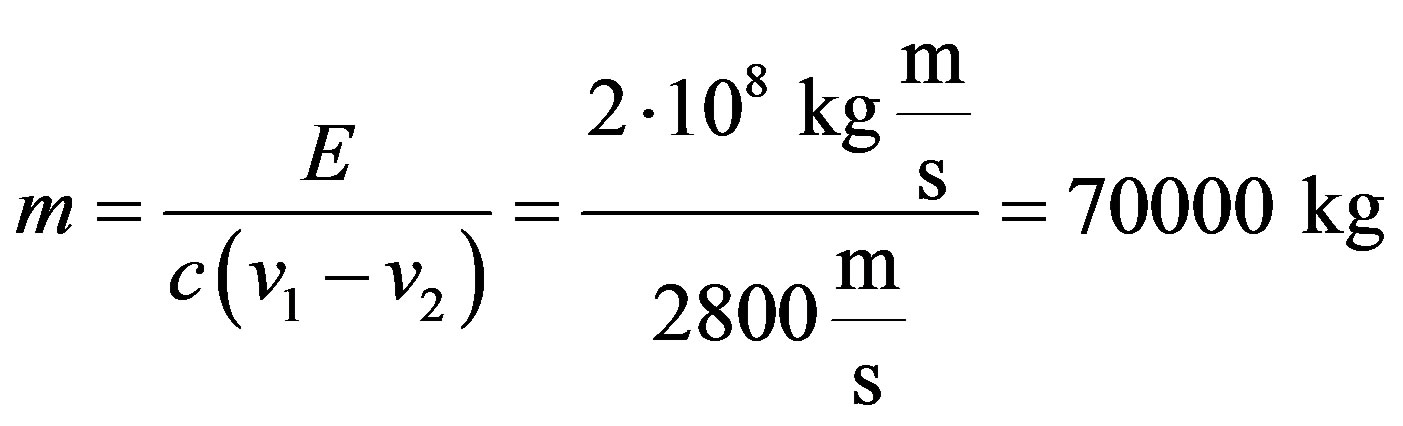
If we suppose that an asteroids is built from pure nickel, and current price 18 $/kg the asteroids will be worth more than 1 million dollars.
The similar procedure can also be applied for the Kuiper belt objects.
3. Kinetic Energy Weapon
As a second possibility to move an asteroid we consider shooting an asteroid by 5 tons weapon from the Earth orbit. This approach can be useful if we can find an asteroid which orbit the Sun in the opposite direction as the Earth does (retrograde motion) Figure 2.
In that case we can take advantage from the Earth motion around the Sun (about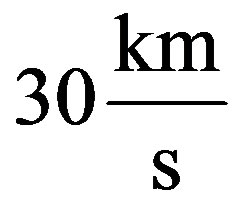 ). For an inelastic col-
). For an inelastic col-
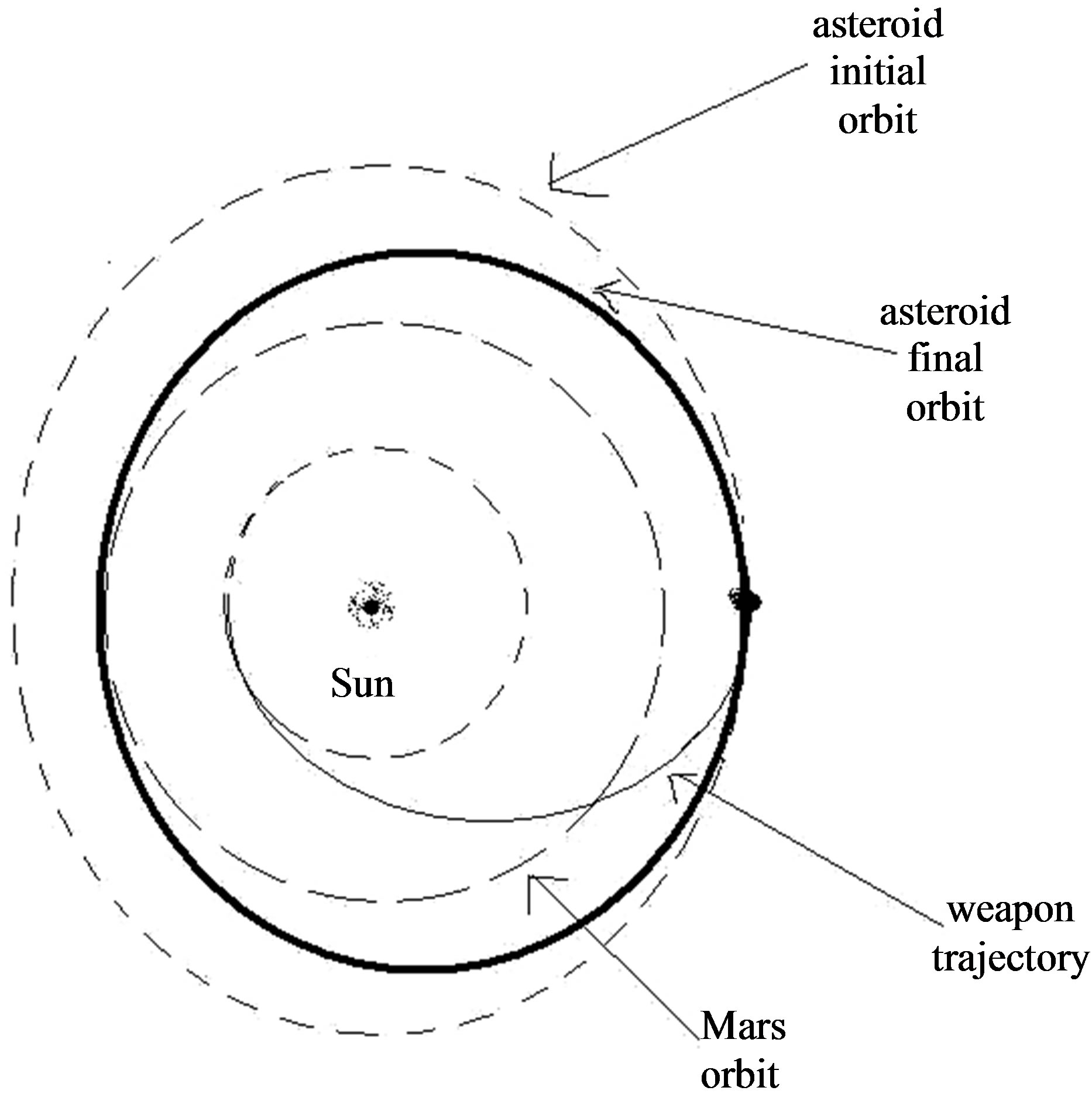
Figure 2. Trajectory of an asteroid after collision with kinetic energy weapon fired from the Earth.
lision the conservation of momentum leads to:
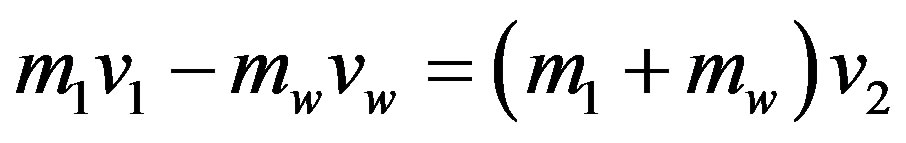
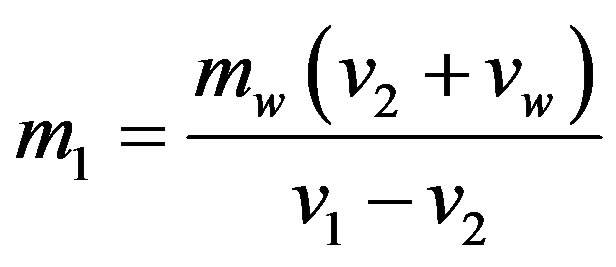 , (2)
, (2)
where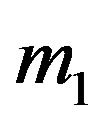 —mass of an asteroid, where
—mass of an asteroid, where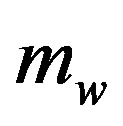 —mass of a weapon,
—mass of a weapon,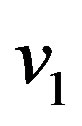 —velocity of an asteroid before the collision,
—velocity of an asteroid before the collision, —velocity of an asteroid after the collision,
—velocity of an asteroid after the collision,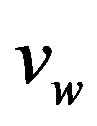 —velocity of the weapon.
—velocity of the weapon.
The velocity of the weapon shot from the Earth in the moment of collision is:
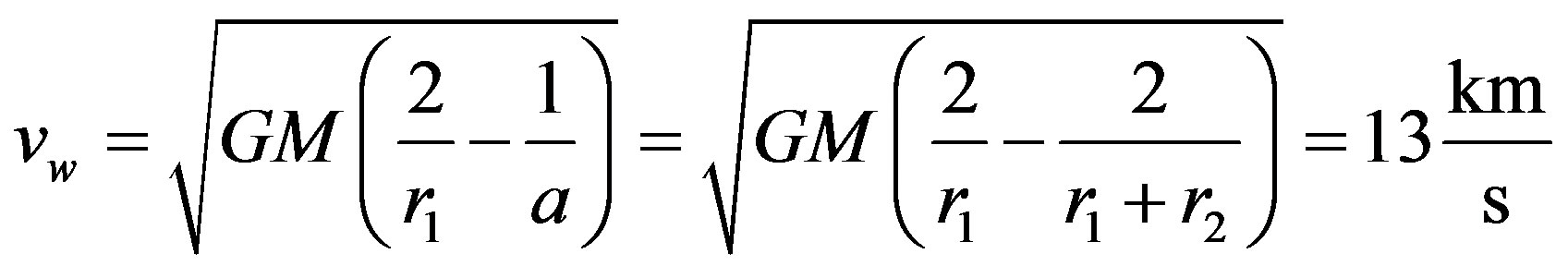
Substituting this and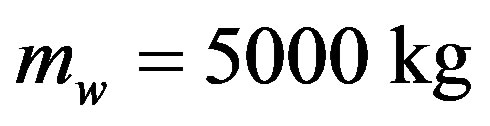 ,
, 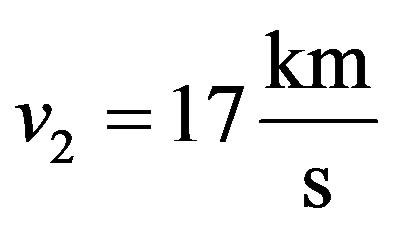 to the Equation (2) we get:
to the Equation (2) we get:
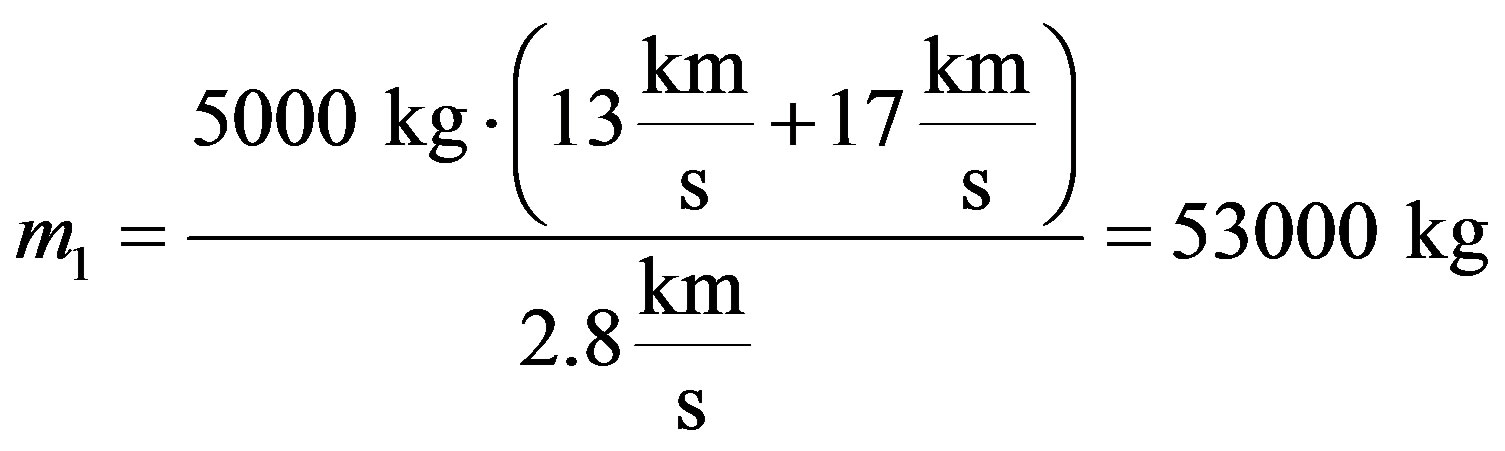
We can also consider an elastic collision, which is probably more difficult to construct (something like air bags used by NASA in Mars missions). In this case from the conservation of momentum and energy follows:
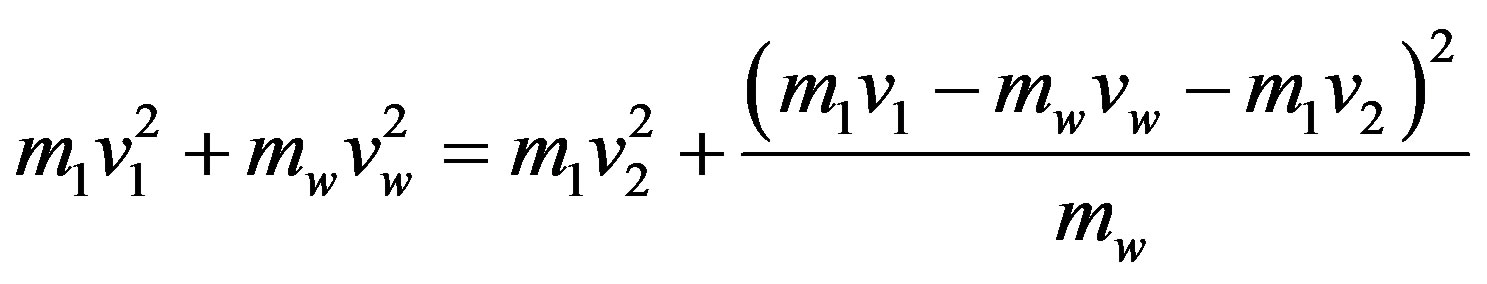
which after substitution yields to:
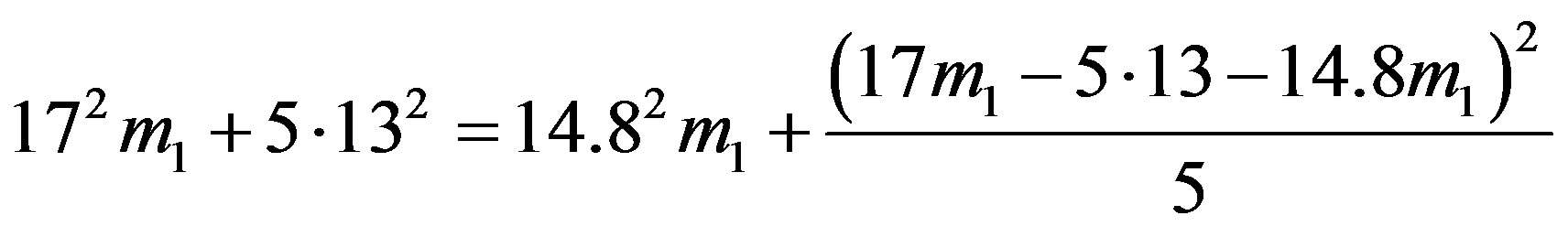
The solution of the above equation gives for the mass of the asteroids possible to transfer in this way:
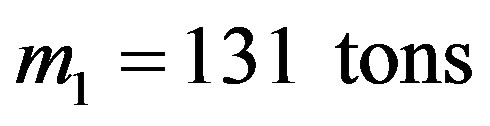
This value is more than twice the mass possible to move through inelastic collision.
4. Solar Sail
As a third possibility for moving asteroid to a desired position let’s consider attaching a huge solar sail. The average force in Newton’s acting on a sail from light pressure at a distance about 2AU is:
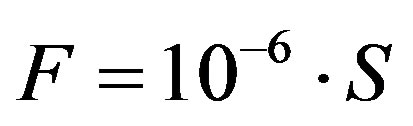 where
where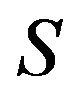 —area of the sail in square meter.
—area of the sail in square meter.
Considering sail with area 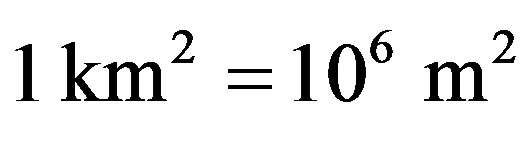 we get the force about
we get the force about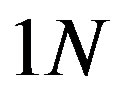 . Depending on the orientation of the sail we can move asteroid spiralling inward or outward from the Sun [8]. In the case of moving asteroid from the main belt to Mars we need inward spiralling and orientation of the sail shown in Figure 3. In this case the force has two components: radial
. Depending on the orientation of the sail we can move asteroid spiralling inward or outward from the Sun [8]. In the case of moving asteroid from the main belt to Mars we need inward spiralling and orientation of the sail shown in Figure 3. In this case the force has two components: radial  and tangential
and tangential  , where
, where 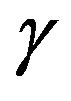 is the angle between sun light and the line perpendicular to the sail.
is the angle between sun light and the line perpendicular to the sail.
Substituting  the mass of the asteroids possible to move in about a year is:
the mass of the asteroids possible to move in about a year is:
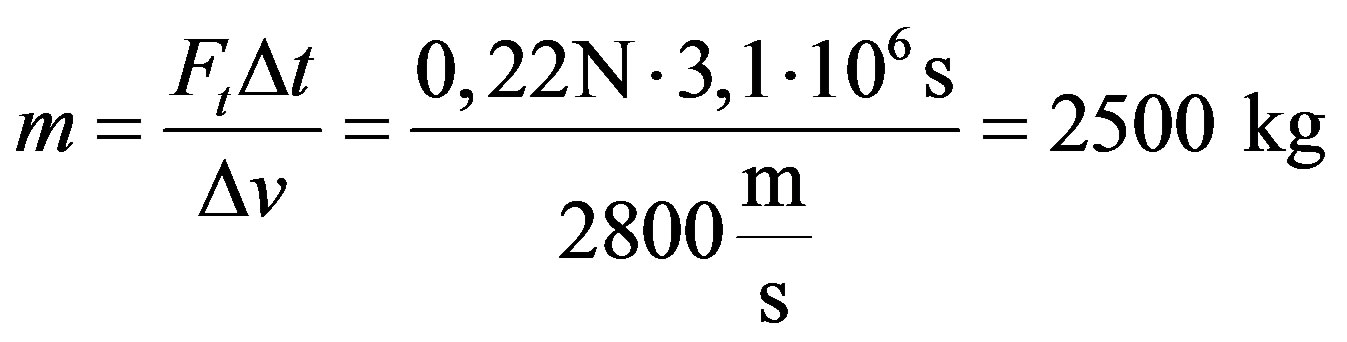
Another option using the pressure of the light which can be considered is to attach small nuclear reactor equipped with a laser to an asteroid. In this scenario the energy generated by nuclear reactions is used to power the laser. The beam of light from the laser is sent in the direction of the velocity of the asteroid. As a result asteroid will spiral from the main belt inward the Sun and can reach the Mars orbit. If the reactor has the mass M and the power 100 MW the mass of the asteroid which can be transferred from the main belt to the Mars in a year is about:
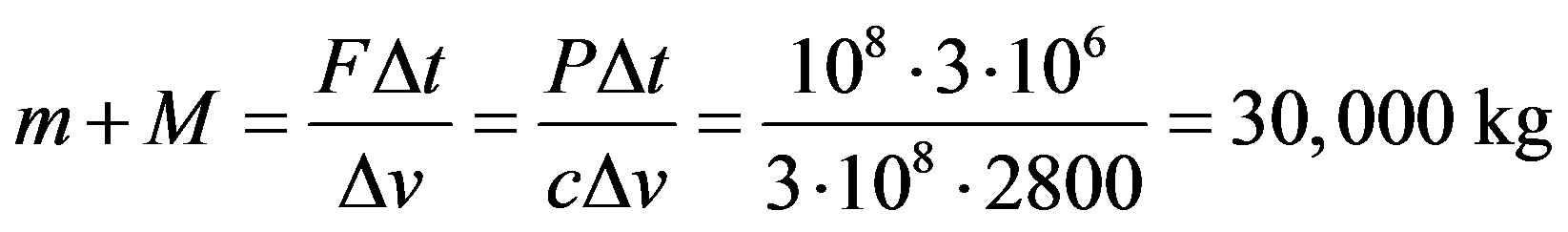

Figure 3. Attaching properly solar sail to asteroid can move it towards the Sun.
Assuming mass of the reactor with fuel , mass of the asteroid is also
, mass of the asteroid is also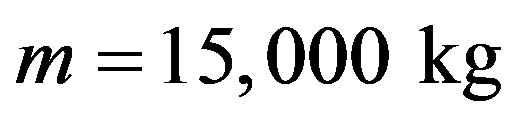 .
.
5. Summary
From the options considered, the most universal is a nuclear blast in front of the asteroid. The biggest possible mass to move from the main belt to Mars we got in elastic collision between missiles ejected from the Earth and an asteroid is 131,000 kg. However this possibility requires finding an asteroid which orbits the Sun in the opposite direction. Both options assume that asteroid will survive explosion (collision). The last options, solar sail for main belt asteroids and nuclear reactor + laser for any asteroid are not destructive and most safe; however allow only moderate masses to transfer.
REFERENCES
- http://en.wikipedia.org/wiki/Asteroid_mining, http://www.planetaryresources.com/, http://deepspaceindustries.com/
- D. G. Korycansky, G. Laughlin and F. C. Adams, “Astronomical Engineering: A Strategy for Modifying Planetary Orbits,” Astrophysics and Space Science, Vol. 275, No. 4, 2001, pp. 349-366. http://dx.doi.org/10.1023/A:1002790227314
- L. A. Kleiman, “Project Icarus,” MIT Press, Cambridge, 1968.
- J. Gil-Fernández, R. Panzeca and C. Corral, “Impacting Small Near Earth Objects,” Advances in Space Research, Vol. 42, No. 8, 2008, pp. 1352-1363. http://dx.doi.org/10.1016/j.asr.2008.02.023
- T. Lu and S. G. Love, “Gravitational Tractor for Towing Asteroids,” Nature, Vol. 438, 2005, pp. 177-178.
- A. E. Roy, “Orbital Motion,” IOP Publishing Ltd, Bristol, 2005.
- R. R. Bate, D. D. Mueller and J. E. White, “Fundamentals of Astrodynamics,” Courier Dover Publications, Mineola, 1971.
- M. Subotowicz, “Elementy Astronautyki,” Wydawnictwa Szkolne i Pedagogiczne (WSiP), Warszawa, 1974. (in Polish)

