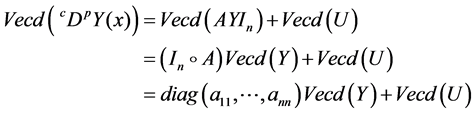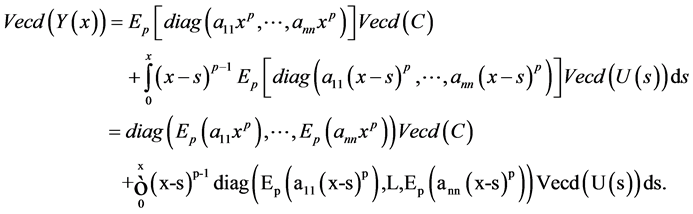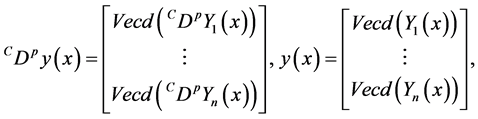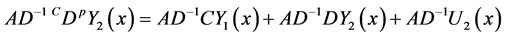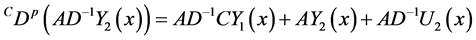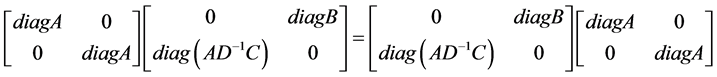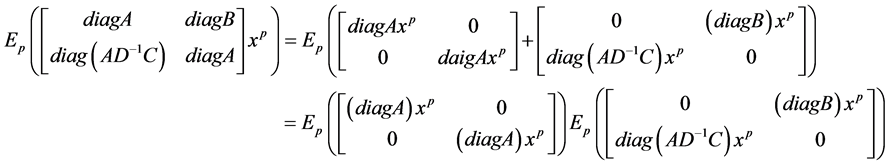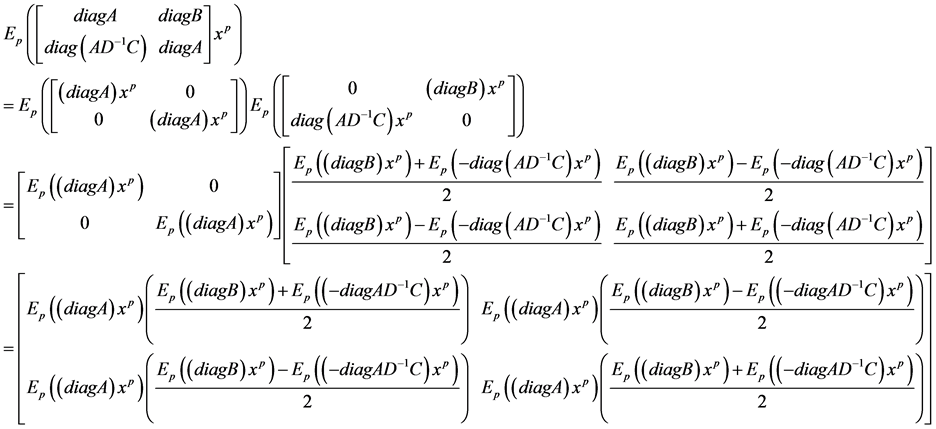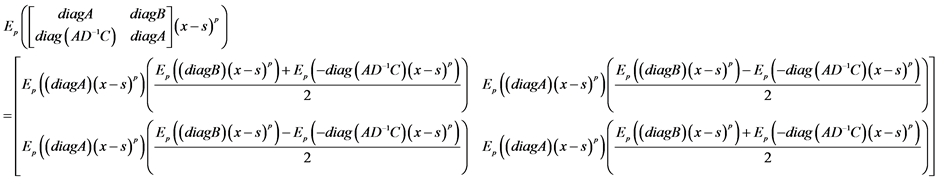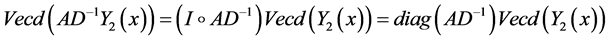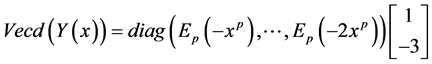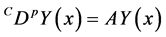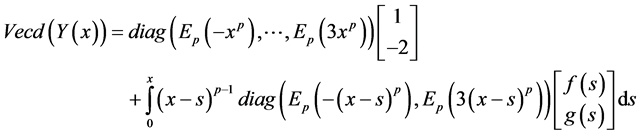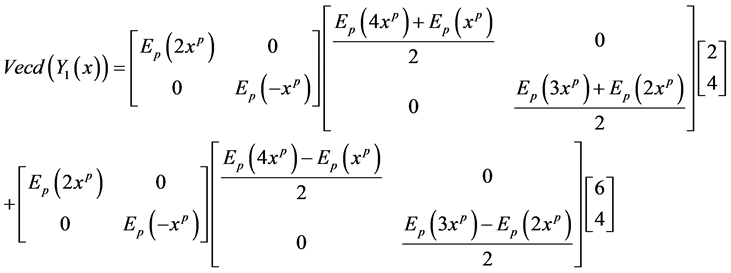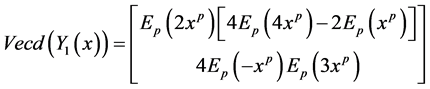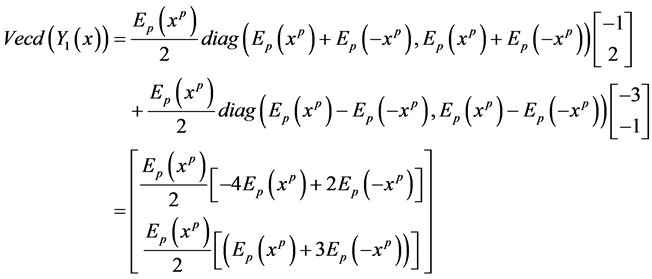Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63982,11 pages
10.4236/jamp.2016.42049
The Exact Solutions of Such Coupled Linear Matrix Fractional Differential Equations of Diagonal Unknown Matrices by Using Hadamard Product
Zayed Al-Zuhiri1, Zeyad Al-Zhour2, Khaled Jaber1
1Department of Mathematics, Faculty of Science and Information Technology, Zarqa University, Zarqa, Jordan
2Department of Basic Sciences and Humanities, College of Engineering, University of Dammam, Dammam, Saudi Arabia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 September 2015; accepted 26 February 2016; published 29 February 2016
ABSTRACT
In this paper, we present the general exact solutions of such coupled system of matrix fractional differential equations for diagonal unknown matrices in Caputo sense by using vector extraction operators and Hadamard product. Some illustrated examples are also given to show our new approach.
Keywords:
Fractional Operators, Matrix Fractional Differential Equations, Hadamard Product, Vector Extraction Operator

1. Introduction
Fractional calculus attracted the attention of researchers because of its application in physics as the nonlinear oscillation of earthquake can be modeled with fractional derivatives [1] , and the fluid-dynamic traffic model with fractional derivatives [2] can eliminate the deficiency arising from the assumption of continuum traffic flow. Based on experimental data fractional, partial differential equations for seepage flow in porous media are suggested in [3] , and differential equations with fractional order have recently proved to be valuable tools to the modeling of many physical phenomena [4] . A review of some applications of fractional derivatives in continuum and statistical mechanics is given by Mainardi [5] . The analytic results on the existence and uniqueness of solutions of the fractional differential equations have been investigated by many authors see as an example [6] . During the last decades, several methods have been used to solve fractional differential equations, fractional partial differential equations, fractional integro-differential equations and dynamic systems containing fractional derivatives, such as Adomian’s decomposition method [7] , variational iteration method [8] - [11] , homotopy perturbation method [12] , homotopy analysis method [13] , spectral methods [14] , and other methods [15] .
Recently, Wang [16] studied the synchronized motions in a star network of coupled fractional order systems in which the major element is coupled to each of the non-interacting individual elements and Kilicman and Al- Zhour [17] studied several operational matrices for fractional integration and differentiation and expanded the Kronecker convolution product to the Riemann-Liouville fractional integral of matrices. Al-Zhour [18] introduced the exact solution of coupled fractional order systems by using Kronecker structure.
In the present paper, the exact solutions of coupled and uncoupled systems of matrix fractional differential equations for diagonal unknown matrices are presented by using a new attractive method and some illustrated examples are also given to show our new approach.
2. Basic Results and Preliminaries
In this section, we recall some basic results and definitions associated to Hadamard product, Mittage-Leffler function and Caputo fractional derivative that will be used to get our results later.
Definition 2.1. Let 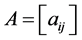 and
and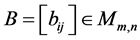 .Then the Hadamard product of A and B is defined by [19] - [26] .
.Then the Hadamard product of A and B is defined by [19] - [26] .
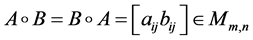 (2-1)
(2-1)
Definition 2.2. Let 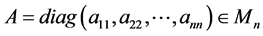 be a diagonal matrix. Then the diagonal extraction operator of A is defined by [21] [23] .
be a diagonal matrix. Then the diagonal extraction operator of A is defined by [21] [23] .
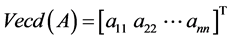 (2-2)
(2-2)
Theorem 2.3. Let 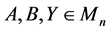 be diagonal matrices. Then
be diagonal matrices. Then
 (2-3)
(2-3)
Definition 2.4. The one parameter Mittage-Leffler functions and Mittage-Leffler matrix functions of matrix 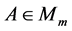 are defined, respectively, for
are defined, respectively, for 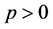 by [18] .
by [18] .
 (2-4)
(2-4)
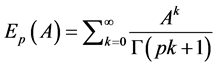 . (2-5)
. (2-5)
Note that the Mittage-Leffler matrix function of  can be represented by using spectral decomposition method by [18] .
can be represented by using spectral decomposition method by [18] .
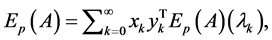 (2-6)
(2-6)
where 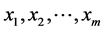 and
and 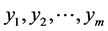 are the eigenvectors corresponding to the eigenvalue
are the eigenvectors corresponding to the eigenvalue 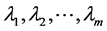
Theorem 2.5. Let 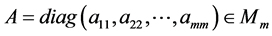
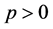
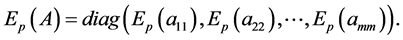
Definition 2.6. The Caputo fractional derivative of 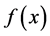
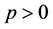


Theorem 2.7. The relationship between the Mittage-Leffler function and Caputo derivative are given by:
a)
b)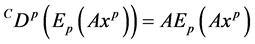
3. Main Results
In this section, we present the general exact solutions of the coupled and uncoupled system of fractional differential equations for diagonal unknown matrices by using the using vector extraction operators and Hadamard product.
Lemma 3.1. Let 
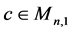
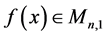
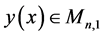

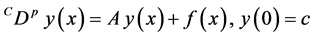
is given by:
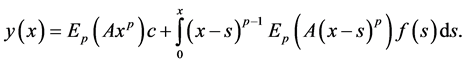
Theorem 3.2. Let 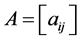
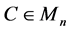
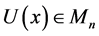
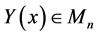

is given by:

Proof. By using (2-3), then (3.3) can be represented by:
Hence, the vector extraction solution of (3.3) is given by:
Theorem 3.3. Let 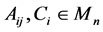
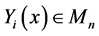

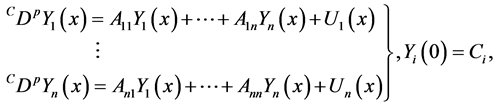
is given by:
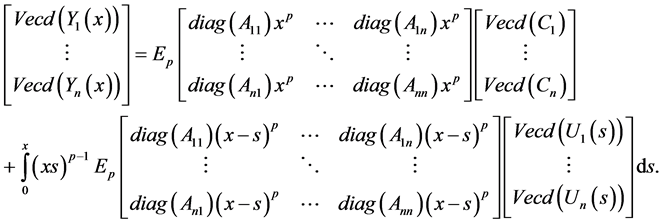
Proof. By using (2-3), then (3.5) can be represented by:

Now by letting
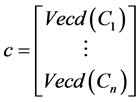

Hence by using Lemma 3.1 and simple computations, then we get the solution as in (3-6).
Below we will discuss some important special cases of the general system as in Theorem 3.3.
Theorem 3.4. Let 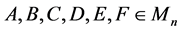
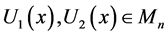
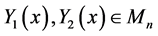
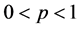
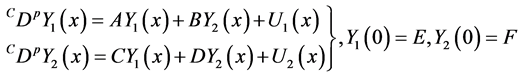
are given by:
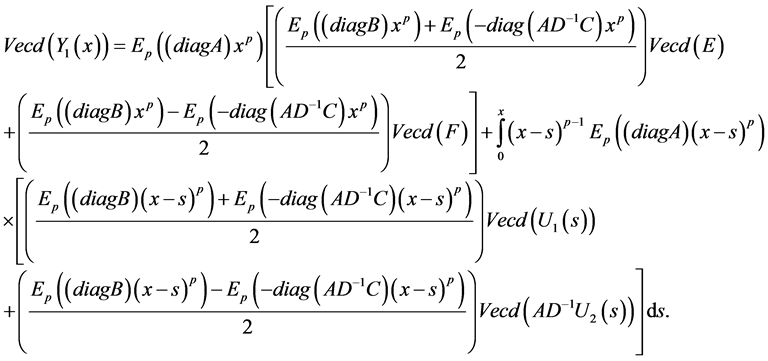
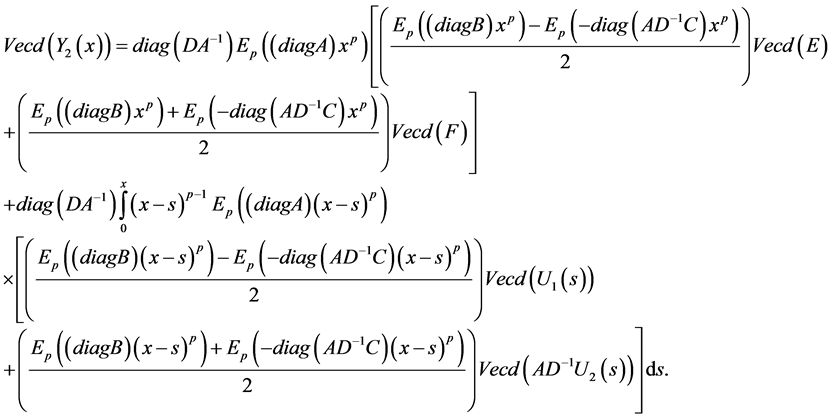
Proof. By multiplying the second equation in (3-9) by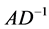
Then (3-9) can be written as
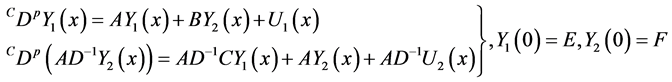
Now, by using 

Now by using (3-6), then the solution of (3.13) is given by:
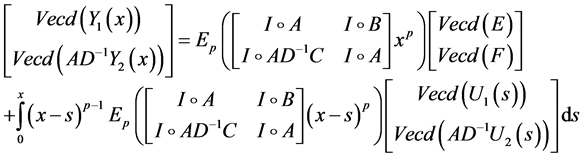
Now we deal with
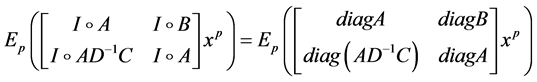
Since
Then
But

and
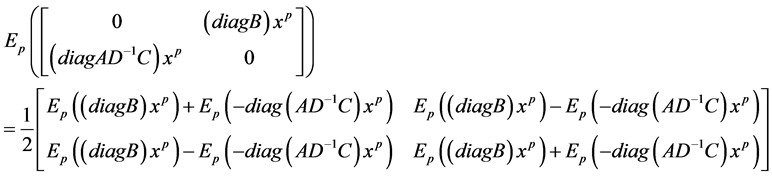
So,
(3.18)
Similarly,
(3.19)
Now from (3-13), (3-18) and (3-19), we get
Since,
Then, we get the vector extraction solution as in (3-11).
Corollary 3.5. Let 
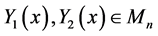
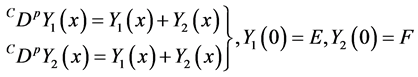
are given by:
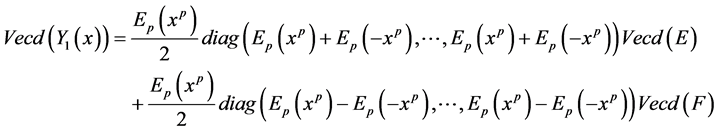

Proof. The proof is straightforward by applying Theorem 3.4 by letting 

4. Illustrated Examples
In the section, we give some illustrated examples to show our new approach as discussed in above section.
Example 4.1. Consider the following matrix linear fractional differential equation:
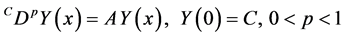
where 
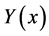
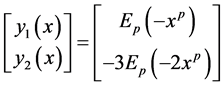
Example 4.2. Consider the following system of order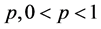
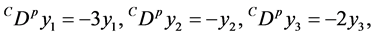
where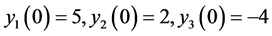

Now the exact solution of (4-3) by applying Theorem 3.2 is given by:
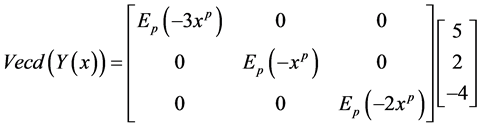
Example 4.3. Consider the following matrix fractional differential equation:
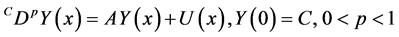
where 

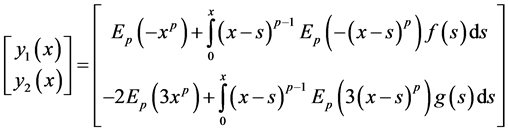
Example 4.4. Consider the following matrix fractional differential equations of order
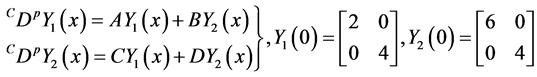
where 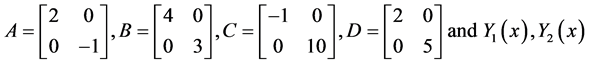
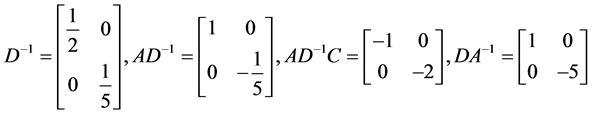
Then the exact solution of (4-5) by applying Corollary 3.5 is given by:
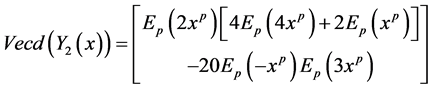
Example 4.5. Consider the following coupled matrix fractional differential equations:
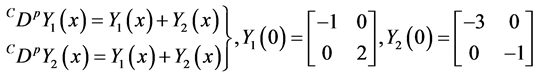
Then the exact solution by applying Corollary 3.5 is given by:
5. Conclusion
The general exact solutions of coupled system of matrix fractional differential equations with diagonal matrices coefficients by using vector extraction operators and Hadamard product in Caputo sense are presented with some illustrated examples. How to find the complexity of this method requires further research.
Acknowledgements
The authors express their sincere thanks to referees for very careful reading and helpful suggestion of this paper.
Cite this paper
ZayedAl-Zuhiri,ZeyadAl-Zhour,KhaledJaber, (2016) The Exact Solutions of Such Coupled Linear Matrix Fractional Differential Equations of Diagonal Unknown Matrices by Using Hadamard Product. Journal of Applied Mathematics and Physics,04,432-442. doi: 10.4236/jamp.2016.42049
References
- 1. He, J. (1998) Nonlinear Oscillation with Fractional Derivative and Its Applications. International Conference on Vibrating Engineering, Dalian, 288-291.
- 2. He, J. (1999) Some Applications of Nonlinear Differential Equations and Their Approximations. Bulletin of Science and Technology, 15, 86-90.
- 3. He, J. (1998) Approximate Analytical Solution for Seepage Flow with Fractional Derivatives in Porous Media. Computer Methods in Applied Mechanics and Engineering, 167, 57-68.
http://dx.doi.org/10.1016/S0045-7825(98)00108-X - 4. Grigorenko, I. and Grigorenko, E. (2003) Chaotic Dynamics of the Fractional Lorenz System. Physical Review Letters, 91, 34-101.
http://dx.doi.org/10.1103/PhysRevLett.91.034101 - 5. Mainardi, F. (1997) Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics, Fractals and Fractional Calculus in Continuum Mechanics. Springer-Verlag, New York, 291-348.
http://dx.doi.org/10.1007/978-3-7091-2664-6_7 - 6. Kilbas, A., Srivastava, H. and Trujillo, J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier, San Diego.
- 7. Momani, S. and Shawagfeh, N. (2006) Decomposition Method for Solving Fractional Riccati Differential Equations, Applied Mathematics and Computation, 182, 1083-1092.
http://dx.doi.org/10.1016/j.amc.2006.05.008 - 8. Momani, S. and Odibat, Z. (2006) Analytical Approach to Linear Fractional Partial Differential Equations Arising in Fluid Mechanics. Physics Letters A, 355, 271-279.
http://dx.doi.org/10.1016/j.physleta.2006.02.048 - 9. Momani, S. and Odibat, Z. (2007) Homotopy Perturbation Method for Nonlinear Partial Differential Equations of Fractional Order. Physics Letters A, 365, 345-350.
http://dx.doi.org/10.1016/j.physleta.2007.01.046 - 10. Odibat, Z. and Momani, S. (2008) Modified Homotopy Perturbation Method: Application to Quadratic Riccati Differential Equation of Fractional Order. Chaos, Solitons and Fractals, 36, 167-174.
http://dx.doi.org/10.1016/j.chaos.2006.06.041 - 11. Odibat, Z. and Momani S. (2006) Application of Variational Iteration Method to Nonlinear Differential Equations of Fractional Order. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 271-279.
http://dx.doi.org/10.1515/IJNSNS.2006.7.1.27 - 12. Hashim, I., Abdulaziz, O. and Momani, S. (2009) Homotopy Analysis Method for Fractional IVPs. Communications in Nonlinear Science and Numerical Simulation, 14, 674-684.
http://dx.doi.org/10.1016/j.cnsns.2007.09.014 - 13. Rawashdeh, E.A. (2006) Numerical Solution of Fractional Integro-Differential Equations by Collocation Method. Applied Mathematics and Computation, 176, 1-6.
http://dx.doi.org/10.1016/j.amc.2005.09.059 - 14. Mathai, A. and Haubold, H. (2008) Special Functions for Applied Scientists. Springer Science and Business Media Ltd., New York.
http://dx.doi.org/10.1007/978-0-387-75894-7 - 15. Wang, J. and Zhang, Y. (2010) Network Synchronization in a Population of Star-Coupled Fractional Nonlinear Oscillators. Physics Letter A, 374, 1464-1468.
- 16. Wang, Q. (2006) Numerical Solutions for Fractional KdV-Burgers Equation by Adomian Decomposition Method. Applied Mathematics and Computation, 182, 1048-1055.
http://dx.doi.org/10.1016/j.amc.2006.05.004 - 17. Kilicman, A. and Al-Zhour, Z. (2007) Kronecker Operational Matrices for Fractional Calculus and Some Applications. Applied Mathematics and Computation, 187, 250-265.
http://dx.doi.org/10.1016/j.amc.2006.08.122 - 18. Al-Zhour, Z. (2014) The General (Vetor) Solutions of Such Linear (Coupled) Matrix Fractional Differential Equations by Using Kronecker Structures. Applied Mathematics and Computation, 232, 498-510.
http://dx.doi.org/10.1016/j.amc.2014.01.079 - 19. Balachandran, K., Kokila, J. and Trujillo, J. (2012) Relative Controllability of Fractional Dynamicsystems with Multiple Delays in Control. Applied Mathematics and Computation, 64, 3037-3045.
http://dx.doi.org/10.1016/j.camwa.2012.01.071 - 20. Balachandran, K. and Kokila, J. (2012) On the Controllability of Fractional Dynamic Systems. International Journal of Applied Mathematics and Computer Science, 22, 523-531.
- 21. Al-Zhour, Z. (2012) Efficient Solutions of Coupled Matrix and Matrix Differential Equations. Intelligent Control and Automation, 3, 176-187.
http://dx.doi.org/10.4236/ica.2012.32020 - 22. Kiliçman, A. and Al-Zhour, Z. (2009) On the Connection between Kronecker and Hadamard Convolution Products of Matrices and Some Applications. Journal of Inequalities and Applications, 2009, Article ID: 736243.
- 23. Al-Zhour, Z. (2008) A Computationally-Efficient Solutions of Coupled Matrix Differential Equations for Diagonal Unknown Matrices. Journal of Mathematical Sciences: Advances and Applications, 1, 373-387.
- 24. Kiliçman, A. and Al-Zhour, Z. (2007) Vector Least-Squares Solutions of Coupled Singular Matrix Equations. Journal of Computational and Applied Mathematics, 206, 1051-1069.
http://dx.doi.org/10.1016/j.cam.2006.09.009 - 25. Al-Zhour, Z. and Kiliçman, A. (2007) Some New Connections between Matrix Products for Partitioned and Non-Partitioned Matrices. Computers & Mathematics with Applications, 54, 763-784.
http://dx.doi.org/10.1016/j.camwa.2006.12.045 - 26. Al-Zhour, Z. and Kiliçman, A. (2006) Matrix Equalities and Inequalities Involving Khatri-Rao and Tracy-Singh Sums. Journal of Inequalities in Pure and Applied Mathematics, 7, 496-513.