ABSTRACT

Based on the -expansion method, a series of exact solutions of the generalized Benjamin equation have been obtained. The travelling wave solutions are expressed by the hyperbolic functions, the trigonometric functions and the rational functions. It is shown that the 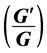-expansion method is concise, and its applications are promising.

Keywords

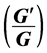-Expansion Method, Generalized Benjamin Equation, Nonlinear Evolution Equations

1. Introduction

It is well known that seeking exact solutions for nonlinear evolution equations (NLEES) plays an important role in mathematical physics. In the past five decades or so, many effective methods have been presented, which contain the inverse scattering method [1] , Hirota bilinear method [2] , the tanh-function method and its various extension [3] [4] , the sine-cosine function method [5] [6] , homogeneous balance method [7] [8] , Jacobi elliptic function method [9] [10] , the first-integral method [11] [12] , the sine-Gordon equation method [13] and the Exp-function method [14] -[16] .

Recently, Wang et al. [17] proposed a new method called the 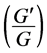-expansion method to look for travelling wave solutions of nonlinear evolution equations (NLEEs). The 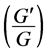-expansion method is based on the assumptions that the travelling wave solutions can be expressed by a polynomial in 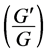as follows:

(1)

where 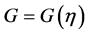satisfies a second order linear ordinary differential equation (LODE):

(2)

where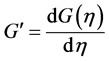, , 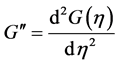, 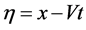and 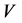is a constant. The degree of the polynomial can be determined by considering the homogeneous balance between the highest order derivative and nonlinear terms appearing in the given NLEE. The coefficients of the polynomial can be obtained by solving a set of algebraic equations resulted from the process of using the method. By using the 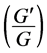-expansion method, many nonlinear equations [17] -[27] have been successfully solved.

In the present paper, we will extend the -expansion method to the following generalized Benjamin equation:

(3)

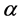where and 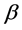are constants. Equation (3) is used in the analysis of long wave in shallow water; see [28] . To the best of our knowledge, there are a few articles about this equation. Recently, by applying the extended tanh method, Taghizadeh et al. [29] obtained some exact solutions. In the subsequent section, we will illustrate the -expansion method in detail with the generalized Benjamin equation.

2. Exact Solutions to the Generalized Benjamin Equation

First, in this section, we start out our study for Equation (3). Firstly, making the following wave variable

(4)

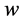where, and are constants to be determined later, Equation (3) becomes the ODE

(5)

where the prime denotes the derivation with respect to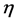. Integrating Equation (5), twice and setting the constant of integrating to zero, we obtain

(6)

Then, making the following transformation

(7)

We can obtain an equation for 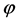as

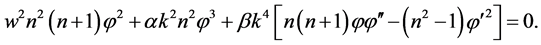(8)

Now, we make an ansatz (1) for the solution of Equation (8). Balancing the terms and in Equation (8) yields the leading order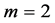. Therefore, we can write the solution of Equation (8) in the form

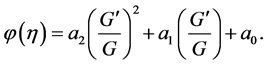(9)

Substituting (2) and (9) into (8), collecting the coefficients of 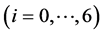and set it to zero we obtain the following system of algebraic equations for:, , , , 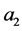, 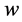and:

Solving the above system by Matlab gives

(10)

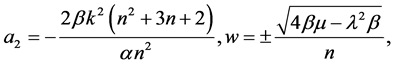(11)

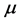where, , and are arbitrary constants.

Substituting (10) (11) into (9) yields:

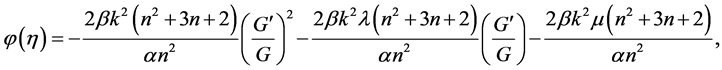(12)

where.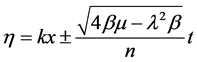

Substituting the general solutions of Equation (2) into the formulae (12) we have three types of travelling wave solutions of the generalized Benjamin equation as follows:

When,

(13)

where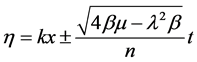, , 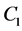and are arbitrary constants. It is easy to see that the hyperbolic solution (13) can be rewritten at, as follows

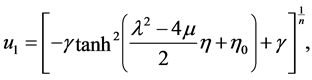(14)

while at, one can obtain

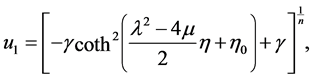(15)

where.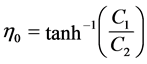

When,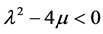

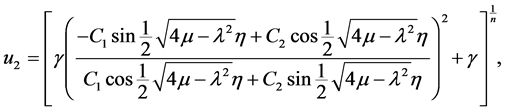(16)

where, , 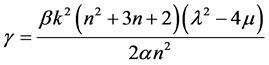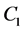and are arbitrary constants. Similarity, it is easy to see that the trigonometric solution (16) can be rewritten at 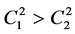and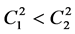, as follows

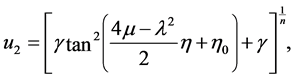(17)

and

(18)

where.

When,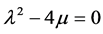

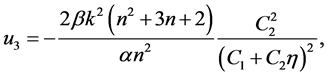(19)

where, 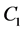and are arbitrary constants.

Authors [29] have looked for exact solutions of Equation (3) using the wave variable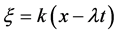, Equation (3) should become the ODE

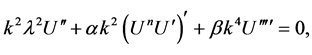(20)

not the ODE (7) in [29] in the following form

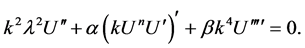(21)

Therefore, the exact solutions given in [29] are wrong. To the best of our knowledge, solutions (13), (16) and (19) have not been reported in literature.

3. Conclusion

The 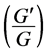-expansion method has been successfully applied here to seek exact solutions of the generalized Benjamin equation. As a result, a series of new exact solutions are obtained. The solution procedure is very simple and the travelling wave solutions are expressed by the hyperbolic functions, the trigonometric functions and the rational functions. To the best of our knowledge, these solutions have not been reported in literature. It is shown that the 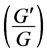-expansion method provides a very effective and powerful mathematical tool for solving nonlinear equations in mathematical physics.

Acknowledgements

This work was supported by the research project of Yuncheng University (No.YQ-2011013, YQ-2011068, XK- 2012004).

References