Theoretical Economics Letters
Vol.08 No.14(2018), Article ID:88060,18 pages
10.4236/tel.2018.814197
Post-Earnings-Announcement Drift Anomaly in India: A Test of Market Efficiency
Harshita1, Shveta Singh2, Surendra S. Yadav2
1FORE School of Management, New Delhi, India
2Indian Institute of Technology Delhi, New Delhi, India
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 17, 2018; Accepted: October 23, 2018; Published: October 26, 2018
ABSTRACT
Anomalies are deviations from Efficient Market Hypothesis (EMH), one of the primary areas of research in the field of financial economics. The paper aims to examine the presence of one such deviation―the post-earnings-announcement-drift (PEAD) anomaly―in the Indian stock market over the period 2002 to 2017. Examining the PEAD anomaly appears to be an under-researched area for India, one of the fastest growing major economies of the world. Cross-sectional Fama and MacBeth [1] regression and paired t-test are the tools employed for the analysis. The results exhibit statistically significant PEAD and the findings are robust to sub-period analysis. The anomaly persists even after accounting for other variables―beta, market capitalization, price-to-book ratio (P/B ratio), illiquidity and idiosyncratic volatility. While regulators can employ the findings as input to meet their aim of achieving market efficiency, traders and investors can design their strategies to exploit the anomalous behavior.
Keywords:
Standardized Unexpected Earnings (SUE), Post-Earnings-Announcement-Drift (PEAD), Earnings Momentum, Indian Stock Market, Market Efficiency, Market Anomalies

1. Introduction
Efficient market hypothesis (EMH) is argued to be “one of the most hotly contested propositions in all the social sciences” [2] . It is defined as “the notion that stocks already reflect all available information” [3] . Depending upon the scope of “information”, efficiency has three forms. The focus of this study is the semi-strong form of market efficiency, wherein “information” envelops all the publicly available data. According to Bodie et al. [3] , “The semi-strong-form hypothesis states that all publicly available information regarding the prospects of a firm must be reflected already in the stock price”. Thus, if a market is semi-strong form efficient, the stock prices fully reflect all the publicly available data. As earnings announcement is a publicly available information, the semi-strong form of market efficiency implies that its content should be immediately incorporated in stock prices [4] . Any delay in its incorporation or the ability to predict the direction of stock price movement based on this information is, therefore, an evidence against semi-strong form of efficiency. The post-earnings-announcement-drift (PEAD), therefore, qualifies as an anomaly because its presence signifies market inefficiency. The tendency of stock prices to drift (over time) in the direction of earnings surprise post the announcement of earnings is termed as PEAD anomaly. If the element of surprise in the announced earnings is positive in magnitude, the stock prices drift positively and vice versa. This, in turn, implies that based on the magnitude of earnings surprise, the direction of price drift can be predicted.
While genesis of the anomaly dates back to roughly half a century (it was first reported by Ball and Brown [5] ), its investigation for the Indian stock market remains an under-researched area. As Truong [6] puts it, “Strong growth in the Asia-Pacific economies and financial markets has created a rising tide of research focusing on this region. Despite this surge, investigations of PEAD for this region still remains relatively dormant”. Indian stock market is one of the favorite destinations in the Asia-Pacific region. In September 2016, an article in The Economic Times [7] stated that Jamie Dimon, Chairman of JP Morgan, identified Indian economy as the “sole bright spot” in the ongoing period of global uncertainty. Hiremath [8] stated that the importance of Indian stock market was growing at the global level which was evident from its rising market capitalization to gross domestic product (GDP) ratio and its rising integration with the world economy. Referring to the S&P Fact Book, Hiremath [8] stated that the Indian stock markets had the highest number of listed companies in the world. National Stock Exchange (NSE) [9] stated, “Following the implementation of reforms in the securities industry in the past few years, Indian stock markets have stood out in the global ranking”.
This paper thus aims to address this “relatively dormant” area and investigate the PEAD effect in the Indian stock market, one of the most important emerging markets at the global level and specifically at Asia-Pacific level.
2. Literature Review
Ever since the discovery of the anomaly by Ball and Brown [5] in context of the US stock market, evidences in support of its presence have been reported by Rendleman Jr., et al. [10] , Foster et al. [11] , Bernard and Thomas [12] , Bhushan [13] , Zhang [14] for US; Liu et al. [15] for the UK; Forner et al. [16] for Spain; Sen [17] , Sehgal and Bijoy [18] for India; Chudek et al. [19] for Canada; Truong [6] for China; Swart and Hoffman [20] for South Africa; and Forbes and Giannopoulos [21] for Greece. Studies which did not report the presence of SUE effect include Reinganum [22] for US; Sharma and Chander [23] for India. Truong [6] presents a decent review of significant works on this anomaly across different stock markets globally. Apart from country level studies, literature survey on the anomaly has been authored by Ball [24] . In literature, the PEAD anomaly has also been referred to as the standardized unexpected earnings (SUE effect) or the earnings momentum anomaly or the earnings surprise anomaly.
While majority of the studies agree on presence of robust PEAD anomaly for different markets, they fail to agree on probable explanations. Various reasons have been proposed in literature for explaining the presence of PEAD phenomenon. Bernard and Thomas [12] explored the possibility of each of the arguments put forth in literature to identify the most suitable reason.
Number of papers calculated earnings surprise based on asset pricing models: Ball [24] argued that the PEAD anomaly was a result of either incompleteness of the Capital Asset Pricing Model (CAPM) or its inappropriate implementation, the former being a more possible explanation. On the contrary, Rendleman Jr., et al. [10] reported that risk adjustment was of little significance while analyzing the SUE effect. Foster et al. [11] contended that the phenomenon was evident only for a subset of models employed for calculating expected earnings. The authors also contended that earnings forecast error exhibited high collinearity with the firm size. Kim and Kim [25] supported the argument of model misspecification, whereas Bernard and Thomas [12] and Bernard and Seyhun [26] did not find evidence to support the same. Bartov [27] contended that the anomaly was caused because the market failed to incorporate the time-series properties of earnings correctly while estimating expected earnings.
Another class of researchers attributed this phenomenon to delayed response. The delay, further, was manifested into different forms. Bhushan [13] argued that a significant proportion of drift was due to transactions costs―the author reported that the PEAD was inversely related to direct and indirect trading cost (proxy share price and dollar trading volume, respectively) and these relationships also captured the inverse relationship between PEAD and firm size. Transaction costs as probable explanation had also been supported by Asthana [28] , Ng et al. [29] and Chordia et al. [30] . Chordia et al. [30] reported that the anomaly was primarily limited to highly illiquid stocks. Bernard and Thomas [12] reported that while transaction costs could not be fully justified as probable explanation, delayed price response on part of traders seemed a viable explanation. Hirshleifer et al. [31] contended that the delayed response was caused by investor distraction hypothesis―investors got distracted by a large number of earnings announcement from several firms, which led to delayed response. Investor inattention as possible explanation had been argued by Dellavigna and Pollet [32] . Limits to arbitrage as a possible explanation had been supported by Chung and Hrazdil [33] . Jones and Litzenberger [34] believed that upon earnings announcement, a positive earnings surprise aroused interest of professional investors in the stocks, which led to positive drift and the drift persisted because the positive outlook gradually disseminated in general investors. Zhang [14] argued that lack of responsiveness on part of stock analysts contributed towards PEAD anomaly. The author reported that the more promptly analysts revised their forecasts for future earnings to incorporate new information, the lesser was PEAD. Chordia and Shivakumar [35] and Basu et al. [36] contended that incomplete assimilation of macroeconomic information (especially inflation) by analysts and investors while forecasting earnings could partially explain the phenomenon. Asthana [28] and Fricke et al. [37] contended that the phenomenon was a result of information asymmetry and timelier information dissemination to larger mass could reduce the anomaly.
The PEAD phenomenon is often termed as the “granddaddy” in the context of anomalies and is also believed to be one of the most researched accounting anomalies [19] . As already stated, the paper aims to test this anomaly in the less-researched Indian stock market.
3. Objective, Data and Methodology
The objective of the paper is to test the presence of PEAD anomaly in the Indian stock market. The scope of the study is Nifty 500 companies and the study stretches over a period of 2002 (quarter 4) to 2017 (quarter 3). The date of sample selection is 31 March 2014. The data sources employed are Ace Equity®, Reserve Bank of India website and websites of companies.
The methodology can be summarized in a series of steps as defined below:
Step 1: Every quarter, stocks are sorted on the basis of SUE, and divided into 10 portfolios.
Standardized unexpected earnings is defined as the unexpected earnings standardized using a suitable variable. Unexpected earnings is the difference between actual earnings announced by a firm and the earnings that they were expected to announce.
In this study, the actual earnings of a firm announced in the same quarter last fiscal is taken as the proxy for the expected earnings every quarter. Similar proxy has been chosen in literature by Livnat and Mendenhall [38] , Shivakumar [39] , Chudek et al. [19] , Truong [6] , Cao and Narayanamoorthy [40] and Zhang et al. [41] . Stock price has been taken as the scaling variable, which is also the scaling variable in studies by Livnat and Mendenhall [38] , Chudek et al. [19] , Truong (2011) [6] and Hung et al. [42] . Classification into 10 portfolios based on SUE has also been adopted by Foster et al. [11] .
Thus, SUE can be represented mathematically as follows:
(1)
Here,
is the SUE of stock i relative to earnings announcement e;
is the earnings per share of stock i in the announcement e;
is the earnings per share of stock i in the announcement e − 4;
is the price of stock i at time t relative to earnings announcement e.
In this study, following Hung et al. [42] , stock price at least 6 but not more than 12 days before the earnings announcement is employed. Portfolios are created using decile values as the break-points. Out of the valid records, 1 per cent of the cases are trimmed from both the extremes to exclude outliers. Trimming as a tool has been supported by Fabozzi et al. [43] .
Step 2: Every quarter, PEAD is calculated for every stock, and then averaged across stocks of each portfolio.
PEAD is measured as the buy-and-hold return on a stock in excess of buy-and-hold return on the proxy for market portfolio over the same period. This measure has been adopted in literature by Chudek et al. [19] , Truong [6] and Hung et al. [42] . In terms of equation, PEAD can be presented as follows:
(2)
Here,
is the PEAD for stock i relative to earnings announcement e;
is the return on stock i relative to earnings announcement e at time t;
is the return on proxy of market portfolio relative to respective stock’s earnings announcement e at time t.
Following Hung et al. [42] , buy-and-hold return is calculated over a period of day +2 to +64 relative to earnings announcement. Referring to work of Berkman and Truong [6] on the US market that suggested calculation of PEAD from day +2 to avoid contemporaneous stock price reaction, Truong [6] followed the practice for other market as a conservative approach. Only the stocks that possess at least 44 non-zero returns figure during day +2 to +64 form part of the analysis. This practice is adopted from the work of Hung et al. [42] . Out of the valid records, 1 per cent of the cases are trimmed from both the extremes to exclude outliers.
Step 3: The PEAD on extreme portfolios are compared to see if they are statistically different in magnitude.
For every portfolio, Step 1 and 2 lead to time-series of quarterly PEADs. To test if the differences in average PEAD across portfolios are statistically significant, the PEAD on extreme portfolios are compared using paired t-test. A statistically significant difference would indicate that the magnitude of PEAD is not equal across portfolios of stocks with varying magnitude of SUE.
Step 4: Regressing PEAD on SUE: To test if the long-short investment strategy involving extreme portfolios generate statistically significant returns, PEAD is regressed on coded SUE measure.
Every quarter, SUEs for individual stocks are ranked on the basis of their magnitude and then converted into codes ranging from 0 to 1. The codes are further modified by subtracting 0.5 from each of them, resulting into a modified code ranging from −0.5 to 0.5. Using the modified codes thus obtained, Fama and MacBeth [1] regression is applied: PEAD is regressed on the coded SUEs.
The practice of modified coding is adopted in literature by Chudek et al. [19] and Truong [6] . The authors contend that coding from 0 to 1 resolves the problems of potential non-linearity in the PEAD-SUE relation. Further, modifying the codes to the range of −0.5 to 0.5 has following implications: Every quarter, the stock with the median SUE would be coded close to zero. Therefore, the intercept of the regression would exhibit the average PEAD earned by the median placed stock. Further, the gradient (or the SUE coefficient) would exhibit the difference between average PEAD earned by the highest and the lowest placed stocks.
Following literature [6] [19] , Fama and MacBeth regression [1] is employed. The process is defined as follows―the regression is applied separately for every quarter at the stock level data. The coefficients thus obtained every quarter are then averaged over the study period to obtain one final coefficient for the entire exercise. The equation employed is:
(3)
Here,
is the PEAD for stock i;
and are regression coefficients (intercept and gradient respectively);
is the SUE for stock i.
The SUE coefficient represents the average PEAD earned by going long on the highest SUE generating stocks and going short on the lowest SUE generating stocks. Statistically significant coefficient implies that such investment strategy would generate significant returns in statistical sense.
The t-statistic is computed using the following formula:
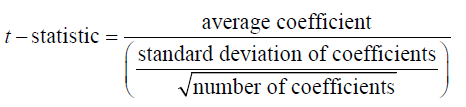 (4)
(4)
The denominator employed in the equation is also termed as the standard error.
Step 5: To test if the SUE anomaly is statistically affected by the inclusion of other variables under study, PEAD is regressed on coded SUE with additional explanatory variables in the model.
Other variables treated as control variables include the following:
Beta: It is estimated using market model on data of 250 days prior to earnings announcement. Same practice is adopted in literature by Hung et al. [42] . The model is as defined below:
(5)
Here,
is the excess return for stock i at time t;
is the return on stock i at time t;
is the return on proxy for risk-free security at time t. 91-day Treasury bills are chosen as the risk-free security and their yields are employed as the measure of risk-free returns;
and are the regression coefficient (intercept and gradient respectively);
is the market risk premium. It measures excess return on proxy for market portfolio at time t;
is the return on market portfolio at time t. Nifty 500 index is chosen as the proxy for market portfolio and its returns are deemed to be returns on market portfolio;
is the residual/error/disturbance term.
Size: Market capitalization is chosen as the measure of size. It is defined as the product of closing prices and number of shares outstanding. Same practice is adopted in literature by Truong [6] and Hung et al. [42] . The measure is estimated as follows:
(6)
Market capitalization is computed every year at September-end and is assumed to remain constant for one year. It is based on number of paid-up equity shares as at March-end and closing prices as at September-end of the same year. It is customary in literature to employ six months gap between fiscal year-end and computation of variables [44] [45] [46] . This is to avoid look-ahead bias1 and ensure that the variables are known at the time of computation.
Value: The ratio of market price to book value (P/B ratio) is chosen as the measure of value. Same practice is adopted in literature by Truong [6] and Hung et al. [42] . Only the records with positive adjusted book values are considered. The employed formula is as follows:
(7)
Here, book value is defined as equity paid-up + reserves and surplus ? revaluation reserve ? miscellaneous expenses not written-off. Analogous to the approach adopted for computation of market capitalization, P/B ratio is computed every year at September-end and is assumed to remain constant for one year. All the input values are as at March-end every year.
1“The look-ahead bias occurs when the researcher uses data not yet available to the investor, i.e., using December net income in January when it is not available to investors until several months later” [47] . Jacobs and Levy (1988) [48] attributed this bias to announcement lags.
Liquidity: Amihud [49] illiquidity measure (AI) is chosen as the proxy for liquidity. It is estimated over a period of −252 to −2 days relative to earnings announcement. Same practice is adopted in literature by Hung et al. [42] . It is defined as the average ratio of daily absolute returns to the daily trading volume in terms of Indian National Rupee (INR). It measures the change in price for each unit of change in rupee trading volume. A higher AI value would represent more illiquidity. The measure can be represented mathematically by the following eq uation:
(8)
Here,
is illiquidity for stock i during time t;
is number of days with available trading data for stock i during time t;
is the return on stock i on day d of time t;
is the trading volume (in terms of INR) of stock i on day d of time t.
Arbitrage risk: Idiosyncratic volatility is chosen as the proxy for arbitrage risk. It is calculated as the standard deviation of the residuals from the market model. Similar to the practice employed by Hung et al. [42] , the model is estimated using data from −252 to −2 days.
For each control variable, 1 per cent of the overall valid cases are trimmed from both the extremes to exclude outliers. Similar to the approach adopted under the SUE effect anomaly, the control variables are also converted into modified codes ranging from −0.5 to 0.5.
Using the modified codes thus obtained, Fama and MacBeth [1] regression is applied: PEAD is regressed on the coded SUEs and other coded explanatory variables. The regression is applied separately for every quarter at the stock level data. The coefficients thus obtained every quarter are then averaged over the study period to obtain one final coefficient for the entire exercise. The equation employed is:
(9)
Here,
to are regression coefficients (gradients)
, , , and are interaction variables for stock i derived from interaction of SUE with the control variables.
The coefficients of interaction variables exhibit incremental contribution of control variables on the PEAD-SUE relation. For example, ω2 represents the difference between PEAD generated by stocks with the extreme SUE codes, when only the stocks with extreme beta codes are considered. Similar interpretation is applicable for coefficients of other interaction variables. Statistically significant coefficient of any interaction variable implies that PEAD-SUE relation varies significantly for the underlying control variable. For example, statistically significant ω2 would imply that the PEAD-SUE relation is significantly different for stocks with different betas. In other words, beta has incremental effect on PEAD-SUE relation. Similar interpretation is applicable for coefficients of other interaction variables.
Robustness test:
Sub-period analysis is undertaken as a test for robustness. The study period is divided into two sub-periods and tests are re-employed on each sub-period. 2008 has been chosen as the year for splitting data. The rationale behind choosing this year is that it is considered as the year of world financial crisis [50] . NSE [9] also defined 2008 as the year of global financial crisis. Similar to the approach adopted for this study, October 2008 has also been chosen as the breakpoint by Minovic and Zivkovic [51] . The selection would serve two purposes. Apart from testing the robustness, the analysis would also highlight the impact of the crisis on the Indian stock market.
The method of sub-period analysis as a tool for robustness test has been adopted in literature by Jiang [52] , Lam and Tam [53] , Truong [6] and Assefa and Mollick [50] . It has been employed as a tool to compare the before-and-after situation by Yang [54] . Batten and Vo [55] stated that the level of global market integration changed over time and was likely to be affected by events such as global financial crisis. The level of global market integration could, in turn, define the benefits of international diversification and thus affect the level of premiums that the investors expected to earn for risk factors. Thus, there is a fair possibility of difference in the expectations of the investors in the two sub-periods.
4. Analysis
Table 1 summarizes the time series averages of PEAD earned by SUE sorted portfolios. Portfolio P1 represents firms with the lowest SUE while P10 represents firms with the highest SUE. The magnitude of SUE increases as one moves from P1 to P10. Figure 1 graphically presents the information contained in Table 1. For the study period as a whole, there appears a positive association between PEAD and SUE. With an increase in SUE, the drift also increases. For portfolio P1, the average drift is −0.014, which for portfolio P10 is 0.034. The difference of 0.048 is statistically significant at 1 per cent level. For sub-period 1 of the study, the positive relation between SUE and PEAD persists. P1 generates an average PEAD of −0.027, while P10 generates 0.030―the difference, 0.057, being statistically significant at 1 per cent level. For sub-period 2 of the study as well, there exists a positive relation between PEAD and SUE. On an average, P1 generates PEAD of −0.005, while P10 generates PEAD of 0.037. Yet again, the difference of 0.042 is statistically significant at 1 per cent level. Thus, overall, there is a positive relation between SUE and PEAD in the Indian stock market. Moreover, the relation is robust to changing the period of study. Significant positive relation is reported for all the three study periods under consideration.
Giving further credence to the findings of Table 1, Table 2 (columns II and III) exhibits that for all the three study periods, regressing PEAD on coded SUE generates statistically significant slope coefficients. For the whole study period, the value is 0.06. While it is 0.07 for sub-period 1, it is 0.05 for sub-period 2. All the three are statistically significant at 1 per cent level. This implies that during all the study periods, the investment strategy of going long on the stocks with the highest SUE codes and going short on the stocks with the lowest SUE codes
Table 1. Time series average of PEAD on SUE sorted portfolios (2002-2017).
Note: ***signifies significance at 1 per cent level; figures in brackets exhibit negative numbers.
Table 2. Regression of PEAD on SUE and control variables (2002-2017).
Note: Figures in brackets exhibit negative numbers. ***depicts significance at 1% level, **depicts significance at 5% level, *depicts significance at 10% level.
generates statistically significant returns. For the whole study period, the stocks with the highest coded SUEs generate 6 per cent higher PEAD than the stocks with the lowest coded SUEs over 64 days post the announcement. The corresponding figures for sub-period 1 and sub-period 2 are 7 per cent and 5 per cent respectively. The intercept for the whole study period is 0.01, which is
Figure 1. Time series average of PEAD on SUE sorted portfolios (2002-2017). The figure exhibits the average PEAD generated by 10 SUE sorted portfolios for the three study periods under consideration (2002-2017, 2002-2008 and 2008-2017). The horizontal axis represents 10 portfolios―P1 is the portfolios with the lowest SUE stocks and P10 is the portfolio with the highest SUE stocks. SUE rises from P1 to P10. The vertical axis represents the average PEAD. It ranges from −0.027 to 0.037.
statistically significant at 10 per cent level. This implies that the stocks with median SUE codes (close to zero) also earn statistically significant PEAD of 1 per cent. Though the intercept in sub-period 1 is also 0.01, it is statistically insignificant. This implies that during sub-period 1, stocks with coded SUE close to zero did not earn PEAD statistically different from zero. However, the intercept becomes statistically significant during sub-period 2―with a value of 0.02, it is significant at 5 per cent level.
Table 2 (columns IV and V) also reports the impact on SUE on introduction of other variables. The columns report the results for regressing PEAD on coded SUE and other control variables. As is evident, the control variables employed in the regression are interaction variables. For the whole study period, referring to columns IV and V, the intercept term, 0.01, is statistically significant at 5 per cent level. This implies that the stocks with median coded SUE generate statistically significant PEAD of 1 per cent. The coefficient for SUE is 0.05, which is statistically significant at 1 per cent level. This implies that the SUE effect does not lose significance even after controlling for variables like beta, size, value, liquidity and arbitrage risk. The coefficient for the interaction variable SUE X Value is 0.07, which is statistically significant at 1 per cent level. This implies that the SUE effect is enhanced in the high P/B ratio stocks. The figure 0.07 implies that the difference between PEAD observed for stocks with high coded SUE and low coded SUE is 7 per cent higher in stocks with high coded P/B ratio than in stocks with low coded P/B ratio. The coefficient for SUE X Beta is −0.05, which is statistically significant at 10 per cent level. This implies that the difference between PEAD observed for stocks with high coded SUE and low coded SUE is 5 per cent higher in stocks with low coded betas than in stocks with high coded betas. The coefficients of other control variables (interaction variables with size, illiquidity and arbitrage risk) are statistically insignificant. This implies that the difference between SUE effect across stocks varying on these aspects (i.e., varying in size, illiquidity or arbitrage risk) is not significant statistically.
The findings and interpretations are almost similar in sub-period 1 of the study. Unlike the whole study period, the intercept is statistically insignificant. However, similar to the findings of whole study period, coefficients of both SUE (0.06) and SUE X Value (0.13) are statistically significant. SUE X Beta records a coefficient of −0.15, which is statistically stronger than for the whole study period (significant at 5 per cent level).
The findings of sub-period 2 are relatively different from the other two periods under study. While the coefficient of SUE (0.04), similar to other two study periods, is significant at 1 per cent level and the period exhibits a statistically significant intercept of 0.02 (significant at 5 per cent), the behavior of interaction variables vary. SUE X Size exhibits a statistically significant coefficient of −0.06 (significant at 5 per cent). This implies that the difference between PEAD observed for stocks with high coded SUE and low coded SUE is 6 per cent higher in stocks with low coded size than in stocks with high coded size. None of the other control variables generate statistically significant coefficients.
Thus, overall, the SUE effect is significant and is robust across sub-periods. While the interaction variable SUE X Value and SUE X Beta are significant in whole study period and sub-period 1, SUE X Size becomes significant in sub-period 2. None of the other interaction variables exhibit statistical significance in enhancing the SUE effect.
5. Findings
For the SUE sorted portfolios, paired t-test reveals that the returns generated by the portfolio with the highest negative drifts (which are negative) are statistically lower than the returns generated by the portfolio with the highest positive drifts (which are positive). Overall, across the 10 portfolios, a positive association between the magnitude and sign of SUE and drift is evident. The relationship is robust to sub-period analysis, as similar results are evident during both the sub-periods under study. These findings reveal the presence of robust PEAD anomaly in the Indian stock market. The findings are similar to those reported for other countries―Canada [19] , China [6] , Greece [21] , South Africa [20] , Spain [16] and UK [15] . For the Indian stock market, similar findings are reported by Sen [17] and Sehgal and Bijoy [18] . This study provides an update on the anomaly employing more recent and longer study period.
On regressing PEAD on SUE, the coefficient exhibits a value of 0.06, which implies that the investment strategy of going long on the stocks with the highest SUE codes and going short on the stocks with the lowest SUE codes generates statistically significant returns of 6 per cent during 64 days post the earnings announcement. In literature, for similar analysis, the reported results are 4.11 per cent in Chinese stock market [6] and 6 per cent in Canadian stock market [19] . This is perhaps an indication that the magnitude of drift observed in Canada is almost similar to that observed in India. On the other hand, though the anomaly is reported in Chinese stock market, the magnitude is lesser than in Indian market. International investors can find this information useful to choose their investment destination. By adopting the same investment strategy, investors can probably reap higher returns in India (and Canada) than in China.
Even after introduction of other control variables in the regression model, the significance of SUE effect remains. This is similar to the findings reported by Truong [6] who reported that this phenomenon was not a manifestation of relation between returns and other variables (employed as control variables in the study).
For the overall study period, the PEAD effect is enhanced in stocks with higher P/B ratios and the effect decreases with increase in beta. The findings are similar during the period 2002-2008. However, period 2008-2017 reveals that the anomaly is enhanced for stocks with lower market capitalization. That magnitude of PEAD varies between value and growth stocks has been highlighted by Yan and Zhao [56] . Inverse relationship between size and PEAD has also been highlighted by Bernard and Thomas [12] , Bhushan [13] and Swart and Hoffman [20] .
The study has important implications for investors and regulators.
Implication for investors: Bodie et al. [3] stated, “… even in environments as competitive as the financial markets, we may observe only near-efficiency, and profit opportunities may exist for especially diligent and creative investors”. Investors can benefit from the findings by designing their investment strategies taking into consideration the PEAD anomaly. An investor would do well if she/he purchases the stocks with extreme positive standardized unexpected earnings and short sells the stocks with extreme negative SUEs, hold them for 64 days and square off their positions at the end of the period.
Implication for regulators: Policy makers and regulators are interested in knowing the anomalous areas operating in the stock markets. The National Stock Exchange (NSE) [9] stated that the regulatory bodies in India had, as one of the objectives, to maintain fair, transparent and efficient markets. Jaisinghani [57] stated that it was desirable for regulators to learn if there were certain market microstructures or regulatory inefficiencies that drove anomalies so that necessary actions could be taken to improve market efficiency. By providing an update on the PEAD anomaly, this study aids the regulators in identifying an area that they might need to concentrate their efforts on.
6. Conclusions
Over a period of 2002 to 2017, the paper studies the Indian stock market and reports the presence of statistically significant PEAD anomaly―the stocks with negative earnings surprise drift negatively and the ones with positive earnings surprise drift positively during the span of 64 days post the announcement of earnings. The anomaly is robust to inclusion of other variables (viz., beta, market capitalization, P/B ratio, illiquidity and idiosyncratic volatility) and to sub-period analysis. While the presence of anomaly had been reported in literature for other countries, the study adds the evidence for the Indian stock market. Thus, by providing an input for possible investment window and exhibiting evidence of corroborative returns, the paper is able to provide a possible investment strategy to investors looking to exploit the PEAD anomaly in India. On the other hand, for market regulators, the findings can act as inputs to know the current state of market efficiency and thereby design their strategy accordingly to achieve higher level of efficiency.
2As on 31 March 2014, the index represented 97 per cent of the free float market capitalization of the stocks listed on the NSE [58] .
While the article endeavors to address the dearth in literature by studying the PEAD anomaly in the Indian stock market, it has its limitations which pave the path for future research directions. First, the article is based on the constituent companies of Nifty 500 index. While the companies fairly represent the Indian stock market2, they are by no means exhaustive and a more comprehensive study can be undertaken incorporating broader base of companies. Further, while this article analyses the drift over a period of 64 days post the earnings announcement, analyses can be conducted for other durations as well.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Harshita, Singh, S. and Yadav, S.S. (2018) Post-Earnings- Announcement Drift Anomaly in India: A Test of Market Efficiency. Theoretical Economics Letters, 8, 3178-3195. https://doi.org/10.4236/tel.2018.814197
References
- 1. Fama, E.F. and MacBeth, J.D. (1973) Risk, Return, and Equilibrium: Empirical Tests. The Journal of Political Economy, 81, 607-636. https://doi.org/10.1086/260061
- 2. Lo, A.W. (2007) Efficient Market Hypothesis. In: Blume, L. and Durlauf, S., Eds., The New Palgrave: A Dictionary of Economics, Palgrave McMillan, New York, 1-28.
- 3. Bodie, Z., Kane, A., Marcus, A.J. and Mohanty, P. (2013) Investments. McGraw-Hill Education (India) Pvt. Ltd., New Delhi.
- 4. Fama, E.F. (1970) Efficient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance, 25, 383-417. https://doi.org/10.2307/2325486
- 5. Ball, R. and Brown, P. (1968) An Empirical Evaluation of Accounting Income Numbers. Journal of Accounting Research, 6, 159-178. https://doi.org/10.2307/2490232
- 6. Truong, C. (2011) Post-Earnings Announcement Abnormal Return in the Chinese Equity Market. Journal of International Financial Markets, Institutions and Money, 21, 637-661. https://doi.org/10.1016/j.intfin.2011.04.002
- 7. The Economic Times (2016) Not an Exaggeration to Call India Sole Bright Spot: JPMorgan Chairman Jamie Dimon. http://economictimes.indiatimes.com/markets/expert-view/not-an-exaggeration-to-call-india-sole-bright-spot-jpmorgan-chairman-jamie-dimon/articleshow/54398435.cms
- 8. Hiremath, G.S. (2014) Indian Stock Market: An Empirical Analysis of Informational Efficiency. Springer Briefs in Economics, New Delhi.
- 9. National Stock Exchange of India Limited (2015) Indian Securities Market: A Review. http://www.nseindia.com/research/dynaContent/ismr.htm
- 10. Rendleman Jr., R.J., Jones, C.P. and Latane, H.A. (1982) Empirical Anomalies Based on Unexpected Earnings and the Importance of Risk Adjustments. Journal of Financial Economics, 10, 269-287. https://doi.org/10.1016/0304-405X(82)90003-4
- 11. Foster, G., Olsen, C. and Shevlin, T. (1984) Earnings Releases, Anomalies, and the Behavior of Security Returns. The Accounting Review, 59, 574-603.
- 12. Bernard, V.L. and Thomas, J.K. (1989) Post-Earnings-Announcement Drift: Delayed Price Response or Risk Premium? Journal of Accounting Research, 27, 1-36. https://doi.org/10.2307/2491062
- 13. Bhushan, R. (1994) An Informational Efficiency Perspective on the Post-Earnings Announcement Drift. Journal of Accounting and Economics, 18, 45-65. https://doi.org/10.1016/0165-4101(94)90018-3
- 14. Zhang, Y. (2008) Analyst Responsiveness and the Post-Earnings-Announcement Drift. Journal of Accounting and Economics, 46, 201-215. https://doi.org/10.1016/j.jacceco.2008.04.004
- 15. Liu, W., Strong, N. and Xu, X. (2003) Post-Earnings-Announcement Drift in the UK. European Financial Management, 9, 89-116. https://doi.org/10.1111/1468-036X.00209
- 16. Forner, C., Sanabria, S. and Marhuenda, J. (2009) Post-Earnings Announcement Drift: Spanish Evidence. Spanish Economic Review, 11, 207-241. https://doi.org/10.1007/s10108-008-9048-4
- 17. Sen, K. (2009) Earnings Surprise and Sophisticated Investor Preferences in India. Journal of Contemporary Accounting & Economics, 5, 1-19. https://doi.org/10.1016/j.jcae.2008.11.001
- 18. Sehgal, S. and Bijoy, K. (2015) Stock Price Reactions to Earnings Announcements: Evidence from India. Vision: The Journal of Business Perspective, 19, 25-36. https://doi.org/10.1177/0972262914564042
- 19. Chudek, M., Truong, C. and Veeraraghavan, M. (2011) Is Trading on Earnings Surprises a Profitable Strategy? Canadian Evidence. Journal of International Financial Markets, Institutions & Money, 21, 832-850. https://doi.org/10.1016/j.intfin.2011.06.004
- 20. Swart, D.J. and Hoffman, A.J. (2013) Analysis of the Post-Earnings Announcement Drift Anomaly on the JSE. Investment Analysts Journal, 42, 17-34. https://doi.org/10.1080/10293523.2013.11082553
- 21. Forbes, W. and Giannopoulos, G. (2015) Post-Earnings Announcement Drift in Greece. Review of Pacific Basin Financial Markets and Policies, 18, Article ID: 1550019.
- 22. Reinganum, M.R. (1981) Misspecification of Capital Asset Pricing: Empirical Anomalies Based on Earnings’ Yields and Market Values. Journal of Financial Economics, 9, 19-46. https://doi.org/10.1016/0304-405X(81)90019-2
- 23. Sharma, R. and Chander, R. (2009) Earnings Announcements and Stock Price Behavior on Indian Stock Markets. Asia Pacific Business Review, 5, 117-126. https://doi.org/10.1177/097324700900500313
- 24. Ball, R. (1978) Anomalies in Relationships between Securities’ Yields and Yield-Surrogates. Journal of Financial Economics, 6, 103-126. https://doi.org/10.1016/0304-405X(78)90026-0
- 25. Kim, D. and Kim, M. (2003) A Multifactor Explanation of Post-Earnings Announcement Drift. Journal of Financial and Quantitative Analysis, 38, 383-398. https://doi.org/10.2307/4126756
- 26. Bernard, V.L. and Seyhun, H.N. (1997) Does Post-Earnings-Announcement Drift in Stock Prices Reflect a Market Inefficiency? A Stochastic Dominance Approach. Review of Quantitative Finance and Accounting, 9, 17-34. https://doi.org/10.1023/A:1008245709673
- 27. Bartov, E. (1992) Patterns in Unexpected Earnings as an Explanation for Post-Announcement Drift. The Accounting Review, 67, 610-622.
- 28. Asthana, S. (2003) Impact of Information Technology on Post-Earnings Announcement Drift. Journal of Information Systems, 17, 1-17. https://doi.org/10.2308/jis.2003.17.1.1
- 29. Ng, J., Rusticus, T.O. and Verdi, R.S. (2008) Implications of Transaction Costs for the Post-Earnings Announcement Drift. Journal of Accounting Research, 46, 661-696. https://doi.org/10.1111/j.1475-679X.2008.00290.x
- 30. Chordia, T., Goyal, A., Sadka, G., Sadka, R. and Shivakumar, L. (2009) Liquidity and the Post-Earnings-Announcement Drift. Financial Analysts Journal, 65, 18-32. https://doi.org/10.2469/faj.v65.n4.3
- 31. Hirshleifer, D., Lim, S.S. and Teoh, S.H. (2009) Driven to Distraction: Extraneous Events and Underreaction to Earnings News. The Journal of Finance, 64, 2289-2325. https://doi.org/10.1111/j.1540-6261.2009.01501.x
- 32. Dellavigna, S. and Pollet, J.M. (2009) Investor Inattention and Friday Earnings Announcements. The Journal of Finance, 64, 709-749. https://doi.org/10.1111/j.1540-6261.2009.01447.x
- 33. Chung, D.Y. and Hrazdil, K. (2011) Market Efficiency and the Post-Earnings Announcement Drift. Contemporary Accounting Research, 28, 926-956. https://doi.org/10.1111/j.1911-3846.2011.01078.x
- 34. Jones, C.P. and Litzenberger, R.H. (1970) Quarterly Earnings Reports and Intermediate Stock Price Trends. The Journal of Finance, 25, 143-148. https://doi.org/10.1111/j.1540-6261.1970.tb00420.x
- 35. Chordia, T. and Shivakumar, L. (2005) Inflation Illusion and Post-Earnings-Announcement Drift. Journal of Accounting Research, 43, 521-556. https://doi.org/10.1111/j.1475-679X.2005.00181.x
- 36. Basu, S., Markov, S. and Shivakumar, L. (2010) Inflation, Earnings Forecasts, and Post-Earnings Announcement Drift. Review of Accounting Studies, 15, 403-440. https://doi.org/10.1007/s11142-009-9112-9
- 37. Fricke, E., Fung, S. and Goktan, M.S. (2014) Google Search, Information Uncertainty, and Post-Earnings Announcement Drift. Journal of Accounting and Finance, 14, 11-27.
- 38. Livnat, J. and Mendenhall, R.R. (2006) Comparing the Post-Earnings Announcement Drift for Surprises Calculated from Analyst and Time Series Forecasts. Journal of Accounting Research, 44, 177-205. https://doi.org/10.1111/j.1475-679X.2006.00196.x
- 39. Shivakumar, L. (2006) Accruals, Cash Flows and the Post-Earnings-Announcement drift. Journal of Business Finance & Accounting, 33, 1-25.
- 40. Cao, S.S. and Narayanamoorthy, G.S. (2012) Earnings Volatility, Post-Earnings Announcement Drift, and Trading Frictions. Journal of Accounting Research, 50, 41-74. https://doi.org/10.1111/j.1475-679X.2011.00425.x
- 41. Zhang, Q., Cai, C.X. and Keasey, K. (2014) The Profitability, Costs and Systematic Risk of the Post-Earnings-Announcement-Drift Trading Strategy. Review of Quantitative Finance and Accounting, 43, 605-625. https://doi.org/10.1007/s11156-013-0386-4
- 42. Hung, M., Li, X. and Wang, S. (2015) Post-Earnings-Announcement Drift in Global Markets: Evidence from an Information Shock. The Review of Financial Studies, 28, 1242-1283. https://doi.org/10.1093/rfs/hhu092
- 43. Fabozzi, F.J., Focardi, S.M. and Kolm, P.N. (2010) Quantitative Equity Investing: Techniques and Strategies. John Wiley & Sons, Inc., New Jersey.
- 44. Lam, K.S.K. (2002) The Relationship between Size, Book-to-Market Equity Ratio, Earnings-Price Ratio, and Return for the Hong Kong Stock Market. Global Finance Journal, 13, 163-179. https://doi.org/10.1016/S1044-0283(02)00049-2
- 45. Yen, J.Y., Sun, Q. and Yan, Y. (2004) Value versus Growth Stocks in Singapore. Journal of Multinational Financial Management, 14, 19-34. https://doi.org/10.1016/S1042-444X(03)00036-7
- 46. Das, S. and Barai, P. (2016) Size, Value and Momentum in Stock Returns: Evidence from India. Macroeconomics and Finance in Emerging Market Economies, 9, 284-302. https://doi.org/10.1080/17520843.2016.1148754
- 47. Jaffe, J., Keim, D.B. and Westerfield, R. (1989) Earnings Yields, Market Values, and Stock Returns. The Journal of Finance, 44, 135-148. https://doi.org/10.1111/j.1540-6261.1989.tb02408.x
- 48. Jacobs, B.I. and Levy, K.N. (1988) Disentangling Equity Return Regularities: New Insights and Investment Opportunities. Financial Analysts Journal, 44, 18-43. https://doi.org/10.2469/faj.v44.n3.18
- 49. Amihud, Y. (2002) Illiquidity and Stock Returns: Cross-Section and Time-Series Effects. Journal of Financial Markets, 5, 31-56. https://doi.org/10.1016/S1386-4181(01)00024-6
- 50. Assefa, T.A. and Mollick, A.V. (2014) African Stock Market Returns and Liquidity premia. Journal of International Financial Markets, Institutions & Money, 32, 325-342. https://doi.org/10.1016/j.intfin.2014.06.009
- 51. Minovic, J. and Zivkovic, B. (2014) CAPM Augmented with Liquidity and Size Premium in the Croatian Stock Market. Economic Research-Ekonomska Istrazivanja, 27, 191-206.
- 52. Jiang, L. (2011) Order Imbalance, Liquidity, and Market Efficiency: Evidence from the Chinese Stock Market. Managerial and Decision Economics, 32, 469-480. https://doi.org/10.1002/mde.1547
- 53. Lam, K.S.K. and Tam, L.H.K. (2011) Liquidity and Asset Pricing: Evidence from the Hong Kong Stock Market. Journal of Banking and Finance, 35, 2217-2230. https://doi.org/10.1016/j.jbankfin.2011.01.015
- 54. Yang, C. (2015) An Empirical Study of Liquidity and Return Autocorrelations in the Chinese Stock Market. Asia-Pacific Financial Markets, 22, 261-282. https://doi.org/10.1007/s10690-015-9203-5
- 55. Batten, J.A. and Vo, X.V. (2014) Liquidity and Return Relationships in an Emerging Market. Emerging Markets Finance and Trade, 50, 5-21. https://doi.org/10.2753/REE1540-496X500101
- 56. Yan, Z. and Zhao, Y. (2011) When Two Anomalies Meet: The Post-Earnings Announcement Drift and the Value-Glamour Anomaly. Financial Analysts Journal, 67, 46-60. https://doi.org/10.2469/faj.v67.n6.3
- 57. Jaisinghani, D. (2016) An Empirical Test of Calendar Anomalies for the Indian Securities Markets. South Asian Journal of Global Business Research, 5, 53-84. https://doi.org/10.1108/SAJGBR-07-2014-0050
- 58. National Stock Exchange of India Limited (2014) Factsheet CNX 500. https://www.nseindia.com/products/content/equities/indices/indices.htm



