Received 1 4 April 2016; accepted 12 June 2016; published 15 June 2016

ABSTRACT

By making use of a geometry of preferences, Abe (2012) proves the Gul and Pesendorfer’s utility representation theorem about temptation without self-control. This companion paper provides a similar proof for the Gul and Pesendorfer's utility representation theorem about temptation and costly self-control. As a result, the both theorems are proved in the unified way.

Keywords:

Temptation, Self-Control, Utility Representation, Geometric Approach

1. Introduction

There is a large and growing literature on temptation and self-control in economics [1] [2] . Gul and Pesendorfer [3] propose basic models of choice under temptation and provide preference foundations for the models. We provide an alternative proof of the main theorem in [3] , that is, the Gul and Pesendorfer’s utility representation theorem about temptation and costly self-control. The proof makes use of a geometry of preferences and goes as follows. We first extract behaviors that display temptation and self-control. We then characterize the intuitive notions of temptation and self-control geometrically. Finally, we prove the utility representation theorem using the characterization. The proof highlights the reason why the self-control part can be written by sum of commitment utility and temptation utility. The proof also provides the refined testable implications of the Gul and Pesendorfer model.

This geometric approach is taken by the companion paper, [4] , to prove the Gul and Pesendorfer’s utility representation theorem about temptation without self-control. As a result, we prove the two representation theorems by an intuitive and unified approach.

This paper is organized as follows. Section 2 summarizes the Gul and Pesendorfer’s utility representation theorem. In Section 3, we explore our notions of temptation and self-control and derive those cone representations. Section 4 proves the Gul and Pesendorfer’s representation theorem using the result of Section 3. In Section 5, we discuss relation between our approach and the Gul and Pesendorfer’s approach.

2. The Gul and Pesendorfer Theorem

Let Z be a compact metric space of prizes. Let ∆ be the set of all Borel probability measures over Z and be endowed with the topology of weak convergence. Let 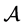be the set of all compact (with respect to the topology of weak convergence) subsets of ∆ and be endowed with the topology induced by the Hausdorff metric. For any 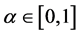and, we let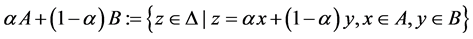. A typical element A of 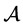is called a menu (of lotteries).

Let 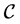be the set of continuous affine mappings from ∆ to real numbers; that is, if and only if f is continuous on ∆ and satisfies 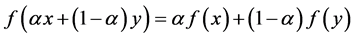for all 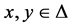and for all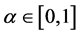. Throughout this paper, we say that f is cardinally equivalent to a function g when 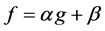for some positive 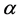and real.

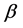We call the following model of utility function the Gul and Pesendorfer model.

Definition 1. A utility function U on menus is said to be a Gul and Pesendorfer model if it is a function of the form:

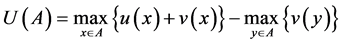(1)

for some.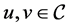

Gul and Pesendorfer [3] provided preference foundations for this model. Let be a binary relation over. We say that is

Ÿ upper semi-continuous if the sets are closed,

Ÿ lower semi-continuous if the sets are closed,

Ÿ continuous if it is upper and lower semi-continuous.

We consider the following axioms.

Axiom 1 (Preference). is a complete and transitive binary relation.

Axiom 2 (Continuity). is continuous.

Axiom 3 (Independence). and imply.

Axiom 4 (Set Betweenness). implies.

Axiom 1 is a standard revealed preference axiom. Axioms 2 and 3 are variants of the von Neumann and Morgenstern axioms adapted to the preferences-over-menus setting. Axioms 4 is viewed as intuitive notion of costly self-control behaviors under temptation as we explain below.

Imagine a situation in which an individual first chooses a menu and then selects an alternative from that menu. Suppose that the individual evaluates a menu by its best element. Such an individual's behavior is represented by a utility function U of the form for some. Observe that an individual with this type of utility function follows a regularity called Strategic Rationality: implies.¹ Clearly, any strategically rational decision maker does not exhibit a desire for commitment, where by `desire for commitment' we mean that an individual strictly prefers a subset of a menu to the menu itself.

Desire for commitment is an implication of temptation. An individual may strictly prefer menu A to menu to avoid succumbing to temptation that is anticipated as follows: The individual anticipates that he/she will be tempted to select an alternative when facing menu, and this alternative is undesired for him/her.

Axiom 4 relaxes Strategic Rationality and allows a possibility that. Suppose that B contains a tempting alternative. We can view as meaning that when facing menu, the individual uses self-control and can resist the temptation. We then interpret as meaning that exercising self-control is costly.

Gul and Pesendorfer [3] showed the following representation theorem.

Theorem 1. satisfies Preference, Continuity, Independence, and Set Betweenness if and only if it has a Gul and Pesendorfer representation, that is, there exists a Gul and Pesendorfer model U such that if and only if.

3. Geometry of Temptation and Self-Control

This section explores some geometric properties of that satisfies Set Betweenness (and von Neumann and Morgenstern type axioms). Specifically, as in [4] , we extract behaviors that display temptation and self-control and geometrically characterize the behaviors. All lemmas in this section are proved almost in the same way as Abe [4] and hence omitted.

Lemma 0. (Gul and Pesendorfer ( [4] , Lemma 1)). satisfies Preference, Continuity, and Independence if and only if there exists a continuous affine function that represents.^2,3

We define u by for all as in [3] . Since u represents preferences that the individual would like to commit to, it is called a commitment utility. Any commitment utility defined in this manner is continuous and affine from Lemma 0.

Consider a nontrivial preference relation, that is, there are such that. Set Betweenness induces the following four strict partial orders.⁴

Ÿ A weak temptation relation T is defined by if.

Ÿ A strong temptation relation is defined by if.

Ÿ A weak resistance relation R is defined by if.

Ÿ A strong resistance relation is defined by if.

Two temptation relations display a desire for commitment in a binary menu. Suppose. We view as meaning that the individual desires to commit to because y is more tempting than x. Two resistance relations display self-control. We view as meaning that the individual selects x when facing. This means that when y tempts him/her, he/she uses self-control and resists the temptation.

The next fact is worth pointing out, and we may use this fact repeatedly without warning below: When satisfies Set Betweenness, implies (i) exactly one of either or holds and (ii) exactly one of either or holds.

The following properties of four relations are the fundamentals for our geometric approach.

Lemma 1. Suppose that satisfies Preference, Continuity, Independence, and Set Betweenness. Then, the following hold.

Ÿ Four relations T, , R, and are Asymmetric and Transitive (that is, strict partial orders), and they satisfy Strong Independence.⁵

Ÿ The weak temptation relation T and the weak resistance relation R are Strong Archimedean.⁶

We now consider geometric representations of the four strict partial orders. Define four cones corresponding to the four relations as follows.⁷

Ÿ A weak temptation cone is defined by.

Ÿ A strong temptation cone is defined by.

Ÿ A weak resistance cone is defined by.

Ÿ A strong resistance cone is defined by.

Temptation cones are defined as the set of “tempting directions”, and resistance cones are defined as the set of “resisting directions”. Corresponding to Lemma 1, those cones possess the following properties.

Lemma 2. Suppose that satisfies Preference, Continuity, Independence, and Set Betweenness.

Then, the following hold.

Ÿ Four cones, , , and are convex cones that represent their corresponding relations, respectively.⁸

Ÿ .

Ÿ The weak temptation cone and the weak resistance cone are faceless.⁹

4. A Geometric Proof for the Gul and Pesendorfer Theorem

In this section, we prove that any regular self-control preference relation admits a Gul and Pesendorfer representation.

If satisfies Axioms 1, 2, 3, and 4 and there are such that, we say that is a self-control preference relation. A self-control preference relation is regular if both and are nonempty.¹⁰

We first obtain two functions that represent temptation and self-control.

Lemma 3. There exist such that for any with,

Ÿ if and only if.

Ÿ if and only if.

Proof. We can prove this lemma in much the same way as in Abe ( [4] , Section 4), and hence omit the detail of proof here. A sketch of proof is provided in Appendix. In there, the proof goes as follows. We openly separate from and obtain v from their separating hyperplane. Similarly, we openly separate from and obtain w from their separating hyperplane.∎

We call function v a temptation utility and w a self-control utility.Suppose that.¹¹ Then, by Set Betweenness and Lemma 3, implies. With this fact, we can show the following.

Lemma 4. The self-control utility w must be written by for some constant and.

Proof. As stated above, when, implies. Hence, we find that and must imply. Then, we can apply Harsanyi’s [7] aggregation theorem and obtain some constant such that. Furthermore, we show below that and.

Because is a regular self-control preference relation, we can take such that and. From Lemma 3, we have, , , , , and. Let be such that and Then, since and, Lemma 3 and Set Betweeness imply and

Therefore, by the Harsanyi additive representation, we find. Then, by rearranging the representation and putting, we obtain the desired result. ∎

Lemma 4 means that the indifference curve of w lies between those of u and v when they pass a common point. From Lemma 4 together with Lemma 3, we further find the following fact that the self-control utility and the temptation utility exactly characterize temptation and costly self-control. The proof is immediate and thus omitted.

Lemma 5. and if and only if.

We now characterize U using w and v. The next lemma essentially characterizes the functional form of U.

Lemma 6. is cardinally equivalent to over.¹²

Proof. It immediately follows from Lemmas 1 and 5 that is a continuous affine function over. Then, from Continuity, must be a continuous affine function over.¹³

Let us now show that, for any, if and only if. Suppose but. Assume the existence of such that and.¹⁴ Consider translations for each. We assume that.¹⁵ Note then, under our supposition, that for all translations because v is a continuous affine function and hence satisfies Independence and Translation Invariance.¹⁶ On the other hand, for any close to 1 because and w is continuous. Hence, for any close to 1. Fix such a. We then have . Hence, from Set Betweenness,. However then, since is a continuous affine function over, implies, where the last equality follows from Lemma 3. This is a contradiction. Therefore, must imply. Similarly, we can prove the converse implication.

This lemma says that the ranking of and is determined by the temptation ranking of y and z when both y and z are more tempting than x but the individual can resist the temptations.¹⁷ Hence, we can plot indifference curves of on Δ as in Figure 1. This observation leads us to the desired form of representation.

Suppose. Take a z such that and. These lotteries are plotted in Figure 1. Then,. Recall from Lemma 4 that an appropriate scale-normalized commit-

ment utility is the difference between the self-control utility and a scale-normalized temptation utility:. Therefore, we can calibrate utility value of by the difference between the self-control utility of z and the normalized temptation utility of z. By the way of choosing z, we can hence calibrate utility

value of by the difference between the self-control utility of x and the normalized temptation utility of y, that is,. From Lemma 4, again, this means that utility value of is measured by the Gul and Pesendorfer form if we define and.

Formally, we prove the following.

Lemma 7. Define and by and. Let be the singleton restriction of. Then, is a representation of and a Gul and Pesendorfer model.

Proof. Since is cardinally equivalent to U, it is clearly a representation of. We now show that is a Gul and Pesendorfer model restricted on binary menus. Then, this lemma immediately follows from the extension result of Gul and Pesendorfer [3] .¹⁸ Assume that.¹⁹ Assume also that there is a z such that and.²⁰ Then, , , and . Moreover,

where the first equality follows from Lemma 6, the second from Lemma 3, and the third and the last from Lemma 4. This completes the proof.

Remark. Until now, we have focused on regular self-control preferences. Let us comment about the other cases. As heretofore, suppose that satisfies Axiom 1, 2, 3, and 4.

We first consider the case that implies or.This case is the degenerate case of no self-control preferences. Suppose that there exist such that and. We can observe such a situation in Figure 1 by rotating the indifference curve of around x in anticlockwise direction and placing it over the indifference curve of v. But, Figure 1 indicates that it is incompatible with Continuity. Hence, in this case, there is no case other than the two extreme cases: implies or implies. In both cases, Theorem 1 is trivial.

Let us then consider the case of self-control preferences but not regular. There are three cases: (i) and, (ii) and, and (iii) and.We note that the first two cases are impossible. To see why intuitively, consider case (i). In this case, there is no such that. This implies that if and only if. Self-control utility w must be cardinally equivalent to u. We can observe such a situation in Figure 1 by rotating the indifference curve of w around x in clockwise direction and placing it over the indifference curve of u. But, Figure 1 indicates that it is incompatible with Continuity.

Consider finally case (iii). In this case, implies. Hence, restricted on singletons is equal to R and the inverse of T. Therefore, commitment utility, self-control utility, and (−1) × temptation utility are cardinally equivalent. In this degenerate case, we can easily prove Theorem 1 by constructing v directly.^21,22

5. Discussion

We provided an alternative proof of the Gul and Pesendorfer’s utility representation theorem about temptation and self-control. In what follows, we clarify relations between our geometric approach and the Gul and Pesendorfer’s original approach.

Gul and Pesendorfer [3] proved the theorem in a way different from ours. Their approach is constructive. They directly define the temptation utility by for an arbitrarily fixed with and for sufficiently small. Observe from Continuity that. Combining this with the fact that , temptation utility v is viewed as measuring marginal utility for commitment. They showed under the conditions of Theorem 1 that v is indeed well-defined, continuous, and affine. This part serves as a building block to establish the desired representation.²³

The constructive approach and the geometric approach taken here bring us additional but different benefits beyond just establishing the representation theorem.²⁴ The former directly tells us how to calibrate temptation. On the other hand, the latter directly defines temptation and self-control in terms of preferences, so that it directly relates temptation and self-control utilities to particular intuitive properties of the underlying preferences.

The direct link between the two utilities and preferences promotes a better understanding of the Gul and Pesendorfer model. It highlights the reason why the self-control part can be written by sum of commitment utility and temptation utility. It is because we directly proved that all three dynamic considerations have linear structure and self-control considerations lie between commitment and temptation.

Moreover, the link provides the refined testable implications of the model. Our characterization of T, , R, and will be used to test the Gul and Pesendorfer model. First, it is helpful to design an experiment or a questionnaire. Since Independence and/or Set Betweenness are written in terms of choices over all menus, testing literally them entails a comprehensive examination of choices that uses not only small menus but large menus. The properties of T, , R, and provide simple testable implications of the model that are written by menus that include at most two elements.

Second, more importantly, because temptation utility v and self-control utility w are characterized by T, , R, and, the properties of those relations are testable predictions of a model with linear temptation utility and/or linear self-control utility. This means that if an individual’s choices do not obey the prediction of the Gul and Pesendorfer model, then the properties of T, , R, and may be useful in exploring the nature of observed violations and in considering a minimally extended model that accommodates the violations.²⁵

Acknowledgements

I would like to thank Fumio Dei, Hisao Hisamoto, Eiichi Miyagawa, and especially Hideo Suehiro, for their valuable comments and encouragement. I would also like to thank the anonymous reviewers for their many insightful comments and suggestions. Needless to say, the responsibility for any remaining errors rests with the author. This paper was supported by JSPS KAKENHI Grant Number 16K21038.

Cite this paper

Koji Abe, (2016) A Geometric Approach to Temptation and Self-Control. Theoretical Economics Letters,06,539-548. doi: 10.4236/tel.2016.63060

References

Appendix

Proof of Lemma 3 (Sketch). We first claim:

Claim 2.

Since, we have. We can show in the same way as the proof of Lemma 3 in [1] . Hence,. A similar argument proves.

Claim 3. There are two linear functional and on such that:

Ÿ for all and all.

Ÿ for all and all.

Note from Lemma 2 that (resp.,) is a faceless convex cone and misses convex set (resp.,). Putting it together with Claim 2, we can openly separate from over and from over . This proves Claim 3.

Define functions v and w on Δ by and for an arbitrarily fixed. By construction, those functions are affine. Furthermore, for any with, it holds that if and only if, and that if and only if. Finally, we claim:

Claim 4..

For, we let and. It then follows from the construction of v and that for all,. We can prove that v is continuous with the topology of weak convergence as in the supplement to the proof of Lemma 5 in [1] . In there, we used two properties of U: (1) U is upper semi-continuous and (2) implies. The latter property is guaranteed by the above fact that for all.

Similarly, using lower semi-continuity of U and the fact that for all, we can prove that w is continuous with the topology of weak convergence. ∎

Supplement to the proof of Lemma 6. As we showed in Section 4, is a continuous affine function over.

Let us show that, for any, implies. The converse implication is similarly proved.

Step 1. We show that there exist such that and.

By regularity, there are such that. This implies. If, then we have nothing to prove. Put and in that case. Suppose. Take such that. This implies. Since and, for any. Moreover, since v is continuous, there exists a unique such that. Put and. This completes the proof of Step 1.

Step 2. Take with and arbitrarily. Then, we show that for any, implies.

Suppose to the contrary that and. Let. Then, is a convex set with two or three dimension because and. Since is a finite dimensional convex set, we can take an algebraically interior point (see, Holmes [15] , p. 9). Hence, we can take a number such that, , , and are in a neighborhood of and is an algebraically relative interior point. Moreover, those lotteries satisfy, , and.

Consider now translations for. Note that there is a number such that in the neighborhood of for all, since is an algebraically relative interior point. Hence, belongs to Δ for all. We further show that for some. Since and v is a continuous affine function, for all. Since, we can take a such that. These two facts means for some.

Fix such a and consider the translation. Then,. By Set Betweenness,. However, since is a continuous affine function over,

,

where the last equality follows from Lemma 3. This is a contradiction.

Step 3. For any with, we show that implies.

By Step 1, there are such that and. Consider mixing, , , and.We can apply the result of Step 2 to these lotteries. ∎

Supplement to the proof of Lemma 7. We legitimate what we wrote in footnote 20. Observe first that there are such that and. This can be proved as shown in Step 1 in the supplement to the proof of Lemma 6, and we hence omit its proof. Suppose that. Let

, , and. Then, , , and. By Lemma 3, and. Since and, Lemma 4 implies. We consider three cases. Case 1:, Case 2:, and Case 3:. For Case 1, we set, , and. For Case 2, we take the such that and set, , and. For Case 3, we take the such that and set, , and. Then, , , and in all cases.

Then, by proof of Lemma 7, we have. From this, it follows that in all cases. We now demonstrate it for Case 3.Observe in this case that and . Substitute them into . Since U, u, and v are affine, we then immediately obtain. For the other cases, proofs are more direct since and in both cases.∎

NOTES

¹See Kreps [5] .

²Gul and Pesendorfer [3] consider an extended preference relation over lotteries of menus that is defined in an obvious way and show that Axioms 1 to 3 naturally induce the same properties to the extended relation. They then obtain a function U as a von Neumann and Morgenstern preference-scaling function for expected utility representation of that relation and show by construction that U is indeed a continuous affine function.

³Alternatively, we can rely on [6] to prove Lemma 0. Kopylov [6] applies the mixture space theorem to that is restricted on the set of all convex menus and directly obtains U as a von Neumann and Morgenstern expected utility of the restricted. He then uses the property that every menu is indifferent to its convex hull, which is indeed implied from Axioms 1 to 3, and extends U naturally over.

⁴The fact that these orders are strict partial orders is proved in Lemma 1 below.

⁵A binary relation R is said to be Asymmetric when implies, Transitive when and imply, and satisfies Strong Independence when if and only if.

⁶A binary relation R is Strong Archimedean if and imply that there is an such that.

⁷We need a linear space for defining those cones. Here, we take the linear space (over) as the set of all finite Borel signed measures over Z.

⁸Consider a binary relation R on a domain. Let.We say that C represents R when for some and in the domain of R imply.

⁹A face of a convex cone C is a nonempty convex subset F of C such that and for some imply. A convex cone C is said to be faceless if C is the only face of C.

¹⁰From Lemma 2, this is equivalent to the fact that there are such that and. This is consistent with the concept of regularity proposed in Gul and Pesendorfer [3] .

¹¹This commitment utility u is defined in Section 3.

¹²We can similarly show that is cardinally equivalent to w over.

¹³To see it, note that is continuous on. It is hence uniformly continuous. Define by for all. This is uniformly continuous and hence has a unique uniformly continuous extension over the closure of that domain (Kelly [8] , Theorem 26, p. 195]), where because and. Moreover, since is affine, so is its extension.

¹⁴Assuming the existence of such is without loss of generality. See Appendix for the detail.

¹⁵There is no loss of generality as for the footnote above. See Appendix for the detail.

¹⁶Function f on satisfies Translation Invariance if implies for any translation , or equivalently for any signed measure t such that and. As in [9] , any satisfies Translation Invariance.

¹⁷Similarly, the ranking of and is determined by the self-control ranking of y and z when x is more tempting than both y and z but the individual can resist the temptation.

¹⁸Suppose that u and v are continuous affine functions on Δ. Let U be a continuous function that represents some satisfying Set Betweenness and for all menus that have at most two elements. Then, that equation is valid for all menus.

¹⁹The other cases are straightforward.

²⁰In general, for arbitrarily fixed with, there may be no such z. However, in that case, we can construct another triple having the requested property by mixing x and y with other lotteries. Hence, we can apply the proof presented here to the constructed. We can then show that the shown result for is maintained for the original by the construction of. See Appendix for the detail.

²¹Take an arbitrarily. We can prove that is a continuous affine function over Δ as uin the first part of the proof of Lemma 6.Easy (but tedious) calculation then shows that, on binary menus, U is the Gul and Pesendorfer model with u and v, where for all.

²²We note that our geometric approach does not work well in this degenerate case. Specifically, in the proof of Lemma 7, we cannot take a z by which we calibrate utility value of.

²³Kopylov [6] proved Theorem 1 for a more general choice object than the one considered here and applied it to characterize various models associated with temptation. In his proof, he also constructs the temptation utility directly in the same spirit with Gul and Pesendorfer [3] by, where and are some convex menus such that. As Gul and Pesendorfer [3] did, he directly proved that can be written by the defined in the form of Theorem 1.

²⁴As Gul and Pesendorfer ( [3] , footnote 6) conjecture, there is another approach to prove Theorem 1 which is based on a representation theorem characterizing a general model called a finite additive expected utility representation. See Dekel, Lipman, and Rustichini [10] for the case of finite Z and Kopylov [11] for a more general choice object.

²⁵As in the literature of non-expected utility theories, identifying the nature of violations of a particular model (expected utility model in the literature) is an important issue in order to develop a new model that accommodates the violations. See MacCrimmon and Larsson [12] and Machina [13] . In the literature of temptation, Noor and Takeoka [14] extend the Gul and Pesendorfer model to admit an individual’s ability to exert self-control to depend on the faced menu. Providing a minimal generalization to the Gul and Pesendorfer model, they retain linearity of temptation utility. To this end, they characterize linear temptation utility in a way similar to ours.