Received 10 March 2015; accepted 21 April 2015; published 28 April 2015

ABSTRACT

We study the active retirement choice in a simple three-period life-cycle setting and demonstrate that time-inconsistent delayed retirement becomes a theoretical possibility. This helps to align theory with the intuition that delaying the date of retirement can be a reasonable response to spending too much and saving too little for retirement.

Keywords:

Quasi-Hyperbolic Discounting, Retirement, Life-Cycle Consumption and Saving

1. Introduction

Motivated by research findings in psychology and experimental economics, hyperbolic (or quasi-hyperbolic) discounting has become a conventional way to model and represent a divergence between earlier intentions and later choices^1,2. Some prominent economic topics that have been studied through the lens of hyperbolic discounting are delayed saving for retirement and the overaccumulation of debt. However, existing theoretical research about the effects of hyperbolic discounting on life-cycle saving behavior has largely ignored decision making with respect to labor supply margins of choice. Abstracting from labor supply margins, especially from the retirement decision, plausibly biases predicted savings outcomes since the decision of how much to save for retirement likely depends on when one intends to be retired, and when one intends to be retired likely depends on how much savings one plans to accumulate for retirement.

A few studies which do examine the consumption, saving, and retirement decisions in a three-period life- cycle setting are the studies by Diamond and Kőszegi [19] , Holmes [20] , and Findley and Feigenbaum [21] . The Diamond and Kőszegi [19] paper explores the conflict in retirement choice across the time-dated selves of a sophisticated individual with time-inconsistent preferences, while Holmes [20] and Findley and Feigenbaum [21] focus on time inconsistency in the retirement decision of a naive individual. A key feature of these studies is the assumption that the individual works during the first period and is retired in the third period, leaving an active retirement choice over the second period only. Findley and Feigenbaum [21] employ generalized assumptions about initial income and assets and document the possibility of time-inconsistent early retirement but also demonstrate that delayed retirement is impossible in this setting, meaning that the individual will never reverse his original, first-period intention to be retired during the second period by alternatively choosing to work when the second period arrives. The result that delayed retirement is impossible lines up with a finding in Holmes [20] and it stems from the fact that the individual has not yet had the opportunity to deviate from his original saving plan after only one period has elapsed. From the perspective of the first period, if the individual plans on retirement during the second period, then he will not feel the need to instead work during the second period once the second period has arrived since he still has the resources to follow through with his original plan to be retired in the second period.

³Findley and Caliendo [22] establish the possibility of delayed retirement in a high-frequency continuous-time setting using the hyperbolic discount function 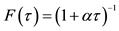with 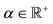for a delay of length.

Because intuition suggests that delaying retirement can be a logical response to saving insufficiently for retirement, the finding by Holmes [20] and Findley and Feigenbaum [21] that delayed retirement is impossible in this three-period setting has left a modest need to determine what assumptions can be made about the timing of the retirement period so that time-inconsistent delayed retirement is able to be represented using this three-pe- riod life-cycle model³. In this paper, we demonstrate how to modify the above setting so that time-inconsistent delayed retirement is a theoretical possibility. If the individual has choice over retirement during the last of the three periods, then he can initially intend to be retired during the third period from the perspective of the first period, but then reverse his original intention by actually working during the third period and never retiring. The reason that time-inconsistent delayed retirement is possible in this setting is due to the fact that the individual can choose at the start of the second period to deviate from his original plan about how much to save and consume during the second period. Reversing the original retirement intention, thereby choosing to work during the last period instead of being retired, sets up the individual to consume more during the second period than originally planned from the perspective of the first period. The possibility of time-inconsistent delayed retirement in a three-period life-cycle setting helps to align theory with the idea that delaying retirement is a reasonable response to saving too little for retirement.

2. Model

An individual lives for three periods and derives utility from consumption, , and from leisure, , in periods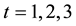. Period utility from consumption is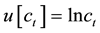. We modify the three-period setting in Findley and Feigenbaum [21] , which was itself a generalization of Diamond and Kőszegi [19] and Holmes [20] , such that full-time work in periods 1 and 2 is now exogenously imposed, so and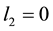. The individual has a discrete choice over leisure in period 3, specifically where is the utility of not working in period 3. From the perspective of the first period, the intertemporal utility function is

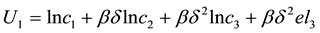, (1)

where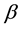, 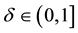are the short-term and long-term discount factors, respectively. From the perspective of the second period, the intertemporal utility function is

. (2)

If, then decision making can be dynamically inconsistent (Angeletos, Laibson, Repetto, Tobacman, and Weinberg [23] ). Like Holmes [20] and Findley and Feigenbaum [21] , we assume the individual is naive about the fact that his preferences are time-inconsistent⁴. This means that in period 1 the individual selects an allocation of consumption and leisure that he believes will be followed in the current and in future periods such that (1) is maximized. In period 2, the individual updates his choice allocations to maximize (2).

⁴Diamond and Kőszegi [19] investigate and focus on the conflict in retirement choice across the time-dated selves of a sophisticated individual with time-inconsistent preferences.

⁵could be the result of a bequest and/or borrowing or saving in previous periods (which is not modeled).

The individual earns income in periods. If the individual chooses to work in period 3, then unit income is earned. Therefore, the individual makes choices at period 1 with cash on hand, , where is the initial condition on the asset account balance⁵. Budget constraints are

, (3)

, (4)

, (5)

where and are savings from periods 1 and 2, respectively. We do not impose any restriction on in periods. Following previous studies we assume a zero interest rate to simplify the presentation, but this is an innocuous assumption regarding the existence of delayed retirement.

2.1. Optimization in Period 1

With the superscript on the choice variables denoting the period of planning, the individual intends to consume according to

, (6)

, (7)

, (8)

given the individual’s period-1 intention of his period-3 leisure choice,. Note that (6) also denotes the actual period-1 consumption allocation. These intentions imply period-1 savings,

. (9)

The individual will choose in period 1 an intention of his period-3 leisure, , in order to maximize his utility from the perspective of period 1. Therefore, he will plan to be retired during period 3 if

, (10)

where and is the threshold level of resources needed so that the individual can plan on being retired during period 3. Otherwise, the individual will plan to work during period 3.

2.2. Optimization in Period 2

Given, which depends on whether the individual intended to work or to be retired during period 3 from the perspective of period 1, the individual will select the consumption allocations from the perspective of period 2

, (11)

. (12)

It is important to note that (11) and (12) respectively specify the actual period-2 and period-3 consumption allocations since no time inconsistency remains at this point. Note also that these allocations are both dependent on the individual’s choice to actually work or to be retired during period 3, meaning that the individual will choose to maximize his intertemporal utility from the perspective of period 2. Therefore, the individual will choose to actually be retired during period 3 if

, (13)

where is the threshold level of savings that is needed to enable actual retirement during period 3. Otherwise, the individual will choose to work during period 3.

2.3. Time-Inconsistent Delayed Retirement

We examine whether or not the possibility can exist for the individual to initially intend to be retired during period 3 from the perspective of period 1, and then reverse his original intention by actually working during period 3. The retirement intention will occur if, but the individual will actually end up working during period 3 if. The latter of these two inequalities is equivalent to

, (14)

where is the threshold resource requirement needed to enable actual retirement during period 3, conditional on the fact that the individual initially planned on being retired during period 3.

From (10) and (14),

, (15)

meaning that there exists such that this sequence of time-inconsistent retirement timing is possible under the standard assumption of. In sum, if then the individual will plan to work during period 3. Yet if falls on the interval, which is nonempty given (15), then the individual will plan on being retired during period 3 from the perspective of period 1, but then the individual actually ends up working during period 3. And lastly, if then the individual will plan on being retired during period 3 from the perspective of period 1, and then the individual actually follows through by choosing retirement during period 3.

A simple numerical example helps to illustrate the point that time-inconsistent delayed retirement easily exists for a variety of assumptions, including larger values of e. If e = 1.62, β = 0.7, δ = 0.9, then. Note that income earned during period 3 is normalized to unity. Therefore, if, , and, then the above condition is satisfied given that.

It is of interest to see how the consumption allocations are altered when the individual is time-inconsistent in his retirement timing. Given (7), the individual selects

, (16)

if he intends to be retired during period 3 from the perspective of period 1. With reflecting the period-1 intention to be retired during period 3, the individual then selects in period 2

(17)

It is clear to see in (17) that the individual will end up consuming more in period 2 than originally planned from the perspective of period 1. This is independent of whether or not the individual actually follows through with being retired during period 3. Yet, if the individual abandons the original plan by deciding to actually work during period 3, then this will have the effect of increasing consumption in period 2 even more.

Consumption in period 3 will be

. (18)

If the individual sticks to his plan to be retired in period 3, then time inconsistency in the saving decision will cause the individual to consume less in period 3 than he had originally intended from the perspective of period 1, given that the coefficient on in (18) is less than one. However, if the individual changes his mind and does not retire, then the addition of the second term in (18), which is positive, may overcome the fall in consumption due to the time inconsistency. Thus, it is a quantitative question whether consumption during period 3 will be higher or lower than what was originally planned. We find that consumption in period 3 will be lower than what was originally planned only under extreme (yet still plausible) parameterizations. Indeed, it is the case that period-3 consumption is higher with work during period 3 relative to what would be consumed when retirement during period 3 was originally intended. More precisely, if and only if the following condition holds,

, (19)

which is predicated on the presence of time inconsistency in the retirement decision. Using the example above with the parameter values of, , and, then time-inconsistent delayed retirement results in the model if is greater than yet less than. Parameter values of, , and imply, which satisfies the range for time-inconsistent delayed retirement to occur. The values of and imply, and the values of and imply, therefore satisfying (19) such that. Indeed, the following consumption allocations result from this parameterization:, , , , and. In order for period-3 consumption to be lower when working during period 3, relative to what would be consumed if retirement during period 3 was originally intended, extreme present bias would need to exist or extremely large levels of resources would need to be available to the individual (remembering that the unobservable parameter would need to be adjusted appropriately so that time-inconsistent delayed retirement exists).

In sum, the individual may choose in period 2 to forego retirement during period 3 so as to increase his consumption during period 2 even more than originally planned. Moreover, it is often the case that foregoing retirement has the effect of increasing consumption during period 3 as well, compared to what was originally planned. Of course, increases in utility from unequivocally higher consumption in period 2 and possibly higher consumption in period 3 come at the sacrifice of forgone leisure utility in period 3 that would otherwise be enjoyed.

3. Summary

Evidence indicates that people often save insufficiently for retirement due to a present bias in consumption. Common intuition and observation suggest that delaying the date of retirement can be a logical way for an individual to cope with having saved too little. Yet there exists a disconnect between this common intuition and existing economic theory, given that recent research documents that time-inconsistent delayed retirement is theoretically impossible in a particular three-period life-cycle setting. In this paper, we demonstrate how to modify that setting such that time-inconsistent delayed retirement is possible theoretically. This helps to align theory with the idea that delaying retirement can be a reasonable response to spending too much and saving too little for retirement.

We conclude by mentioning an interesting related topic to study in this literature: examining a life-cycle model in which an individual chooses the intensity of labor-leisure in each period, in addition to selecting the age at which to retire. A failure by an individual to follow through with plans about how intensely to work each period could be an additional reason (aside from spending too much and saving too little) to delay the date of retirement. Yet, we acknowledge that it might be possible for the presence of time-inconsistent decision making along the intensive margin to somehow counteract the need to delay retirement. We believe that examining these possibilities deserves more attention, and we have therefore placed this topic on the agenda for future research.

Acknowledgements

We acknowledge and thank an anonymous reviewer for helpful suggestions.

References

NOTES

¹Research in psychology and experimental economics typically finds evidence of hyperbolic discounting (e.g., Rachlin, Raineri, and Cross [1] ; Kirby and Maraković [2] ; Cairns and van der Pol [3] ; Frederick, Loewenstein, and O’Donoghue [4] ; Ainslie [5] ). Yet, some studies find very little empirical support for hyperbolic discounting (e.g., Harrison and Lau [6] ; Andreoni and Sprenger [7] ; Dohmen, Falk, Huffman, and Sunde [8] ; Sutter, Kocher, Glätzle-Rüetzler, and Trautmann [9] ).

²A divergence between intentions and actual behavior requires that individuals naively fail to account for their own time inconsistency (O’Donoghue and Rabin [10] -[13] ; Caillaud and Jullien [14] ; Prelec [15] ; Beshears, Choi, Laibson, and Madrian [16] ; D’Orlando and Sanfilippo [17] ; Herweg and Müller [18] ).