ABSTRACT

This paper studies the impact of relative performance on portfolio choices and asset prices when fund managers differ in size and exogenous financial shocks. We find that with these heterogeneities, fund managers change their trading behaviors significantly.

1. Introduction

In the fund management industry, money managers care about their relative standings among the peer group. A common explanation for this is that money managers have incentives to increase their compensation and hence their assets under management given a positive and convex relationship between cash flows into the fund and relative performance¹. The concerns about relative performance could distort the trading behavior of agents in the market, hence having asset pricing implications.

When studying the impact of relative performance on portfolio choices or asset prices, one needs to consider a setting with heterogeneous agents. If agents are exactly identical, relative performance would not play any role as agents perform equally. Therefore, in order to study relative performance, agents need to be different in some ways. In related literature, existing papers focus mainly on one dimension of heterogeneity at a time. For example, Basak and Makarov [4] and Kapur and Timmerman [5]² consider money managers with different risk aversions. In fact, funds might differ in other dimensions as well such as size, profitability or target customer groups. For example, Chen, Glodstein and Jiang [8] find that funds with different customer groups (retail versus institutional investors) have different outflow patterns. With those possible heterogeneities, how do fund managers change their trading behaviors when relative performance is a concern? This paper aims to contribute to our understanding of this question.

In this paper, we focus on two dimensions of heterogeneities among two fund managers, namely, exogenous financial shocks and relative size (profitability). The major findings of this study are twofold: 1) The combination of different size and relative performance results in a lower risky asset price; 2) The effect of different exogenous financial shocks and relative performance on asset price depends on how the exogenous financial shock outside the market covaries with the asset payoff. To our best knowledge, this is the first paper that considers the interaction between relative performance, different exogenous financial shocks and relative size.

In our framework, relative performance is defined as the difference between individual and average return. Difference in size implies different trade-offs between risk and return. A manager with higher size (lower profitability) tends to submit a higher demand to achieve a decent return, whereas a manager with lower size (higher profitability) tends to submit a lower demand to reduce the risk. In equilibrium the aggregate demand is lower, resulting in a lower price.

The exogenous shocks to the cash flows of each fund can be interpreted as exogenous labor income, exogenous wealth, or the impact of different customer groups. We show that the optimal demand of each agent changes with respect to the relative benefit of the risky asset as a natural hedge of shocks to both funds³. Intuitively, one would increase her demand for the risky asset if the covariance between the asset payoff and the exogenous shock is lower, but the other manager would also have incentives to increase her demand due to relative performance concerns. Moreover, differences in size can also change the effect above in equilibrium. Overall, we derive interesting results on the interaction between relative performance, size and exogenous financial shocks and its implications on asset prices.

The rest of the paper is organized as follows. Section 2 presents the model. Section 3 derives and analyzes the equilibrium conditions. Section 4 concludes.

2. The Model

Our model has two dates, 0 and 1. In the market, there are two assets: one is risky and the other is risk-free. For simplicity, we assume the risk-free rate is zero. The risky asset has a final payoff d and a positive net supply S. Two fund managers are assumed to have the CARA utility function over their final consumption at time 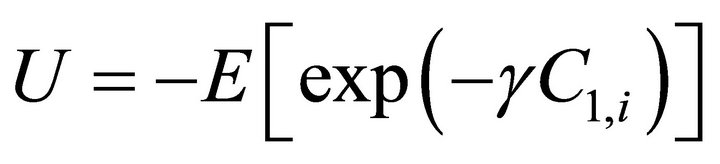1.

(1)

Throughout the paper, an index 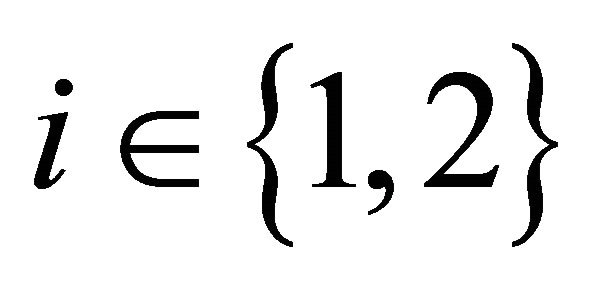is used to indicate manager’s type. Each manager receives some endowment 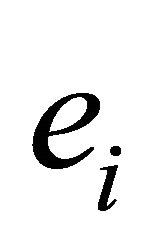at time 1 which is not tradable in the market4. These random variables are exogenous and assumed to follow normal distribution⁵. Specifically,

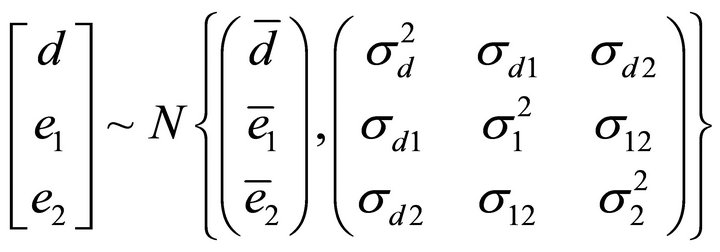
In addition, we assume that two funds have different initial size. Let the fund size of manager 1 be W and that of manager 2 be λW at t = 0 with λ > 0. The compensation contracts for manager 1 and manager 2 are

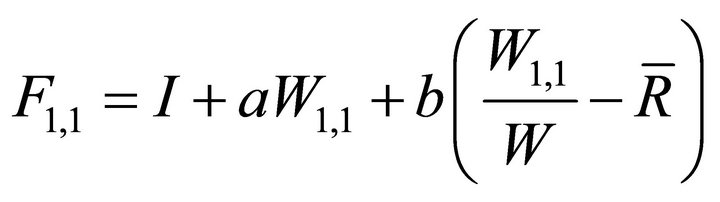(2)

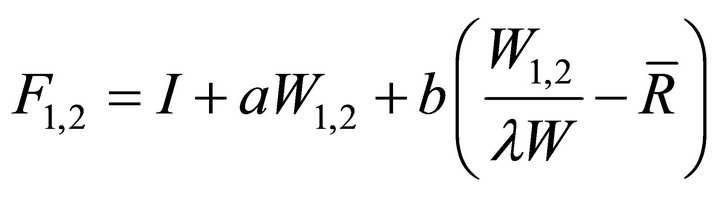(3)

where I⁶ is just some positive constant, and 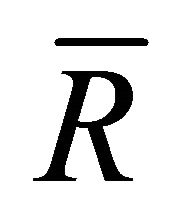is the average return of the industry defined as

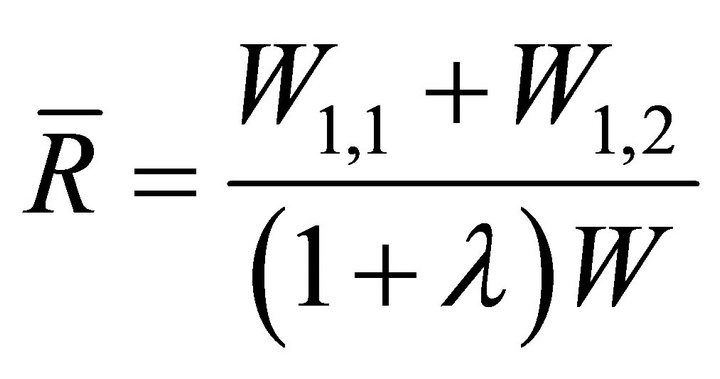(4)

We can think of 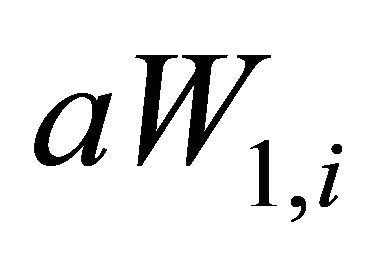as the management fee as a fixed proportion of assets under management which is quite common in the industry, and 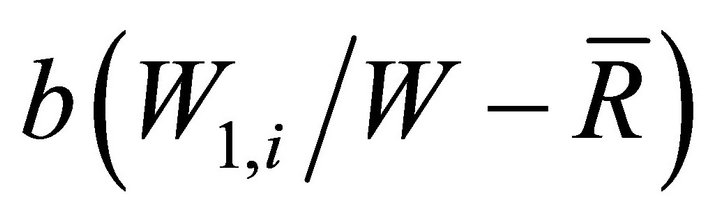as the relative performance part of the contract which can be thought of as fund flows⁷.

Given the compensation, the final consumptions of managers are given by

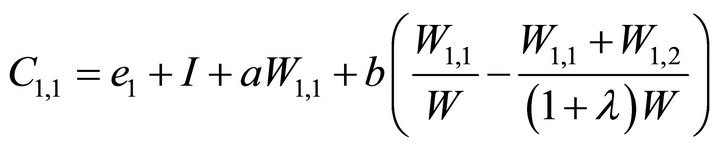(5)

(6)

Together with the expected utility function, we can solve the equilibrium in closed form.

3. Portfolio Choices with Relative Performance

Given the normal distribution and CARA utility function, the optimization problem can be simplified as a meanvariance one. In particular, it is given by

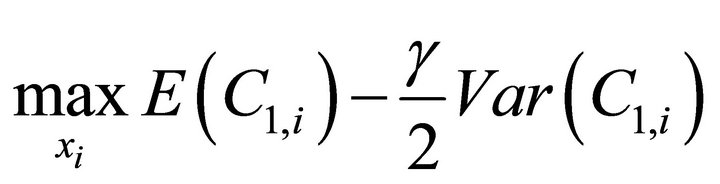(7)

We obtain the optimal demands by solving the FOCs:

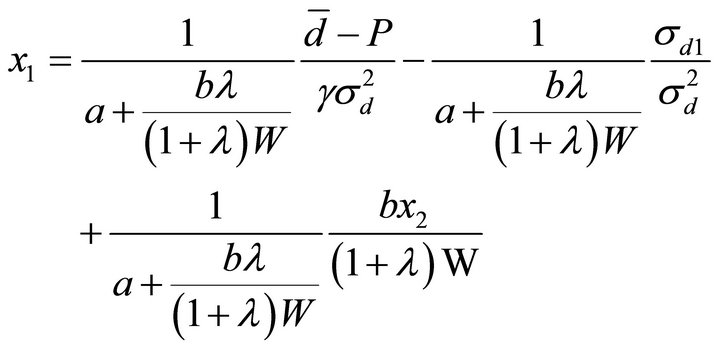(8)

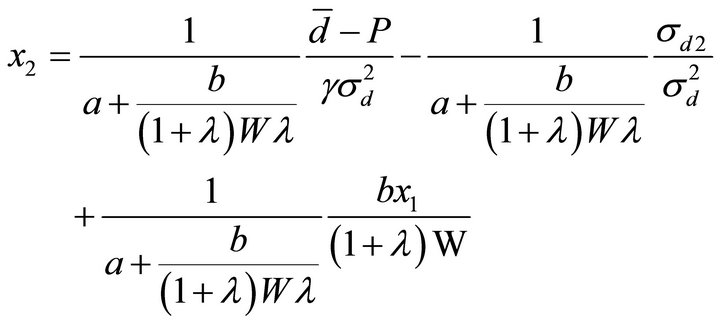(9)

We can see that 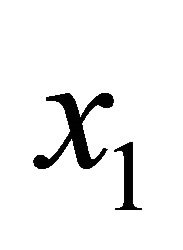is a function of, and vice versa. This means that two agents adjust their optimal demands based on the demands of the counterpart, reflecting their concerns about relative performance.

4. Analysis

Given two equations, we have two unknowns which can be solved as follows:

The optimal demands in the proposition can be decomposed into three parts. The first part is the demand without relative performance. It consists of the myopic demand which captures the nature of CARA utility function with normal-distributed payoffs, and the hedging demand which hedges the exogenous shock. The hedging demand depends on the covariance between the risky asset payoff and the exogenous shock. Agents will buy more risky asset when the shock and the payoff are negatively correlated because the asset works as a natural hedge against the shock. If we set b = 0 (no relative performance in the contract), we can see that this first part will be the only term in the agents’ demands.

The second part measures the effect of the relative performance and size on demand. Let us ignore the third part for a moment. When λ > 1, the second part is negative for manager 1 and positive for manager 2, implying that manager 2 will trade more aggressively than the manager 1. When λ < 1, the opposite is true. However, note that the second part is not monotonic in λ: When λ goes to infinity, the relative performance effect for manager 1 disappears, and manager 2 does not trade at all; the opposite is true when λ goes to 0.

The parameter of relative size (λ) captures the profitability of two managers. When λ > 1, manager 2 will achieve a lower return than manager 1, given that they both hold the same amount of risky asset. Given the incentive to improve relative performance in (3), manager 2 will tend to trade more aggressively. For manager 1, aggressive trading by manager 2 increases the variance of her compensation given relative performance, and hence she will tend to trade less aggressively given (2). This effect is not monotonic in λ because when λ becomes large, the market share of manager 1 becomes negligible (hence manager 2’s concern about relative performance disappears), but manager1’s compensation still depends on the performance of manager 2 and manager 1 needs to hedge that risk (hence manager 1 does not trade all all). When λ < 1, manager 1 will have lower profitability, and the same story holds. Note that when λ = 1, the effect of relative performance on size disappears.

The third part is related to 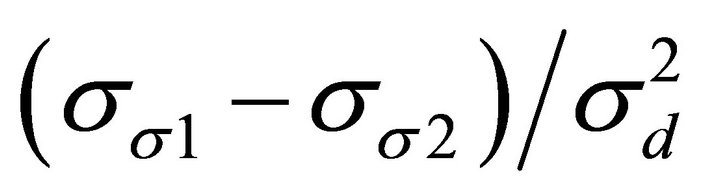which is the effect of relative performance and exogenous shocks. When the two fund managers have different exogenous shocks, the hedging benefits of the risky asset are different. For manager 1, when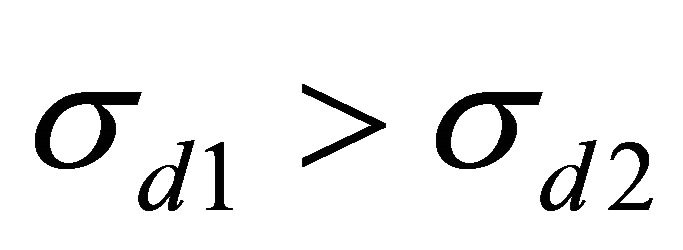, the benefit of the asset as a natural hedge for manager 1 is lower than that for manager 2. When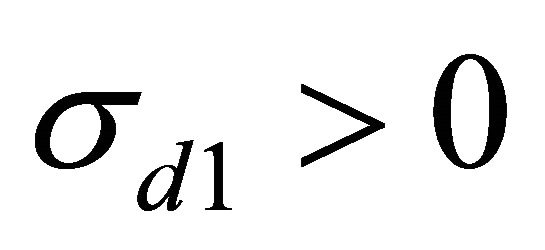, the optimal action for manager 1 is to decrease her total demand to hedge the exogenous shock. However, she knows that manager 2 will decrease less, or even increase the demand. This would result in lower relative performance for manager 1, who would in turn have incentives to increase the demand. The case for is similar.

The equilibrium price is given in the following proposition:

Proposition 1. By market clearing, we have

The above proposition gives us the equilibrium price. In addition to the price without relative performance, we have two more terms. The first one is the effect of relative performance and size and the second one is the effect of relative performance and exogenous shocks.

When λ is not equal to one, the second term is negative, implying that the effect of relative performance and size leads to a lower risky asset price. Although the manager with a higher market share will tend to trade more aggressively, the manager with a lower market share reduces her demand to a greater extent. As a result, the price is lower in the absence of exogenous shocks.

Now let’s look at the third term. Suppose first λ = 1. Then the price becomes

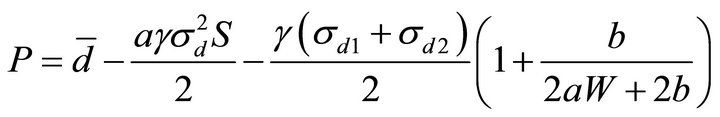
We can see that the third term is smaller if 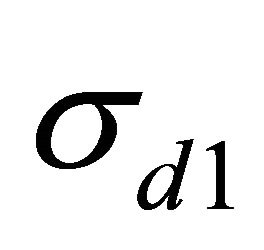or 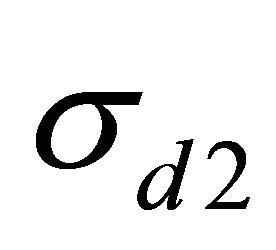increases. Intuitively, fund managers will reduce their demand for the risky asset if the covariation between the payoff and the exogenous shock is positive, resulting in a lower asset price. Moreover, this effect is greater when b increases, i.e. fund managers have greater incentives to hedge against the exogenous shocks with relative performance.

Now suppose λ > 1. This will result in a lower price if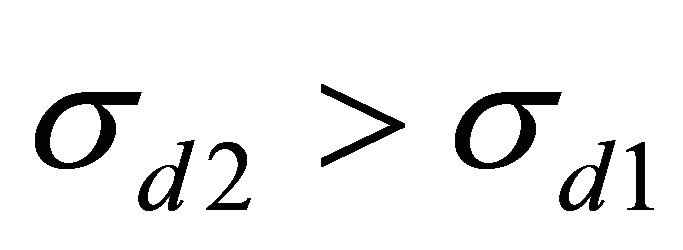, and vice versa. The intuition is that when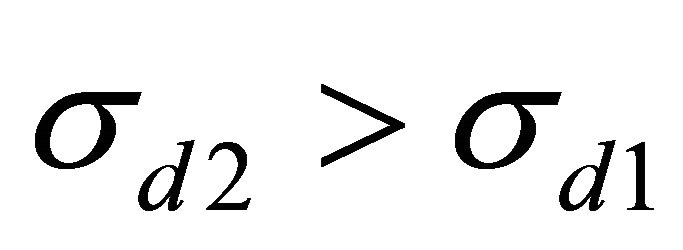, manager 1 will have greater incentives to hedge and a greater demand, and manager 2 will have incentives to increase her demand as well due to relative performance concerns; but the increase in manager 2’s demand is lower if manager 1’s market share is lower (λ > 1), resulting in a lower price. A similar story holds for λ < 1.

5. Conclusion

In the paper, we consider the effect of relative performance on portfolio choices and asset prices when fund managers have different size and exogenous financial shocks. We find that the effect of relative performance and size effectively changes the risk aversion of fund managers. That is, they increase or decrease the demand without relative performance. However, in general, the relative performance and size lead to a lower aggregate demand, hence a lower stock price. The effect of relative performance and exogenous shock works as a hedging demand of each fund manager. How fund managers hedge depends on the relative hedging benefit of the asset to the exogenous shock.

REFERENCES

NOTES

^*Corresponding author.

¹Empirical evidence can be found in Chevalier and Ellison [1], Sirri and Tufano [2] and Huang, Wei and Yan [3].

²Those papers, same as ours, consider the performance relative to the peer group. However, some other papers, for example, Basak and Pavlova [6], Kaniel and Cuoco [7], consider the performance relative to some passive index benchmark. In our paper, the relative performance is endogenous, which is more general than passive benchmark.

³It is measured by the covariance between the asset payoff and each shock.

⁴We can think of the endowments as coming from different types of investors (customer groups) who may withdraw or invest money based on their financial needs. Investors may invest or withdraw due to behavioral or fundamental reasons. For example, retail investors may be more vulnerable to shocks to the economy and tend to withdraw more during the downturn.

⁵This can also be justified for modeling choice.

⁶It is included to be consistent with some other standard contract in the industry.

⁷When the return of fund 1, 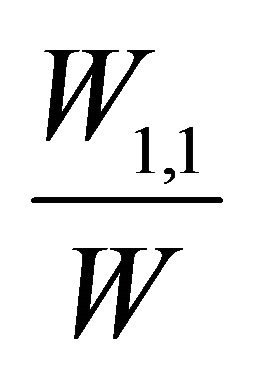, is greater than that of fund 2, 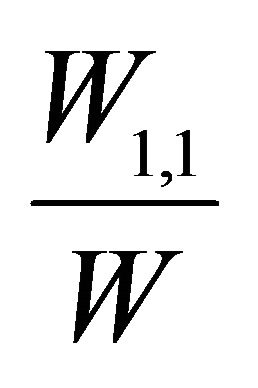, there will be cash flows into fund 1, increasing manager 1’s compensation, and vice versa.