Technology and Investment
Vol.1 No.4(2010), Article ID:3209,4 pages DOI:10.4236/ti.2010.14029
A Comparison of Stock Market Efficiency of the BRIC Countries
1Department of Economics, The Chinese University of Hong Kong, Hong Kong, China
2Department of Finance, The Chinese University of Hong Kong, Hong Kong, China
E-mail: chong2064@cuhk.edu.hk
Received June 14, 2010; revised October 11, 2010; accepted October 16, 2010
Keywords: Simple Moving Average, Relative Strength Index, Moving Average Convergence Divergence, Momentum
Abstract
This article compares the stock market efficiency of Brazil, Russia, India and China (commonly referred to as BRIC). The profitability of trading rules associated with the Simple Moving Average (SMA), the Relative Strength Index (RSI), the Moving Average Convergence Divergence (MACD) and the Momentum (MOM) are evaluated. It is found that these indicators are most profitable in the Russian stock market. The Brazilian stock market is found to be the most efficient market among the BRIC. An explanation for such a discrepancy is provided.
1. Introduction
Over the past two decades, a good number of empirical studies have been conducted to evaluate the performance of different trading rules. Earlier studies focus on the appealing Variable-length Moving Average (VMA) rule, which states that a long position should be taken if the short-term VMA is above the long-term VMA, and vice versa. The VMA rule has been proven profitable in many studies. For example, Brock et al. [1] show that the VMA trading rule generates excess returns in the US market. Hudson et al. [2] and Mills [3] also find that the rule is profitable in the FT30 index1. These early studies, however, focus on developed markets. Over the past decade, there is an increasing number of studies on the performance of technical trading rules in emerging markets. One strand of literature examines the currency market. For example, Martin [7] applies the moving-average rule to 12 emerging currencies and shows that the risk-adjusted return is not significant. Lee et al. [8] demonstrate that the moving average rule and the channel rule are profitable for the Brazilian Real, the Mexican Peso, and the Venezuelan Bolivar. Ahmed et al. [9] find that the moving average rule can beat the buy-and-hold strategy in the daily spot exchange rates of Chile, Mexico, Indonesia, the Philippines, South Korea, and Thailand. Craig et al. [10] show that including emerging market currencies in an investment portfolio substantially increases the Sharpe ratio associated with carry trades. Chong and Ip [11] demonstrate that the momentum rule is profitable in emerging currency markets.
Another strand of literature focuses on emerging stock markets. For example, Ito [12] finds profitable technical rules in the stock markets of Indonesia, Mexico and Taiwan. Parisi and Vasquez [13] show that buy signals generate higher returns than sell signals in the Chilean stock market. Hameed and Ting [14] find evidence of predictability for the Malaysian stock market. Gunasekarage and Power [15] conclude that technical trading rules have predictive power in the markets of Bombay, Colombo, Dhaka and Karachi. Kang et al. [16] find significant returns of momentum strategies in the Chinese A-share market2.
Recently, there has been an increasing interest in the study of BRIC3, which refers to Brazil, Russia, India and China, the four largest and fast growing emerging countries. Given their increasingly important roles in the world financial markets, this paper attempts to compare the efficiency of the BRIC stock markets. The profitability of four popular technical indicators, namely, the Simple Moving Average (SMA), the Relative Strength Index (RSI), the Moving Average Convergence Divergence (MACD) and the Momentum (MOM), are reported. It is found that the trading rules associated with these indicators outperform the buy-and-hold strategy in India and Russia, while the stock market of Brazil is shown to be relatively efficient. Our results also show that, in general, the 10-day SMA and MACD rules are most profitable, followed by the 14-day RSI, 10-day SMA and 40-day MOM, while the 250-day SMA is the least profitable. The remainder of the paper is structured as follows: Section 2 describes the data and methodology used. Section 3 reports the results and Section 4 concludes the paper.
2. Data and Methodology
Our data are sourced from DataStream International available at the University Library of the Chinese University of Hong Kong. The data set consists of the daily closing indices of the stock markets of Brazil, Russia, India and China from September 1995 to November 2008. The details are shown in Table 1.
Let SMAN(t) be the N-day simple moving average and P(t) be the closing value of the stock market index at day t. When the index crosses its moving average from below, the market is considered bullish, while it is considered bearish otherwise. Therefore, we define the SMA trading rule at time t as Buy if P(t − 1) < SMA(t − 1) and P(t) > SMA(t);
Sell if P(t − 1) > SMA(t − 1) and P(t) < SMA(t).
The 10, 50 and 250-day SMA are examined.
The RSI index was developed by Wilder [20]. An N-day RSI is the ratio of the sum of all positive changes of prices to the sum of absolute changes of prices in N days, multiplied by 100:
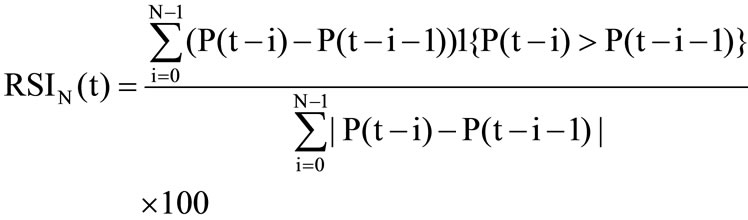
where |P(t − i) − P(t − i − 1)| is the absolute daily change of the index, and 1{P(t − i) > P(t − i − 1)} is an indicator function which equals one if P(t − i) > P(t − i − 1), and equals zero otherwise. The RSI ranges from 0 to 100. If the index is trending down, the RSI will approach zero. If the index is trending up, the RSI will approach 100. The middle of this range is often regarded as the cut-off point of bullish and bearish markets. The RSI trading rule at time t is defined as follows:
Buy if RSI(t − 1) < 50 and RSI(t) > 50;
Sell if RSI(t − 1) > 50 and RSI(t) < 50.
The rule states that a buy signal is triggered when the RSI crosses 50 from below, while a sell signal is generated when it crosses 50 from above. In this paper, the commonly used 9-day and 14-day RSI will be examined.
The moving average convergence divergence (MACD) proposed by Appel [21] is the difference between the long-term exponential moving average (EMA) and the short-term EMA. The N-day exponential moving average at time t is defined as EMAN(t) = aP(t) + (1 − a)EMAN(t − 1)EMAN(1) = P(1)a = 2/N.
where P(t) is the index value at time t. The initial EMA is defined as the closing value of the index at time 1. For any integer M > N > 0, the MACD is defined as MACD(t) = EMAM(t) − EMAN(t).
In addition, we define the signal line as the EMA of the MACD. The MACD rule is then defined as follows:
Buy if MACD(t − 1) < signal-line(t − 1) and MACD(t) > signal-line(t);
Sell if MACD(t − 1) > signal-line(t − 1) and MACD(t) < signal-line(t).
Thus, a buy signal is generated when the MACD crosses its signal line from below, while a sell signal is generated otherwise. Following Murphy [22], we use the 12 and 26-day EMAs as our short and long-run EMAs, and the 9 and 14-day EMA of the MACD as our signal lines.
The momentum indicator (Chande and Kroll [23]) is defined as the difference between the closing prices of two trading days. Specifically, the N-day momentum is constructed by subtracting the closing price at time t – N from the closing price at time t.

Table 1. The stock market indices of BRIC and their sample periods.
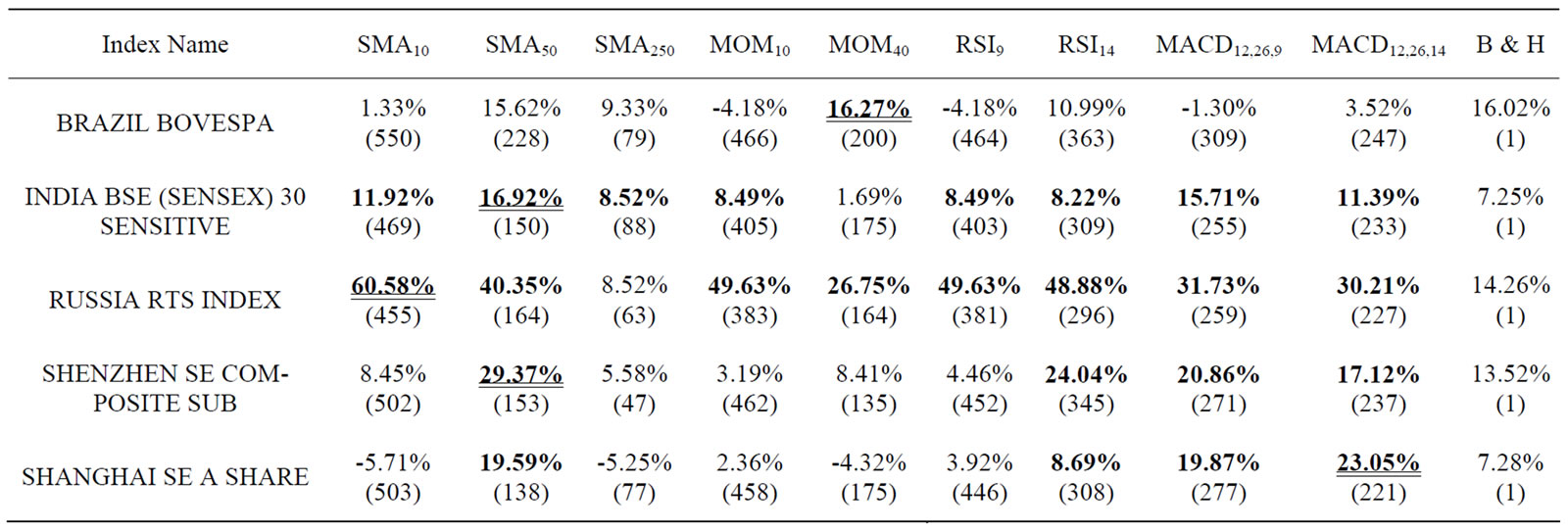
Table 2. The annual rate of return.
MOMN(t) = P(t) − P(t − N).
The MOM trading rule is defined as follows:
Buy if MOM(t − 1) < 0 and MOM(t) > 0;
Sell if MOM(t − 1) > 0 and MOM(t) < 0.
Thus, a buy signal is triggered when the MOM crosses the zero line from below, while a sell signal is triggered when the MOM crosses the zero line from above. In this paper, we examine the performance of the 10-day and 40-day momentum indicators.
Short-selling is allowed in our analysis, while consecutive buys or sells are not. Thus, a position will not be reversed until the arrival of an opposite signal. To compare the returns across countries, we evaluate the performance of these trading rules using the annualized rate of return. Since there are around 250 trading days per year, we define Annual Rate of Return
= (1 + r1) (1 + r2) … (1 + rm)250/T – 1where 1 + rj = S(j)/B(j);
S(j) and B(j) are the selling and buying price of the index respectively in the jth transaction, m is the number of transactions and T is the number of trading days in our sample.
3. Results
Table 2 reports the annualized rate of return generated by the aforementioned trading rules. The figures in parentheses are the numbers of transactions for the corresponding index and trading rule. For each index, the annualized return of each trading rule is compared with the buy-and-hold benchmark. The bolded figures denote returns above the buy-and-hold benchmark, and the highest rate of return is underlined. If two trading rules generate the same return, we prefer the rule with the least number of transactions. The highest return for each market ranges from 16.23% (Brazil) to 60.58% (Russia). Amongst these nine trading rules, the SMA10, SMA50 and the two MACD rules are most profitable. The rules of RSI14 and MACD yield excess returns in at least four markets, whereas the rule of SMA250 is the least profitable. Among these trading rules, the SMA250 rule for the case of Russia and the MOM40 rule for the case of India cannot generate excess returns.
Our trading rules beat the buy-and-hold strategy in the India BSE (Sensex) 30 Sensitive and the Russia RTS Index. The trading-rule profits are attributable to the serial correlation in stock returns. In general, this serial correlation is higher for emerging markets than for developed markets (Harvey [24]). Note that the Brazilian market is quite efficient. Most trading rules cannot beat the buy-and-hold benchmark, except for the MOM40 rule. Our trading rules slightly beat the buy-and-hold in the Indian market. For the case of Russia, the SMA10 rule generates the highest return. An annualized return of 30% can be achieved for all rules other than the SMA250 rule. The results for China are mixed. The SMA50, RSI14 and MACD rules beat the buy-and-hold strategy, while other rules do not.
4. Conclusions
This paper examines the stock market efficiency of Brazil, Russia, India and China. The profitability of trading rules associated with the SMA, RSI, MACD and MOM are evaluated. Our results show discrepancies in trading-rule performance among the BRIC markets. A reason for this lies in the history of the stock exchanges of these countries. Note from Table 1 that the founded/reopening years of the stock exchanges of these markets vary. Our trading rules perform quite well in markets with a relatively short history (Russia), but do not work in markets with a long history (Brazil). This provides indirect evidence for the general observation that stock markets are getting more efficient over time (Li et al. [25]). A limitation of our study is that we do not consider transaction costs here. Transaction costs are generally higher in emerging markets as compared to the developed markets. The transaction cost mainly consists of the bid-ask spread and the stamp duty. For developed markets, the cost is about 0.1% to 0.5% for a round-trip transaction. For emerging markets, even the cost is two or three times higher, the overall annual cost will still be lower than 5% if there are ten transactions per years. Our results are robust to the presence of transaction costs. For example, for the RUSSIA RTS INDEX, the annualized returns of most trading rules are over 30%. As the number of transactions in a year is general less than 20, the annualized transaction cost in this market is about 10%. Even this 10% cost is taken into account; it is still profitable to apply our trading rules to the Russian market. A further development of our study would be to allow for transacttion costs, or to include more emerging markets from different continents, such as South Africa, United Arab Emirates, Hungary and Malaysia in our analysis.
5. References
[1] W. Brock, Lakonishok and B. LeBaron, “Simple Technical Trading Rules and the Stochastic Properties of Stock Return,” Journal of Finance, Vol. 47, No. 5, 1992, pp. 1731-1764.
[2] R. Hudson, M. Dempsey and K. Keasey, “A Note on the Weak Form Efficiency of Capital Markets: The Application of Simple Technical Trading Rules to UK Stock Prices–1935 to 1994,” Journal of Banking and Finance, Vol. 20, No. 6, 1996, pp. 1121-1132.
[3] T. C. Mills, “Technical Analysis and the London Stock Exchange: Testing Trading Rules Using the FT30,” International Journal of Financial Economics, Vol. 2, 1997, pp. 319-331.
[4] J. L. Treynor and R. Ferguson, “In Defense of Technical Analysis,” Journal of Finance, Vol. 3, 1985, pp. 757-773.
[5] K. Y. Kwon and R. J. Kish, “Technical Trading Strategies and Return Predictability: NYSE,” Applied Financial Economics, Vol. 12, No. 9, 2002, pp. 639-653.
[6] T. T. L. Chong and T. H. Lam, “Are Nonlinear Trading Rules Profitable in the U.S. Stock Market?” Quantitative Finance, Vol. 10, No. 9, 2010, pp. 1067-1076.
[7] A. D. Martin, “Technical Trading Rules in the Spot Foreign Exchange Markets of Developing Countries,” Journal of Multinational Financial Management, Vol. 11, 2001, pp. 59-68.
[8] C. I. Lee, J. C. Gleason and I. Mathur, “Trading Rule Profits in Latin American Currency Spot Rates,” International Review of Financial Analysis, Vol. 10, No. 2, 2001, pp. 135-156.
[9] P. Ahmed, K. Beck and E. Goldreyer, “Moving Average Technical Trading Strategies for Currencies of Emerging Economies,” Managerial Finance, Vol. 31, 2005, pp. 14-28.
[10] B. Craig, M. Eichenbaum and S. Rebelo, “The Returns to Currency Speculation in Emerging Markets,” American Economic Review, Vol. 97, No. 2, 2007, pp. 333-338.
[11] T. T. L. Chong and H. Ip, “Do Momentum-Based Strategies Work in Emerging Currency Markets?” Pacific-Basin Finance Journal, Vol. 17, 2009, pp. 479-493.
[12] A. Ito, “Profits on Technical Trading Rules and TimeVarying Expected Returns: Evidence from Pacific-Basin Equity Markets,” Pacific-Basin Finance Journal, Vol. 7, 1999, pp. 283-330.
[13] F. Parisi and A. Vasquez, “Simple Technical Trading Rules of Stock Returns: Evidence from 1987 to 1998 in Chile,” Emerging Markets Review, Vol. 1, 2000, pp. 152- 164.
[14] A. Hameed and S. Ting, “Trading Volume and Short Horizon Contrarian Profits: Evidence from the Malaysian Market,” Pacific-Basin Finance Journal, Vol. 8, 2000, pp. 67-84.
[15] A. Gunasekarage and D. M. Power, “The Profitability of Moving Average Trading Rules in South Asian Stock Markets,” Emerging Markets Review, Vol. 2, No. 1, 2001, pp. 17-33.
[16] J. Kang, M. H. Liu and S. X. Ni, “Contrarian and Momentum Strategies in the China Stock Market: 1993- 2000,” Pacific-Basin Finance Journal, Vol. 10, 2002, pp. 243-265.
[17] M. Ratner and R. P. C. Leal, “Tests of Technical Trading Strategies in the Emerging Equity Markets of Latin America and Asia,” Journal of Banking and Finance, Vol. 23, 1999, pp. 1887-1905.
[18] E. J. Chang, E. J. A. Lima and B. M. Tabak, “Testing for Predictability in Emerging Equity Markets,” Emerging Markets Review, Vol. 5, No. 3, September 2004, pp. 295-316.
[19] J. O’Neill, “Building Better Global Economic BRICs,” Goldman Sachs Economic Research Paper 66, 2001.
[20] J. W. Wilder, Jr., “New Concepts in Technical Trading Systems,” Trend Research, 1978.
[21] G. Appel, “The Moving Average Convergence Divergence Method,” Great Neck, Signalert, 1979.
[22] J. J. Murphy, “Technical Analysis of the Financial Markets,” New York Institute of Finance, New York, 1999.
[23] T. Chande and S. Kroll, “The New Technical Trader,” John Wiley & Sons, New York, 1994.
[24] C. R. Harvey, “Predictable Risk and Returns in Emerging Markets,” Review of Financial Studies, Vol. 8, No. 3, 1995, pp. 773-816.
NOTES
*We thank Pak Ho Leung and Liping Lu for able research assistance. All the remaining errors are ours. Webpage: http://www.cuhk.edu.hk/ eco/staff/tlchong/tlchong3.htm.
1Other empirical studies supporting technical analysis include Treynor and Ferguson [4], Kwon and Kish [5] and Chong and Lam [6].
2Other studies in this area include Ratner and Leal [17] and Chang, et al. [18].
3The acronym was coined by O’Neill [19].

