Technology and Investment
Vol.1 No.3(2010), Article ID:2491,9 pages DOI:10.4236/ti.2010.13020
Environmental Policy and Firm Investment Behaviour when Energy Saving Technologies are Available
University of Rome “Tor Vergata”, Rome, Italy
E-mail: gaeta@juris.uniroma2.it
Received June 8, 2010; Revised July 6, 2010; accepted July 12, 2010
Keywords: Environmental Policies, Fiscal Policies, Technological Change, Energy Saving, Welfare Analysis
Abstract
This paper investigates upon the effects of taxation on firm investment behaviour in presence of alternative energy (oil) saving technologies and scarce resources in competitive markets. Socially optimal policies are compared to a decentralized regulatory framework: the paper shows that taxation affects the adoption of different energy saving technologies hence the aggregate amount of energy saving. To our knowledge, there are few works that underline the relationship between environmental policies and firms’ incentives to adopt oil saving technologies. For this reason, we follow the theoretical literature focusing on the effects of environmental policy applied to pollution and climate change by adapting it to the energy saving perspective. We perform a static comparison of environmental policies to show that different levels of the same instrument lead to different results in terms of the number of firms adopting energy saving technologies; multiple equilibrium are possible but there is only one which is socially optimal.
1. Introduction
In the last decade, debates around environmental economics and policy have become increasingly permeated by issues related to technological change. One aspect of this issue relates to the effects that environmental policies have on firms’ behaviour. In particular the literature has focussed on the comparison of alternative policy instruments targeted to reduce social costs, paying specially attention to pollution and climate change, rather than to energy saving. There are few works underlining the relationship between environmental policy and firms’ incentives to adopt oil saving technologies and this paper follows such research line. In general, a large number of papers aim at establishing a ranking between alternative environmental policy instruments regarding the extent to which they enhance the adoption and diffusion of pollution control technology both at industry level [1-3] and firm level [4]. The goal in evaluating the different instruments is to compare the cost before and after adoption of the abatement technology, where the latter differs from a conventional “dirty” technology in terms of a lower marginal abatement cost [5]. However the literature is rather scattered: some authors focus on the ranking of market-based instruments by taking into account the time inconsistency of the environmental policy related to the delay between announcement and actual implementation [6,7]. Other authors investigate upon the effect that uncertainty—on the arrival time of the advanced technology—plays on firms’ choice, distinguishing by the case where the regulator anticipates or not the arrival of new technology.
Unlike the cited literature, this paper investigates upon the effects of taxation on firm investment behaviour in presence of alternative energy (oil) saving technologies and scarce resources in competitive markets. Socially optimal policies are compared to a decentralized regulatory framework: the paper shows that taxation affects the adoption of different energy saving technologies hence the aggregate amount of energy saving and decentralized policies are succesfull in achieving first best outcome [8,9]. The paper is strongly inspired by the theoretical analysis of Requate and Unold [4], but their research is focused on the comparison of policy instruments (taxes, auctions permits and standards) to reduce pollution in competitive markets rather than investigate upon the adoption of oil-saving technologies. They show that different policy instruments lead to quite different results in terms of emissions, if the number of firms which adopt the new technology is determined endogenously through equilibrium consideration.
Following their research, we try to define the optimal policy by comparing “market-based instruments”, to a “command-and-control” policy. Unlike the recent literature, we do not assume that all firms, belonging to the same industry, will adopt the new technology. Following Requate and Unold [4], we endogenize the number of adopting firms by analysing two scenarios that differ with respect to the order of first mover in a two-stage game: regulator—by setting the level of his policy instruments (e.g. tax rate)—or the firm by investing.
In the first one, called ex-ante optimal policy, we assume that the regulator makes a commitment both to the choice and level of his policy instrument. In this case the regulator moves at first, while the firms invest in the second stage, after observing the new tax rate and decide for the possible adoption of the new technology. In the second strategy, named ex post optimal policy, we are going to assume that, before the game starts, the regulator makes a commitment to the choice of his policy instrument only, although we are focusing on taxation only. Then she observes how many firms invest in the first stage and finally she chooses the level of the instrument. In the first case, for each implementation cost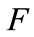 , a particular number of firms should invest for an optimal outcome. This would require coordination among firms. Since firms, however, are indifferent between investing and not when the tax rate equals the socially optimal marginal damage—which is a necessary condition for optimality—inefficient outcomes are likely to occur in this case. So, for the first scenario, we confirm the result found by Requate, Unold [4]: there are multiple equilibria, a lot of these are inefficient and the runic solution that can be pursued is the second best.
, a particular number of firms should invest for an optimal outcome. This would require coordination among firms. Since firms, however, are indifferent between investing and not when the tax rate equals the socially optimal marginal damage—which is a necessary condition for optimality—inefficient outcomes are likely to occur in this case. So, for the first scenario, we confirm the result found by Requate, Unold [4]: there are multiple equilibria, a lot of these are inefficient and the runic solution that can be pursued is the second best.
In the second situation, the planner moves after observing firms choice. In such a way the first best policy is a sub-game perfect equilibrium. Nevertheless, the implementation of such an equilibrium depends on the way the game is played between firms and planner. In such a case, Requate and Unold [4] find that there exists a unique subgame perfect equilibrium where the optimal number of firms invests and the regulator chooses the optimal tax rate. But firms move simultaneously and in an uncoordinated way, so nothing assures that the optimal number of firms investing in the advanced technology (first best) will be, in fact, implemented. Unlike Requate and Unold, [4], we are going to show that, if players act in a different way, the solution of first best will be implemented in a decentralized economy. This is possible in a “multi-stage game with observed actions and perfect information” [10] where the planner moves at the last stage and backward induction is a viable solution. This result can be considered as the original aspect of our paper (a previous investigation is found in Gaeta [11]), which makes a little but substantial difference with the research made by Requate and Unold [4].
This paper is organized as follows: In the next section, we discuss the characteristics of the model. Section 3 describes firms’ behaviour. In Section 4 we present the social optimum and derive the socially optimal allocation. In Section 5 we study two scenarios, in the first the regulator announces the instrument and fixes the relative level, while in the second she announces the instrument, but fixes the instrument in a second stage, after observing the firm’s behaviour. In Section 6 we present a numerical example which summarises the model. Conclusions follow in Section 7. Technical proofs are found in Appendix.
2. The Model
There are 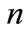 small firms operating in a competitive market. Every firm produces by means of a production function characterized by DRS, where the argument is oil (
small firms operating in a competitive market. Every firm produces by means of a production function characterized by DRS, where the argument is oil (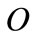 ). Under a laisser-faire policy, the firms choose the first best quantity
). Under a laisser-faire policy, the firms choose the first best quantity . Taxation on oil makes it expensive and firm are induced to substitute oil with an alternative input:
. Taxation on oil makes it expensive and firm are induced to substitute oil with an alternative input: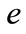 .
.
The firms can choose between two technologies: the first one, that we call conventional technology, is oil intensive, while the second one, called advanced technology, is “oil saving”. This means that, for the same output level, the advanced technology uses a lower level for  However, the implementation of the second technology is costly, according to a sunk cost
However, the implementation of the second technology is costly, according to a sunk cost . We are going to assume that each firm starts with the conventional technology.
. We are going to assume that each firm starts with the conventional technology.
We assume that oil price is given. This is so because the domestic oil demand is not able to affect the international oil price.
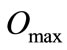 is the oil usage in the first best equilibrium, i.e. when the firms operate without taxation. With oil taxation, the level
is the oil usage in the first best equilibrium, i.e. when the firms operate without taxation. With oil taxation, the level 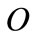 chosen by the firm can be reduced throughout an alternative input
chosen by the firm can be reduced throughout an alternative input . The
. The  usage depends on
usage depends on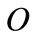 ,
, 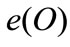 , with
, with ,
, 
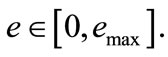 is the usage cost for
is the usage cost for 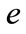 with
with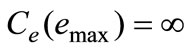 ,
,  It is helpful using
It is helpful using  as the unit of reference for the model and expressing
as the unit of reference for the model and expressing 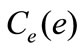 in terms of
in terms of  so we call
so we call  the substitution cost, between
the substitution cost, between  and
and  in terms of
in terms of  Given the relationship
Given the relationship 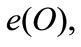 we conclude that
we conclude that ,
, ,
, 
Figure 1 highlights the relationship between  and
and .
.
The picture must be read clockwise: starting from a given  in the first diagram (e.g. C in the picture), we can obtain the implied level of
in the first diagram (e.g. C in the picture), we can obtain the implied level of  in the second one (the D point); the latter shows the assumed linear inverse relationship between
in the second one (the D point); the latter shows the assumed linear inverse relationship between  and
and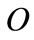 . The 45 degree line in the third diagram brings the point D in the fourth diagram. The latter shows the
. The 45 degree line in the third diagram brings the point D in the fourth diagram. The latter shows the  cost function. By linking the
cost function. By linking the 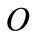 quantity with
quantity with  we obtain a point in
we obtain a point in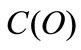 ; by iterating the proces we obtain the cost function in the
; by iterating the proces we obtain the cost function in the  space depicted in the first diagram.
space depicted in the first diagram.
Without taxation, the firm chooses the first best level of 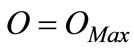 by using the conventional technology; this involves
by using the conventional technology; this involves 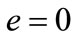 (point A).
(point A).
When two technologies are available the situation is the one shown in figure two. The first technology, that we call “conventional”, labeled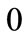 , is immediately available to firms free of additional implementation costs. The second one, that we call “advanced” and labelled
, is immediately available to firms free of additional implementation costs. The second one, that we call “advanced” and labelled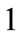 , is more efficient and allows firms to save
, is more efficient and allows firms to save  for each level of
for each level of 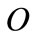 with respect the conventional technology; however firms adopting such a technology incur in a sunk cost
with respect the conventional technology; however firms adopting such a technology incur in a sunk cost . Figure 2 shows that
. Figure 2 shows that  and that
and that 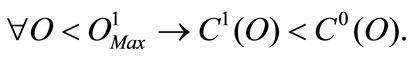 As an example, for a given
As an example, for a given 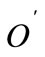 oil usage we have
oil usage we have .
.
Given the assumptions on the cost functions, the marginal oil saving costs 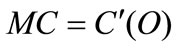 have the following characteristics:
have the following characteristics: 

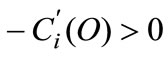 and strictly increasing in oil saving,
and strictly increasing in oil saving,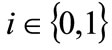

 . In other words, everytime the firm reduces the quantity O, the MC increases. It is worth stressing that, for the same
. In other words, everytime the firm reduces the quantity O, the MC increases. It is worth stressing that, for the same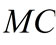 , i.e.
, i.e. 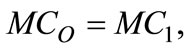 we have
we have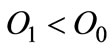 .
.

Figure 1. Energy saving costs with one technology.
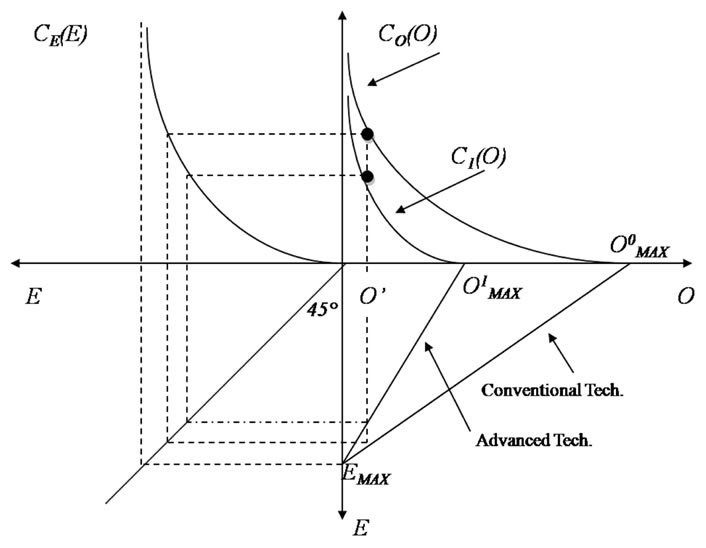
Figure 2. Energy saving costs with two technologies.
3. Equilibrium in Competitive Markets
We know that the solution of first best under competitive market conditions is to produce with the quantity 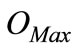 .
.
The profit function is:

where is the output price, normalized to one and
is the output price, normalized to one and  is the quantity in the first best situation.
is the quantity in the first best situation. 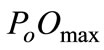 is the cost of using
is the cost of using  at the international price
at the international price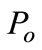 .
.
When oil taxation is at work, profits are as follows:

where 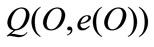 is the output quantity which depends on
is the output quantity which depends on 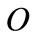 troughout
troughout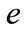 , while
, while 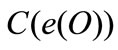 is the cost for oil saving and
is the cost for oil saving and  is the fiscal burden.
is the fiscal burden.
Let us rewrite the previous equation for the two technologies in this way:
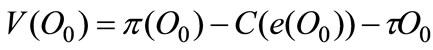

where  is the sunk cost of adopting the advanced technology.
is the sunk cost of adopting the advanced technology. 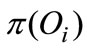 is the profit gross of tax and adjumest cost. By deriving with respect to
is the profit gross of tax and adjumest cost. By deriving with respect to 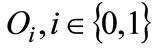 we obtain the following F.O.C.:
we obtain the following F.O.C.:
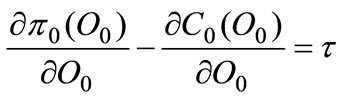 (1)
(1)
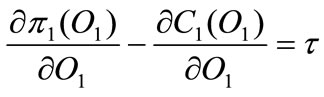 (2)
(2)
By taxing oil usage, the government induces firms to adopt or not the advanced technology. Now we are going to show that does exist only one tax rate that leaves firms indifferent in adopting or not.
By assuming technology satisfies  for a fixed
for a fixed , firms are indifferent to the adoption of new technology if:
, firms are indifferent to the adoption of new technology if:
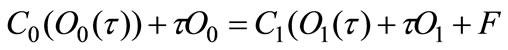 (3)
(3)
where 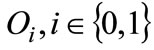 is the optimal oil usage under technology
is the optimal oil usage under technology  and
and 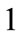 respectively. The indifference condition is quite simple: it claims that firms are indifferent when the costs of oil saving, inclusive of taxation, are equal under both technologies.
respectively. The indifference condition is quite simple: it claims that firms are indifferent when the costs of oil saving, inclusive of taxation, are equal under both technologies.
Lemma 1 shows that does exist  satisfating equation indifference:
satisfating equation indifference:
Lemma There exists at most one tax rate,  , such that firms are indifferent between adopting and not adopting the new technology. For this
, such that firms are indifferent between adopting and not adopting the new technology. For this , there exists a unique oil quantity
, there exists a unique oil quantity  and
and  chosen by the firms with and without advanced technology, respectively. If
chosen by the firms with and without advanced technology, respectively. If 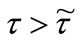 (
(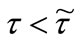 ) all firms (no firm) want to adopt the new technology. Moreover,
) all firms (no firm) want to adopt the new technology. Moreover,  is increasing in
is increasing in 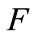 .
.
The proof is given in Appendix. Rationale is straightforwad. If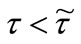 , the taxation is too low to induce firms to afford the sunk cost
, the taxation is too low to induce firms to afford the sunk cost 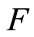 in order to adopt the advanced technology; no firm chooses to do that. The result is the maximum oil wasting in the economy, as all firms remain on the inefficient technology: it amounts to
in order to adopt the advanced technology; no firm chooses to do that. The result is the maximum oil wasting in the economy, as all firms remain on the inefficient technology: it amounts to  where
where 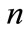 is the number of firms in the economy. Conversely, when taxation is sufficiently high,
is the number of firms in the economy. Conversely, when taxation is sufficiently high, it is too costly remaining with the conventional technology and all firms are induced to adopt the advanced one. In such a case the oil usage in the economy is lower than the previous case
it is too costly remaining with the conventional technology and all firms are induced to adopt the advanced one. In such a case the oil usage in the economy is lower than the previous case 
 Lemma 1 shows that between these two opposite case there exists an equilibrium of partial adoption, where firms are indifferent to adopt or not
Lemma 1 shows that between these two opposite case there exists an equilibrium of partial adoption, where firms are indifferent to adopt or not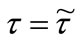 . The number of adopting firms is undetermined and the total oil usage in the economy lies in the closed set
. The number of adopting firms is undetermined and the total oil usage in the economy lies in the closed set .
.
4. Social Optimum
The previous lemma shows that the government is able to affect firms choice about the adoption of the technology. The amount of oil wasting in the economy is under the indirect control of central authority. If the government goal were to reduce the oil wasting in the economy it should fix a higher tax rate; as lemma 1 shows, in such a case, all firms invest in the new technology. Nevertheless this involves a private cost 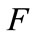 for each firm that reduces the social welfare. There is a trade-off between the private cost of increasing tax and the social benefit of oil saving induced by a high taxation. Hence, the social planner’s problem is to minimize the social costs by balancing industry’s total saving costs against the damage caused by the oil wasting. To do so, it chooses the optimal taxation filling the goal; this involves an optimal aggregate oil usage in the economy and a corresponding optimal number of adopting firms
for each firm that reduces the social welfare. There is a trade-off between the private cost of increasing tax and the social benefit of oil saving induced by a high taxation. Hence, the social planner’s problem is to minimize the social costs by balancing industry’s total saving costs against the damage caused by the oil wasting. To do so, it chooses the optimal taxation filling the goal; this involves an optimal aggregate oil usage in the economy and a corresponding optimal number of adopting firms . The social equilibrium is given by the triple
. The social equilibrium is given by the triple 
The social cost can be represented by a loss function  with
with 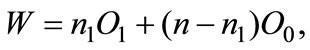 which evaluates the aggregate oil wasting in monetary terms. This implies that only aggregate oil wasting matters [4]. We assume that the damage function is increasing and convex in
which evaluates the aggregate oil wasting in monetary terms. This implies that only aggregate oil wasting matters [4]. We assume that the damage function is increasing and convex in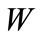 , i.e.
, i.e.  and
and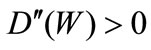 . If the regulator wants to minimize the social cost, she has to resolve this equation:
. If the regulator wants to minimize the social cost, she has to resolve this equation:
 (4)
(4)
The socially optimal allocation can be characterized as follows:
Proposition There is an interval of fixed costs 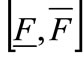 such that:
such that:
1) No firm should adopt the new technology for ;
;
2) All the firms should adopt the new technology for ;
;
3) For  partial adoption is optimal.
partial adoption is optimal.
The optimal number of firms  adopting the new technology is decreasing in
adopting the new technology is decreasing in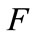 . The optimal marginal damage
. The optimal marginal damage  is decreasing in
is decreasing in .
.
The proof is given in Appendix. The intuition is that if the fixed cost 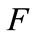 of installing the advanced technology is extremely high, firms do not adopt this technique. Conversely, if
of installing the advanced technology is extremely high, firms do not adopt this technique. Conversely, if 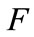 is sufficiently low, all the firms should adopt the new technology. In both cases, the optimal aggregate oil wasting
is sufficiently low, all the firms should adopt the new technology. In both cases, the optimal aggregate oil wasting 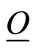 and
and 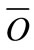 are independent of
are independent of .
.
5. Optimal Policy: Two Possible Scenarios
In this last section we are going to analyze how social planner can implement the socially optimal equilibrium. We are doing so by following two possible strategies. In the first one, called ex-ante optimal policy, we assume that the regulator makes a commitment both to the choice and level of his policy instrument. In this case the regulator moves at first, while firms invest in the second stage, after observing the tax rate, and decide for the possible adoption of the new technology. This is summarized in the following proposition:
Proposition (Ex ante optimal policy). If the welfaremaximizing regulator moves first, then: for 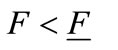 and
and 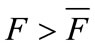 , there exits a unique subgame perfect equilibrium leading to a first best outcome. For
, there exits a unique subgame perfect equilibrium leading to a first best outcome. For  there are multiple equilibria. One of these equilibria is efficient but there are also many inefficient equilibria with too little and too much investment.
there are multiple equilibria. One of these equilibria is efficient but there are also many inefficient equilibria with too little and too much investment.
(See Appendix)
In the second strategy, ex post optimal policy, we are going to assume that, before the game starts, the regulator makes a commitment to the choice of his policy instrument only, so she observes firms investing in the first stage, then she chooses the level of the instrument in the second stage. Unlike the previous case, with such a strategy the socially optimal equilibrium can be implemented in the economy.
Proposition (ex post optimal policy). If the regulator sets his optimal policy after observing the number of investing firms, then under taxes there is a unique subgame perfect equilibrium where the optimal number of firms invests, and the regulator sets the first best tax rate.
The first part of the proposition follows Requate and Unold [4]. In a two stage game with informed and rational players, we can use the backward induction for proving the statement. In fact, firms know that, in the second stage of the game, the governement is going to set the optimal tax rate coherently with the optimal number of adopting firms  (first best). If
(first best). If 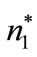 is chosen by firms in the first stage of the game, then this is a sub game perfect equilibrium as neither firms nor planner has an incentive to modify their choice. If firms choose
is chosen by firms in the first stage of the game, then this is a sub game perfect equilibrium as neither firms nor planner has an incentive to modify their choice. If firms choose 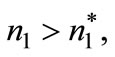 then the best strategy of the planner is to set the tax rate conditional on
then the best strategy of the planner is to set the tax rate conditional on 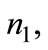 i.e.
i.e. 
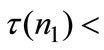 in the second stage, as the social damage reduce with respect to
in the second stage, as the social damage reduce with respect to 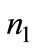 and tax must be reduced consequently. But this means that some firms that was adopting in stage 1 would be better off from not adopting, as the tax rate is lower than expected. So we conclude that
and tax must be reduced consequently. But this means that some firms that was adopting in stage 1 would be better off from not adopting, as the tax rate is lower than expected. So we conclude that 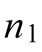 is not an equilibrium. Same result holds when
is not an equilibrium. Same result holds when 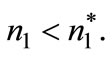 Nevertheless, the game analyzed by Requate and Unold [4] shows only that an equilibrium exists under subgame perfection, but this does not imply that such equilibrium will be effectively implemented. Unlike Requate and Unold [4], we are going to show that, if players act in a different way,
Nevertheless, the game analyzed by Requate and Unold [4] shows only that an equilibrium exists under subgame perfection, but this does not imply that such equilibrium will be effectively implemented. Unlike Requate and Unold [4], we are going to show that, if players act in a different way,  will be implemented in a decentralized economy. This is possible in a “multi-stage game with observed actions and perfect information” [10]. In such a game, the choice set of each player is enlarged by the move “do nothing”. As an example, any single firm strategy set, per each game stage, is composed by
will be implemented in a decentralized economy. This is possible in a “multi-stage game with observed actions and perfect information” [10]. In such a game, the choice set of each player is enlarged by the move “do nothing”. As an example, any single firm strategy set, per each game stage, is composed by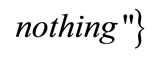
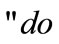
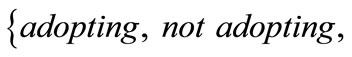 . Moreover, any player knows the history of the game, as everyone observes past actions.
. Moreover, any player knows the history of the game, as everyone observes past actions.
We say that a multi-stage game has perfect information if, for every stage  and history
and history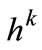 , exactly one player has a nontrivial choice set—a choice set with more than one element—and all the others have the one-element choice set “do nothing” [10].
, exactly one player has a nontrivial choice set—a choice set with more than one element—and all the others have the one-element choice set “do nothing” [10].
The planner moves at the last stage, so backward induction is still a viabile solution. Everyone knows the optimal taxation level chosen by the planner at the last stage of the game as consequence of  The game is composed by
The game is composed by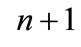 stages. At each stage one firm chooses whether adopting or not, knowing what happened up to now; the other one choose “do nothing”. Once the single firm has played either “adoption” or “not adoption” it will choose “do nothing” in the rest of the game. In such a way, when
stages. At each stage one firm chooses whether adopting or not, knowing what happened up to now; the other one choose “do nothing”. Once the single firm has played either “adoption” or “not adoption” it will choose “do nothing” in the rest of the game. In such a way, when  has been achieved in the economy it becomes common knowledge, as everyone knows the past history of the game. From now and on, rational firms do choose “not adopting” as they know that if
has been achieved in the economy it becomes common knowledge, as everyone knows the past history of the game. From now and on, rational firms do choose “not adopting” as they know that if 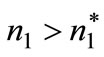 the taxation rate chosen by the planner at the last stage is not choerent with their choice, following the reasoning of the sub-game perfection used for the first part of the proposition..
the taxation rate chosen by the planner at the last stage is not choerent with their choice, following the reasoning of the sub-game perfection used for the first part of the proposition..
6. A Numerical Example
In this section we discuss a numerical example to show in detail the mechanism of the model.
We know that the firm can choose between two techniques that are characterized by different costs.
For each technology, the firm supports an energy saving cost: . We suppose that this kind of cost functions has the following explicit form, choerently with the assumptions described in Section 1:
. We suppose that this kind of cost functions has the following explicit form, choerently with the assumptions described in Section 1:

Figure 3. Oil saving costs.
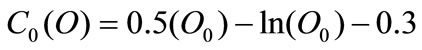 “oil intensive”
“oil intensive”
 “advanced technology “
“advanced technology “
These functions are depicted in Figure 3, which corresponds to the graph of the first diagram reported in Figure 2.
As shown by the graph, for each technique, we obtain a monotonic decreasing function on its closed domain, that describes the negative relationship between the energy saving costs: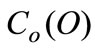 ,
, 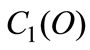 and the oil quantity.
and the oil quantity.
The marginal energy saving costs:  and
and 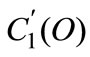 are described by the two functions presented in Figure 4, where,
are described by the two functions presented in Figure 4, where,  and
and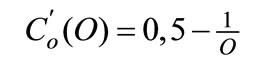 and they respect the assumptions made in Section 2.
and they respect the assumptions made in Section 2.
Now, we give a numerical explanation of Lemma 1.
The Figure 5 shows that for a fixed F, there exists at most one tax rate, such that firms are indifferent between adopting and not adopting the new technology. In fact, for 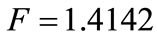 there is only intersection point that individuates:
there is only intersection point that individuates:  that satisfies the indifference condition.
that satisfies the indifference condition.
If we vary , we can observe the positive relation between
, we can observe the positive relation between  and
and , as shown by Table 1.
, as shown by Table 1.
By proposition 2, we know that if the new technology is available, the social planner seeks to minimize total social costs expressed by the equation lagra which is a numerical example of the equation lagrth.
By assuming 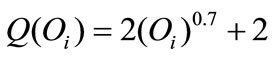 the Lagrangian that solves this problem is reported in the following equation:
the Lagrangian that solves this problem is reported in the following equation:
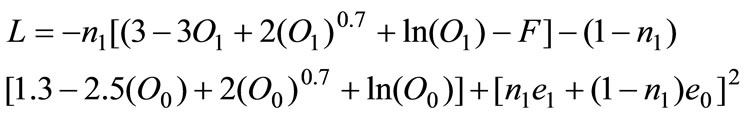
This numerical example shows the existence of the values of first best: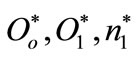 .
.
The Table 2 shows the content of proposition 2.
If we vary , we can observe that there is an interval of fixed costs
, we can observe that there is an interval of fixed costs 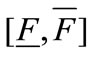 such that for:
such that for:
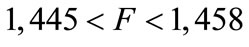 we obtain
we obtain , so there is partial adoption, while for
, so there is partial adoption, while for 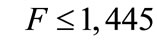 or
or 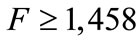 we observe corner solutions.
we observe corner solutions.
7. Conclusions
The paper shows the existence of an optimal policy that reduces the social cost represented by oil usage. The regulator can implement this policy throughout two alternative strategies: the ex ante optimal policy or the ex post optimal policy. The choice depends on the sunk cost of

Figure 4. Marginal energy saving costs.

Figure 5. Lemma 1.

Table 1. Relationship between  and
and .
.

Table 2. Proposition 2.
adopting the oil saving technology. If the implementation cost is outside the range 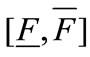 the regulator is indifferent between the two strategies: both strategies lead to the first best. If the implementation cost is within the range, the regulator can implement the optimal policy only by choosing the ex post optimal policy, where firms move according to a multi-stage game with informed and rational players. So the paper confirms that policies ruled by the market are viable instruments for environmental control. We also show that, unlike the current literature, first best solution is actually implemented when firms and the regulator play a sequential game.
the regulator is indifferent between the two strategies: both strategies lead to the first best. If the implementation cost is within the range, the regulator can implement the optimal policy only by choosing the ex post optimal policy, where firms move according to a multi-stage game with informed and rational players. So the paper confirms that policies ruled by the market are viable instruments for environmental control. We also show that, unlike the current literature, first best solution is actually implemented when firms and the regulator play a sequential game.
The sunk cost 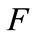 plays a leading role for results; in a following paper we are going to investigate how results change when such a cost is made endogenous by assuming an R&D sector in the economy.
plays a leading role for results; in a following paper we are going to investigate how results change when such a cost is made endogenous by assuming an R&D sector in the economy.
8. References
[1] P. B. Downing and L. J. White, “Innovation in Pollution Control,” Journal of Environmental Economics and Management, Vol. 13, No. 1, 1986, pp. 18-29.
[2] S. R. Milliman and R. Prince, “Firms Incentives to Promote Technological Change in Pollution Control,” Journal of Environmental Economics and Management, Vol. 17, No. 3, 1989, pp. 247-265.
[3] Ch. Jung, K. Krutilla and R. Boyd, “Incentives for Advanced Pollution Abatement Technology at the Industry Level: An Evaluation of Policy Alternatives,” Journal of Environmental Economics and Management, Vol. 30, No. 1, 1996, pp. 95-111.
[4] T. Requate and W. Unold, “Environmental Policy Incentives to Adopt Advanced Abatement Technology: Will the True Ranking Please Stand up?” European Economic Review, Vol. 47, No. 1, 2003, pp. 123-146.
[5] T. Requate, “Dynamics and Incentives by Environmental Policy Instruments—A Survey,” Ecological Economics, Vol. 54, No. 2-3, 2005, pp. 175-195.
[6] D. P. van Soest, “The Impact of Environmental Policy Instruments on the Timing of Adoption of Energy-Saving Technologies,” Resource and Energy Economics, Vol. 27, No. 3, 2005, pp. 235-247.
[7] A. von Döllen and T. Requate, “Environmental Policy and Incentives to Invest in Advanced Abatement Technology if Arrival of Future Technology is Uncertain,” Economics Working Paper No 2007-04, 2007.
[8] J. Montero, “Permits, Standards, and Technology Innovation,” Journal of Environmental Economics and Management, Vol. 44, No. 1, 2002, pp. 23-44.
[9] C. Carraro and D. Siniscalco, “Environmental Policy Reconsidered: The Role of Technological Innovation,” European Economic Review, Vol. 38, No. 3-4, 1994, pp. 545-554.
[10] D. Fudenberg and J. Tirole, “Game Theory,” MIT Press, Cambridge, 1991.
[11] E. G. Gaeta, “Environmental Policy, Innovation and Adoption of Energy Saving Technologies,” Phd Dissertation, University of Rome, “La Sapienza”, 2009.
Appendix
Proof of Lemma 1
Now we focus on the total difference of the net value of the i- firm:
firm:
 A.1
A.1
So we can write A.1 as follows:
 A.2
A.2
respect to  to demonstrate that there exists at most one tax rate such that firms are indiferent to adption or not adoption.
to demonstrate that there exists at most one tax rate such that firms are indiferent to adption or not adoption.
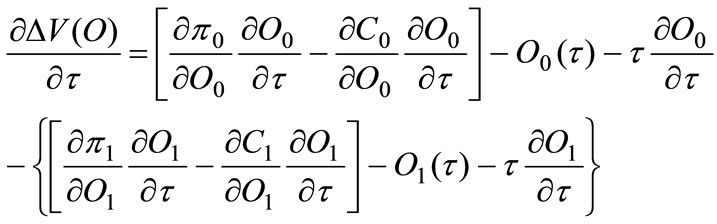 A.3
A.3
substituting Equations (1), (2) into A.3 we obtain:
 A.4
A.4
which is always negative, because as previously stressed, the same MC involves 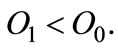
When since
since
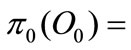 by the competitive market assumtion. We know that
by the competitive market assumtion. We know that 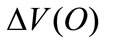 is a monotonic function and it decreases if
is a monotonic function and it decreases if  increases, as A.4 shows; this means that there is a unique
increases, as A.4 shows; this means that there is a unique  called
called  which ensures that firms are indifferent between the two technologies, i.e. when
which ensures that firms are indifferent between the two technologies, i.e. when .
.
Now we demonstrate that  is increasing in
is increasing in  .
.
Differentiating the net value A.2 with respect to  and remembering the F.O.C., we obtain:
and remembering the F.O.C., we obtain:


which is always positive because, as previously stressed, . This result demonstrates that
. This result demonstrates that 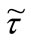 is increasing in F.
is increasing in F.
Proof of Proposition 2:
The Lagrangian of the minimization problem is given by:
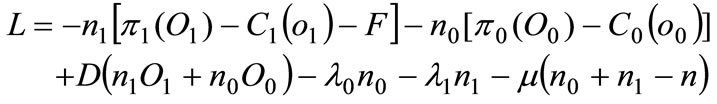 A.5
A.5
where 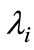 are the Kuhn_Tucker multipliers of the non negative constraints for
are the Kuhn_Tucker multipliers of the non negative constraints for 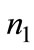 and
and  We denote
We denote 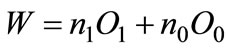 as the total use of oil choosen by firms under taxation. Differentiating the A.5 respect to
as the total use of oil choosen by firms under taxation. Differentiating the A.5 respect to 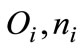 we obtain the first order conditions:
we obtain the first order conditions:
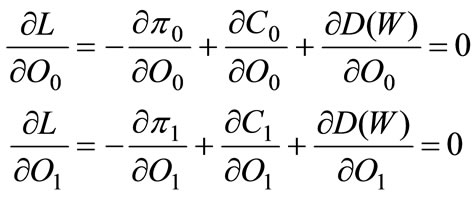 A.6
A.6


eliminating  yields:
yields:
 A.7
A.7
First, suppose that there exists an interior solution, i.e. 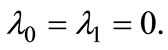
Differentiating system A.6 and A.7 w.r.t.  and using the chain rule in A.7 we have the following equations:
and using the chain rule in A.7 we have the following equations:

 A.8
A.8
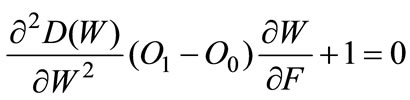
Given that  we can write
we can write
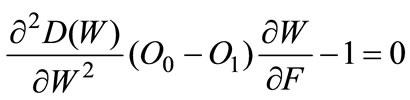
This yields
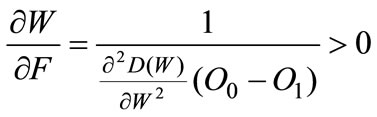 A.9
A.9
i.e. optimal aggregate use of oil is increasing in F. Substituting A.9 into A.8 yields:
 A.10
A.10
Unlike Requate and Unold [4] the Equation A.10 is negative only if: 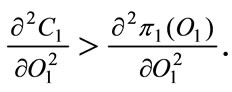 and we assume this condition holds. So we have:
and we assume this condition holds. So we have: 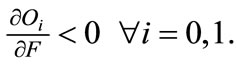 Hence, optimal use of oil by each firm is decreasing in F.
Hence, optimal use of oil by each firm is decreasing in F.
Now total energy wasting can be written as
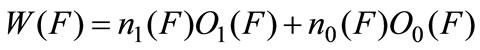 A.11
A.11
Differentiating A.11 w.r.t. F and solving for  yields:
yields:
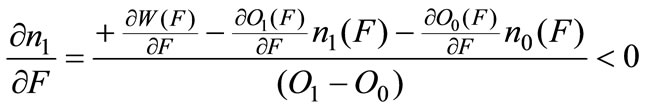
From Equation A.7 we know that
 A.12
A.12
If  is large, the LHS of the A.12 is positive since that
is large, the LHS of the A.12 is positive since that 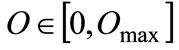 so we have
so we have  and
and
 So, when F is large, there exists an
So, when F is large, there exists an 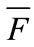 such that if
such that if  no firm should adopt the advanced technology.
no firm should adopt the advanced technology.
Let us rewrite Equation A.12 in the following way:
 A.13
A.13
if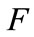 is very small we have
is very small we have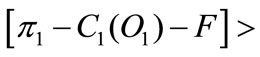
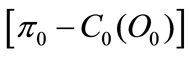 and the LHS of Equation A.13 is positive. This involves
and the LHS of Equation A.13 is positive. This involves  that means
that means  So when F
So when F there exists an
there exists an 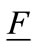 such that if
such that if  all firms adopt the advanced technology.
all firms adopt the advanced technology.
So far we have demonstrated that 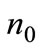 (and consequently
(and consequently  is one for
is one for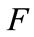 large and zero for
large and zero for 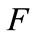 small. However, being the functions of Equation A.13 continuos is
small. However, being the functions of Equation A.13 continuos is there exist values for
there exist values for such that both
such that both  and
and 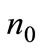 are outside the corner solutions:
are outside the corner solutions: 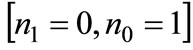 and
and 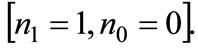 So we conclude that for
So we conclude that for we have
we have 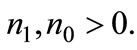 In this case there is partial adoption.
In this case there is partial adoption.
Proof of Proposition 3:
When the regulator chooses the instrument (taxation) and fixes the instrument’s level in the same time, there are three possible cases:
1) 
We have shown that in such a case  and
and 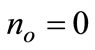 this means that F.O.C for the Equation A.5 involves :
this means that F.O.C for the Equation A.5 involves :

but for the firm F.O.C. we know that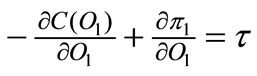 . So finally, the government sets
. So finally, the government sets 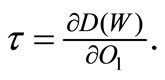 By so doing, the optimal taxation is coherent with firm profit maximization and there is a subgame perfection.
By so doing, the optimal taxation is coherent with firm profit maximization and there is a subgame perfection.
2) 
Similar analysis holds. In such a case  and
and  this means that F.O.C for the Equation A.5 involves :
this means that F.O.C for the Equation A.5 involves :

but for the firm F.O.C. we know that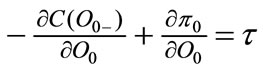 . So finally, the government sets
. So finally, the government sets  and the strategy is subgame perfect .
and the strategy is subgame perfect .
3) 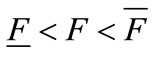
In this case the regulator sets  by minimizing Equation A.5. This involves a particular value for
by minimizing Equation A.5. This involves a particular value for 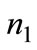 and
and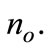 Nevertheless as firms play in the second stage in an uncoordinated way, there is no certainty that
Nevertheless as firms play in the second stage in an uncoordinated way, there is no certainty that 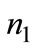 and
and  will be effectively implemented. For the same reason, is possible that, for pure chance, firms choose
will be effectively implemented. For the same reason, is possible that, for pure chance, firms choose 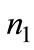 and
and 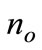 coherently with the optimal value chosen by the government. Hence multiple equilibria are possible, but only one is the efficient one.
coherently with the optimal value chosen by the government. Hence multiple equilibria are possible, but only one is the efficient one.
NOTES
*I am indebted to the IAD—University of Rome Tor Vergata (http: www. scuolaiad.it) that provides funds for my research.

