Journal of Electromagnetic Analysis and Applications
Vol.08 No.04(2016), Article ID:65948,16 pages
10.4236/jemaa.2016.84009
New 3D Aware Formulation of MoM-GEC Method for Studying Planar Structures with Vertical Sources
Oueslati Basma, Ben Salah Taha, Larbi Chiraz, Aguili Taoufik
Communication System Laboratory Sys’Com, National Engineering School of Tunis, University Tunis El Manar, Tunis, Tunisia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 March 2016; accepted 24 April 2016; published 27 April 2016
ABSTRACT
This paper proposes a generalization of the MoM-GEC method [1] needed for studying planar structures excited with a source located at perpendicular plan relative to circuit plan. A general formulation is detailed to allow modeling excitation of a planar structure with one or more sources located in plans other than the circuit plan. The numerical approach elaborated is based on the definition of new admittance operators and rotational transformations describing the transition from one plan to another. To validate this approach, we consider the case of a single source located in the perpendicular plan to the circuit.
Keywords:
Admittance Operator, MoM-GEC 3D, Discontinuities, Vertical Source

1. Introduction
Studying of microwave planar circuits is based on EM characterization of the structure via determination of electrical (E) and magnetic (H) fields and the electric current density J using Maxwell equations. To solve these equations, iterative methods are used (FDTD [2] [3] and FEM [4] [5] ) providing accurate results but requiring a relatively heavy calculation time [6] . To overcome this disadvantage, integral methods have been proposed. Integral equations introduce an excitation term in the integral formulation of an electromagnetic problem that needs to establish an appropriate mathematical model: source model [7] .
As the source is the knowledge of an electromagnetic field distribution on a circuit surface independently of the load, one distinguishes two source models: localized source modal [8] [9] and extended source modal [6] [7] defined in the perpendicular plan to the circuit. The source can be considered as a discontinuity causing the creation of higher order modes at the border source/circuit [10] - [15] . This discontinuity can be corrected by using a coupling quadripole [8] [16] - [18] . That generates an additional computing time. Considering the fundamental mode of the access line can be an optimized solution which allows us to have a perfect adaptation between source and circuit [19] [20] .
Localized source remains a theoretical and relatively simple model to describe studied structure. Such model, is not fully consistent with actual excitations located in another plan than the circuit which favors the extended source, hence the importance of our study.
Our goal is to develop an exact source method based on MoM-GEC method for studying planar structures excited by sources located in any other plan. We first establish a general formulation for the case of N sources. We verify, then the accuracy of the hypothesis of sources simplification: localized planar sources.
3D extension of MoM-GEC method has not been really focused on in previous work. Related work mainly includes Hamdi et al. work in [13] . However, this work focused on input impedance and scattering matrix evaluation rather than a full EM characterization. In our study, we define new admittance operators to bind excitation sources to electrical quantities defined in the circuit plan and thus help calculate EM fields accurately. We also introduce a new rotational transformation describing the transition from one plan to another. The determination of these operators is important because it allows us to perform three-dimensional calculation while keeping homogeneous the MoM-GEC method (decomposition of operators on the TE and TM modes).
In this paper, input impedance, current density and electric field distribution are evaluated and discussed in the case of a single vertical source. Results are compared to commercial software HFSS and CST. A couple of structures are studied: microstrip short-circuited line and microstrip open circuit line as an application.
This paper is organized as follows: we start presenting the new approach in the case of N sources by exposing the general formulation of integral equations to determine the admittance matrix. Then, we detail the formulation and the determination of input admittance (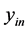 ) in the case of a single extended source located at the perpendicular plan to circuit. In Section 4, we focus on determining admittance operators. Finally, in Section 5 we present different simulations results obtained for the two studied structures.
) in the case of a single extended source located at the perpendicular plan to circuit. In Section 4, we focus on determining admittance operators. Finally, in Section 5 we present different simulations results obtained for the two studied structures.
2. New Formulation of MoM-GEC Method for 3D Structures
In this section, we introduce and explain the general formulation for 3D structures by considering the case of N-ports (N sources) located at perpendicular plans to the circuit. Figure 1 shows the general structure excited by
Figure 1. Planar structure with N discontinuities (N sources).
voltage sources (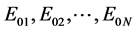 ). The electromagnetic analysis of this structure consists in solving an integral equation expressing the boundary conditions of electromagnetic fields of sources and circuit plans. This equation has the following form:
). The electromagnetic analysis of this structure consists in solving an integral equation expressing the boundary conditions of electromagnetic fields of sources and circuit plans. This equation has the following form:
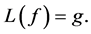 (1)
(1)
where L is an integro-differential operator, g is the excitation source and f is the unknown to be determined.
In this work, L is an admittance operator, f is the electric field E tangential to the circuit plan and g represents the excitation sources. The method consists in solving this equation by the Galerkin method (a variety of the MoM method) to determine the electric field E and deduce the input admittance 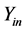 matrix
matrix
The circuit is printed on a dielectric substrate of relative dielectric constant 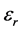 with a thickness h. N transmission lines feed the structure defining N discontinuities. Each transmission line is excited with a vertical port. Discontinuities at port level is overcome by considering fundamental mode of the transmission line.
with a thickness h. N transmission lines feed the structure defining N discontinuities. Each transmission line is excited with a vertical port. Discontinuities at port level is overcome by considering fundamental mode of the transmission line.
To characterize this discontinuity, we used the formalism of admittance operator and assume that excitation sources are totally independent and completely decoupled (electromagnetic coupling) for each other [21] [22] . It would be necessary to determine with precision the fundamental mode of the attachment lines to ensure good adaptation.
The electromagnetic quantities in source plans (from P1 to PN) and planar circuit (c) are expressed in following relations (Equation (2)):
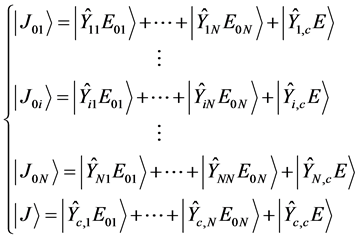 (2)
(2)
where:
 (i = 1 to N): current density of the source (i).
(i = 1 to N): current density of the source (i).
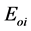 (i = 1 to N): Electric field of the source (i).
(i = 1 to N): Electric field of the source (i).
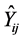 (i = 1 to N + 1, j = 1 to N + 1): Admittance operators with the (N + 1)th plan is the circuit plan.
(i = 1 to N + 1, j = 1 to N + 1): Admittance operators with the (N + 1)th plan is the circuit plan.
E and J are the electric field and the current density defined in the circuit plan.
The admittance operators 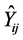 define the relationship between the electric fields of TE and TM modes from the jth plan and the current density generated by these modes on the ith plan provided that all sources k # j are switched off and the circuit plan is metallized. These
define the relationship between the electric fields of TE and TM modes from the jth plan and the current density generated by these modes on the ith plan provided that all sources k # j are switched off and the circuit plan is metallized. These 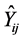 can be determined by applying the superposition theorem to the Equation (2) and decomposing these operators on a homogeneous basis (TE and TM) associated to each plan defining the different electromagnetic quantities.
can be determined by applying the superposition theorem to the Equation (2) and decomposing these operators on a homogeneous basis (TE and TM) associated to each plan defining the different electromagnetic quantities.
If 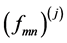 and
and 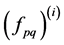 are a decomposition orthonormal basis of the electric field and current density defined on the plans i and j, then for;
are a decomposition orthonormal basis of the electric field and current density defined on the plans i and j, then for; 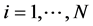 and
and


For modeling the electric field E of the circuit plan, we choose test functions of electric field type

With 
Test functions satisfy the boundary conditions of the circuit plan. They are zero on the metal and non-zero on the dielectric. And conversely, the current density J defined on the circuit plan is zero on the dielectric and non- zero on the metal. Therefore, the test function 

The application of the Galerkin method to the Equation (2) involves projecting the first N equations respectively on the unitary sources functions from 

We suppose that: 

With
Considering the orthonormalization relationships verified by these unitary sources: (where 

With:





The determination of the admittance matrix 




In this section, we presented a general formulation of the problem by taking the case of N vertical sources. By applying the Galerkin method, we determined the admittance matrix binding current density and E field. This matrix is characterized by new admittance operators describing the transition from one plan to another. To validate our approach, we develop in this paper the case of a single vertical source that is the subject of the next section.
3. Single Vertical Source Case
The vertical source located at perpendicular plan to the circuit is the most used excitation source in real conditions. We focus now on the study of a single vertical source located at the perpendicular plan to the circuit. We start presenting the studied structures. Then, we detail the determination of the admittance operators.
3.1. Studied Structures
To validate our method, we consider two structures: a micro-strip short-circuited line Figure 2(a) and a microstrip open circuit line Figure 2(b). The choice of the first structure is argued by the fact that the estimated theoretical impedance of this structure is known which allows us to validate the obtained input impedance. The


Figure 2. Studied structures: (a) Microstrip short-circuited line; (b) Microstrip open circuit line.
second structure allows us to verify the boundary conditions and to ensure the validity of the numerical approach.
Table 1 and Table 2 illustrate the dimensions of the two structures enclosed in a box.
With: 
lp: length of the microstrip line,
ls: length of the dielectric substrate,
lb: length of the box,
Table 1. Microstrip short-circuited line dimensions.
Table 2. Microstrip open circuit line dimensions.
wp: width of the microstrip,
a: width of the box/dielectric substrate,
h0: thickness of the dielectric substrate,
h: thickness of the box.
By using the generalized equivalent circuit method, we can model each of the two structures of the Figure 2 with the following equivalent circuit (Figure 3).
The circuit is excited by a single source of electric field type. This source is defined by a unitary function







With: 


To determine the electric field
3.2. The Input Admittance of a Discontinuity Port
Using the formulation of the source method developed in the Section 2, the current densities of the source and the circuit are associated to the corresponding electric fields by the admittance operators:

Applying the same procedure in (2), the Galerkin method is used to solve Equation (16) while taking into account the boundary conditions of electromagnetic fields on the circuit plan. The first step in the Galerkin method is to define test functions 


The test functions 
Figure 3. Equivalent circuit of the studied structure.
plan (xoz) (Equation (18)).

where:





The second step is to project the Equation (1) of the System (16) on the unitary function 


With:




To calculate the input admittance, we must determine the different admittance operators: 

4. Admittance Operators
To calculate the different operators, we need to impose some conditions, namely:
The 



Similarly, the 



This procedure is ensured after establishing in each plan (xoy) and (xoz) a basis of TE and TM mode functions satisfying the boundary conditions and allowing the decomposition of operators
We explain in the next two paragraphs the determination method of the operators 

To have an equation system containing only the two operators 



Hence the circuit plan split the structure into two homogeneous areas separated by an electric wall. In the straight section of each guide, basis functions 

The mode functions TE and TM in the plan (xoy) are given by the Equation (25) and Equation (26):


With:

The propagation constant of the mode 


4.1. Determination of the 
The decomposition of the 



With:




4.2. Determination of the 
The operator 
In fact, knowing the electric field in the source plan (xoy) which is decomposed on the mode functions

axes (ox) and (oy), we use the following relationship:
The third component of 

Equation (32) presents the relationship binding the operator 


To describe the operator



Similarly, we can describe the field E1 on the basis of mode functions 

Using the Equation (34), we can express the current 


By identification (Equation (33) and Equation (35)), the current 

Using Equation (33) and the fact that 

From the Expression (37), we deduce the expression of the 

With:

We define 

By substituting the expression of E1 (Equation (34)) in the expression of 

By identification between Equations (36) and (41), we can deduce the expression of the new operator 

After expressing the different operators and transformations, the next section will be dedicated to numerical results for two chosen structures and make some comparisons to validate our new approach.
5. Numerical Results
The new numerical approach is based on the definition of several admittance operators used to describe the passage from one plan to another. The implementation of these operators require several large-sized matrices manipulation and cpu-consuming integral calculations. In our case, using development environments dedicated to numerical calculations such as MATLAB is not suitable, lacks of fast hybrid symbolic/numeric calculation and has no built-in cache support neither save-points concept (we cannot resume calculation when needed).
There are several alternatives, namely programming languages: C, C++ and Java. In literature, several researchers recommended JAVA for scientific treatment [23] - [25] due to its robustness, automatic memory management and portability.
In our research laboratory SYS’COM, DrTaha Ben Salah has developed during his research work a TMWLib library (for Tiny MicroWave Library) [26] . This library is based on Java/Scala programming languages, is fully modular, feature rich and scalable. Also, it enables fast hybrid symbolic/numerical calculation and cache/save- point concept.
We applied our modelling approach to both structures: microstrip short-circuited line and microstrip open circuit line. We used the microstrip short-circuited line as a reference structure to compare obtained input impedance with theoretical input impedance of this structure. We also deduce for these structures some electromagnetic characteristics (current density J and electric field E) to verify the boundary conditions.
5.1. Input Admittance of Microstrip Short-Circuited Line
The chosen studied structure to validate the obtained input impedance is a microstrip short-circuited line. This structure must respect two approximations. First, the structure is considered as a transmission line submitted to the line’s fundamental mode (characterized by its propagation constant βg). Then, the line length L should be large enough to assume that higher order modes reflected at the short circuit are attenuated before reaching excitation source. The expected value of the theoretical input admittance is given by the Equation (43).

With 
Figure 4 illustrates the simulation result of the input impedance 

Figure 4. Comparison between the calculated and theoretical input admittance for microstrip short-circuited line.
functions (trigonometric type), 94,000 TE and TM mode functions 

We observe that the two curves of the input impedance are very close with a relative error lower than 1%. This confirms the validity of our numerical approach and the perfect adaptation between source and circuit. In fact, among the parameters affecting the consistency of results precision of the fundamental mode taken as excitation source has the higher effect.
With X is the length l of the microstrip line.
5.2. Electromagnetic Characteristics of Microstrip Short-Circuited Line
In this section, we present some electromagnetic characteristics (current density and electric field) for a microstrip short-circuited line. We also compare the obtained results to the results found with two commercial software HFSS and CST.
Figure 5 illustrates shapes of the current density (HFSS, CST and MoM-GEC’3D). We observe that the three curves have the same variation of the current which satisfies the boundary conditions. This result is very consistent with excepted values for a short-circuited line for the specified dimensions.
Figure 6 and Figure 7 illustrate the shape of the electric field Ey along the propagation direction (oy). We note that the electric field satisfies the boundary conditions. It is maximum at the source and presents a fast attenuation at source/line discontinuity. The result with the new approach MOM-GEC’3D contains small attenuation that tend to cancel due to the Gibbs effect. HFSS gives a less step attenuation at source/line discontinuity; whereas CST’s result has the best consistency
Figure 8 allows to verify the boundary conditions for the electric field Ex. The two figures obtained with CST and MoM-GEC’3D confirms results alignment.
5.3. Electromagnetic Characteristics of Microstrip Open Circuit Line
In this section, we present results of current density and electric field for a microstrip open circuit line to validate our numerical approach.

Figure 5. Current density comparison between: (a) HFSS; (b) CST and (c) MoM-GEC’3D.
Figure 6. Electrical Field Ey comparison between: (a) HFSS; (b) CST and (c) MoM-GEC’3D: section along axis (ox).

Figure 7. Electrical Field Ey comparison between: (a) HFSS; (b) MoM-GEC’3D and (c) CST: 2D view.
Figure 9 and Figure 10 present the current density. We note that the three results obtained with MoM- GEC’3D, HFSS and CST are very consistent. At convergence MoM-GEC’3D and CST present better results when considering EM symmetry of the structure (along ox axis). Besides, line width is small when compared to

Figure 8. Electrical Field Ex comparison betweenMoM-GEC’3D and CST.

Figure 9. Current density Jy comparison between: (a) MoM-GEC’3D; (b) HFSS and (c) CST.
Figure 10. Current density Jy comparison between MoM-GEC’3D and CST: section along (ox) axis.
wavelength, variations along (x) should not be relevant, which is the case of (a). Still CST have some important variation (at the center of the line). Moreover, a better attenuation (Figure 10) is remarkable with small Gibbs effect lead us to conclude that new approach gives more rigorous results.
Figure 11 and Figure 12 illustrate that the electric field for the 3 simulation results verify the boundary conditions. We note also that the curve of MOM-GEC’3D contains small attenuation due to Gibbs effect. We may add an artificial additional term to compensate this effect and reduce numerical errors. Figure 12 gives even better confirmation of result validation as one can appreciate good attenuation of numerical results of Ey away from source and magnetic wall (line edge). Again, MoM-GEC’3D gives better results but still very similar to
Figure 11. Electrical Field Ey section along (oy): comparison between MOM-GEC’3D, CST and HFSS.

Figure 12. Electrical Field Ey comparison between (a) MOM-GEC’3D, (b) HFSS and (c) CST.
CST while HFSS gives a little more fuzzy results. All of three results still consistent with boundary conditions though.
Similarly, the electric field component Ex verifies the boundary conditions for the result obtained with MOM-GEC’3D and CST while CST, for this case, presents a better boundary conditions. This may be explained with the forced usage of (y) based test functions (in order to validate more generic approach) whereas line width is too small relatively to wavelength, so that Gibbs effect remains a little substantial (Figure 13).
The different simulations made for short circuit and open circuit demonstrates the accuracy of our new approach. This was approved by the verification of the boundary conditions and comparison with two commercial simulation software HFSS and CST.
6. Conclusions
In this paper, we present a new formulation of the source method to characterize discontinuities in planar circuits. A new definition of the excitation source is introduced to overcome the discontinuity problem at the source/circuit transition. We expose a general formulation of the source method, by determining the Input admittance matrix of N-port discontinuity in a planar circuit. To validate our approach, we considered the case of a single vertical source. We detailed the determination of the various operators and rotational transformations required to calculate the input impedance. In the last part of our work, we presented and interpreted some results in the case of a microstrip short-circuited line and microstrip open circuit line.
The numerical results obtained using this approach were compared to results obtained by both commercial software HFSS and CST. Our results show a concordance and consistency with those obtained using HFSS and CST, with even better results in most cases.
We also demonstrated that considering the fundamental mode of the access line to circuit as the excitation source gives us a perfect adaptation between the source and the circuit.
This new approach can be applied to any type and number of excitation sources (coaxial cable at perpendicular plan [27] or coaxial line located in the ground plan, etc). The originality of this work lies mainly in the new

Figure 13. Electrical Field Ex comparison between MGEC and CST: 2D view.
definition of the source in the integral analysis and the determination of admittance operators to link the electromagnetic quantities of sources and magnitudes of the circuit, which are defined in vertical plans.
Cite this paper
Oueslati Basma,Ben Salah Taha,Larbi Chiraz,Aguili Taoufik, (2016) New 3D Aware Formulation of MoM-GEC Method for Studying Planar Structures with Vertical Sources. Journal of Electromagnetic Analysis and Applications,08,79-94. doi: 10.4236/jemaa.2016.84009
References
- 1. Harrington (1961) Time Harmonic Electromagnetic Fields. Mac Graw Hill.
- 2. Kunz, K. and Luebber, R. (1993) The Finite Difference Time Domain Method for Electromagnetics. CRC, Boca Raton.
- 3. Cherry, P.C. and Iscander, M.F. (1995) FDTD Analysis of High Frequency Electronic Interconnection Effects. IEEE Transactions on Microwave Theory Tech, 43, 2445-2451.
http://dx.doi.org/10.1109/22.466178 - 4. Ferrari, R.L. and Naidu, R.L. (1990) Finite-Element Modeling of High-Frequency Electromagnetic Problems with Material Discontinuities. IEEE Proc, 137, 313-320.
- 5. Lee, J.F. and Sacks, Z. (1994) WETD—A Finite Elements Time Domain Approach for Solving Maxwell’s Equations. IEEE Microwave Guided Wave Letters, 4, 11-13.
http://dx.doi.org/10.1109/75.267679 - 6. Hamdi, N., Aguili, T., Bouallegue, A. and Baudrand, H. (1998) A New Technique for the Analysis of Discontinuities in Microwave Planar Circuits. Progress in Electromagnetic Research, PIER, 21, 137-151.
http://dx.doi.org/10.2528/PIER98051101 - 7. Aguili, T. (2000) Modélisation des composants S. H. F planairespar la méthode des circuits équivalentsgénéralisés. Ph.D. Thesis, National Engineering School of Tunis ENIT.
- 8. Harrington, R.F. (1983) Field Computation by Moment Methods. MacMillan, New York.
- 9. Ooms, S. and De Zutter, D. (1998) A New Iterative Diakoptics-Based Multilevel Moments Method for Planar Circuits. IEEE Transactions on Microwave Theory and Techniques, 46, 288-291.
http://dx.doi.org/10.1109/22.661716 - 10. Aguili, T., Graya, K., Boualegue, A. and Baudrand, H. (1996) Application of a Source Method for Modeling Step Discontinuities in Microstrip Circuit. IEE Proceedings—Microwaves, Antennas and Propagation, 143, 169-173.
http://dx.doi.org/10.1049/ip-map:19960224 - 11. Hamdi, N., Aguli, T. and Boualegue, A. (1998) Considération des sources dans la caractérisation des discontinuities dans les guides d’ondescoplanaires. 6ème colloque Maghrébinsur les Modèles Numériques de l’iIngénieur, Tunis, 24-26 November 1998.
- 12. Hamdi, N., Aguili, T. and Boualegue, A. (1998) Caractérisation des discontinuitésdans les circuits planaires micro-ondes avec une nouvelle technique intégrale. Mediterranean Conference on Electronics and Automatic Control, Marrakech Maroc, 17-19 September 1998.
- 13. Hamdi, N. (1999) Analyse des Discontinuitésdans les circuits planaires par une Nouvelle Formulation de la méthode des Sources. PhD Thesis, National Engineering School of Tunis, ENIT, Tunis.
- 14. El Gouzi, M.E.A. and Boussouis, M. (2010) Hybrid Method for Analyse Discontinuities in Shielded Microstrip. International Journal of Engineering Science and Technology, 2, 3326-3334.
- 15. Pujol, S., Baudrand, H. and Hanna, F. (1993) A Complete Description of a Source Type Method for Modelling Planar Structures. Annals of Telecommunications, 48, 459-470.
- 16. Graya, K., Aguili, T., Boualegue, A. and Boudrand, H. (1999) Characterization of Planar Passive Circuits Using Source Method in Conjunction with Three Different Sets of Trial Functions. IEE Proceeding-Microwaves, Antennas and Propagation, 146, 209-213.
http://dx.doi.org/10.1049/ip-map:19990628 - 17. Graya, K., Aguili, T. and Boualegue, A. (1998) Characterization of Planar Passive Circuits Using Source Method. International Conference on Microelectronics, ICN’98, Monastir, 14-16 December 1998, 131-134.
http://dx.doi.org/10.1109/icm.1998.825586 - 18. Graya, K., Aguili, T. and Boualegue, A. (1999) Etude de discontinuitésplanaires en microruban par uneméthode de source avec différents types d’excitations, Journéessur les télécommunications, Tunisia, 29-31 January 1999.
- 19. Golio, M. and Golio, J. (2007) RF and Microwave Passive and Active Technologies. RF and Microwave Handbook, Second Edition, CRC Press, Boca Raton.
http://dx.doi.org/10.1201/9781420006728 - 20. Hitendra, K., Malik, A. and Singh, K. (2009) Engineering Physics.
- 21. El Gouzi (2015) Modélisation des discontinuitesuni-axialesdans les circuits planairespar la méthode des moments. PhD Thesis, Université Abdelmalek Essaadi, Tétouan.
- 22. Ourabia, M. (2014) Modelling and Characterization of Planar Components. Advanced Materials Research, 1025-1026, 1055-1061.
http://dx.doi.org/10.4028/www.scientific.net/amr.1025-1026.1055 - 23. Lea, D. (1997) Concurrent Programming in Java. Addison Wesley Pub., Boston.
- 24. Weems, C.C., Weaver, G.E. and Dropsho, S.G. (1994) Linguistic Support for Heterogeneous Parallel Processing: A Survey and an Approach. Proceedings of the Heterogeneous Computing Workshop, Cancun, 26 April 1994, 81-88.
- 25. Weems, C. (1998) Heterogeneous Programming with Java: Gourmet Blend or Just a Hill of Beans? Proceedings of the 7th Heterogeneous Computing Workshop, Orlando, 30 March 1998, 173-182.
- 26. Salah, T.B. (2009) Etude des structures invariantes par échelles par uneméthodeintégrale multi modalecombinée à la méthode de normalization. PhD Thesis, National Engineering School of Tunis, ENIT, Tunis.
- 27. Oueslati, B., Salah, T.B., Chiraz, L. and Aguili, T. (2016) Rigorous Study of a Microstrip Line Excited with Perpendicular Coaxial Source Using MGEC MoM Based Method. 3rd International Conference on Automation, Control Engineering and Computer Science, ACECS-2016, Hammamet, 20-22 March 2016.






















