Journal of Electromagnetic Analysis and Applications
Vol.08 No.01(2016), Article ID:63209,14 pages
10.4236/jemaa.2016.81002
Antenna Performance Improvement in Elliptical Array Using RMI Method of Mutual Coupling Compensation
Aluru Venkata Lakshmi Narayana Rao1, Nunna Bala Ankaiah2, Dharma Raj Cheruku3
1Department of ECE, SSNCET, Ongole, India,
2ECIL, Hyderabad, India,
3Departement of ECE, GIT, GITAM University, Visakhapatnam, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 December 2015; accepted 25 January 2016; published 29 January 2016
ABSTRACT
The number of wireless electronic gadgets used in mobile communication, vehicle collision avoidance system, compact radars, etc. is extremely increasing at a rapid rate. Thus, the characteristics of the antennas involved in these gadgets are to be designed very stringently so as to avoid interferences & coupling and to improve compatibility, susceptibility, etc. Compact smart antenna with improved performance is highly essential to meet this challenging scenario. Mutual coupling between various elements of an array is one of the main factors which can be considered for improvement of performance of the antenna. Influence of mutual coupling on performance of the antenna is considered in this paper and various techniques to minimize this effect are presented. Effect of mutual coupling on radiation characteristics of the antenna can be compensated employing various methods like Conventional Mutual Impedance (CMI), Receiving Mutual Impedance (RMI). Analysis is presented as comparison between the two methods for different number of elements in the array. Analysis is also presented for different geometries of the array like circular and elliptical for improved performance. The results show performance improvement in the proposed array for parameters like SNR and Speed of convergence.
Keywords:
Antenna Arrays, Elliptical (Oval) Arrays, Mutual Coupling, Compensation Methods, Beam Forming

1. Introduction
Wide spread application of wireless communication technology in daily life demands efficient and reliable signal transmission. Increased directivity, user capacity, battery life and source separation can be achieved by smart antenna to cope-up the demands. Smart antenna is popularly used in radar systems, wireless communications and in vehicle collision avoidance applications [1] . Antenna array is an integral part of smart antenna system. In smart antenna system, array of elements are designed to achieve required beam form for a given application.
A systematic arrangement of group of radiating elements is called an array. Size of the array and aperture proportionally increases with gain of the antenna [2] . Two methods to increase the aperture size of the array are to increase the number of elements and/or inter element spacing of the array [3] . Computational complexity increases with the number of elements. However, this leads to increase in grating lobes. Power efficiency reduces due to grating lobes [4] . A compromise between these two parameters can be achieved by reorienting the geometry and number of elements in the array.
Linear array is simple in structure and is limited to estimation of the elevation angle (one dimensional) of incoming signal only. In addition, the linear array can only estimate the range of azimuth angle limited by 180˚ (−90˚ < θ < 90˚) [5] . Hence the accuracy of Direction of Arrival (DOA) estimation is greatly affected when the incoming signal is within the range of end-fire array (70˚ < |θ| < 90˚).
The entire transmitted signal is equal to the sum and reradiated signal from the elements. Similarly, induced current on the antenna element reradiates electromagnetic field which would be received by the other neighboring elements in the array. Such mutual coupling effect is usually considered as a defect which degrades the performance of the array. Two types of coupling compensation methods: Conventional Mutual Impedance (CMI) and Receiving Mutual Impedance (RMI) methods are popular.
2. The Mutual Coupling Analysis
For an antenna array with N elements, receiving an incoming signal, being a plane wave source, the received terminal voltage at the kth antenna element Vk can be expressed as
 (1)
(1)
Uk = received voltage of kth antenna element by the plane wave source alone
Wk = coupled voltage of the scattered fields from the other antenna elements in the array
The coupled voltage Wk in (1) can be written as [6] -[8]
 (2)
(2)
where Zk is the receiving mutual impedance between the kth and the ith antenna elements and Ii is the terminal current at the ith antenna element given by:
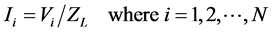
with ZL being the terminal load impedance of the antenna elements. Putting (2) and (3) into (1), we have:
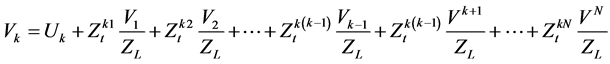 (3)
(3)
The relationship between the uncoupled voltages Uk and the received voltages (i.e., coupled voltages) Vk can be written in a matrix equation as:
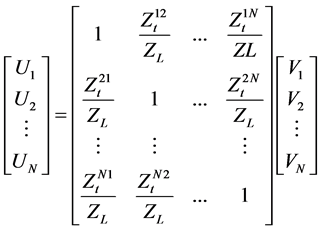 (4)
(4)
2.1. Conventional Mutual Impedance Method
A circuit theory approach for reducing or compensating mutual coupling effect is discussed in this work. This method is called conventional mutual impedance method (CMI) [9] . Common mutual coupling can be easily measured directly or from S-parameters.
The relation between the terminal voltage and current can be given by
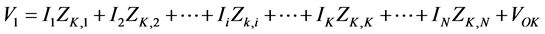 (5)
(5)
ZL being impedance, relation between voltage and current is given by
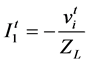 (6)
(6)
The relationship between the open-circuit voltages and terminal voltages can be written as
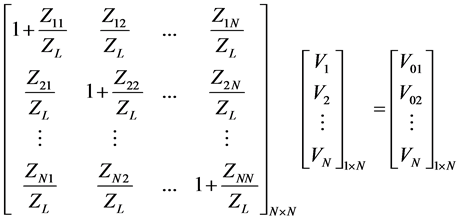 (7)
(7)
2.2. The Receiving Mutual Impedance
Another circuit theory approach for reducing or compensating mutual coupling effect is receiving mutual impedance method (RMI) [10] . The concept of receiving mutual impedance was suggested [11] as an alternative to the concept of conventional mutual impedance [12] . In fact, the need to handle mutual coupling problems differently in transmitting and receiving arrays has been noted before in mobile communications [13] and [14] . The basic difference between the receiving mutual impedance and the conventional mutual impedance lies in the fundamental causes of the coupling. In the conventional mutual impedance, the coupling is caused by the transmitting current distribution on an antenna while in the receiving mutual impedance; the coupling is caused by the receiving current distribution on an antenna.
The receiving mutual impedance between two antennas is the ratio of the coupled voltage across antenna1’s terminal load ZL1 (due to the receiving current distribution on antenna 2) to the terminal current through antenna 2’sterminal load ZL2 when the array is excited by an external plane wave source.
 (8)
(8)
i.e. Receiving mutual impedance with a receiving current on antenna 2 = coupled voltages across antenna 1’s terminal load/receiving current through antenna 2’s terminal load.
The definition of the receiving mutual impedance requires specifying a plane wave to excite the two antennas as shown in Figure 1. The coming direction of the plane wave is to be the same as the direction of the signal that the array is designed. In Figure 1, V1 and V2 are the received voltages across the terminal loads of antennas 1 and 2, respectively. The corresponding currents through the two antennas are I1 and I2. In equation (1), U1 is the received voltage across the terminal load of antennas 1 when antenna 1 is excited by the external plane wave source alone (with antenna 2 removed from the array). U1 is also called the isolation voltage on antenna 1.
3. Geometry and Array Factor
Two different geometries of the array are considered for comparison in this paper viz., Circular and Elliptical (Oval).
3.1. Circular Array
In circular array it is assumed that N equally spaced isotropic elements are placed on X-Y plane along a circular ring. Let the radius be “a”. Circular array can able to scan 360˚ azimuthally. The geometry of N-element circular
Figure 1. Mutual impedance between antennas.
array antenna is shown in Figure 2 [15] . The array factor is given by the equation [16]
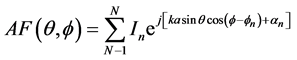 (9)
(9)
where,
In = amplitude of excitation
αn = phase of the n th element
θ = elevation angle from z axis.
Circumference = 2πr
Area = πr2
The radius of the array increases the directivity of uniform circular array and tends to a value N [17] .
3.2. Elliptical Antenna Array
The geometry of the elliptical antenna array with origin as center is shown in Figure 3 [18]
The array factor is given by equation (10) [19] .
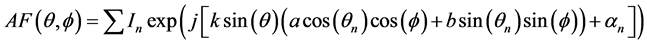 (10)
(10)
In=amplitude of excitation
αn=phase of the n th element
θ=elevation angle from z axis.
øn=Azimuth angle measured from x axis for n-th element.
a, b=semi major and minor axises respectively.
e=eccentricity of elliptical array and is 0.5
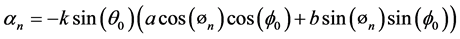 (11)
(11)
θ0 = 90˚, ø0 = 0˚.
N=no of elements is 8 or 10.

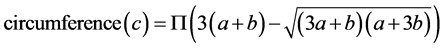
Comparisons of area of circular and elliptical arrays are given below in Table 1.
4. Results
4.1. Conventional Mutual Impedance Method of Compensation
The objective is to analyze the response of elliptical antenna array with modified LMS (Least Mean Square) algorithm which optimizes the weight factor for DOA (Direction of Arrival) estimation. Mutual coupling is minimized by the CMI method in this case.
Example 1: Eight (Dipole) Element Array using CMI
In this example, an 8-element array using CMI is optimized with uniform spacing between the elements. It is assumed that the angle of signal and interference be 90˚ and 180˚ respectively.
Figure 2. Geometry of circular antenna in XY-plane.
Figure 3. Geometry of ellipse in XY-plane.
Table 1. Comparision of area of circular and ellptical arrays.
It can be evident from Figure 4 and Figure 5, that elliptical (oval) array with CMI method has reduced number of side lobes. Also, lower response of −20 dB observed in the interference direction, compared to circular antenna with −10 dB response.
Figure 6 and Figure 7 compare the output noise in circular and elliptical antennas. Elliptical antenna has noise power which is less by 0.5 dB (negligible noise) for the iterations 10 to 100, whereas the circular antenna has considerable noise at low iteration rates below 20 for minimum of 0.5 dB. Hence it can be concluded that convergence is fast in elliptical array antenna than in circular for low noise.
Example 2: Ten (Dipole) Element Array using CMI
In this example, a 10-element array using CMI is optimized with uniform spacing between the elements. It is assumed that the angle of signal and interference be 90˚ and 180˚ respectively.
In Figure 8, iterations vs. SNR in circular array with 10-elements (uniform spacing between elements) using RMI Method is presented. Figure 9 is similar plot for Elliptical array. The elliptical antenna leads with better SNR than circular antenna for iterations below 20. Circular antenna has −10 dB SNR and elliptical antenna has −2 dB which confirms the faster convergence of elliptical array.
Figure 10 shows circular array with CMI Method and without CMI Method which has deeper nulls if compensation is not applied. But elliptical array performance is good with null points covered by peaks as shown in Figure 11.
Figure 4. Circular array using CMI Method.
Figure 5. Elliptical (oval) array with CMI Method.
Figure 6. Iterations vs. output noise in circular array with CMIMethod.
In CMI compensation both 8 & 10 element arrays of circular and elliptical arrays are compared. Elliptical arrays show better in pattern generation, SNR and convergence speed. Advantage of elliptical antenna compared to circular antenna is its low area for same number of elements.
Figure 7. Iterations vs. output noise in Elliptical(oval) array using CMI Method.
Figure 8. Iterations vs. SNR in circular array with CMI Method.
Figure 9. Iterations vs. output SNR in Elliptical array using CMI Method.
Figure 10. Circular array with and without CMI Method.
Figure 11. Elliptical array with and without CMI Method.
4.2. The Receiving Mutual Impedance Method of Compensation
In this RMI Method, the source and noise are assumed to be 90˚ and 180˚ of azimuth directions respectively. A modified LMS algorithm is used to optimize the weight factor for DOA estimation.
Example 3: Eight (Dipole) Element Array using RMI
In this example, an 8-element Circular array is optimized with uniform spacing between the elements.
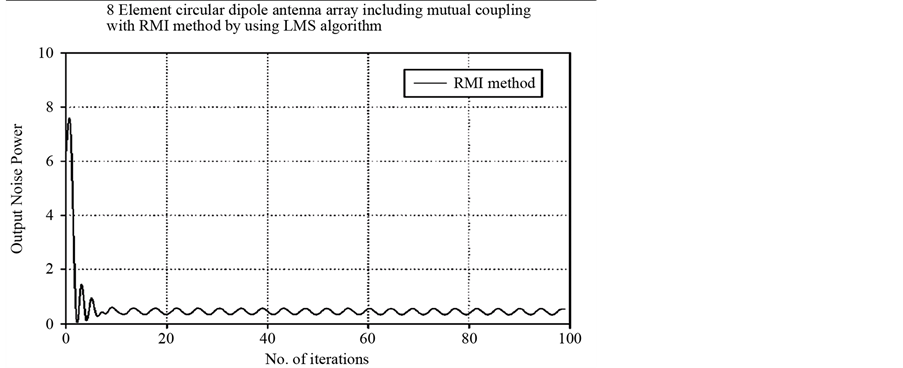
The best amplitude value determined by the optimized technique is shown in Figure 12. From Figure 13 it can be noted that the output noise power sustains minimum with the number of iterations above 10.
It can be evident that from Figure 13 elliptical array with RMI Method has reduced side lobes and peaks compared with circular array with RMI Method in Figure 12. Elliptical antenna has lower response in the interference direction than circular antenna.
Figure 14 and Figure 15 compare the output noise in circular and elliptical arrays. Elliptical antenna has negligible noise throughout the iterations from 10 to 100 below 0.5 dB, whereas the circular antenna has noise slightly more than that of elliptical antenna. Also below 10 iterations makes much difference in both antenna output noise. Convergence is faster in elliptical antenna.
Example 4: Ten (Dipole) Element Array using RMI
In this example, a 10-element array with uniform spacing between the elements is optimized using RMI. As per the Figure 16 & Figure 17 for Iterations vs. SNR in circular and elliptical arrays (no of elements 10) using
Figure 12. Circular array with RMI Method.
Figure 13. Elliptical (oval) array with RMI Method.
Figure 14. Iterations vs. output noise in circular array with RMI Method.
Figure 15. Iterations vs output noise in Elliptical (oval) array using RMI Method.
Figure 16. Iterations vs. SNR in circular array with RMI Method.
Figure 17. Iterations vs. output SNR in Elliptical array using RMI Method.
RMI Method, the elliptical antenna has better SNR below 20 iterations. Hence convergence is faster in elliptical antenna. For the iterations below 10, circular array has minimum of −12 db SNR.
Figure 18 and Figure 19 presents the comparison between the patterns generated with RMI and without RMI method for circular array and elliptical antennas. Elliptical antenna beam minimized lobe in 120˚ to 240˚, azimuth angle compared to circular antenna.
Example 5: Sixteen (Dipole) Element Array using RMI
In this example, an 16-element Circular & Elliptical arrays are optimized with uniform spacing between the elements. Simulations are shown in Figure 20 & Figure 21. It observed that from Figure 21 Elliptical (oval) array with RMI Method has reduced side lobes and peaks compared with circular array. Elliptical antenna has peak at −28 dB in the interference direction as circular antenna has −21 dB
In RMI compensation along with 8 & 10 element arrays of circular and elliptical arrays, 16-element arrays are also compared. Elliptical arrays shows better in pattern generation, SNR. Convergence speed is more improved. Geometrical advantage of compact size for elliptical antenna with same number of elements as in circular antenna is sustained.
More over RMI sanctions receiving current distribution on an antenna compared to CMI mode of compensation. It is additional advantage to recommend the RMI in elliptical arrays so that DOA estimation depends on Direction of receiving signal strength.
Example 6: Sixteen (Dipole) Element Array with non linear spacing using RMI
Figure 22 and Figure 23 compares the output of 16-element circular & elliptical antenna with non linear spacing. Elliptical antenna has lower response at 210˚, 270˚ and 330˚ Azimuth direction, whereas the circular antenna has response better than that of elliptical antenna. Also, side lobes are more in circular antenna.
Lobes between 180˚ - 240˚ & 300˚ - 330˚ are smoothening and shaped compared to circular array in elliptical antenna.
However, below 180˚ of angle uniform spaced array is seems to be performing better.
5. Conclusions
The simulations categorically show that CMI compensation method applied to elliptical array with 8 & 10 elements has better response in pattern generation, convergence speed and SNR compared with circular array. Compactness of elliptical antenna compared to circular antenna for the same number of elements is additional geometrical advantage.
Using RMI compensation method, a comparison is made for 8, 10 and 16 element array in circular as well as elliptical array. Elliptical arrays show better performance in pattern generation, SNR. Convergence speed is better compared to CMI method of compensation. Moreover, receiving current distribution on an antenna for RMI
Figure 18. Circular array with and without RMI Method.
Figure 19. Elliptical array with and without RMI Method.
Figure 20. 16-Element Circular Dipole Antenna array with signal and inter- ference at 90˚and 180˚.
Figure 21. 16-Element elliptical (oval) Dipole Antenna array with signal and interference at 90˚ and 180˚.
Figure 22. 16-Element Circular Dipole Antenna array with non-uniform signal and interference at 90˚ and 180˚.
Figure 23. 16-Element Elliptical (oval) Dipole Antenna array with non-uniform signal and interference at 90˚ and 180˚.
method is better compared to CMI mode of compensation. It is additional advantage to recommend the RMI in elliptical arrays because DOA estimation depends on Direction of receiving signal strength.
Also, the simulation of non uniform spaced elements array in either circular or elliptical patterns confirms that below 180 degrees of angle, uniform spaced array performance is better. Hence, it can be concluded that elliptical array of uniform spaced elements with RMI compensation method of mutual coupling has the best performance in a smart antenna.
Cite this paper
Aluru Venkata Lakshmi NarayanaRao,Nunna BalaAnkaiah,Dharma RajCheruku, (2016) Antenna Performance Improvement in Elliptical Array Using RMI Method of Mutual Coupling Compensation. Journal of Electromagnetic Analysis and Applications,08,8-21. doi: 10.4236/jemaa.2016.81002
References
- 1. Okamoto, G.T. (2002) Smart Antenna Systems and Wireless LANs. Kluwer Academic, Santa Clara.
- 2. Haupt, R.L. (2010) Antenna Arrays: A Computational Approach. John Wiley and Sons, Hoboken, New Jersey.
http://dx.doi.org/10.1002/9780470937464 - 3. Fenn, A.J. (2008) Adaptive Antennas and Phased Arrays for Radar and Communications. Artech House Publishers, Massachusetts Institute of Technology, Norwood, MA.
- 4. Balanis, C.A. (2008) Modern Antenna Handbook. John Wiley and Sons, Hoboken, New Jersey, 135.
http://dx.doi.org/10.1002/9780470294154 - 5. Ioannidis, P. and Balanis, C.A. (2005) Uniform Circular Arrays for Smart Antennas. IEEE Antennas and Propagation Magazine, 47, 192-206.
http://dx.doi.org/10.1109/MAP.2005.1589932 - 6. Arrival Estimation for Antenna Arrays. Morgan & Claypool, Arizona State University, Tempe, AZ.
- 7. Lui, H.-S. Hui, H. T. and Leong, M. S. (2008) Investigation of Direction-of-Arrival Estimation Using Uniform Linear Arrays with Different Antenna Separations and Array Apertures. Presented at the Asia Pacific Microwave Conference.
- 8. Balanis, C.A. (1997) Antenna Theory: Analysis and Design. Wiley, New York.
- 9. Collin, R.E. and Zucker, F.J., Eds. (1968) Antenna Theory. McGraw-Hill, New York.
- 10. Balanis, C.A. and Ioannides, P.I. (2007) Introduction to Smart Antenna. Morgan and Claypool, Arizona.
- 11. Singh, H., Sneha, H.L. and Jha, R.M. (2013) Mutual Coupling in Phased Arrays: A Review. International Journal of Antennas and Propagation, 2013, Article ID: 348123.
- 12. Hopkins, G.D., Ratner, J., Traille, A. and Tripp V. (2007) Aperture Efficiency of Amplitude, Weighting Distributions for Array Antennas. 2007 IEEE Aerospace Conference, Big Sky, 3-10 March 2007, 1-9.
http://dx.doi.org/10.1109/aero.2007.352856 - 13. Cao, W.Q., Xiang, Y., Zhang, B.N., Liu, A.J., Yu, T.B. and Guo, D.S. (2011) A Low-Cost Compact Patch Antenna with Beam Steering Based on CSRR Loaded Ground. IEEE Antennas and Wireless Propagation Letters, 10, 1520-1523.
http://dx.doi.org/10.1109/LAWP.2011.2181316 - 14. Chan, S.C. and Chen, H.H. (2006) Uniform Concentric Circular Arrays with Frequency Invariant Characteristics— Theory, Design, Adaptive Beam Forming and DOA Estimation. IEEE Transactions on Signal Processing, January 2007, 165-177.
- 15. Tvrdik, J., Pavliska, V. and Habiballa, H (2008) Stochastic Self-Adaptive Algorithms for Global Optimization— MATLAB and C++ Library.
http://www1.osu.cz/home/habibal/optimization/index.html - 16. Ammula, V., Rao, S.M. and Wentworth, S.M. (2010) Dual Excited Planar Circular Array Antennas for Direction Agile Applications. 42nd Southeastern Symposium on System Theory, Tyler, 7-9 March 2010, 138-142.
http://dx.doi.org/10.1109/ssst.2010.5442853 - 17. Ahmidi, N., Neyestanak, A. and Dawes, R. (2008) Elliptical Array Antenna Design Based on Particle Swarm Method Using Fuzzy Decision Rules. 24th Biennial Symposium on Communications, Kingston, 24-26 June 2008, 352-355.
http://dx.doi.org/10.1109/BSC.2008.4563274 - 18. Chou, J.Y.-L. (2002) An Investigation on the Impact of Antenna Array Geometry on Beam Forming User Capacity. Master of Science (Engineering), Queen’s University, Kingston.
- 19. Ioannidis, P. and Balanis, C.A. (2005) Uniform Circular Arrays for Smart Antennas. IEEE Antennas and Propagation Magazine, 47, 192-206.
http://dx.doi.org/10.1109/MAP.2005.1589932