Journal of Electromagnetic Analysis and Applications
Vol.07 No.10(2015), Article ID:60462,5 pages
10.4236/jemaa.2015.710027
Comparison of Excitation of Acoustic-Electromagnetic Wave in Piezoelecric Crystal and Crystal with Potential of Deformation
S. Koshevaya, V. Grimalsky, Y. Kotsarenko, J. Escobedo-Alatorre
Autonomous University of Morelos State, CIICAp, Cuernavaca, Mexico
Email: svetlana@uaem.mx
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2015; accepted 19 October 2015; published 22 October 2015
ABSTRACT
In this article, the comparison of excitation in high frequencies of acoustic-electromagnetic wave in piezoelecric crystal and crystal with potential of deformation GaAs is investigating. Possible mechanisms of coupling different hybrid waves are the piezoeffect and the deformation potential. As a model it is analyzing a film of crystal places between two symmetrical substrates with the other materials without an acoustic contact. This film includes 2D electron gas with a high negative differential conductivity and uniform initial distribution of electrons. The hybrid acoustic-electromagnetic wave and hybrid space charge wave interact. Amplification of space charge wave takes place due to negative differential conductivity in GaAs. This amplification of space charge waves is causing the amplification of acoustic-electromagnetic wave. It is to show that the symmetric modes, emerging as transverse ones, interact more effectively with the space charge waves. Another important result is the following: at the frequencies f ≈ 10 GHz, the excitation efficiency of acoustic-electromagnetic wave with transverse displacement due to piezoeffect is more effective, but at higher frequencies, the deformation potential is dominating.
Keywords:
Piezoelectric Crystal, Deformation Potential, Acoustic-Electromagnetic and Space Charge Waves

1. Introduction
The amplification of the acoustic-electromagnetic waves is very important problem [1] . A possible solution of this problem is the resonant coupling of acoustic waves with the microwave electric field of space charge waves (SCW) in materials possessing negative differential conductivity (NDC) like GaAs [2] [3] . Namely, under pro- pagation in the bias electric field higher than the critical value for observing negative differential conductivity (NDC), the SCW is subject to amplification, and its microwave electric field can achieve high values. Due to piezoeffect or deformation potential, this microwave electric field excites hypersonic acoustic-electromagnetic waves (AEW). In [2] [3] , it is demonstrated that this excitation has a resonant character with respect to the frequency and the thickness of the GaAs film. The critical value of bias electric field in GaAs is Ec = 3.5 kV/cm that it is good for analysis of amplification in different mechanisms like piezoeffect or deformation potential so as other materials have very big critical field like crystal InP and GaN.
The present paper is focused on theoretical research of excitation of acoustic-electromagnetic waves (AEW) in GaAs films of a sub-micron thickness placed between non-piezoelectric substrates. The spatial increments of SCW due to NDC have been calculated for two mechanisms like piezoeffect and deformation potential. An amplification of SCW is possible for frequencies from 10 GHz for case of piezoeffect. For deformation potential the frequencies range increase from 10 GHz to 30 GHz, so the mechanism of deformation potential is more useful in high frequencies.
The thin GaAs film plays the role in a transducer of acoustic electromagnetic waves. The amplification has a resonant character, and the intensities of energy may reach the values of 10 W/cm2. The realization of the good amplification has showed that usefulness of hybrid waves in high frequencies range more f ≈ 10 GHz is very important for application in communication, medicine and control systems. The analysis of basic mechanisms of amplification is given in this article. The resonance excitation and amplification of acoustic-electromagnetic wave with space mode in structure of GaAs is analyzing for two cases of piezoeffect and deformation potential, but the amplification of high frequencies are realizing only in case of deformation potential.
2. Model of Amplification Due to Piezoeffect
Let us to consider a thin film of n-GaAs located between two mediums, the substrates are from material without piezoeffect, and the transversal wave passed along z axis. The component of displacement U is in direction of the y axis. The film consists of a 2D gas with a high negative differential mobility. The value L is the length of the element (along axis OZ), h is the thickness of film (see Figure 1). This film has a substrates with depth d. The hybrid wave is decreasing in the substrate, then, all its energy is in the very thin film with 2D electron beam. The effective size of the waveguide is describing by the parameter 2H = 2(h + d/2), d is the depth of substrate.
Let us to analyze the simplest transversal in displacements u mode using elastic theory equation with the pie-
zoeffect [1] . It is necessary to use the variable electric field 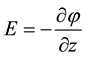 (in direction of axes Z) determined by
(in direction of axes Z) determined by
potential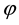 ,
,
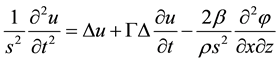 1(a)
1(a)
Figure 1. Geometry of waveguide for computing simulation of amplification acoustic-electromagnetic wave where 2 h is the transversal size of guide in x direction and L is the length of the guide. In direction y the model of guide has size going to infinitive value.
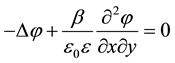 1(b)
1(b)
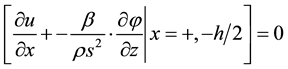 , 1(c)
, 1(c)
where s » 3 × 105 cm/s is the sound velocity,  is the module of coefficient of piezoeffect,
is the module of coefficient of piezoeffect, 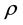 is the density parameter,
is the density parameter, 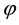 is the potential determined the electric field
is the potential determined the electric field 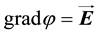 [1] -[5] .
[1] -[5] .
The boundary conditions are in (Equation 1(c)). In the case of free very thin film it is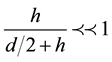 . In this
. In this
case it is necessary to consider the viscosity coefficient  for the simulation. The wave process shows that the amplification realizes if the synchronism between the acoustic-electromagnetic wave with transversal displacement mode and the space charge wave [5] ,
for the simulation. The wave process shows that the amplification realizes if the synchronism between the acoustic-electromagnetic wave with transversal displacement mode and the space charge wave [5] ,
 (2)
(2)
where 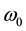 is the frequency of synchronism, s,
is the frequency of synchronism, s,  is sound and space charges waves velocities, respectively; index
is sound and space charges waves velocities, respectively; index ), H must have also an optimal value.
), H must have also an optimal value.
Resonance condition 
where

Parameters 
and

These conditions for the amplification are better for the symmetric modes if the displacement

Boundary conditions are taken in case of the absent of the acoustic contact of the film with the environment (Equation 1(c)).
In the simulation it is to use Equation (1) and the resonance condition (2). It is necessary to take into account the 2D electron gas of n-GaAs thin film and the equations for slow changing amplitudes of acoustic-electro- magnetic hybrid wave with potential
Traditional construction for realization of acoustic-electromagnetic amplification is in Figure 3. This construction is for high frequencies f » 1011 Hz ranges too.
Additionally, in simulations it is considering the electric variable field distribution in input antenna like Gauss impulse.
Figure 2. Distribution of the amplitude of acoustic deformation 
Figure 3. Traditional structure for exiting of acoustic-electromagnetic waves. It is necessary to prepare the cathode and anode 1, and the input 3 and the output 4 antennas; the film of n-GaAs is in i-GaAs substrate.
Figure 4. Distribution of the displacements deformation amplitude along the film in direction z at time t = 4 ns with a size of wave guide H = 0.1 μm.
Electric variable field distribution in input antenna has parameters: z1 = 0.001 cm, z0 = 0.0001 cm; y1 = 0.05 cm, y0 = 0.02 cm; t1 = 2.5 ns, t0 = 1.25 ns; E10 = 200 V/cm and EB = 4.56 kV/cm, the drift field, n0 = 1011 cm−2, the 2D concentration of electron gas, and q, the transverse wave number (index m equal 5) of the acoustic-electro- magnetic mode.
Excitation of the acoustic-electromagnetic wave due to deformation potential is in the Lamb’s acoustic mode [1] , which possess longitudinal component of mechanic displacement, has the electric field too and interacts with space charge waves due to the deformation potential. The equation for the elastic displacement components of the Lamb’s wave [1] u = (u1, 0, u3) takes a form.

Here 

As in the case of piezoactive transverse modes, the effective excitation of acoustic-electromagnetic waves with displacement like in Equations (3) takes place near cut-off frequency. It is shown that the symmetric modes emerging as transverse ones interact more effectively with the space charge waves. A distribution of the displacements near cut-off is

here sl » 5.5 × 105 cm/s is the longitudinal sound velocity in GaAs [7] .
The computer modeling in the base of Equations (3) and (4) is the same like for case the piezoeffect. This modeling has demonstrated that the distributions in the plane of the film of excited acoustic-electromagnetic waves are very similar to those obtained for piezoeffect. But it is shown ¡ that the efficiency of excitation due to deformation potential becomes dominating at higher frequencies f > 30 GHz.
3. Conclusion
The resonant interaction of space charge waves with acoustic-electromagnetic waves in thin GaAs films can be used for effective in microwave wave range. At the frequencies f < 30 GHz efficiency of excitation of acoustic- electromagnetic due to piezoeffect is more effective, but at higher frequencies, deformation potential is dominating. An intensity of acoustic-electromagnetic waves can reach 10 W/cm2 at microwave frequencies range f = 10 GHz ÷ 30 GHz. To increase a frequency of excited wave to millimeter range, it is possible to choose the resonant excitation of acoustic-electromagnetic waves at the second harmonic of the input signal.
Acknowledgements
Authors thank SEP-CONACyT for the support of our work.
Cite this paper
S.Koshevaya,V.Grimalsky,Y.Kotsarenko,J.Escobedo-Alatorre, (2015) Comparison of Excitation of Acoustic-Electromagnetic Wave in Piezoelecric Crystal and Crystal with Potential of Deformation. Journal of Electromagnetic Analysis and Applications,07,259-264. doi: 10.4236/jemaa.2015.710027
References
- 1. Dieulesaint, E. and Royer, D. (2000) Elastic Waves in Solids. Springer, New York.
- 2. Grimalsky, V., Gutierrez-D., E., Garcia-B., A. and Koshevaya, S. (2004) Resonant Excitation of Microwave Acoustic Modes in n-GaAs Film. Proceedings of International. Conference on Microelectronics ICM-2004, Tunis, 6-8 December 2004, 72-75.
http://dx.doi.org/10.1109/icm.2004.1434209 - 3. Grimalsky, V., Gutierrez-D., E., Garcia-B., A. and Koshevaya, S. (2006) Resonant Excitation of Microwave Acoustic Modes in n-GaAs. Microelectronics Journal, 37, 395-403.
http://dx.doi.org/10.1016/j.mejo.2005.06.003 - 4. Mitin, V.V., Kochelap, V.A. and Stroscio, A. (1999) Quantum Heterostructures: Microelectronics and Optoelectronics. Cambridge University Press, Cambridge.
- 5. Shur, M. (1989) GaAs Devices and Circuits. Plenum Press, New York.
- 6. Carnez, B. (1980) Modeling of Submicrometer Gate FET Including Effect of Nonstationary Dynamics. Journal of Applied Physics, 51, 784-790.
- 7. Koshevaya, S.V., Grimalsky, V.V., Garcia-B., A. and Díaz-A., M.F. (2006) Amplification of Hypersonic by GaAs Crystals. Ukrainian Journal of Physics, 51, 594-598.







