Received 28 May 2014; revised 26 June 2014; accepted 23 July 2014

ABSTRACT

The quasi-steady electromagnetophoretic motion of a spherical colloidal particle positioned at the center of a spherical cavity filled with a conducting fluid is analyzed at low Reynolds number. Under uniformly applied electric and magnetic fields, the electric current and magnetic flux density distributions are solved for the particle and fluid phases of arbitrary electric conductivities and magnetic permeabilities. Applying a generalized reciprocal theorem to the Stokes equations modified with the resulted Lorentz force density and considering the contribution of the magnetic Maxwell stress to the force exerted on the particle, which turns out to be important, we obtain a closed-form formula for the migration velocity of the particle valid for an arbitrary value of the particle-to-cavity radius ratio. The particle velocity in general decreases monotonically with an increase in this radius ratio, with an exception for the case of a particle with high electric conductivity and low magnetic permeability relative to the suspending fluid. The asymptotic behaviors of the boundary effect on the electromagnetophoretic force and mobility of the confined particle at small and large radius ratios are discussed.

Keywords:

Electromagnetophoresis, Magnetohydrodynamics, Lorentz Force, Colloid

1. Introduction

An unbounded, electrically conducting, Newtonianfluid under the simultaneous application of an electric current density 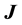and a non-collinear magnetic flux density 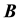will undergo a magnetohydrodynamic flow in the direction perpendicular to both the applied fields. This fluid flow is driven by the resulted Lorentz force density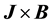, which plays as an additional term in the Navier-Stokes equation [1] -[3] . In an enclosed fluid, this body force is compensated by an established pressure gradient, analogous to the hydrostatic pressure gradient in the gravitational field, and the fluid will be at rest.

When a colloidal particle is freely suspended in a fluid subjected to the Lorentz force,the force acts on both the fluid and the particle. If the force exerted on the particle is different from that on the fluid, then relative migration, known aselectromagnetophoresis (EMP), of the particle occurs in the direction of or against, depending on their relative electromagnetic properties. The effect of EMP is of considerable importance in numerous practical applications, such as the separation of biological particles (DNA fragments, proteins, cells, yeasts, etc.) due to the differences in their sizes and electric conductivities [4] - [8] , aggregation and disaggregation of colloidal suspensions [9] - [11] , removal of small nonmetallic inclusions or impurities from molten metals [12] [13] , measurement of the particle-wall interaction force [14] [15] , determination of glycation on diabetic erythrocytes [16] , operation of multicolor display devices [17] , and manipulation of autocatalytic micro/nano- motors or other colloidal particles [18] - [22] .

The mechanism of EMP was first reported by Kolin [23] [24] who carried out an analysis for a spherical particle of radius 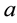in an unbounded fluid of viscosity 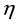with arbitrary electric conductivities and obtained a simple formula for the particle velocity in proportion to the quantity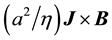. In practical applications of the EMP effect, colloidal particles are not isolated and will move in the proximity of solid boundaries [6] [7] [25] . Therefore, it is of interest to examine the boundary effects on the EMP migration of a particle. Recently, the EMP motions of a spherical particle in the vicinity of a plane wall were investigated using spherical bipolar coordinates [26] and a method of reflections [27] . Asymptotic expansions in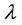, the ratio of the particle radius to the distance of the particle center from the wall, generated by the reflection method indicate that the leading- order wall-induced corrections (retardation effects) to the EMP force and migration velocity of the particle appear at 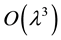and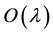, respectively.

In this paper, the EMP motion of a colloidal sphere in a concentric spherical cavity filled with a conducting fluid subject to uniformly prescribed electric and magnetic fields is analyzed with the consideration of the total force (including the Maxwell stress) exerted on the particle, where the particle and fluid may have arbitrary values in electric conductivity and magnetic permeability. Although the concentric cavity is an idealized abstraction of some real systems, the result of boundary effect on the electrophoretic velocity of a charged sphere obtained in this geometry [28] agrees with that for a circular cylindrical pore [29] . The geometric symmetry in this model system allows closed-form formulas for the EMP force and migration velocity of the confined particle to be obtained in Equations (15) and (20), respectively.

2. Analysis

We consider the EMP motion of a spherical colloidal particle of radius 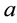situated at the center of a spherical cavity of radius 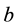filled with a conducting fluid of viscosity 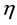subject to an applied electric current field and a perpendicularly applied magnetic induction field 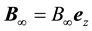at the quasi-steady state and low Reynolds number, as shown in Figure 1, where 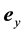and are two principal unit vectors in the rectangular coordinates, and both the electric current density and magnetic flux density are constant. The particle surface and cavity wall are allowed to bear electric charges and the conducting fluid may be an electrolyte solution, but the electric double layersadjacent to the particle and cavity surfaces are assumed to be thin relative to the particle radius and the gap width between the solid surfaces such that the entire fluid phase is electrically neutral with a uniformity in the ionic composition. Electrokinetic (electrophoretic and/or electro-osmotic) and gravitational effects, which have been considered separately [30] - [32] and can be added directly due to the linearity of the problem, are ignored here. The objective is to determine the boundary effect of the enclosing cavity on the EMP velocity of the particle.

2.1. Electric Potential Distribution

The electric conductivities of the particle and of the fluid are taken as constants. Thus, the electric potential distributions are governed by the Laplace equations

(1a)

for the particle and

(1b)

for the fluid, where are spherical coordinates.

The boundary conditions for the potential distributions and at the particle surface and cavity wall are

(2a)

; (2b)

, (3)

where the electric current density distributions in the particle and fluid phases are

(4a,b)

respectively, and is the unit vector in the direction. Equations (2a) and (2b) stand for the continuity of the normal component of the current density and the tangential component of the electric field at the particle surface, respectively, and Equation (3) gives the uniformly applied current density in the fluid phase in the absence of the particle. The additional electric current induced by the fluid motion under the applied magnetic field is negligible relative to the applied electric current (the typical value of their ratio or the Hartmann number square is about) [22] .

The solution to the above equations is

, (5a)

, (5b)

where

, (6)

is a surface harmonic, , , and. The constant terms in Equation (5) are trivial and have been omitted.

2.2. Magnetic Flux Density Distributions

The magnetic permeabilities of the particle and of the fluid are also taken to be constants, and the magnetic flux density distributions are governed by [1]

(7a,b)

for the particle and

(7c,d)

for the fluid.

The boundary conditions for the magnetic field at the particle surface and cavity wall are

(8a)

; (8b)

(9)

Equations (8a) and (8b) denote that the normal component of the magnetic flux density and the tangential component of the magnetic field, respectively, are continuous at the particle surface, whereas Equation (9) leads to the imposed magnetic flux density everywhere in the fluid in the absence of the particle.

The solution to Equations (7)-(9) with the substitution of Equations (4) and (5) can be expressed as

, (10a)

, (10b)

where the magnetic scalar potential distributions caused by the applied field are

, (11a)

, (11b)

and. The constant terms in Equation (11) are trivial and have been neglected.

The first terms on the right-hand side of Equation (10) are the magnetic flux densities induced by the applied electric current density (Ampere’s law), whereas the second terms are those resulting from the applied magnetic field. The magnitude of either ratio of the first-to-second terms has the order, which is usually small [22] .

2.3. Electromagnetophoretic Force and Velocity

The creeping motion of the Newtonian fluid in the presence of the applied magnetic flux density and electric current density is governed by the Stokes equations with a Lorentz force density term,

, (12a)

, (12b)

where and are the fluid velocity and dynamic pressure distributions, respectively. Note that, different from the constant force density in a gravitational field, the Lorentz force density is a function of position in the particle and fluid phases.

The boundary conditions for the fluid velocity at the no-slip particle surface and cavity wall are given by

, (13)

, (14)

where is the EMP migration velocity of the particle to be determined. There is no rotation of the particle due to the axial symmetry of the fluid flow.

Following Teubner’s approach to obtain the particle velocity (without solving for the fluid velocity field) with a generalized reciprocal theorem [33] - [37] , we can express the EMP force exerted on the confined particle as

, (15)

where the total applied force acting on the particle is composed of relevant surface and volume integrals,

. (16)

Here, is the hydrodynamic resistance coefficient for the migration of the sphere driven by a body force field in the concentric spherical cavity,

; (17)

is the magnetic Maxwell stress tensor,

; (18)

, (19a)

, (19b)

and is the unit dyadic.

In Equation (16), the first term on the right-hand side is the Lorentz body force exerted directly on the particle, known as the electromagnetic weight, the second term is a force contribution from the fluid flow due to the Lorentz force density in Equation (12a), and the third term represents the contribution from the Maxwell stress at the particle surface. equals, which is the applied Lorentz force acting on the fluid volume occupied by the particle, known as the electromagnetic buoyancy.

Substituting Equations (4) and (5) for the electric current density distributions and Equations (10) and (11) for the magnetic flux density distributions into Equations (15) and (16), we obtain the ensuing migration velocity of the particle

, (20)

where the dimensionless EMP mobility of the particle

, (21)

and the coefficients and are functions of the particle-to-cavity radius ratio,

, (22a)

. (22b)

Evidently, is a function of the particle-to-fluid electric conductivity ratio and magnetic permeability ratio as well as only. For the special case of (the particle and suspending fluid have the same electric conductivity and magnetic permeability), the electromagnetic weight (and the total applied force acting on the particle) equals the electromagnetic buoyancy and there is no particle motion. If only the first term on the right-hand side of Equation (16) is taken approximately to be the total applied force in Equation(15) [23] , then Equation (21) becomes

, (23)

which is the same as a corresponding formula obtained recently [37] .

Note that Equation (20) predicts to be bilinear in the product, indicating that the integral terms of the second orders and in the Maxwell stress and Lorentz force densities and in Equation (16) vanish and make no contribution to the particle velocity. Nonetheless, the contribution from the induced magnetic flux density caused by the applied electric current density [the first term on the right-hand side of Equation (10b)] is included in Equation (21) via the term containing in Equation (16). For a particle with in aqueous solutions with the applied electric current density and magnetic flux density, the characteristic particle velocity in Equation (20) is about typically.

In the limit (the cavity wall is at an infinite distance from the particle), Equation (21) reduces to

. (24)

If the term of integration of the Maxwell stress over the particle surface in Equation (16) is not included, Equation (24) becomes

. (25)

This approximate result (depending on and symmetrically) agrees with the EMP mobility calculated using the formula obtained earlier by Leenov and Kolin [24] for the EMP force acting on a spherical particle in an unbounded fluid with, in which the effect of the Maxwell stress was not considered. Note that the EMP mobility at predicted by Equation (25) is much smaller than that resulting from Equation (24) by a factor of 3/7, and thus the contribution from the Maxwell stress (only due to its part bilinear in and) to the EMP migration of a particle is significant in spite of that the ratio of the first-to-second terms in Equation (10b) is small.

In the limit (the particle fills the cavity up completely), Equation (21) results in, as expected.

3. Results and Discussion

Equation (20) for the EMP migration of a spherical particle positioned at the center of a spherical cavity indicates that the velocity of the particle is bilinear in the applied electric current and magnetic flux density fields (and proportional to). The results of the dimensionless EMP mobility obtained in Equations (21) and (24) for the confined particle and an isolated particle, respectively, as well as the asymptotic behaviors of the boundary effect on the EMP migration as and will be discussed in this section.

3.1. Electromagnetophoretic Mobility Parameter U^*

We first plot the EMP mobility parameter of an unconfined spherical particle as calculated from Equation (24) in Figure 2 for various values of the particle-to-fluid electric conductivity ratio and magnetic permeability ratio. As can be derived from Equation (24), is always positive if and negative if, regardless of the value of. In the intermediate range of, is positive (negative) if the value of is sufficiently large (small). For a constant value of, the value of increases monotonically with an increase in from a negative constant at to a positive one as. For a specified value of greater than, the value of increases monotonically with an increase in, whereas for a given value of less than, is negative and decreases monotonically with an increase in. When, , independent of. Equation (24) gives , , , and in the limits of approaching, , , and, respectively.

The normalized EMP mobility of a confined particle calculated from Equations (20) and (24) as a function of the particle-to-cavity radius ratio is plotted in Figure 3 for limiting conditions of the parameters and. In general, decreases monotonically with an increase in from unity at to zero at for specified values of and. However, for the case of large (thus, is positive) and small (e.g., a superconducting particle), first decreases with an increase in from unity at, reaches a minimum of negative value (implying a reversal in the direction of particle migration), then increases with further increase in to zero at. In this case, the second term on the right-hand side of Equation (16) dominates the force exerted on the particle and results in the non-monotonic dependence of on. For a constant value of, decreases (or the boundary effect becomes stronger) with an increase in and increases (or the boundary effect gets weaker) with an increase in, keeping the other parameter unchanged. The boundary effect of the cavity on the EMP mobility of the particle is equivalent to that caused by gravitational fields [30] (in the particular case of and, for an arbitrary value of and the boundary effect on the EMP migration or magnetohydrodynamic migration of a spherical nanomotor [37] is exactly the same as that on sedimentation), but is much stronger than that in electrophoresis [31] .

3.2. Asymptotic Behaviors of the Boundary Effect on Electromagnetophoresis

Yariv and Miloh [27] analyzed the EMP motions of an insulating spherical particle suspended in a conducting fluid of matching magnetic permeability (i.e., with and) in the vicinity of a dielectric plane

wall, where an electric current is imposed parallel to the wall and a perpendicular magnetic field is applied either parallel or normal to the wall. Through the use of a method of reflections for the situation of wide separation, they obtained formulas for the hydrodynamic force on the particle and the migration velocity of the particle in asymptotic expansions of, the ratio of the particle radius to the distance of the particle center from the wall. The leading-order wall-induced corrections to the EMP force and migration velocity appear to be and, respectively, as opposed to the variation for both the resistance and the mobility of a sphere undergoing sedimentation near a plane wall.

The Taylor expansions for the EMP force and migration velocity of a spherical particle with within a concentric spherical cavity in resulting from Equations (15) and (20) together with Equations (17), (21), and (22) are

, (26a)

. (26b)

Here, the leading-order corrections to the EMP force and migration velocity also appear at and, respectively, in contrast to the correction given by Equation (17) for both the resistance and the mobility of a sphere settling at the center of a spherical cavity. The wall effect in Equation (26b) is to hinder the EMP migration velocity of the particle, whereas Equation (26a) indicates that the boundary tends to augment (reduce) the hydrodynamic force exerted on the particle if, under the situation of, the value of is smaller (greater) than 1/3. As expected, the boundary effect of the enclosing cavity wall on the EMP migration is much stronger than that of a neighboring plane wall predicted by Yariv and Miloh [27] , in which, same as in the analysis by Leenov and Kolin [24] , the contribution from the Maxwell stress in Equation (16) was not included.

It is also interesting to examine the asymptotic behavior of the boundary effect on EMP migration for the situation of near contact between the particle and the concentric cavity wall. The Taylor expansions for the EMP force and migration velocity of the confined particle with in resulting from Equations (15) and (20) are

,(27a)

. (27b)

Equation (27b) illustrates that the migration velocity of the EMP particle decays with an increase in as the order, same as that resulting from Equation (17) for a sphere migrating under gravity at the center of a spherical cavity. However, Equation (27a) indicates that the EMP force on the particle is finite (as long as) at [with the leading-order correction at in the direction depending also on the sign of (at)], as opposed to the divergent asymptotic behavior with the order for the hydrodynamic force on a settling sphere in a concentric spherical cavity. Note that the wall-corrected EMP force and migration velocity of the particle with are proportional to as and to as; when (the particle and suspending fluid have the same electric conductivity), there is no EMP motion.

4. Summary

In this work, the EMP migration of a spherical particle situated at the center of a spherical cavity filled with a conducting fluid subject to uniformly applied electric and magnetic fields is analyzed at the quasi-steady state. After solving the electric current and magnetic flux density distributions in the particle and fluid phases of arbitrary electric conductivities and magnetic permeabilities, the Stokes equations modified with the resulted Lorentz force density for the fluid motion are treated by a generalized reciprocal theorem, and the EMP migration velocity of the particle is obtained explicitly in Equations (20)-(22). The effect of the Maxwell stress, which was neglected in previous studies, on the EMP force and velocity of the particle is found to be significant. The migration velocity of the particle in general decreases monotonically with an increase in the particle-to-cavity radius ratio, with an exception for the case that the electric conductivity ratio is large and the magnetic permeability ratio is small, where the particle may reverse its direction of migration with the variation in. At the touching limit, the particle velocity vanishes, but the EMP force acting on the particle is finite. The boundary effect on the EMP migration of the particle, which increases with an increase in and decreases with an increase in, is equivalent to that on its sedimentation, but is much stronger than that on its electrophoretic motion.

Acknowledgements

This research was supported by the National Science Council of the Republic of China.

References