Journal of Electromagnetic Analysis and Applications
Vol.6 No.7(2014), Article
ID:47266,7
pages
DOI:10.4236/jemaa.2014.67015
4D Integration and Evaluation of Electrostatic Force between Two Charged Parallel Plates
Haiduke Sarafian
Pennsylvania State University, University College, USA
Email: has2@psu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 6 May 2014; accepted 1 June 2014
ABSTRACT
Evaluation of electrostatic force between two arbitrary shaped charged objects encounters a sixfold integration. Analytic evaluation of the integral is not conducive and its numeric evaluation is CPU intensive. For two planar objects, the required integration reduces to a four-fold integration; however, it suffers the same two symptoms. In this article, utilizing a discrete method, we evaluate the much needed integration in a fraction of a second. For a special case, we show the output of our approach agrees with its analytic equivalent formulation.
Keywords:4D Integration, Force between Plates, Mathematica

1. Introduction
Most of the electrostatic scenarios are based on a two-body point-like charge-charge interaction and/or equally the corresponding potential issues. As such, a charged object is viewed as if it is made of collected point-like charges so that the superposition of the charge-charge interaction is applied. Theoretically, this is sound; however, in practice one encounters challenging mathematical as well as computational issues. For instance dicing two arbitrary shaped charged objects in pieces yields numerous point-like charges. The product of any two of these charges divided by the squared distance between them is the differential representative electrostatic force. The overall interaction comes about by integrating the latter over each of the objects. The objects in general are 3D, and such, the evaluation of the interaction requires a six-fold coordinate dependent integration. Even a pair of “simple” 3D objects in practice are not immune yielding no analytic solution. In practice it is also proven the numeric integration of a six-fold integral is CPU intensive. For instance, a 2.5 GHz double processor laptop runs three-and-half hours yielding no result! In other words, neither one of these two methods are practical. Aside from theoretical curiosities, in real-life and for practical purposes one needs to resolute the interactions between two less complicated looking objects such as two flat plates. e.g. the plates of a parallel-plate capacitor. In the latter, the six-fold integration reduces to a four-fold integral. The integration is challenging, and the calculation is cumbersome. Its numeric integration is still CPU intensive. In other words, repeating the computation for different relevant parameters is time consuming, requires plenty of patience and is inefficient. With these counterproductive experiences, we devise an efficient and practical numeric approach which is fast and accurate. It is the objective of this work to discuss the details. We craft a four-segment article. In addition to Motivation and Objectives, in Section 2 we brief three relevant scenarios; this lays the foundation for tackling the main project. In Section 3 for a special case we investigate an interaction conducive to an analytic formulation, and, we show our approach numerically matches its analytic version. In Section 4, we close the article with concluding remarks paving the road for the future investigations.
2. Formulation of the physics problem
Case 1. We begin evaluating the force that a uniformly charged line exerts on a point-like charge. We denote the length of the line, its charge and charge density , respectfully. The force on a point-like charge q positioned along the extension of the line x-distance away trivially evaluates, [1]
, respectfully. The force on a point-like charge q positioned along the extension of the line x-distance away trivially evaluates, [1]
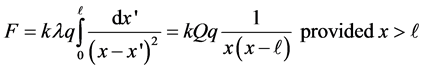 , (1)
, (1)
where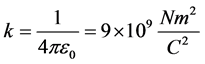 . Next for the scenario depicted in Figure 1, we evaluate the force assuming the charged line is diced in n equal pieces each carrying an equal charge,
. Next for the scenario depicted in Figure 1, we evaluate the force assuming the charged line is diced in n equal pieces each carrying an equal charge, . By superposing the differential forces we arrived at,
. By superposing the differential forces we arrived at,
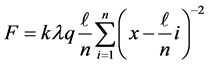 . (2)
. (2)
Figure 2 is the plot of these two forces vs. the distance x. For the sake of comparison the vertical axis is scaled to F/kQq. The curves are the integral and sum terms of Equations (1) & (2) for . By trial and error we justify that a reasonable value for the number of the segments is n = 100. Mathematica V9.0 [2] takes only a fraction of a second to generate the result.
. By trial and error we justify that a reasonable value for the number of the segments is n = 100. Mathematica V9.0 [2] takes only a fraction of a second to generate the result.
For the sake of clarity the gray curve is thickened. Its actual thin plot overlaps perfectly with the plot of Equation (2).
Case 2. In this scenario we envision aligning two identically charged nano-tubes separated by a distance x, shown in Figure 3. We assume each tube has the length, charge and charge density , q and
, q and , respectively. Applying the superposition of the differential forces gives,
, respectively. Applying the superposition of the differential forces gives,
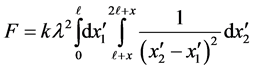 (3)
(3)
this yields,
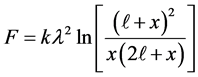 (4)
(4)
Similar to the procedure described in Case 1, we dice the tubes in n and m pieces, respectively. The overall force comes about by adding all the two-body paired forces, that is,
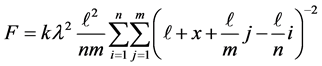 (5)
(5)

Figure 1. Display of a charged line and a point-like charge situated along the x-axis.

Figure 2. Plots of the integral and sum terms of Equations (1) & (2). The thick gray curve is the plot of the analytic (Equation (1)) and the solid curve is its summed version (Equation ( 2)).

Figure 3. Display of two aligned charged nano-tubes of length  separated by a distance x.
separated by a distance x.
For the sake of clarity the gray curve is plotted with an over-sized thickness. The actual thin curve overlaps perfectly vs. the plot of Equation (5). As shown in Figure 4, the agreement between the analytic calculation and its discrete version is perfect. We have achieved this high precession by applying a (n × m) = (5 × 5) grid. The computation time is a fraction of a second.
Case 3. Here we consider a pair of identically charged parallel nano-tubes. We place the tubes along the y-axis separating them by a distance y, as shown in Figure 5. The rest of the physical parameters are the same as Case 2. The basic difference between the current case vs. Case 2 is the orientation of the differential force; the latter is a two-component slanted force. Applying the superposition of the differential forces along the horizontal and vertical axis yields,
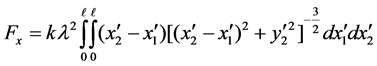 (6)
(6)
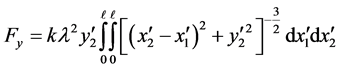 (7)
(7)
Symbolic computation of these two integrals is challenging. Mathematica takes quite some time to produce outputs. However, if one sets numeric values for 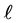 and
and  the task at hands runs reasonably fast. For the sake
the task at hands runs reasonably fast. For the sake
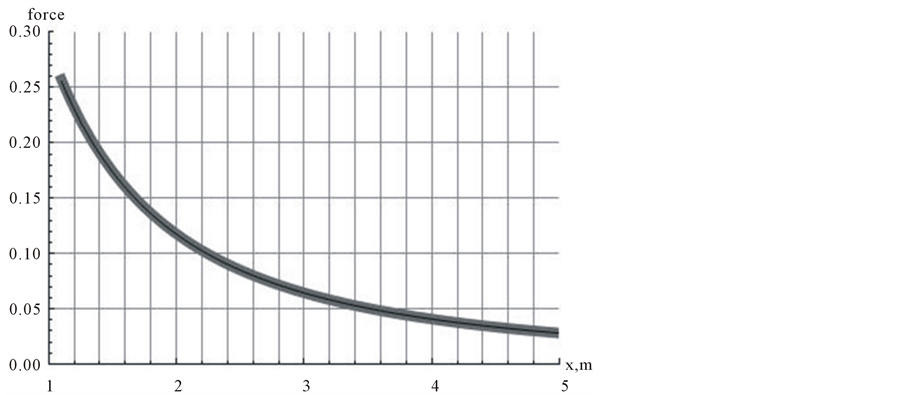
Figure 4. Plots of Equations (4) & (5). The thick gray curve is the analytic (Equation(4)) and the solid curve is its summed version (Equation(5)).

Figure 5. Display of two charged parallel nano-tubes. Tubes are identical in length carrying the same charge densities.
of demonstration we choose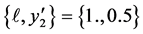 . In 3.75 minutes the output is {Fx, Fy} = {0, 2.47}. Meaning, the symmetry of the aligned nano-tubes vanishes the x-component, Equation (6), while itsy-component, Equation (7), is nonzero. Although the CPU time of the computation is reasonably short, repetition of the computation for varying y becomes an issue. To remedy this as in Case 2, we convert Equations (6) & (7) into discrete formats. These are,
. In 3.75 minutes the output is {Fx, Fy} = {0, 2.47}. Meaning, the symmetry of the aligned nano-tubes vanishes the x-component, Equation (6), while itsy-component, Equation (7), is nonzero. Although the CPU time of the computation is reasonably short, repetition of the computation for varying y becomes an issue. To remedy this as in Case 2, we convert Equations (6) & (7) into discrete formats. These are,
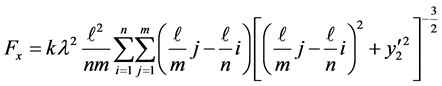 (8)
(8)
 (9)
(9)
Applying Equations (8) & (9) for a chosen  and n = m = 50 yields the same output {0, 2.47} in a fraction of a second. By varying the value of
and n = m = 50 yields the same output {0, 2.47} in a fraction of a second. By varying the value of  within the range 0.05, 0.10, 0.15, ..., 0.85 we evaluate repeatedly Equation (9). The plot of these values is shown in Figure 6. The vertical axis of Figure 6 is scaled to kλ2. As shown and intuitively expected the vertical component of the force is stronger for a short separation distance between the nano-tubes and is weaker for the large separation distances.
within the range 0.05, 0.10, 0.15, ..., 0.85 we evaluate repeatedly Equation (9). The plot of these values is shown in Figure 6. The vertical axis of Figure 6 is scaled to kλ2. As shown and intuitively expected the vertical component of the force is stronger for a short separation distance between the nano-tubes and is weaker for the large separation distances.
It is noted that by reducing the size of the double sum from a 50 × 50 grid to a smaller grid size gives a reasonable acceptable output. However, since the CPU time of the discrete summation is quite short in practice one would prefer keeping the grid size reasonably large.
Case 4. This case deals with computation of the force between two charged plates. This is a natural extension of the cases discussed previously. There are numerous options for positioning the two plates; our interest is to position them evenly parallel. The interested reader may extend the approach for asymmetric and non-parallel plates. Here we assume each plate is a square of side length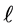 with a uniform charge density,
with a uniform charge density,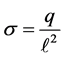 . We place the plates along the z-axis, parallel to the xy-plane z0 apart, as shown in Figure 7. Because of the symmetry, the horizontal component of the force vanishes. Envisioning the plates are composed of tiny cells the overall force comes about by integrating over the differential force between the pairs. Applying the superposition principle yields the non-vanishing, vertical component of the force.
. We place the plates along the z-axis, parallel to the xy-plane z0 apart, as shown in Figure 7. Because of the symmetry, the horizontal component of the force vanishes. Envisioning the plates are composed of tiny cells the overall force comes about by integrating over the differential force between the pairs. Applying the superposition principle yields the non-vanishing, vertical component of the force.
 (10)
(10)
As one may imagine this 4D integration would not yield a symbolic output. Its numeric integration is also hopelessly CPU intensive. Following the lessons practiced in the previous cases we convert Equation (10) into discrete format, this gives,
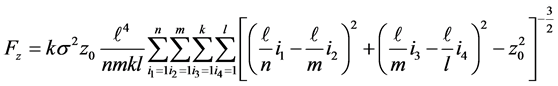 (11)
(11)
To optimize the output of Equation (11) we consider four different grid sizes; {n, m, k, l} = {2,2,2,2}, {3,3,3,3}, {4,4,4,4} and {5,5,5,5}. Applying these grid options, in Figure 8 we display the variation of the Fz vs. z0.
As shown, for the large separation distances, e.g.  the output of the numeric computation is independent to the number of the cells within the grid, while for the short distances it is sensitive to the latter. Plots show a converging trend. Namely, the rate of convergence from a grid size a {2, 2, 2, 2} to a {5, 5, 5, 5} is not linear. Meaning, by increasing the grid size to an {8, 8, 8, 8} would produce an output comparable to the {5, 5, 5, 5}.
the output of the numeric computation is independent to the number of the cells within the grid, while for the short distances it is sensitive to the latter. Plots show a converging trend. Namely, the rate of convergence from a grid size a {2, 2, 2, 2} to a {5, 5, 5, 5} is not linear. Meaning, by increasing the grid size to an {8, 8, 8, 8} would produce an output comparable to the {5, 5, 5, 5}.
3. Alternative Physics Perspective
For a two charged parallel plate arrangement one may directly formulate the needed force applying the potential energy approach. As such, since we assumed the plates are identically charged, the repulsive force between the plates would have a tendency to push the plates apart. An external force would be needed to keep the plates in place. The needed force is the variation of the electrostatic potential energy of the assembly over the variation of the separation distance between the plates, i.e. 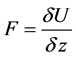 [1] . For a parallel-plate arrangement the electrostatic potential energy is U = 1/2 q2/C, where q is the charge of one of the plates and C is the capacitance of the arrangement [3] . For the case at hand,
[1] . For a parallel-plate arrangement the electrostatic potential energy is U = 1/2 q2/C, where q is the charge of one of the plates and C is the capacitance of the arrangement [3] . For the case at hand,  with
with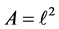 . Manipulating these equations yields,
. Manipulating these equations yields,
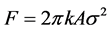 . Throughout this article we suppressed the relevant common electrostatic parameters, such as
. Throughout this article we suppressed the relevant common electrostatic parameters, such as . Following the same strategy, here too, in the latter equation we realize the only uncounted value is the factor 2
. Following the same strategy, here too, in the latter equation we realize the only uncounted value is the factor 2 . The vertical axis in Figure 8 is the scaled value of the force. The newly evaluated value of the force is a factor 6.28 and it can conveniently be compared to the values depicted in Figure 8. Meaning, as shown, a horizontal line with an ordinance of a 6.28 crosses the curves at different abscissa confirming the ac-
. The vertical axis in Figure 8 is the scaled value of the force. The newly evaluated value of the force is a factor 6.28 and it can conveniently be compared to the values depicted in Figure 8. Meaning, as shown, a horizontal line with an ordinance of a 6.28 crosses the curves at different abscissa confirming the ac-
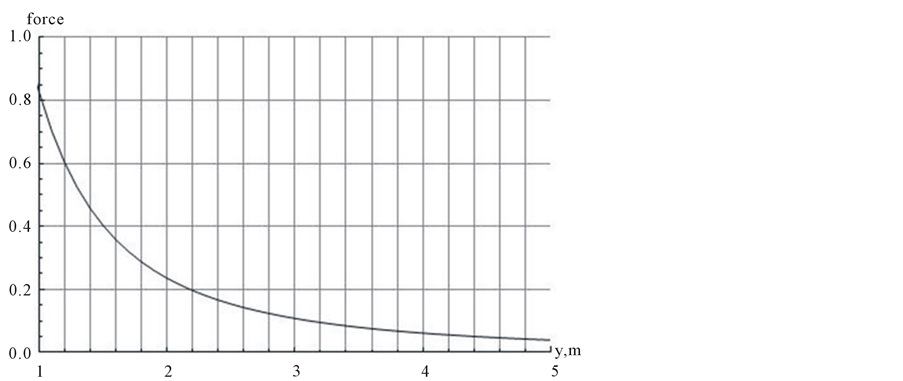
Figure 6. Display of Equation (9) for l = 1 and n = m = 50.
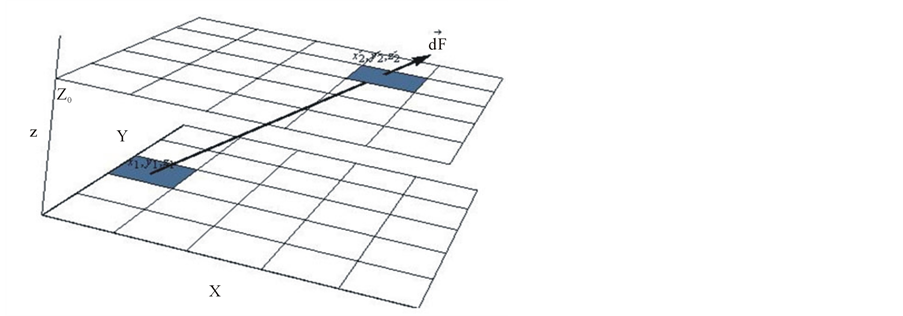
Figure 7. Two charged parallel plates separated by a distance z0. Plates are identical square; each one is subdivided in a 5 × 5 cells.

Figure 8. Plots of Equation (11) for various grid sizes. The solid curve corresponds to {n, m, k, l} = {5,5,5,5}. The curves deviating from the solid curve outward correspond to a {4,4,4,4}, {3,3,3,3} and {2,2,2,2}, respectively.
curacy of the applied discrete computation. As a best answer among four possible choices one wisely should select the shortest abscissa corresponding to the shortest separation distance z0 = 0.1 m. This is the best choice because at such a short separation distance the ratio of the size of the plate to the separation distance i.e. is at its largest. This corresponds to the weakest fringing effects of the electric field at the edges of the plates, justifying the usage of the capacitance of the capacitor, .
.
4. Conclusion
In the area of electrostatic one routinely encounters high dimensional integrations. In the course of our investigation we point out a few. In most cases, the integrations are not analytically calculable and numeric integrations are CPU intensive. By converting the analytic integrations to a discrete format, we are able to evaluate the needed integrations. Concluding the proposed method can be confidently applied to vast areas of computational physics. As a future research project, the interested reader may apply the method for an e.g. two non-parallel charged plates.
References
- Jackson, J.D. (1998) Classical Electrodynamics. 3rd Edition, Wiley, New York.
- Wolfram, S. (2012) Mathematica, V9.0, a Computational Software Program to Do Scientific Computation. Wolfram Research.
- Giordano, N.J. and Nakanishi, H. (2006) Computational Physics. 2nd Edition, Prentice Hall, Upper Saddle River.

