Journal of Electromagnetic Analysis and Applications
Vol.6 No.1(2014), Article ID:42207,7 pages DOI:10.4236/jemaa.2014.61002
Monte Carlo Computer Simulation of Nonuniform Field Emission Current Density for a Carbon Fiber
1Voronezh State University of Architecture and Civil Engineering, Voronezh, Russia; 2Moscow Institute of Physics and Technology (State University) (MIPT (SU)), Moscow, Russia.
Email: golovinski@bk.ru
Received October 30th, 2013; revised November 29th, 2013; accepted December 21st, 2013
ABSTRACT
The field emission current from a carbon fiber is considered. As a model of emission of an elementary carbon tube, tunnel ionization of an electron from a short-range potential is taken. The exact solution for the wave function in such a model allows obtaining an asymptotic expression for electron current. A computer model of transverse distribution of emission current of a carbon fiber is built on the basis of the Monte Carlo method that allows taking into account the random character of distribution of local emitter sources and the distribution of gains of an electric field in carbon nanotubes.
Keywords:Field Emission; Carbon Fiber; Current Density; Short-Range Potential; Monte Carlo Method
1. Introduction
Carbon nanotubes (CNT) can be grown in the form of small sharp spikes capable of withstanding considerable electric current densities. This assumes high potentialities of application of CNT as field emission cathodes in highpower vacuum devices. Such devices with field emission cathodes seem to be ideal for space applications [1] including disinfection means. New electrical, mechanical, and thermal properties of CNT have attractive characteristics for producing stable currents of high density with relatively low electric fields. The comparative analysis of different properties of field emission cathodes is given in [2], and the review of technological features of manufacturing emitters based on nanotubes is in [3], where it is noted also that, besides application in high-power visible and near-UV light sources, field emitters based on CNT are promising for X-ray minilamps, electron microscopy, and microdiodes.
The emission properties of an individual nanotube are described on the basis of the Fowler-Nordheim model [4,5] based on the phenomenon of quantum-mechanical tunneling of an electron under a barrier under the action of a constant electric field. The current density in such a model is determined by the dependence
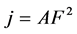 , where
, where 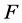 is the electric field strength,
is the electric field strength, 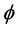 is the electron work function,
is the electron work function, 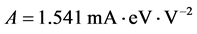
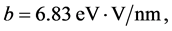 [6]. It should be noted that this formula was initially obtained for metal emitters, and its application to nanotubes requires introduction of certain corrections. More exact formulas for field emission current take into account an additional polarization potential [7].
[6]. It should be noted that this formula was initially obtained for metal emitters, and its application to nanotubes requires introduction of certain corrections. More exact formulas for field emission current take into account an additional polarization potential [7].
In practice, field emitters in the form of a CNT array contain a very great number of individual nanotubes that differ from one another by their geometry, degree of alignment, electronic features, and other parameters [8,9]. Due to different dependence of emission currents of individual CNT on the electric field strength near a tip, the main contribution to emission is made by a relatively small number of nanotubes with the highest electric field gain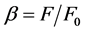 . In the emitter of CNT, the value
. In the emitter of CNT, the value 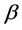 depends not only on the aspect ratio (the ratio of the length to the diameter) for an individual nanotube, but also on the geometry and density of CNT in the array with a maximum at an average distance between nanotubes of the order of height of individual CNT.
depends not only on the aspect ratio (the ratio of the length to the diameter) for an individual nanotube, but also on the geometry and density of CNT in the array with a maximum at an average distance between nanotubes of the order of height of individual CNT.
Investigations carried out earlier showed that emitter nonuniformities influenced the current density, but they did not give an answer to the question about the transverse nonuniformity of the current itself in its propagation from the cathode to the anode. At the same time, this nonuniformity directly affects also the nonuniformity of secondary radiation caused by the emission current in a target. To solve this problem, we will consider a model based on taking into account the contribution of electronic amplitudes to the expression for the total current in case of three-dimensional tunnel ionization of different ways arranging point sources.
2. Mathematical Model of Short-Range Potential
To describe the propagation of an electron wave in a constant uniform electric field, we will choose a model, in which each individual nanotube is a point source of electron waves. Let us consider a point source, in which an electron is bound by a short-range potential [10]:
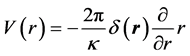 (1)
(1)
at the energy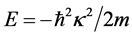 . The Schrödinger steadystate equation describing the decay of a quasi-stationary state in the constant uniform electric field with the strength
. The Schrödinger steadystate equation describing the decay of a quasi-stationary state in the constant uniform electric field with the strength 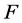 looks like
looks like
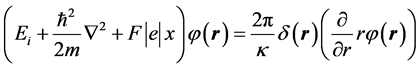 (2)
(2)
The solution of the Equation (2) is expressed in terms of the Green function 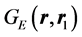 of the Schrödinger steady-state equation for an electron in a uniform electric field [11,12]:
of the Schrödinger steady-state equation for an electron in a uniform electric field [11,12]:
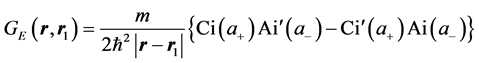 (3)
(3)
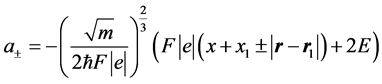
The function  is expressed in terms of the ordinary Airy functions
is expressed in terms of the ordinary Airy functions 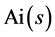 and
and 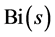 [13]:
[13]: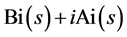
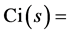 . The OX axis is directed oppositely to the direction of the electric field
. The OX axis is directed oppositely to the direction of the electric field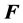 . The equation for
. The equation for  looks like the Equation (2) with substitution of the point nonuniformity
looks like the Equation (2) with substitution of the point nonuniformity  for the right side. At
for the right side. At 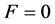 the solution of the Equation (2) is
the solution of the Equation (2) is
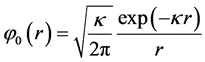 (4)
(4)
The Equation (2) can be written as the equivalent integral equation
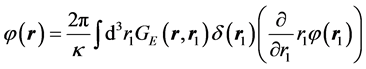 (5)
(5)
In the three-dimensional 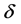 -potential [14] in the limit of a weak field the polarizability of a level is
-potential [14] in the limit of a weak field the polarizability of a level is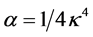 , and its width is
, and its width is
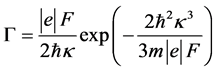 (6)
(6)
Substituting the undisturbed wave function (4) in the right side of the Equation (5), we will obtain
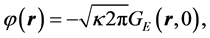 (7)
(7)
and the current density at a great distance from the source is proportional to the squared absolute value of the wave function:
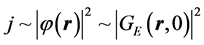 (8)
(8)
For convenience of calculations it is advisable to write the solution in the asymptotic form:
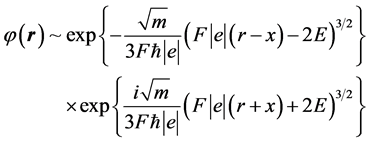 (9)
(9)
At great distances from the source in the paraxial region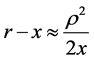 ,
, 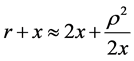 , where
, where  is the distance from the OX axis. Using the condition
is the distance from the OX axis. Using the condition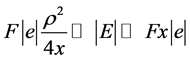 , we will obtain in the paraxial region:
, we will obtain in the paraxial region:
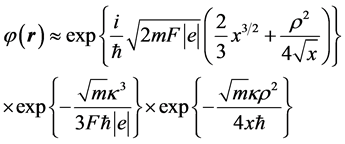 (10)
(10)
As a result, for the current from one point source we have the transverse distribution
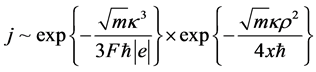 (11)
(11)
Shown in Figure 1 is the transverse distribution of electron current calculated by the formula (8) with the true Green function and by the asymptotic formula (11).
The comparison of the curves shows the high accuracy of the asymptotic representation at a specified distance.
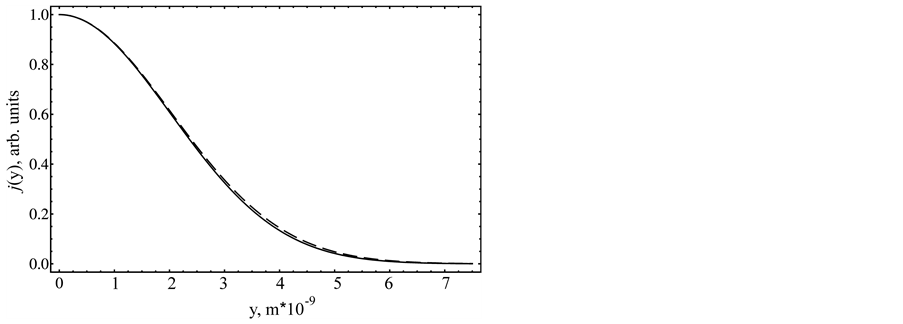
Figure 1. The transverse current distribution for the distance 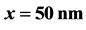 and the electric field strength F =
and the electric field strength F =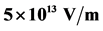 : exact solution is solid curve, asymptotic representation is dotted curve. The electron binding energy is
: exact solution is solid curve, asymptotic representation is dotted curve. The electron binding energy is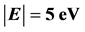 .
.
At longer distances the accuracy becomes still higher. So for practical calculations it is advisable to use just asymptotic expressions.
For several coherent centers the current density is
 (12)
(12)
where summation is made over all coherent sources.
Figure 2 shows the result of calculation of superposition of coherent electron waves from two point sources. The distance to the screen and the binding energy correspond to Figure 1. The distance between the sources is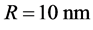 .
.
In Figure 2 it is well seen that in the region of overlapping of coherent waves interference shows itself.
3. Results of Computer Simulation
The statistical treatment of the values of the work function for nanotubes gives an average value of the work function of 5.3 eV. It does not differ greatly from a corresponding value for graphite. In this case a usual electron energy spread is 0.3 eV. Moreover, if the source of field emission electrons is a carbon fiber, the emitter surface is very nonuniform and consists of randomly oriented carbon nanotubes, or has a flaky fibrillar structure [15]. A characteristic number of fibrils in an emitter with an end area of 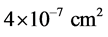 is up to 4000 elements. Accordingly, for each nanotube there is its own field gain
is up to 4000 elements. Accordingly, for each nanotube there is its own field gain 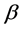 that obeys the normal distribution law
that obeys the normal distribution law
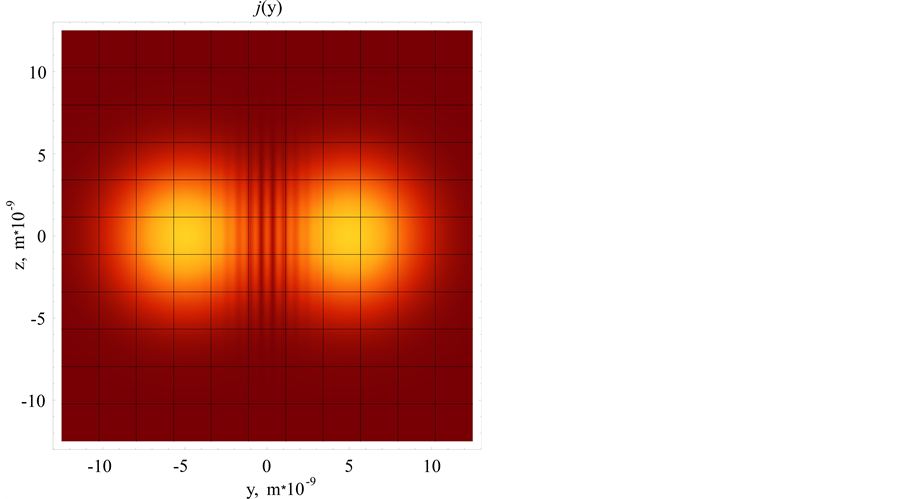
Figure 2. The structure of interference fringes in interference of two coherent electron waves.
 (13)
(13)
The value typical of experiment treatment is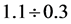
 , and gains themselves vary in the range
, and gains themselves vary in the range![]()
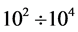 [8]. Such a spatial nonuniformity as well as strong temporal current fluctuations [16] exclude interference effects, and the current density becomes the sum of currents of individual sources of the ensemble:
[8]. Such a spatial nonuniformity as well as strong temporal current fluctuations [16] exclude interference effects, and the current density becomes the sum of currents of individual sources of the ensemble:
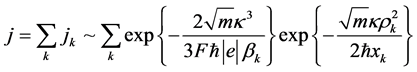 (14)
(14)
The nonuniformity of distribution of field gain over the emitter surface is confirmed by the results of direct measurement with the use of a scanning anode tunnel emission microscope [5]. At the same time, observed in this work was the distribution of field emission current density for a carbon emitter by luminescence on a luminescent screen. As the field changed from 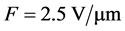 to
to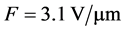 , on the 1.1 cm ´ 0.7 cm screen a sharp increase of the total exposure field and increasing luminescence uniformity were observed. The planar emitter sample under study had 164 point emitters located on an area of
, on the 1.1 cm ´ 0.7 cm screen a sharp increase of the total exposure field and increasing luminescence uniformity were observed. The planar emitter sample under study had 164 point emitters located on an area of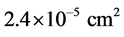 , that is, with a surface density of point sources of
, that is, with a surface density of point sources of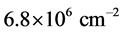 .
.
To calculate the transverse distribution of electron emission current over a target, the Monte Carlo method was used [17]. To simulate a planar emitter with random arrangement of local sources, they should be arranged on a plane with a uniform probability density as shown in Figure 3. The minimum distance between individual sources is limited by the parameter 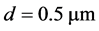 that makes it possible to avoid superposition of sources, that is, to take into account the excluded volume effect.
that makes it possible to avoid superposition of sources, that is, to take into account the excluded volume effect.
In this case it is necessary, besides coordinates, to specify the field gain ![]() for each source that is chosen according to the random distribution (13).
for each source that is chosen according to the random distribution (13).
An ordinary random number generator gives a uniform distribution in the interval (0,1). For an arbitrary density of distribution 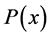 the distribution function [18] is determined by the relation
the distribution function [18] is determined by the relation
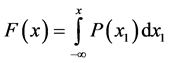 (15)
(15)
Since the density of distribution is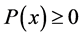 , the distribution function is a monotonically increasing function of
, the distribution function is a monotonically increasing function of  from
from 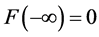 to
to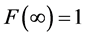 . This gives the single-valued inverse function
. This gives the single-valued inverse function
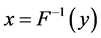 (16)
(16)
if . If now we in a random manner generate numbers
. If now we in a random manner generate numbers  in the interval (0,1) with a uniform density, they will be mapped into a required distribution by the function
in the interval (0,1) with a uniform density, they will be mapped into a required distribution by the function 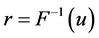 [19].
[19].
For the normal distribution (13)
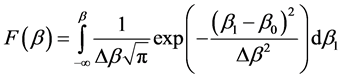 (17)
(17)
which in view of the determination of the error function [17]
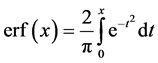 (18)
(18)
can be written as
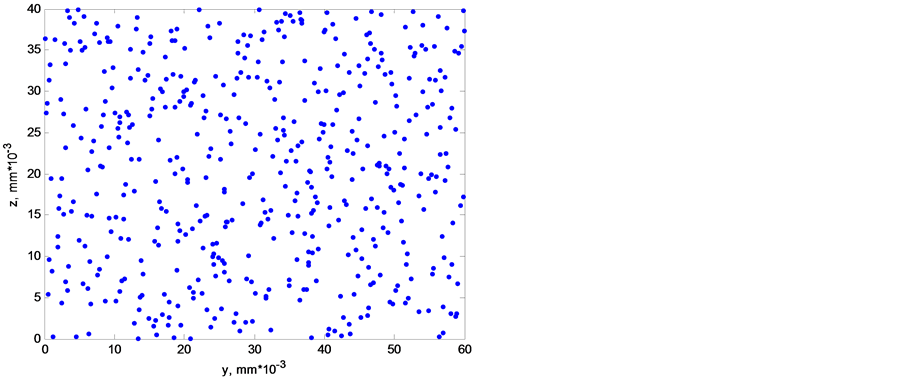
Figure 3. The random arrangement of sources with excluded volume.
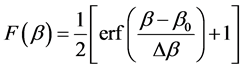 (19)
(19)
Shown in Figure 4 are the results of calculation of the distribution of current density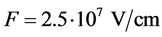 ,
, 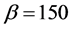 for different distances
for different distances ![]() between the emitter and the screen.
between the emitter and the screen.
The results of calculations show high nonuniformity of transverse distribution of current density that decreases with growing number of point sources, field strength, and distance from the emitter to the screen. The ratio of the minimum current density to the average value  increases with distance from 0 to 0.5. The ratio of the maximum current density to the average value
increases with distance from 0 to 0.5. The ratio of the maximum current density to the average value  decreases with growing distance to the screen from 4.6 to 3. In this case the spread of values estimated by the ratio of dispersion to the average value
decreases with growing distance to the screen from 4.6 to 3. In this case the spread of values estimated by the ratio of dispersion to the average value 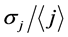 remains high at a level of
remains high at a level of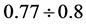 . This result should be assigned first of all to great fluctuations of density of arrangement of individual sources on the emitter surface.
. This result should be assigned first of all to great fluctuations of density of arrangement of individual sources on the emitter surface.
For comparison, shown in Figure 5 are the results of computer simulation in case of location of sources at points of a perfect square lattice at  and with a step for lattice points of 4 mm. In this case the dimensions of regions with uniform current density are increased considerably, and low current densities are retained only on the edges of the screen. The ratio of the maximum density to the average value is
and with a step for lattice points of 4 mm. In this case the dimensions of regions with uniform current density are increased considerably, and low current densities are retained only on the edges of the screen. The ratio of the maximum density to the average value is 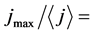
![]() , and the relative dispersion is
, and the relative dispersion is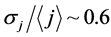 . Thereby it was demonstrated that the regular arrangement of emission microsources increases significantly the current uniformity.
. Thereby it was demonstrated that the regular arrangement of emission microsources increases significantly the current uniformity.
To find out the influence of partial disordering on the current structure, simulation was carried out with random shifts at a level of 20% distortion of a lattice constant. The results of simulation are presented in Figure 6. The comparison of calculations with the pattern obtained with regular arrangement of individual sources has shown that 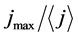 increases no more than by 1%, and
increases no more than by 1%, and 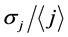 becomes only 0.3% more. Hence it follows that partial disordering of a regular structure retains general characteristics of degree of current nonuniformity.
becomes only 0.3% more. Hence it follows that partial disordering of a regular structure retains general characteristics of degree of current nonuniformity.
4. Conclusions
The investigation carried out has shown that it is convenient to describe propagation of electrons from a field carbon emitter on the basis of exact Green functions of the Schrödinger equation in a uniform electric field. Each protruding element of the carbon fiber end surface can be simulated by a point source of electron waves. The high nonuniformity of sources results in loss of coherence for different sources and in nonuniform density of electron
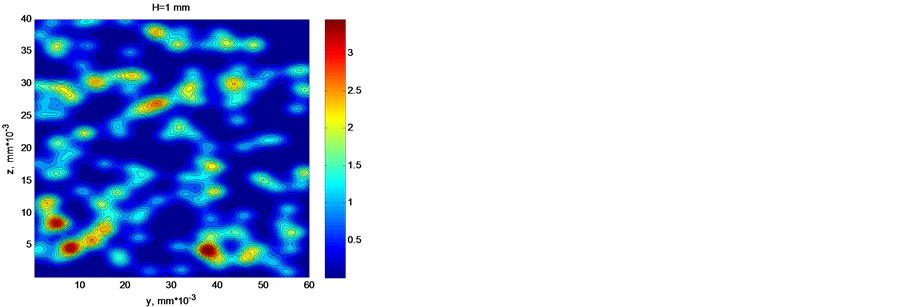
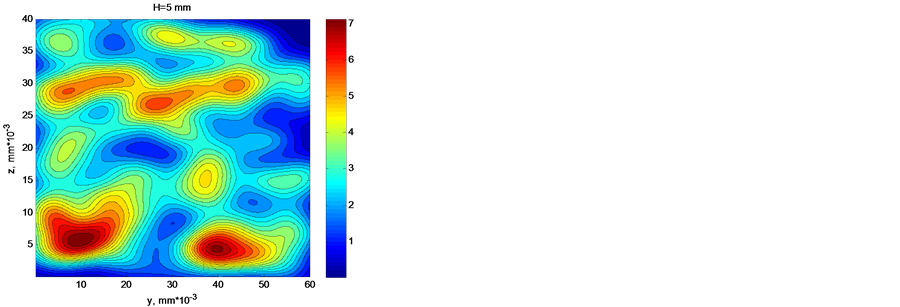
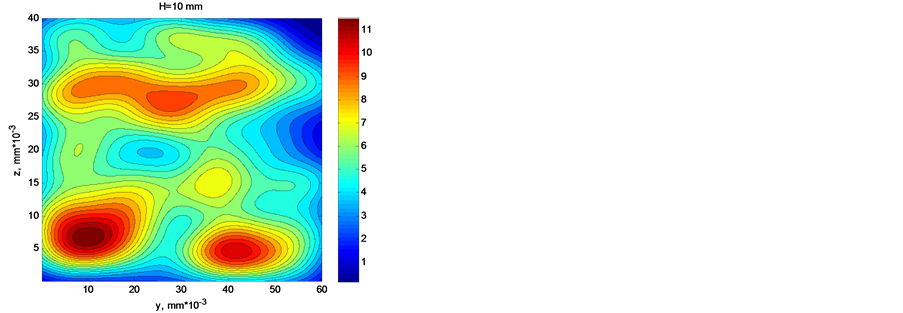

Figure 4. The shadowgraph of distribution of current from random sources.

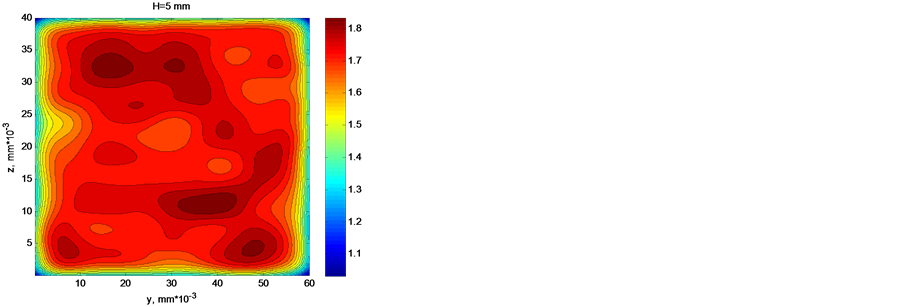
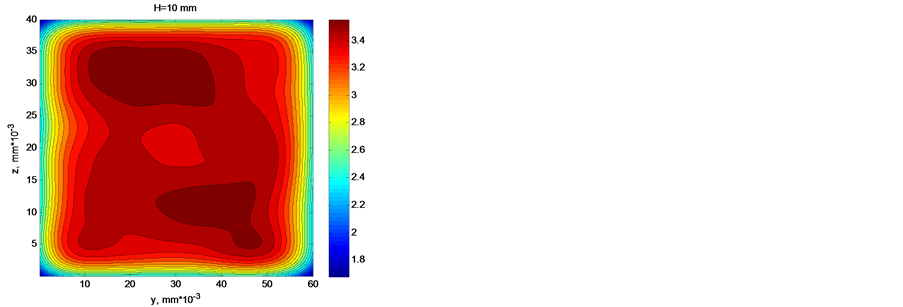
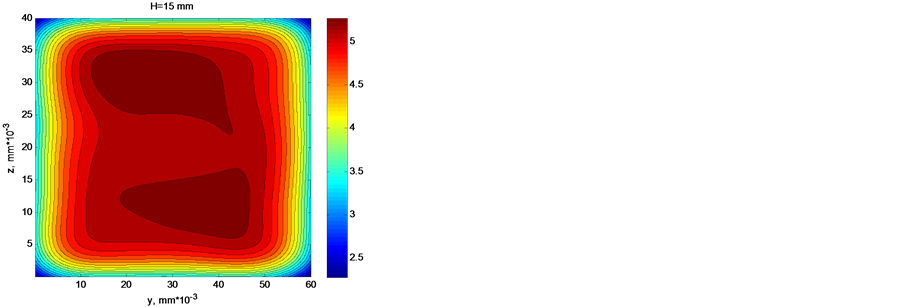
Figure 5. The shadowgraph of distribution of current from regularly arranged sources.
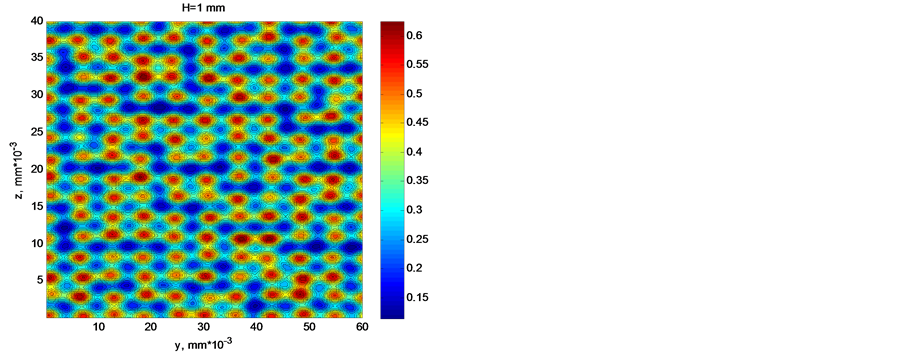


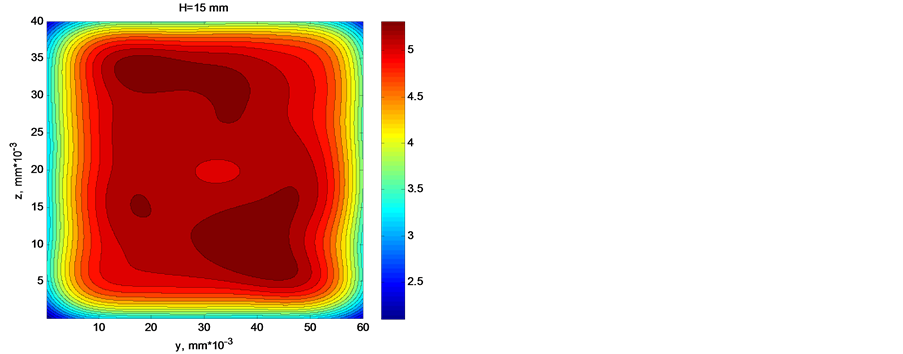
Figure 6. The shadow graph of distribution of current from regularly arranged sources in case of random shifts in their arrangement.
current distribution, and in calculations of field emission it is possible to sum densities of currents from individual sources.
Simulation by the Monte Carlo method allows obtaining characteristic patterns of current distribution for different densities of sources, field gains, and distances to the screen. Going from the random distribution of sources to their regular arrangement, even in case of partial loss of the order, considerably increases the current uniformity. The developed model allows choosing preferable parameters to increase the efficiency and life of radiation sources based on field carbon emitters.
Acknowledgements
The work has been done with the financial support of Russian Foundation for Basic Research (grant 13-07- 00270) and RF Government Contract No. 14.513.11.0133.
Conflict of Interest
The authors declare that there is no conflict of interests regarding the publication of this article.
REFERENCES
- P. Verma, S. Gautam, S. Pal, et al., “Carbon NanotubeBased Cold Cathode for High Power Microwave Vacuum Electronic Devices: A Potential Field Emitter,” Defence Science Journal, Vol. 58, No. 5, 2008, pp. 650-654.
- Y. Cheng and O. Zhou, “Electron Field Emission from Carbon Nanotubes,” Comptes Rendus Physique, Vol. 4, No. 9, 2003, pp. 1021-1033. http://dx.doi.org/10.1016/S1631-0705(03)00103-8
- H. S. Kim, D. Q. Duy, J. H. Kim, et al., “Field Emission Electron Source Using Carbon Nanotubes for X-Ray Tubes,” Journal of the Korean Physical Society, Vol. 52, 2008, pp. 1057-1060. http://dx.doi.org/10.3938/jkps.52.1057
- R. H. Fowler and L. Nordheim, “Electron Emission in Intense Electric Fields,” Proceedings of the Royal Society A, Vol. 119, 1928, pp. 173-181. http://dx.doi.org/10.1098/rspa.1928.0091
- P. Gröning, P. Ruffieux, L. Schlapbach, et al., “Carbon Nanotubes for Cold Electron Sources,” Advanced Engineering Materials, Vol. 5, No. 8, 2003, pp. 541-550. http://dx.doi.org/10.1002/adem.200310098
- S.-D. Liang and L. Chen, “Generalized Fowler-Northeim Theory of Field Emission of Carbon Nanotubes,” Physical Review Letters, Vol. 101, Vol. 4, 2008, Article ID: 027602.
- Ch. Adessi and M. Devel, “Theoretical Study of Field Emission by Single-Wall Curbon Nanonotubes,” Physical Review B, Vol. 62, No. 20, 2000, pp. R13314-13317. http://dx.doi.org/10.1103/PhysRevB.62.R13314
- A. B. Elitskii, “Carbon Nanotube-Based Electron Field Emitters,” Physics-Uspekhi, Vol. 53, No. 9, 2010, pp. 863-892. http://dx.doi.org/10.3367/UFNe.0180.201009a.0897
- G. B. Bocharov and A. V. Eletskii, “Theory of Carbon Nanotube (CNT)-Based Electron Field Emitters,” Nanomaterials, Vol. 3, 2013, pp. 393-442. http://dx.doi.org/10.3390/nano3030393
- Yu. N. Demkov and V. N. Ostrovsky, “Zero-Range Potentials and Their Application in Atomic Physics,” Plenum Press, New York, 1988.
- B. Gottlieb, M. Kleber and J. Krause, “Tunneling from a 3-Dimensional Quantum Well in an Electric Field: An Analytic Solution,” Zeitschrift für Physik A Hadrons and Nuclei, Vol. 339, No. 1, 1991, pp. 201-206. http://dx.doi.org/10.1007/BF01282950
- D. Gottlieb and M. Kleber, “Tunneling Dynamics in Stationary Field Emission,” Annalen der Physik, Vol. 504, No. 5, 1992, pp. 369-379. http://dx.doi.org/10.1002/andp.19925040507
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions,” National Bureau of Standards, Washington DC, 1972.
- Yu. N. Demkov and G. F. Drukarev, “Decay and the Polarizability of the Negative Ion in an Electric Field,” Soviet Physics JETP, Vol. 20, 1965, pp. 614-618.
- B. V. Bondarenko, Yu. L. Rybakov and E. P. Sheshin, “Field Emission of Carbon Fiber,” RE No. 8, Vol. 1593, 1982 (in Russian).
- E. P. Sheshin, “The Surface Structure and Field Emission Properties of Carbon Materials,” MIPT, Moscow, 2001.
- K. Cahill, “Physical Mathematics,” Cambridge University Press, Cambridge, 2013. http://dx.doi.org/10.1017/CBO9780511793738
- W. Feller, “An Introduction to Probability Theory and Its Applications,” Vol. 1, Wiley & Sons, New York, 1968.
- D. E. Knuth, “The Art of Computer Programming,” Vol. 2, Seminumerical Algorithms, Addison-Wesley Professional, Reading, 1981.

