Journal of Electromagnetic Analysis and Applications
Vol.06 No.04(2014), Article ID:43962,5 pages
10.4236/jemaa.2014.64008
Method of Images to Study the Charge Distribution in Cases of Potentials Deviating from Coulomb’s Law
Abdulwahab K. Sallabi*, Jamal A. Khaliel, Ali Sulaiman Mohamed
Department of Physics, Faculty of Science, Misurata University, Misurata, Libya
Email: *sallabiabdulwahab@yahoo.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 November 2013; revised 6 December 2013; accepted 5 January 2014
ABSTRACT
The method of images is used to study the charge distribution for cases where Coulomb’s law deviates from the inverse square law. This method shows that in these cases some of the charge goes to the surface, while the remainder charge distributed over the volume of the conductor. In accord with the experimental work, we show that the charge distribution will depend on the photon rest mass and is very sensitive to it; a very small value of the rest of mass of the photon will create deviation from Coulomb’s law.
Keywords:
Coulomb; Method of Images; Charge Distribution

1. Introduction
One of the foundations of electrostatics is Coulomb’s law. Major electromagnetic laws are built upon this law. As a direct consequence of this law (or its equivalent, Gauss’s law), any excess charge placed on a conductor must lie entirely on its surface. According to Coulomb’s law, excess charges given to a conductor will move away from each other and distribute themselves about the conductor in such a manner as to reduce the total amount of repulsive forces within the conductor and that both the charge and the field inside the conductor will vanish [1] -[6] .
Testing this law has been a subject for many experiments over the past two and a half centuries [1] [2] . Any deviation from inverse square law would suggest a finite range for electromagnetic force, implying a nonzero photon rest mass. Rest mass of the photon provides indirect test of the deviations from exactness of Coulomb’s law. If the photon mass is zero, Coulomb’s inverse-square law is the foundational law in electrostatics. Experiments measure deviations in the exponent of inverse-square law and photon rest mass are increasingly exact. The most recent ion interferometry experiment measures the value of the exponent to be a few times 10−22 and detect a photon rest mass at the level of 9 × 10−50 grams [1] . Detection of any deviation from Coulomb’s law would have far-reaching implications. Maxwell’s equations and much of the standard model would have to be modified. The notion that absolute electrostatic potential is arbitrary would have to be abandoned, along with many other tenets of classical electromagnetism [1] .
In an interesting papers, Spencer [3] and Griffiths and Uvanovic [4] studied distribution of excess charge within a conductor for laws rather than inverse square law such as Yukawa’s law or power law. In these two cases they found that some of the charge goes to the surface, and the remainder distributes itself uniformly over the volume of the conductor.
In this paper we introduce the method of images to study the distribution of charges in cases where the potential is depending on the photon rest of mass. And give a theoretical extension work to the experimental results that detect a photon rest mass at the level of 9 × 10−50 grams and as a result a deviating from Coulomb’s Law. This paper is also important to understand physics of molecules and electron transport through a single molecule which offers a highly promising new technology for the production of electronic chip.
2. Method and Results
2.1. Method of Images for Yukawa Potential and Grounded Spherical Conductor
The reaction field of a point charge due to surrounding medium can be represented by the method of image charge. The method of images allows us to solve certain differential form of electric potential problem without specifically solving a differential equation of this problem.
The potential 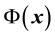 everywhere outside a conducting sphere can be calculated by using method of images. As illustrated Figure 1 we consider conducting sphere with radius
everywhere outside a conducting sphere can be calculated by using method of images. As illustrated Figure 1 we consider conducting sphere with radius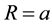 . For convenience, place the sphere at the origin. We assume a point charge
. For convenience, place the sphere at the origin. We assume a point charge 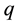 outside the sphere and defined by position vector
outside the sphere and defined by position vector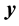 . By symmetry, the image charge lie on the line connecting the charge and the origin of the sphere and will be located inside the sphere at position vector
. By symmetry, the image charge lie on the line connecting the charge and the origin of the sphere and will be located inside the sphere at position vector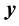 . If the sphere is grounded then the potential everywhere on the sphere equal zero. Now we are able to calculate the magnitude and the position vector
. If the sphere is grounded then the potential everywhere on the sphere equal zero. Now we are able to calculate the magnitude and the position vector 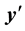 of an image charge
of an image charge 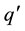 that is required to make the potential equal zero on the surface of the grounded sphere. Total Yukawa potential [4]
that is required to make the potential equal zero on the surface of the grounded sphere. Total Yukawa potential [4] 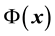 due to the assumed charge q and its image charge
due to the assumed charge q and its image charge 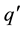 at any point P is given by Equation (1).
at any point P is given by Equation (1).
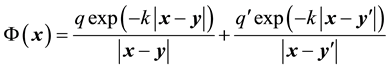 (1)
(1)
If the sphere is grounded, then the potential at the surface of the sphere vanishes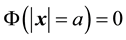 , thus:
, thus:
Figure 1. Two-dimensional schematic il- lustration of a conducting sphere of radius 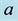 with a point charge
with a point charge 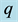 outside and image charge
outside and image charge 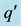 inside.
inside.
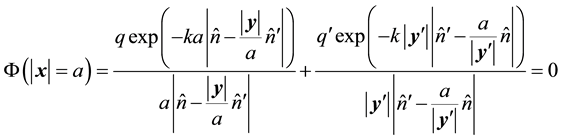 (2)
(2)
where 






More generally, the potential in the neighborhood of an uncharged grounded conducting sphere is given by Equation (4):

Let

Substitute Equation (5) in Equation (4) and then differentiate to get the actual induced charge density on the surface of the grounded uncharged conducting sphere:
Let
Then we get:

The total charge on the sphere may be found by integrating Equation (6) over all angles. The total surface induced charge is equal to the magnitude of the image charge for Coulomb potential. But in case of Yukawa potential the total surface induced charge is less than the value of the image charge. This result implies that small portion of the induced charge distributed itself inside the volume of the conducting sphere. The rest of the induced charge is distributed itself on the surface of the conducting sphere. Some values of the total induced surface charge on grounded conducting sphere are given in Table 1 for both Coulomb and Yuakawa potentials.
Table 1. Total induced surface charge normalized to 

2.2. Method of Images for Yukawa Potential and Insulated Charged Spherical Conductor
We can generalize Equation (4) for an insulated conducting sphere. Consider insulated charged sphere with total charge 






The surface charge density:


where

where
The charge density given by Equation (8) in units of 












3. Conclusion
In accord with the experimental work we show that the charge distribution greatly depends on the photon rest
Figure 2. The surface charge density normalized to 


Figure 3. The surface charge density normalized to 


Figure 4. The magnitude of the total surface charge normalized to 



mass and is very sensitive to it; a very small value of the rest of mass will create deviation from Coulomb’s law. We have studied the distribution of charges on grounded spherical conductor and insulated charged spherical conductor by using the method of images. It is proven that using the image charge to study the distribution of charges on conductors is effective. Our results show that the charge distribution is depending greatly on


References
- Neyenhuis, B., Christensen, D. and Durfee, D.S. (2007) Testing Nonclassical Theories of Electromagnetism with Ion Interferometry. Physical Review Letters, 99, 200401. http://dx.doi.org/10.1103/PhysRevLett.99.200401
- Tu, L.-C. and Lou, J. (2004) Experimental Tests of Coulomb’s Law and the Photon Rest Mass. Metrologia, 41, S136- S146.
- Spencer, R.L. (1990) If Coulomb’s Law Were Not Inverse Square: The Charge Distribution Inside a Solid Conducting Sphere. American Journal of Physics, 58, 385-390. http://dx.doi.org/10.1119/1.16179
- Griffiths, D.J. and Uvanovic, D.Z. (2001) The Charge Distribution on a Conductor for Non-Coulombic Potentials. American Journal of Physics, 69, 435-440. http://dx.doi.org/10.1119/1.1339279
- Jackson, J.D. (1975) Classical Electrodynamics. 2nd Edition, Wiley, New York.
- Griffiths, D.J. (1999) Introduction to Electrodynamics. 3rd Edition, Prentice-Hall, Upper Saddle River.
NOTES
*Corresponding author.












