Journal of Electromagnetic Analysis and Applications
Vol.4 No.2(2012), Article ID:17668,9 pages DOI:10.4236/jemaa.2012.42008
Far-Field Pattern Reconstruction from Positioning Errors Affected Near-Field Data Acquired via Helicoidal Scanning
![]()
Department of Electronic and Computer Engineering, University of Salerno, Fisciano, Italy.
Email: {fdagostino, flferrara, cgennarelli, rguerriero, mmigliozzi}@unisa.it
Received December 7th, 2011; revised January 10th, 2012; accepted January 19th, 2012
Keywords: Antenna Measurements; Near-Field - Far-Field Transformations; Helicoidal Scanning; Nonredundant Sampling Representations of Electromagnetic Fields; Probe Positioning Errors Compensation
ABSTRACT
In this paper, an effective technique to compensate the positioning errors in a near-field - far-field (NF-FF) transformation with helicoidal scanning for elongated antennas is presented and validated both numerically and experimentally. It relies on a nonredundant sampling representation of the voltage measured by the probe, obtained by considering the antenna as enclosed in a cylinder ended in two half-spheres. An iterative scheme is used to reconstruct the helicoidal NF data at the points fixed by the representation from the acquired irregularly spaced ones. Once the helicoidal data have been retrieved, those needed by a classical NF-FF transformation with cylindrical scanning are efficiently evaluated by using an optimal sampling interpolation algorithm. Some numerical tests, assessing the accuracy of the approach and its stability with respect to random errors affecting the data, are reported. Experimental tests performed at the Antenna Characterization Lab of the University of Salerno further confirm the validity of the proposed technique.
1. Introduction
Nowadays, the reduction of the time required to acquire the near-field data is assuming an ever growing relevance for the antenna measurement community. In fact, such a time is currently very much greater than that needed to perform the near-field - far-field (NF-FF) transformation. As suggested in [1], an effective way for reducing the measurement time is the use of innovative spiral scanning techniques [2-11], which can be implemented by means of continuous and synchronized movements of the positioning systems of the probe and antenna under test (AUT). These scans rely on the nonredundant sampling representations of electromagnetic (EM) fields [12] and use optimal sampling interpolation (OSI) formulas [13] to retrieve the NF data required by the NF-FF transformation with the corresponding classical scanning from the acquired nonredundant ones. Accordingly, a drastic measurement time saving can be achieved due to the use of continuous movements and to the significantly reduced number of acquired NF data. The resulting NF-FF transformations have proved to be accurate, stable, and efficient. In particular, the AUT has been considered as enclosed in the smallest sphere able to contain it in [2-5], whereas the unified theory of spiral scans for nonspherical antennas [11] has made possible to adopt more effective AUT modellings [6-10]. Besides a further reduction of the needed NF data in the case of elongated or quasiplanar antennas, these last allow one to consider measurement cylinders (planes) with a radius (distance) smaller than one half the antenna maximum size, thus reducing the error due to the scanning zone truncation.
It is worth noting that other spiral scanning techniques have been proposed [14,15], but since these last approaches do not exploit the nonredundant representations of EM fields, they need a useless large amount of NF measurements.
From a practical viewpoint, it may be impossible to get regularly distributed NF measurements due to an inaccurate control of the positioning systems. On the other hand, their position can be accurately read by optical devices. In addition, the finite resolution of the positioning systems does not allow one to exactly locate the probe at the points fixed by the sampling representation. Therefore, the development of an accurate and stable reconstruction process from irregularly spaced data becomes relevant. A procedure relying on the conjugate gradient iteration method and employing the unequally spaced fast Fourier transform (FFT) [16] has been applied in the standard planar [17] and spherical [18] scannings. However, such a procedure is unsuitable for scanning techniques based on the aforementioned nonredundant sampling representations, wherein proper OSI formulas are employed to retrieve the NF data required by the corresponding classical NF-FF transformation from the acquired nonredundant ones. In this context, the formulas available for the direct reconstruction from nonuniform samples are not user friendly, unstable, and valid only for particular sampling points arrangements [19]. A convenient policy is to recover the uniform samples from those irregularly spaced and then determine the value at any point of the scanning surface by an accurate and stable OSI formula. To this end, two different approaches have been proposed in [19,20] and compared and experimentally validated in the cylindrical scanning case [21]. The former [19] relies on an iterative technique which converges only if it is possible to build a biunique correspondence associating at each uniform sampling point the nearest nonuniform one. The latter [20] employs the singular value decomposition (SVD) method [22] and can be conveniently applied when the starting two-dimensional problem can be reduced to find the solution of two independent one-dimensional ones. If such a hypothesis is no longer valid, as in the helicodal scanning case, the dimension of the involved matrixes would become very large, thus requiring a massive computational effort. Accordingly, in order to compensate the positioning errors, the iterative technique has been successfully applied in [23,24] for reconstructing the uniformly distributed helicoidal samples from the acquired irregularly spaced ones in the NF-FF transformation with helicoidal scan for a quasi-spherical [2,5] and an elongated antenna [6,8], respectively.
The aim of this paper is to present and validate, both numerically and experimentally, the iterative scheme for compensating the positioning errors in the NF-FF transformation with helicoidal scanning for long antennas [7]. This last transformation assumes the AUT as enclosed in a cylinder ended in two half-spheres and, due to the flexibility of such a modelling, results to be more effective from the data reduction viewpoint than the one [6,8] employing the prolate ellipsoid.
2. Theoretical Background
For reader’s convenience the key steps of the classical probe compensated NF-FF transformation with cylindrical scanning [25], as well as those concerning the reconstruction of the probe voltage from a nonredundant number of its samples lying along a helix [7], are summarized in this Section.
2.1. Classical NF-FF Transformation with Cylindrical Scanning
Let us consider a probe scanning a cylinder of radius d in the antenna NF region, and adopt the spherical coordinate system (r, J, j) to denote an observation point both in the NF and in the FF region (see Figure 1).
According to the classical probe compensated NF-FF transformation with cylindrical scanning, the modal coefficients 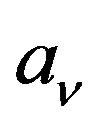 and
and 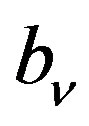 of the cylindrical wave expansion of the field radiated by the AUT are related to: 1) the two-dimensional Fourier transforms
of the cylindrical wave expansion of the field radiated by the AUT are related to: 1) the two-dimensional Fourier transforms 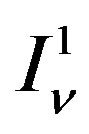 and
and  of the output voltages of the probe for two independent sets of measurements (the probe is rotated 90˚ about its longitudinal axis in the second set); 2) the coefficients (
of the output voltages of the probe for two independent sets of measurements (the probe is rotated 90˚ about its longitudinal axis in the second set); 2) the coefficients (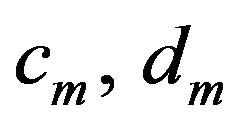 ) and (
) and (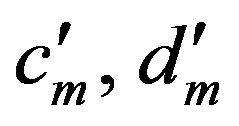 ) of the cylindrical wave expansion of the field radiated by the probe and the rotated probe, respectively, when used as transmitting antennas. The key relations [25] are:
) of the cylindrical wave expansion of the field radiated by the probe and the rotated probe, respectively, when used as transmitting antennas. The key relations [25] are:
 (1)
(1)
 (2)
(2)
 (3)
(3)
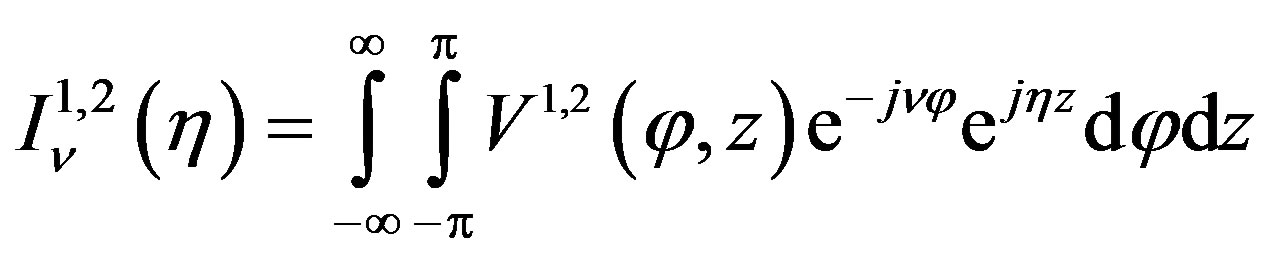 (4)
(4)
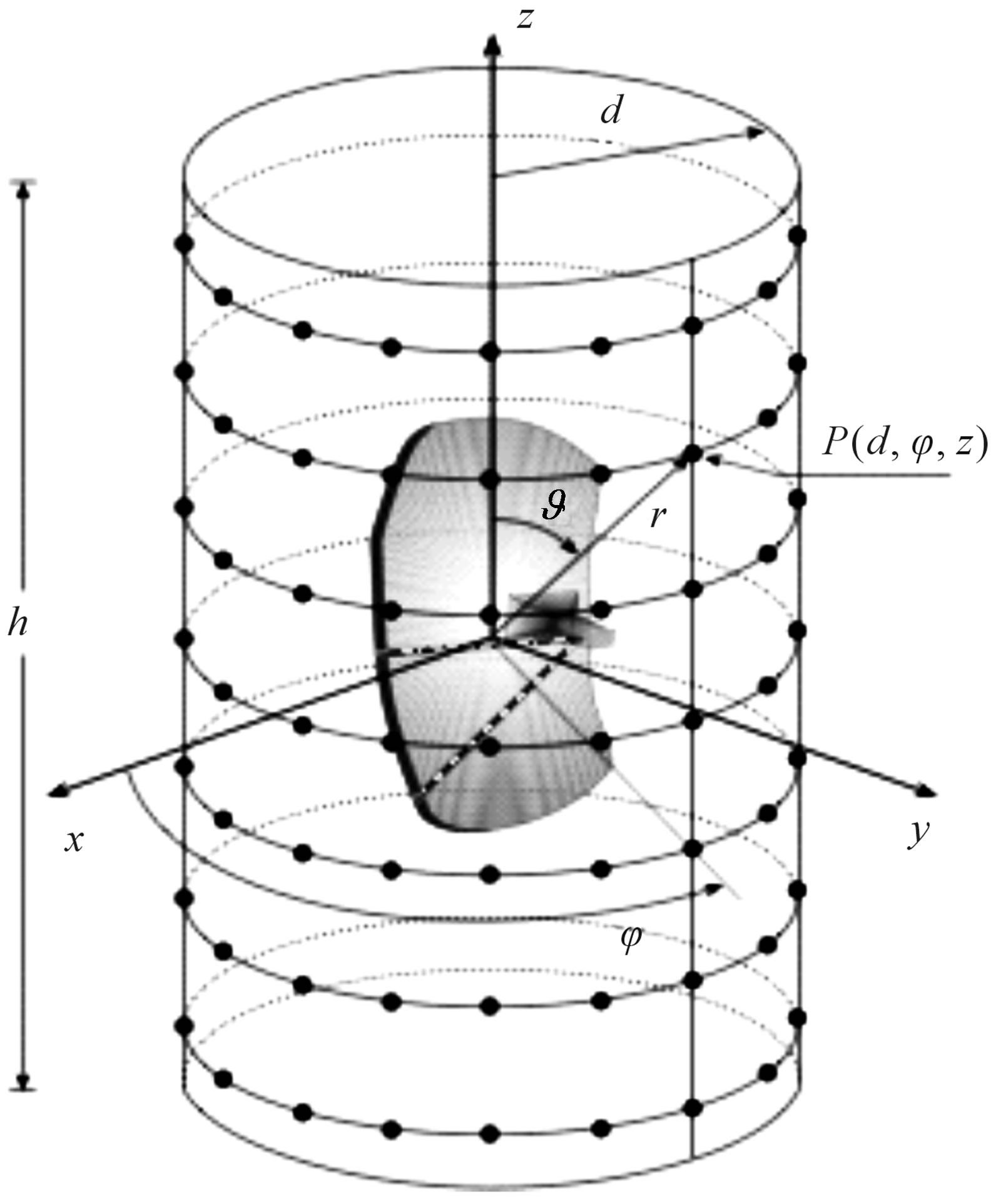
Figure 1. Cylindrical scanning.
wherein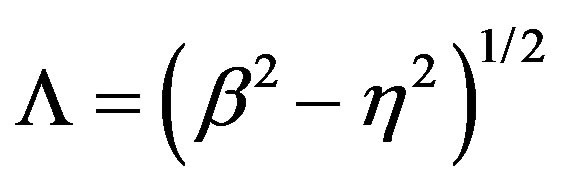 ,
, 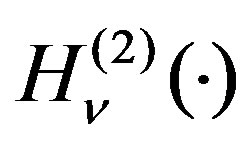 is the Hankel function of second kind and order n, b is the wavenumber, and
is the Hankel function of second kind and order n, b is the wavenumber, and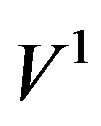 ,
, 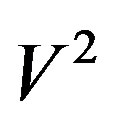 are the output voltages of the probe and the rotated probe at the point of cylindrical coordinates
are the output voltages of the probe and the rotated probe at the point of cylindrical coordinates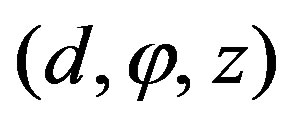 .
.
In the classical approach [25], the FFT is employed to evaluate in an efficient way the Fourier transforms (4), and the NF data are collected on a cylindrical grid wherein the sample spacing Dz between the rings is smaller than one half a wavelength and the one Dj on each of them is fixed according to the so called minimum cylinder law, i.e.,
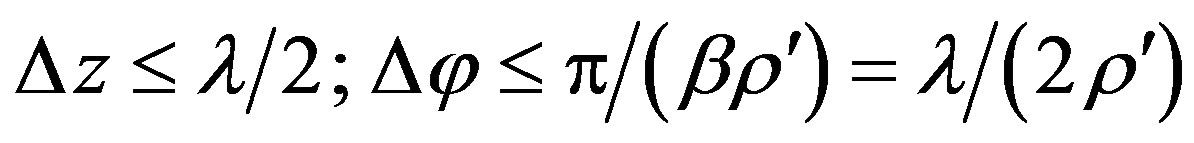 (5)
(5)
where r' is the radius of the smallest cylinder enclosing the AUT and l is the wavelength.
Once the modal coefficients have been determined, the FF components of the electric field can be evaluated by means of the following relations:
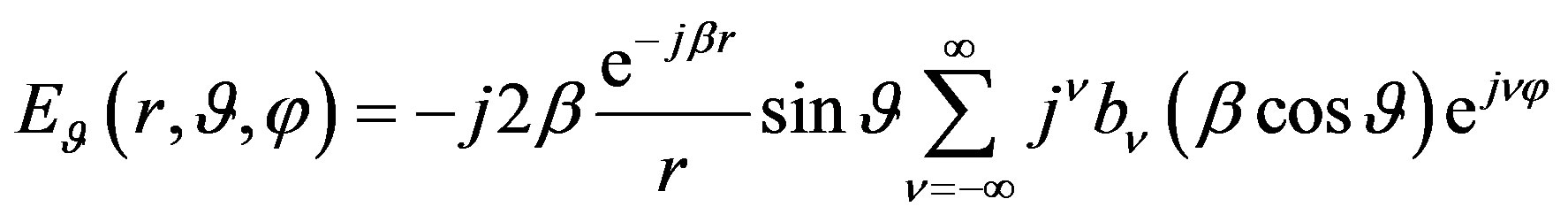 (6)
(6)
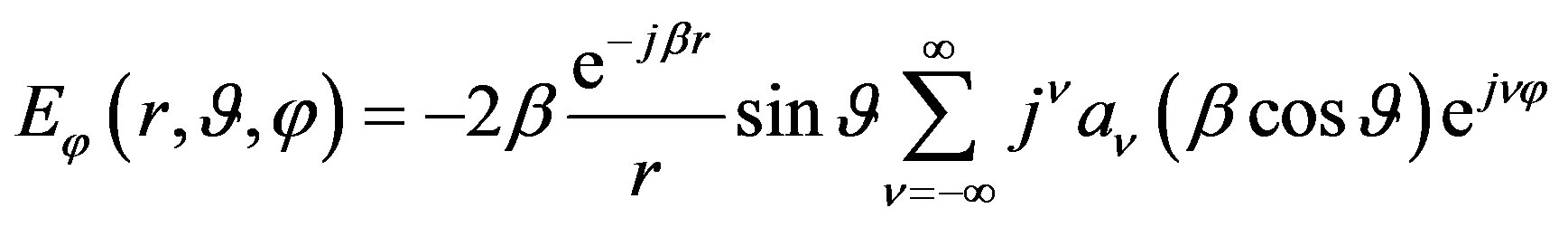 (7)
(7)
which can be efficiently computed by performing the summations via the FFT algorithm.
In the next subsection, it is shown how the NF data at the grid spacings (5) can be recovered from a nonredundant (i.e. minimum) number of samples collected by the probe and rotated probe along a helix wrapping the measurement cylinder [7].
2.2. Nonredundant Sampling Representation on a Cylinder
Let us consider an elongated AUT, enclosed in a convex domain bounded by a surface S with rotational symmetry, and a nondirective probe scanning a proper helix lying on a cylinder of radius d (Figure 2). A shape suitable to fit such an AUT is obtained by choosing S coincident with a rounded cylinder, namely, a cylinder of height  ended in two half-spheres of radius
ended in two half-spheres of radius  (see Figure 2). Since the voltage measured by a nondirective probe has the same effective spatial bandwidth of the AUT field [26], the nonredundant representations of EM fields [12] can be applied to it. Accordingly, when dealing with the representation of the probe voltage on an observation curve C, it is convenient to adopt an optimal analytical parameterization r = r(h) to describe C and to introduce the “reduced voltage”
(see Figure 2). Since the voltage measured by a nondirective probe has the same effective spatial bandwidth of the AUT field [26], the nonredundant representations of EM fields [12] can be applied to it. Accordingly, when dealing with the representation of the probe voltage on an observation curve C, it is convenient to adopt an optimal analytical parameterization r = r(h) to describe C and to introduce the “reduced voltage”
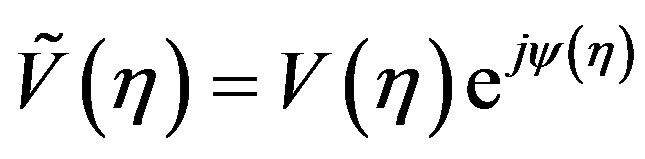 (8)
(8)
where  is the voltage measured by the probe or by
is the voltage measured by the probe or by

Figure 2. Geometry of the problem.
the rotated probe, and 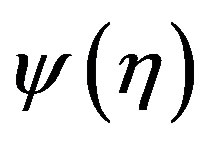 is a proper phase function. The error, occurring when
is a proper phase function. The error, occurring when  is approximated by a bandlimited function, becomes negligible as the bandwidth exceeds a critical value
is approximated by a bandlimited function, becomes negligible as the bandwidth exceeds a critical value 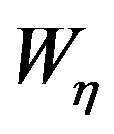 [12]. Therefore, it can be effectively controlled by choosing a bandwidth equal to
[12]. Therefore, it can be effectively controlled by choosing a bandwidth equal to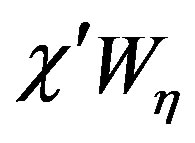 , where
, where 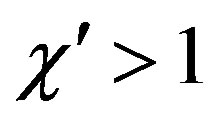 is the bandwidth enlargement factor.
is the bandwidth enlargement factor.
The unified theory of spiral scans for nonspherical antennas [11] allows the development of the voltage representation on the cylinder from a nonredundant number of its samples on the helix. To this end, it is necessary: 1) to determine a nonredundant representation along the helix; 2) to choose the step of the helix coincident with that required for the interpolation along a generatrix. In particular, according to [7,11], the bandwidth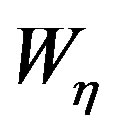 , the parameterization h and the phase function y relevant to a generatrix are:
, the parameterization h and the phase function y relevant to a generatrix are:
 (9)
(9)
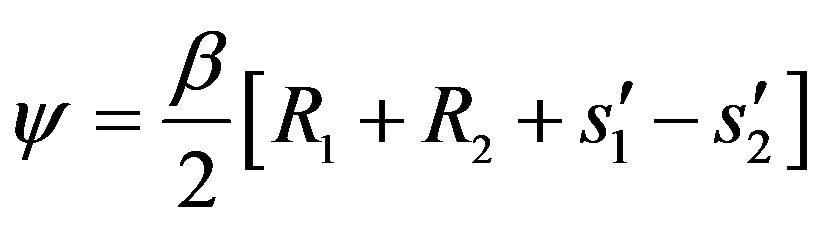 (10)
(10)
where 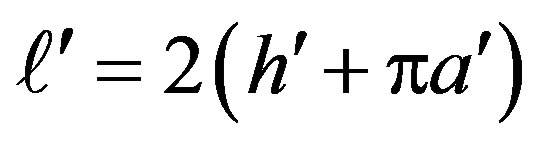 is the length of
is the length of  (intersection curve between the meridian plane and S),
(intersection curve between the meridian plane and S),  are the arclength coordinates of the tangency points
are the arclength coordinates of the tangency points 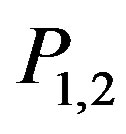 between the cone of vertex at the observation point P and
between the cone of vertex at the observation point P and , and
, and
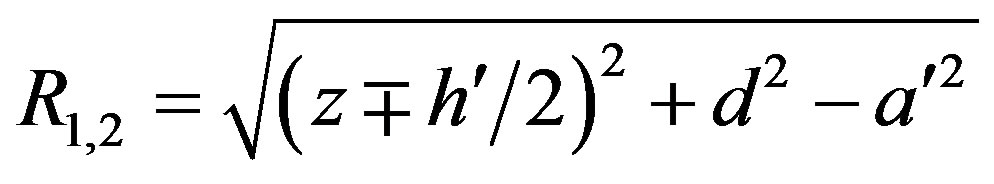 (11)
(11)
are the distances from P to  (see Figure 3). It can be easily verified that:
(see Figure 3). It can be easily verified that:
 (12)
(12)
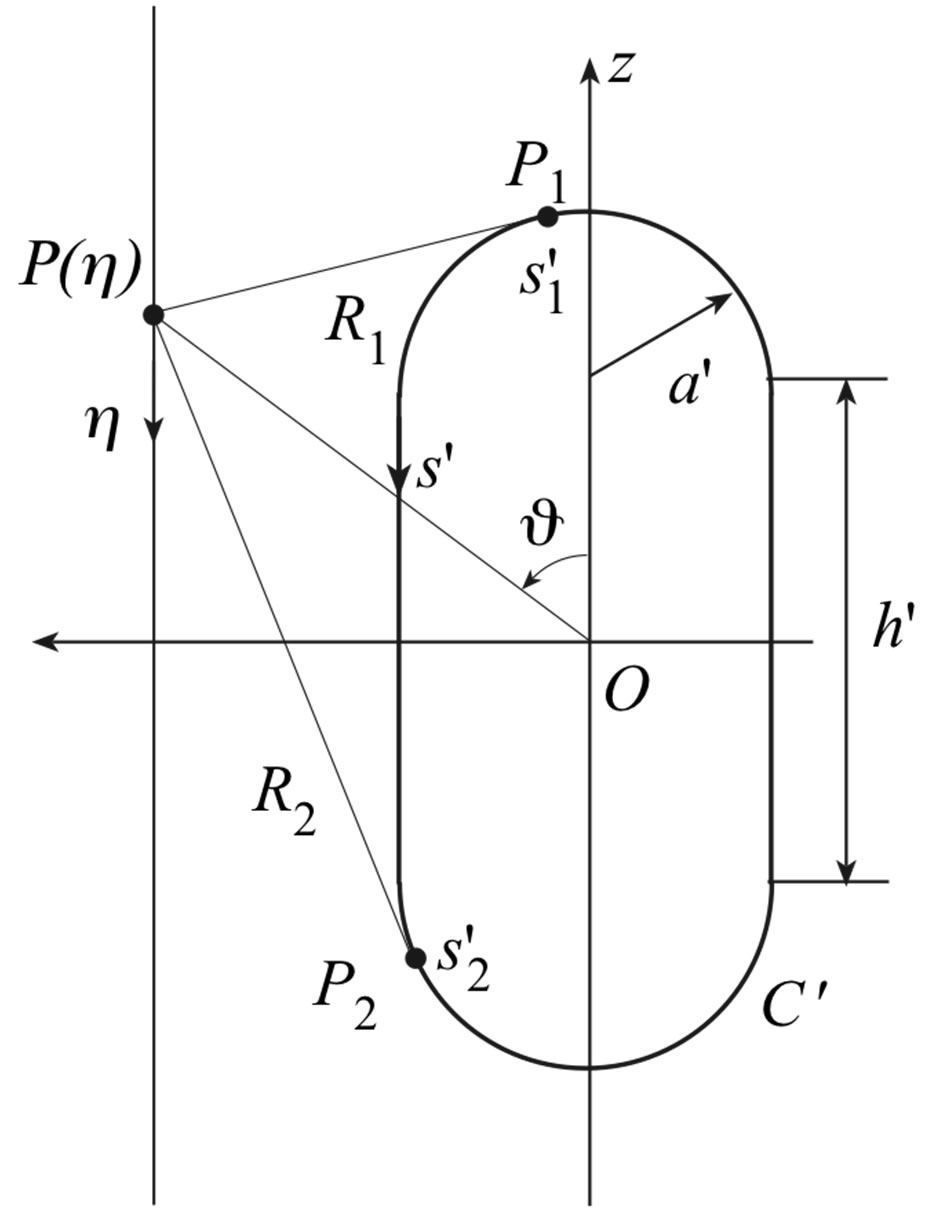
Figure 3. Relevant to a generatrix.
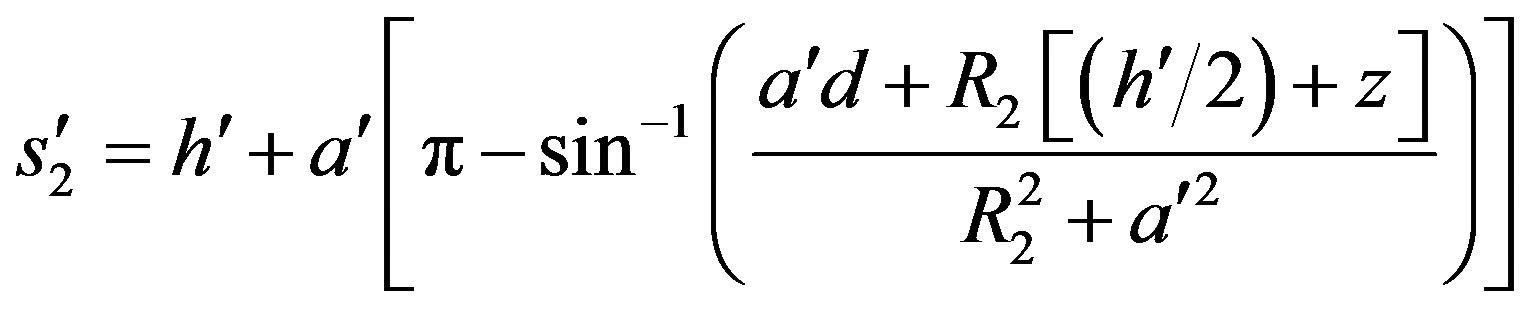 (13)
(13)
The helix is obtained by projecting onto the scanning cylinder a proper spiral wrapping S. The projection is obtained via the curves at h = const [7,11]. The helix step, determined by two consecutive intersections with a given generatrix, is equal to the sample spacing 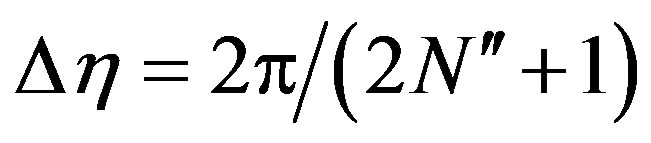 required to interpolate the voltage along a generatrix. Note that
required to interpolate the voltage along a generatrix. Note that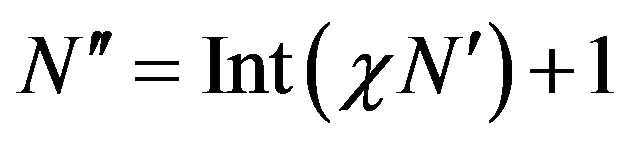 , where Int(x) denotes the integer part of x,
, where Int(x) denotes the integer part of x, 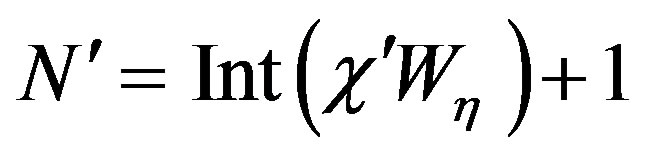 , and
, and 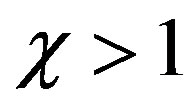 is an oversampling factor that controls the truncation error [13]. The equations of the helix, when imposing its passage through a fixed point
is an oversampling factor that controls the truncation error [13]. The equations of the helix, when imposing its passage through a fixed point 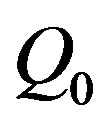 of the generatrix at j = 0, are:
of the generatrix at j = 0, are:
 (14)
(14)
wherein f is the parameter describing the helix,  is the value of f at
is the value of f at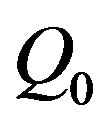 , and
, and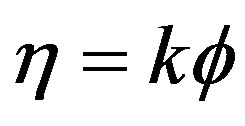 , k being a parameter related to the helix step by
, k being a parameter related to the helix step by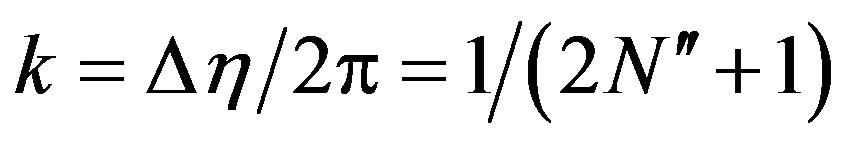 . A nonredundant representation along the helix is then obtained by enforcing the optimal parameter x for describing it equal to
. A nonredundant representation along the helix is then obtained by enforcing the optimal parameter x for describing it equal to 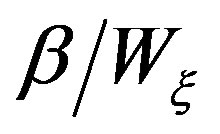 times the arclength of the projecting point on the spiral wrapping S and by choosing the related phase function g coincident with that y relevant to a generatrix. Moreover, the bandwidth
times the arclength of the projecting point on the spiral wrapping S and by choosing the related phase function g coincident with that y relevant to a generatrix. Moreover, the bandwidth  is chosen equal to
is chosen equal to 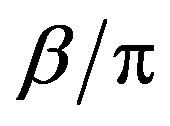 times the length of the spiral wrapping S from pole to pole [7].
times the length of the spiral wrapping S from pole to pole [7].
By exploiting the above results, the reduced voltage at any point of the helix can be recovered [7] via the OSI expansion:
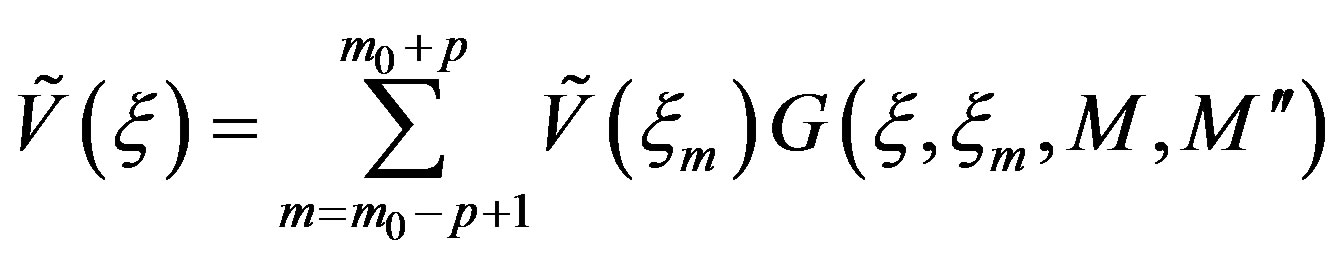 (15)
(15)
where  is the index of the sample nearest to the output point, 2p the number of retained samples
is the index of the sample nearest to the output point, 2p the number of retained samples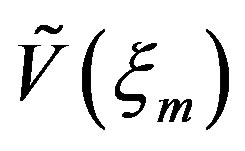 , and
, and
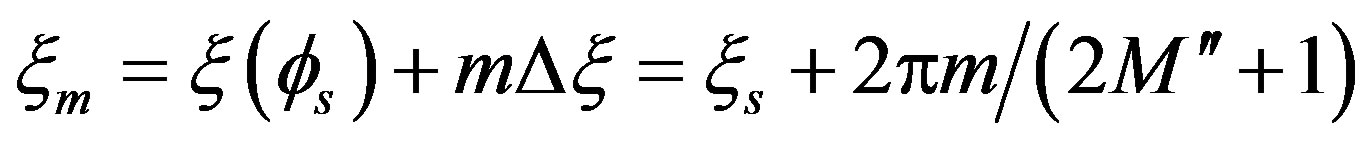 (16)
(16)
with 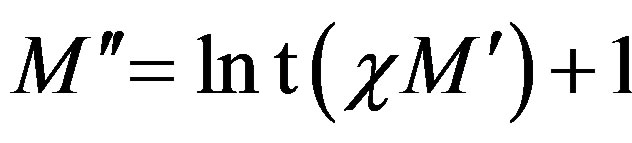 and
and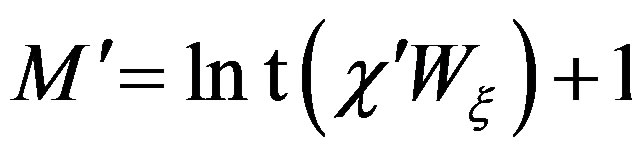 . Moreover,
. Moreover,
 (17)
(17)
wherein
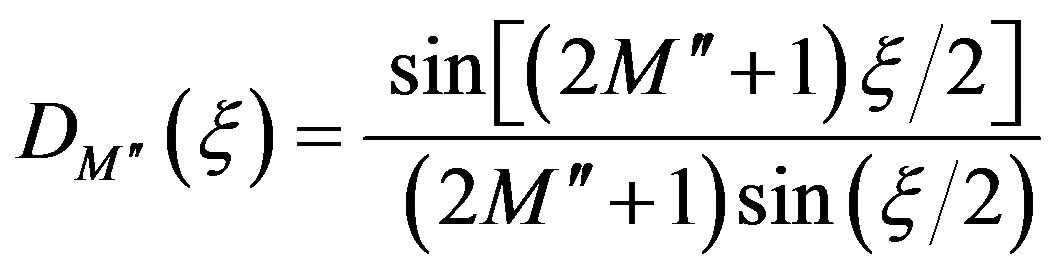 (18)
(18)
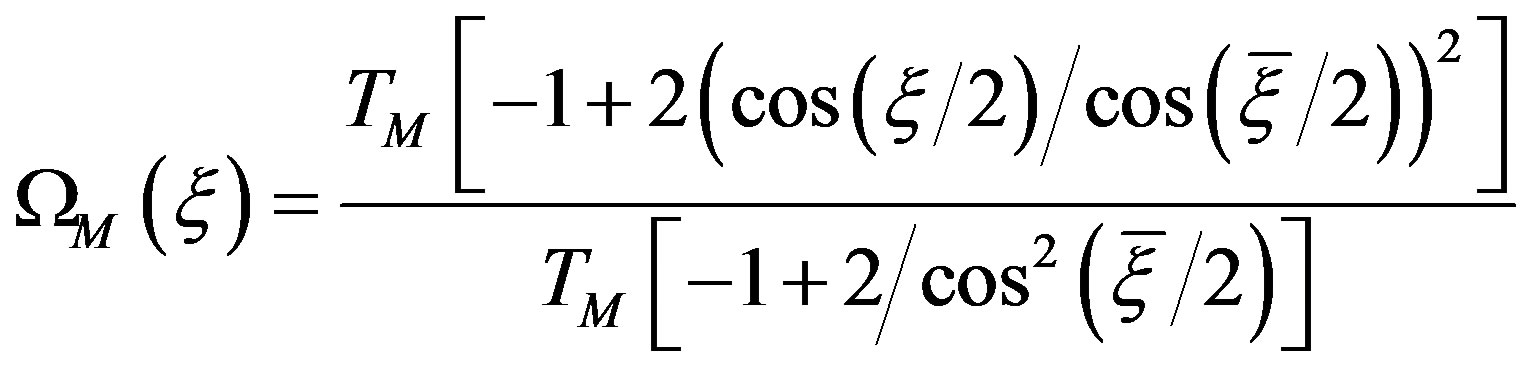 (19)
(19)
are the Dirichlet and Tschebyscheff sampling functions, respectively, 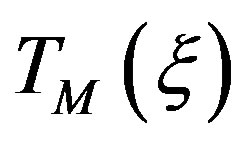 being the Tschebyscheff polynomial of degree
being the Tschebyscheff polynomial of degree 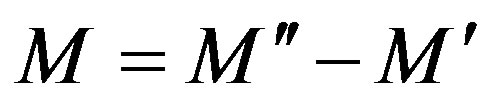 and
and .
.
The OSI expansion (15) can be applied to evaluate the “intermediate samples”, namely, the reduced voltage values at the intersection points between the helix and the generatrix passing through the observation point P. Once these samples have been determined, the reduced voltage at P can be evaluated by using a quite similar formula [7]. The following two-dimensional OSI expansion thus results:
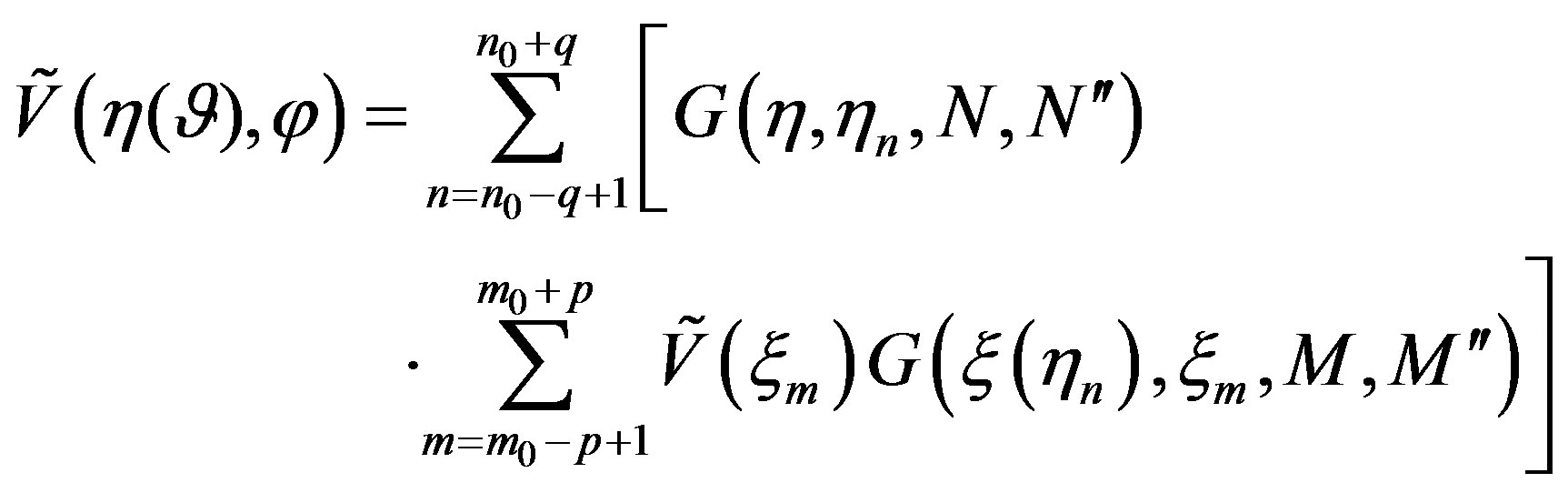 (20)
(20)
where , 2q is the number of the retained intermediate samples
, 2q is the number of the retained intermediate samples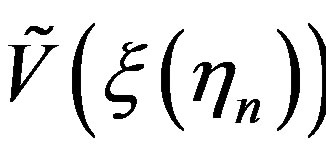 ,
,  ,
,
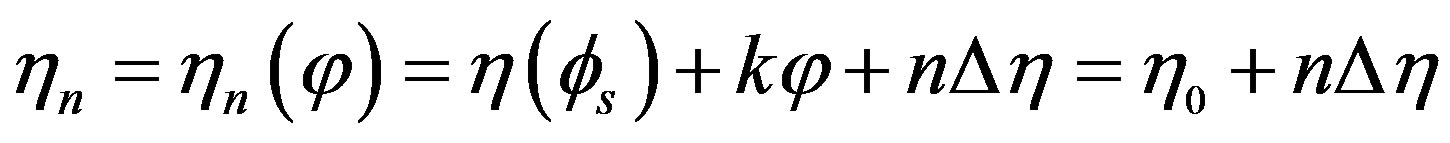 (21)
(21)
and the other symbols have the same meaning as in (15). Expansion (20) can be used to evaluate the voltage at any point P on the cylinder and, in particular, at those needed to perform the classical NF-FF transformation with cylindrical scanning [25].
3. Recovery of the Helicoidal Samples
Let us now turn to the case of irregularly spaced samples (Figure 2) and denote with 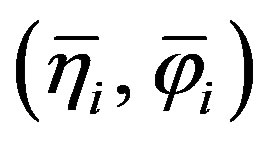 the nonuniform sampling point corresponding to the nearest uniform one
the nonuniform sampling point corresponding to the nearest uniform one 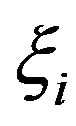 on the helix. By expressing the reduced voltage at each nonuniform sampling point as function of the unknown values at the nearest uniform ones via the OSI expansion (20) and neglecting the truncation errors, we get:
on the helix. By expressing the reduced voltage at each nonuniform sampling point as function of the unknown values at the nearest uniform ones via the OSI expansion (20) and neglecting the truncation errors, we get:
 (22)
(22)
where Q is the overall number of sampling points. Such a linear system can be rewritten in the matrix form
 , where
, where  is the
is the 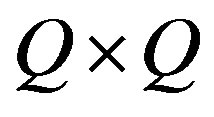 sparse matrix whose elements are
sparse matrix whose elements are
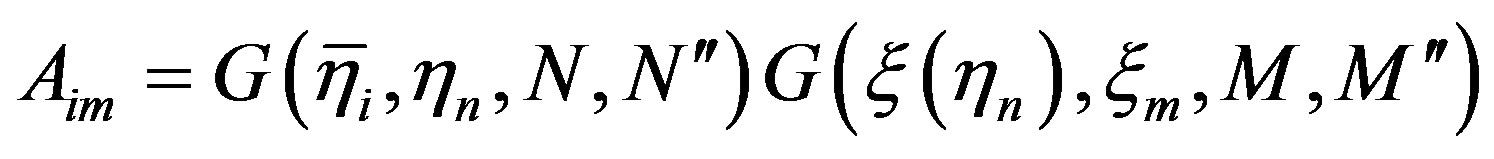 (23)
(23)
b is the vector of the collected nonuniform data, and x is the vector of the unknown uniform helicoidal samples.
By splitting 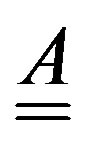 into its diagonal part
into its diagonal part 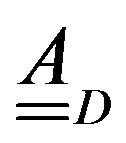 and nondiagonal one
and nondiagonal one , it results
, it results
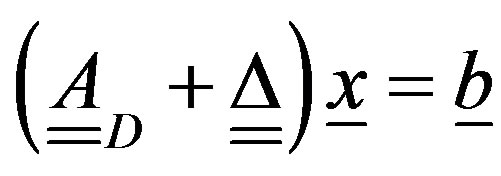 (24)
(24)
multiplying both members of (24) by 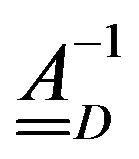 and rearranging the terms, we get
and rearranging the terms, we get
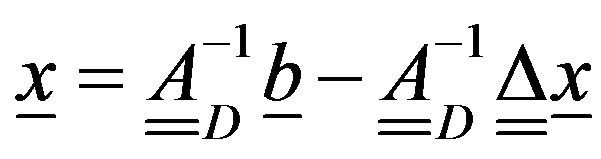 (25)
(25)
The following iterative procedure thus results
 (26)
(26)
where  is the vector of the uniform helicoidal samples estimated at the
is the vector of the uniform helicoidal samples estimated at the  step. Necessary conditions for the convergence [19] are that
step. Necessary conditions for the convergence [19] are that 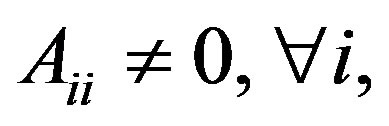 and
and 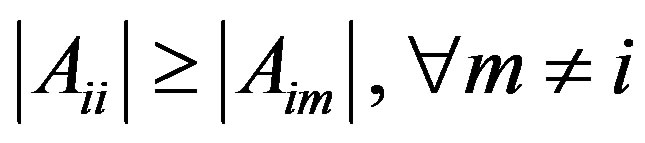 . These conditions are certainly satisfied in the here assumed hypothesis of one-to-one correspondence between each uniform helicoidal sampling point and the “nearest” nonuniform one. By straightforward evaluations, we finally get:
. These conditions are certainly satisfied in the here assumed hypothesis of one-to-one correspondence between each uniform helicoidal sampling point and the “nearest” nonuniform one. By straightforward evaluations, we finally get:
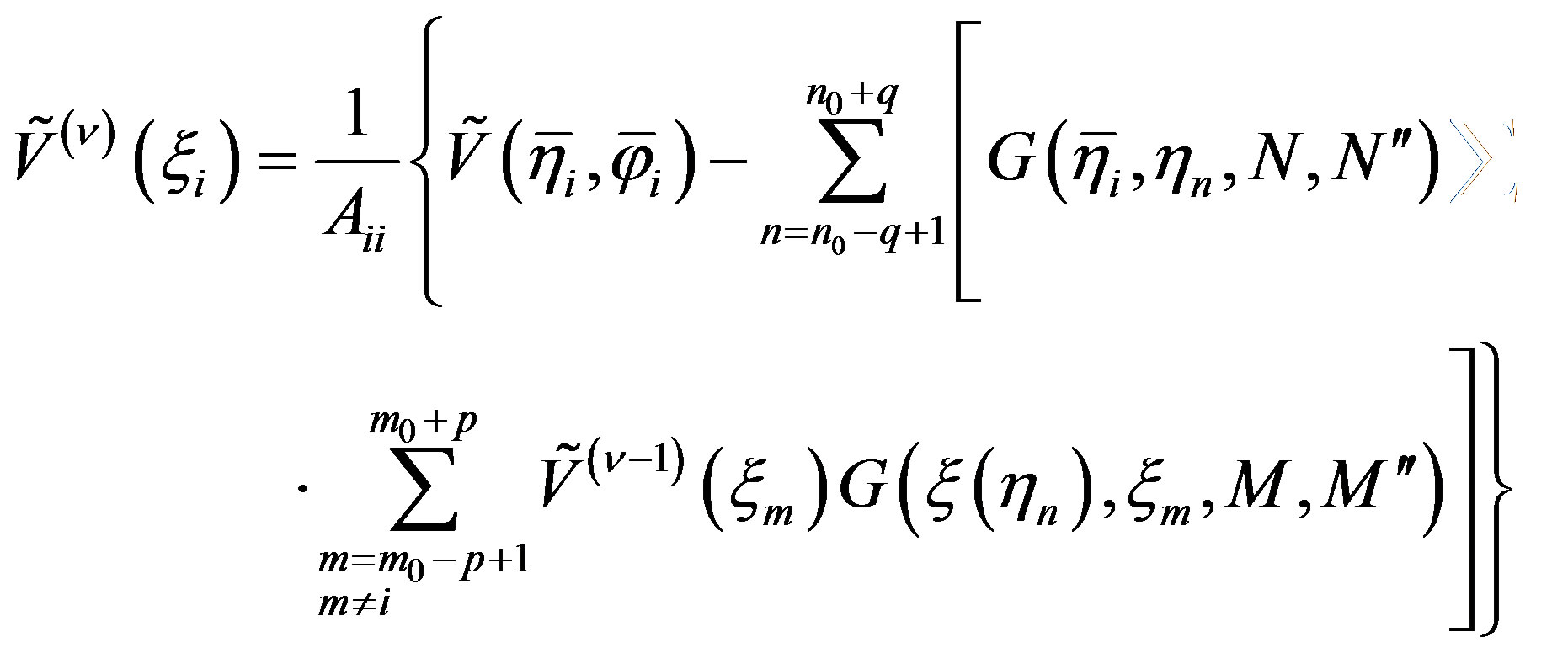 (27)
(27)
wherein
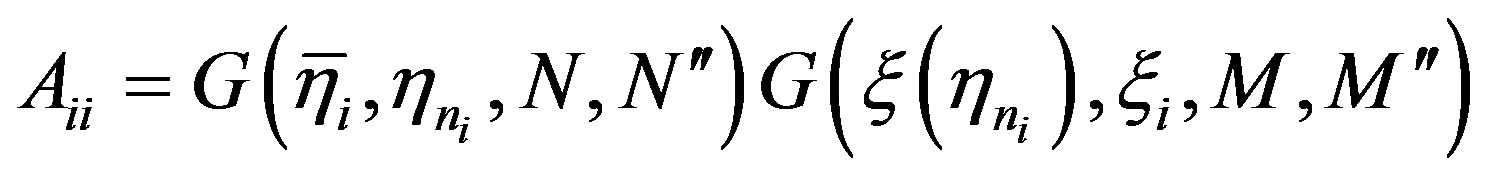 (28)
(28)
 being the index of the intermediate sampling point nearest to the uniform one
being the index of the intermediate sampling point nearest to the uniform one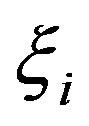 .
.
4. Numerical Simulations
The numerical simulations refer to a uniform planar array of 0.6l spaced elementary Huygens sources, polarized along the z axis and covering a zone in the plane y = 0, formed by a rectangle ended in two half-circles (see Figure 2). The rectangle sizes are: 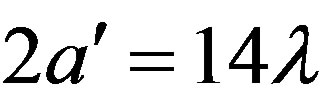 and
and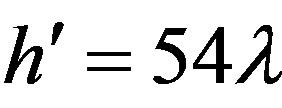 . The helix wraps a cylinder having radius
. The helix wraps a cylinder having radius  and height
and height  An open-ended WR-90 rectangular waveguide, at the frequency of 10 GHz, is chosen as probe. The nonuniform samples have been generated by imposing that the distances in x and h between the position of each nonuniform sample and the associate uniform one on the helix are random variables uniformly distributed in
An open-ended WR-90 rectangular waveguide, at the frequency of 10 GHz, is chosen as probe. The nonuniform samples have been generated by imposing that the distances in x and h between the position of each nonuniform sample and the associate uniform one on the helix are random variables uniformly distributed in 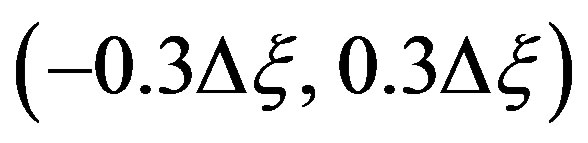 and
and 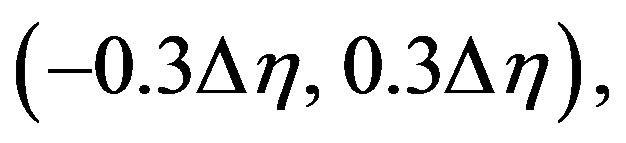 which represents a pessimistic occurrence in a real scanning procedure.
which represents a pessimistic occurrence in a real scanning procedure.
A reconstruction example of the voltage V1 (the most significant one) on the generatrix at j = 90˚, obtained by 0 and 6 iterations, is shown in Figures 4 and 5, respectively. As can be seen, 6 iterations are enough to get a very good recovery. The evaluation of the mean-square errors (normalized to the voltage maximum on the cylinder) in the reconstruction of the uniform samples assesses more quantitatively the effectiveness of the technique. They have been determined by comparing the reconstructed helicoidal samples and the exact ones in the central zone of the scanning surface, to assure the existence of the guard samples. As can be seen (Figure 6), on increasing the number of iterations, the errors decrease quickly until a constant saturation value is attained. This value decreases on increasing the number of retained samples. Even smaller errors are to be expected when the nonuniform samples are nearer to the uniform ones. The stability of the approach has been assessed (Figure 7) by corrupting the exact samples with random errors. Both a background noise (bounded to Da in amplitude and with arbitrary phase) and uncertainties on the data of 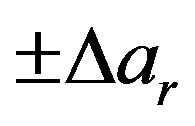 in amplitude and ±Da in phase have been simulated. The reconstructions of the FF pattern in the
in amplitude and ±Da in phase have been simulated. The reconstructions of the FF pattern in the
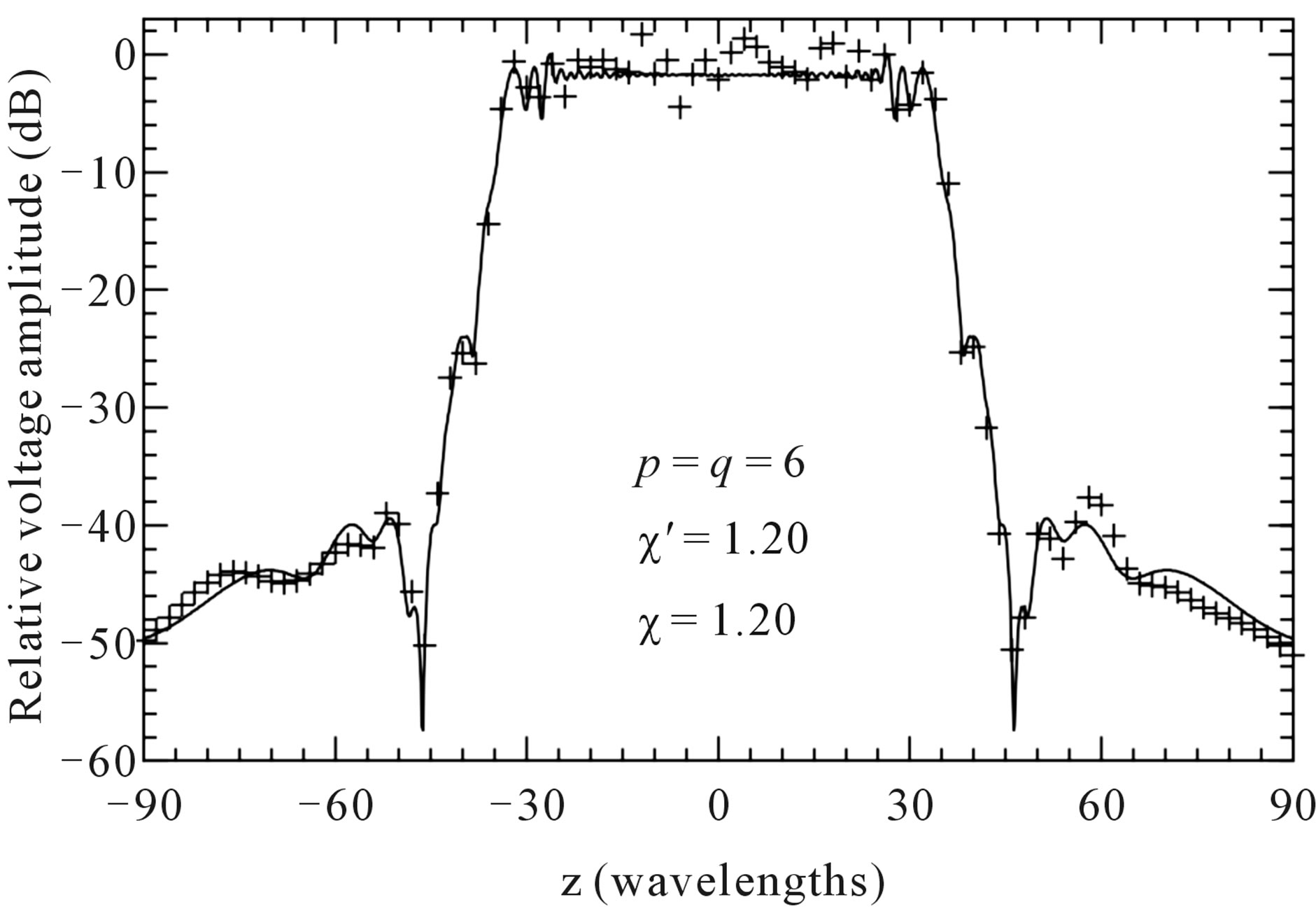
Figure 4. Amplitude of the probe voltage on the generatrix at φ = 90˚. Solid line: exact. Crosses: recovered at the iteration 0.

Figure 5. Amplitude of the probe voltage on the generatrix at φ = 90˚. Solid line: exact. Crosses: recovered at the iteration 6.

Figure 6. Normalized mean-square errors in the reconstruction of the uniform samples.
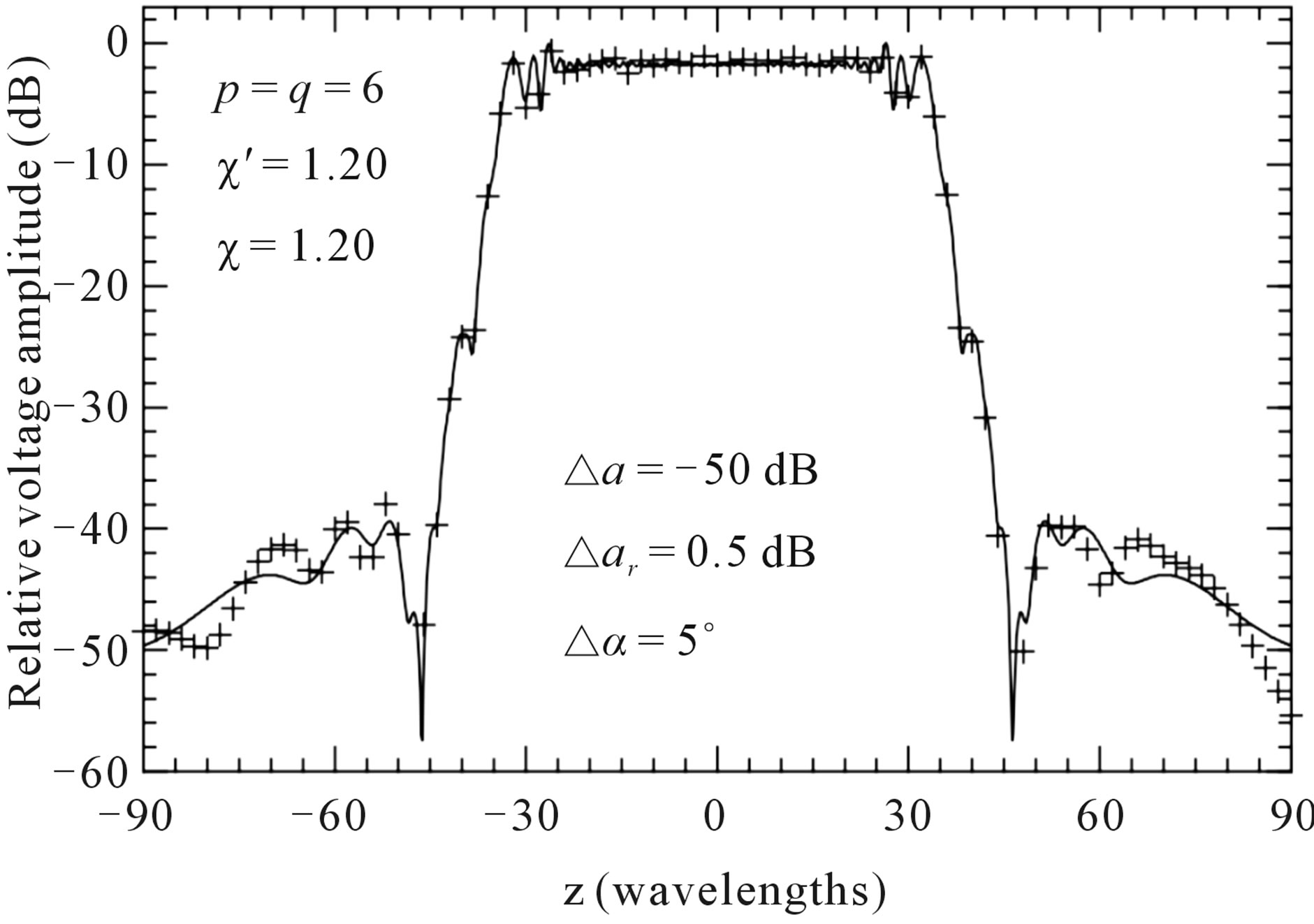
Figure 7. Amplitude of the probe voltage on the generatrix at φ = 90˚. Solid line: exact. Crosses: recovered at the iteration 6 from error affected data.
principal planes are shown in Figures 8 and 9. As can be seen, the exact and recovered fields are indistinguishable, thus providing an overall assessment of the technique.
Note that the number of used samples for reconstructing the NF data over the considered cylinder is 29,260, about one half than that (46,080) needed by the standard cylindrical scanning and by the helicoidal scanning technique [14].
5. Experimental Validation
The described technique has been experimentally validated in the anechoic chamber available at the UNISA Antenna Characterization Lab. The chamber, whose dimensions are 8 m × 5 m × 4 m, is equipped with an advanced cylindrical NF facility supplied by MI Technologies. An open-ended WR90 rectangular waveguide is used as probe. The AUT, located in the plane x = 0, is a very simple H-plane monopulse antenna, operating at 10 GHz in the sum mode. It has been realized by using two pyramidal horns (8.9 × 6.8 cm) made by Lectronic Research Labs at a distance of 26 cm (between centers) and a hybrid Tee (Figure 10). According to the described sampling representation, the AUT has been modelled as enclosed in a rounded cylinder having h' = 36 cm and
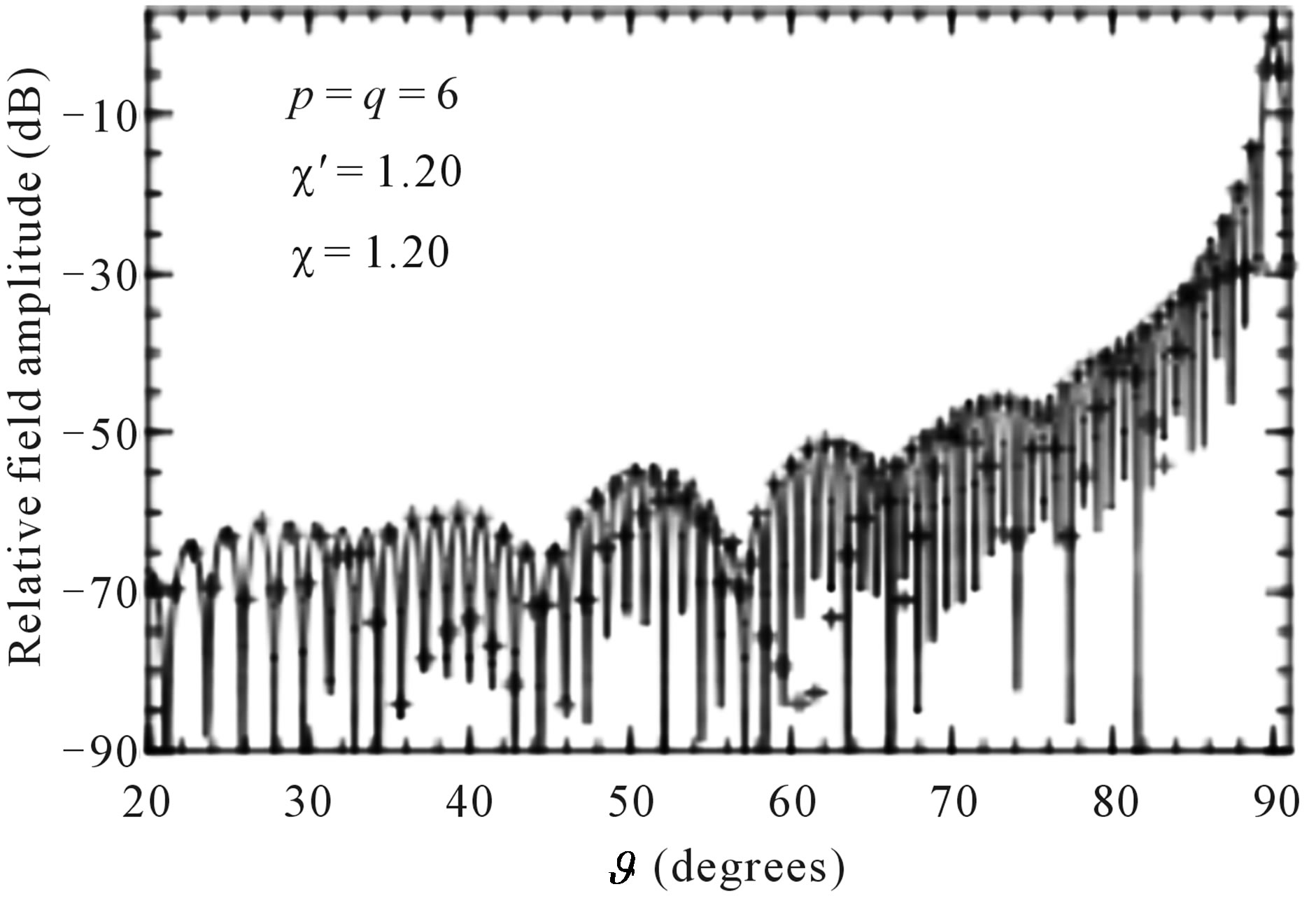
Figure 8. E-plane pattern. Solid line: exact. Crosses: reconstructed from nonuniform NF data.
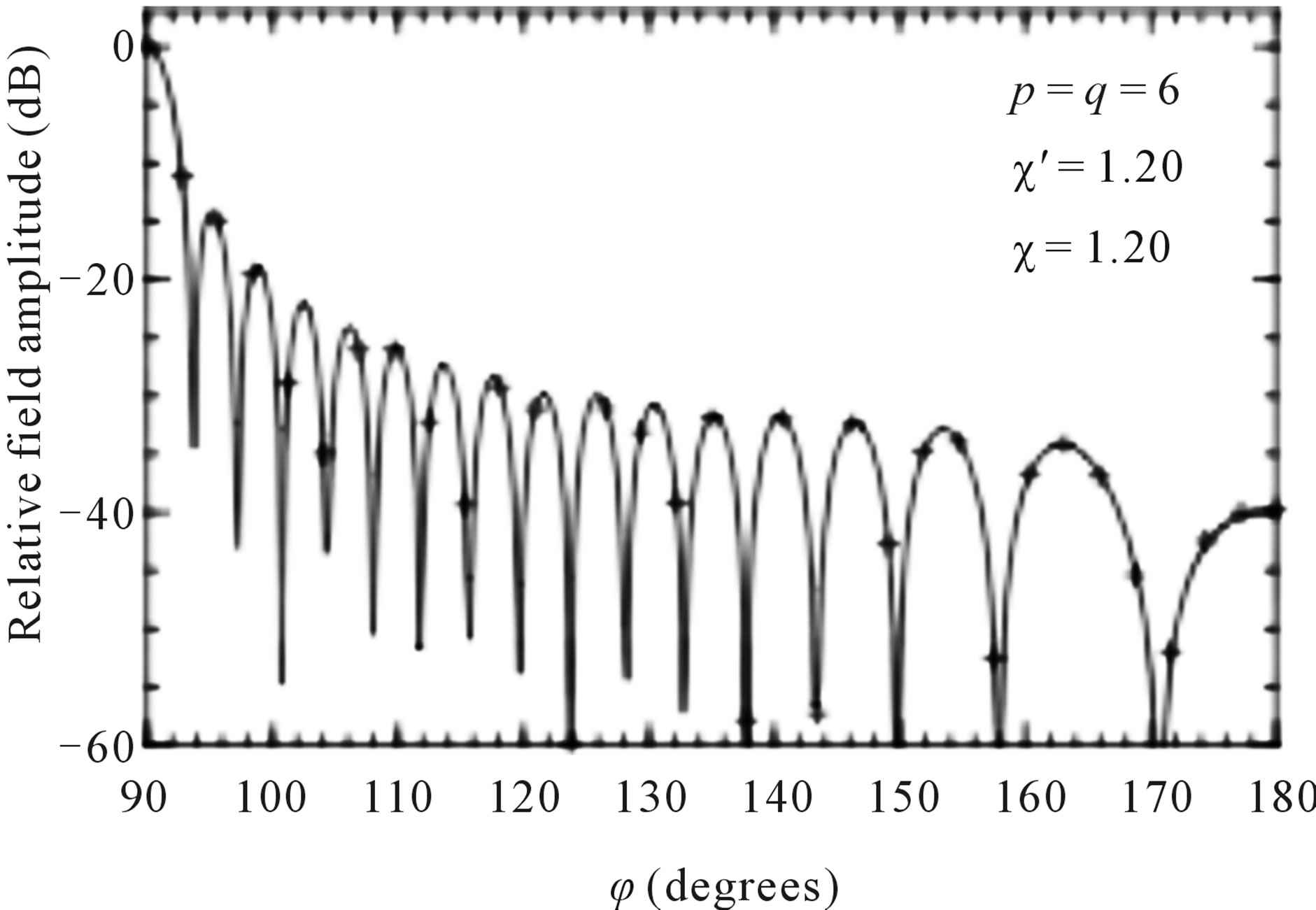
Figure 9. H-plane pattern. Solid line: exact. Crosses: reconstructed from nonuniform NF data.

Figure 10. Photo of the monopulse antenna.
a' = 4.2 cm. The helix lies on a cylinder with d = 17.5 cm and h = 240 cm. To assess the effectiveness of the technique in severe conditions as in the case of measurements performed by using bad positioning systems, we have enforced the acquisition of the NF data in such a way that the distances in x and h between the position of each nonuniform sample and the associate uniform helicoidal one are random variables uniformly distributed in  and
and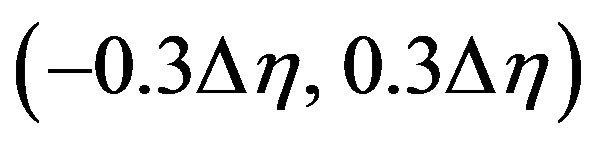 . It is worth noting that no optical device has been used to read the actual sampling positions, since those given by the employed positioners were more than safe.
. It is worth noting that no optical device has been used to read the actual sampling positions, since those given by the employed positioners were more than safe.
The amplitude and phase of the probe voltage relevant to the generatrix at j = 0˚ reconstructed by using 10 iterations are compared in Figures 11 and 12 with those directly measured. According to Figure 6, such a number of iterations ensures the algorithm convergence with very low errors. Note that the phase is shown only in the range [–20 cm, 120 cm] to improve the readability. As can be seen, although the considered positioning errors are very pessimistic in an actual scanning procedure, there is an excellent agreement between the recovered voltage and the measured one, save for the peripheral zone wherein the error is caused both by the truncation of the scanning area and by the environmental reflections. The smoother behaviour of the reconstructed voltage with respect to the measured one is due to the filtering properties of the interpolation functions which cut away the spatial harmonics of the noise sources outside the AUT spatial bandwidth.
At last, the FF patterns in the principal planes E and H recovered from the irregularly spaced helicoidal NF data are compared in Figures 13 and 14 with those (references) obtained from the data directly measured on the classical cylindrical grid. In both the cases, the software package MI-3000 has been used to get the FF reconstructions. Obviously, once the uniform data have been retrieved, the OSI algorithm has been used to recover the cylindrical data needed to carry out the NF-FF transformation.
Note that all the reported reconstructions have been obtained by using ,
,  , and p = q = 6.
, and p = q = 6.
It is interesting to compare the number of acquired nonuniform NF data (1512) with that (5760) required by the traditional cylindrical and helicoidal scanning techniques [14] to cover the same measurement zone.
6. Conclusions
An effective iterative technique for compensating the probe positioning errors in the NF-FF transformation with helicoidal scanning using a cylinder ended in two
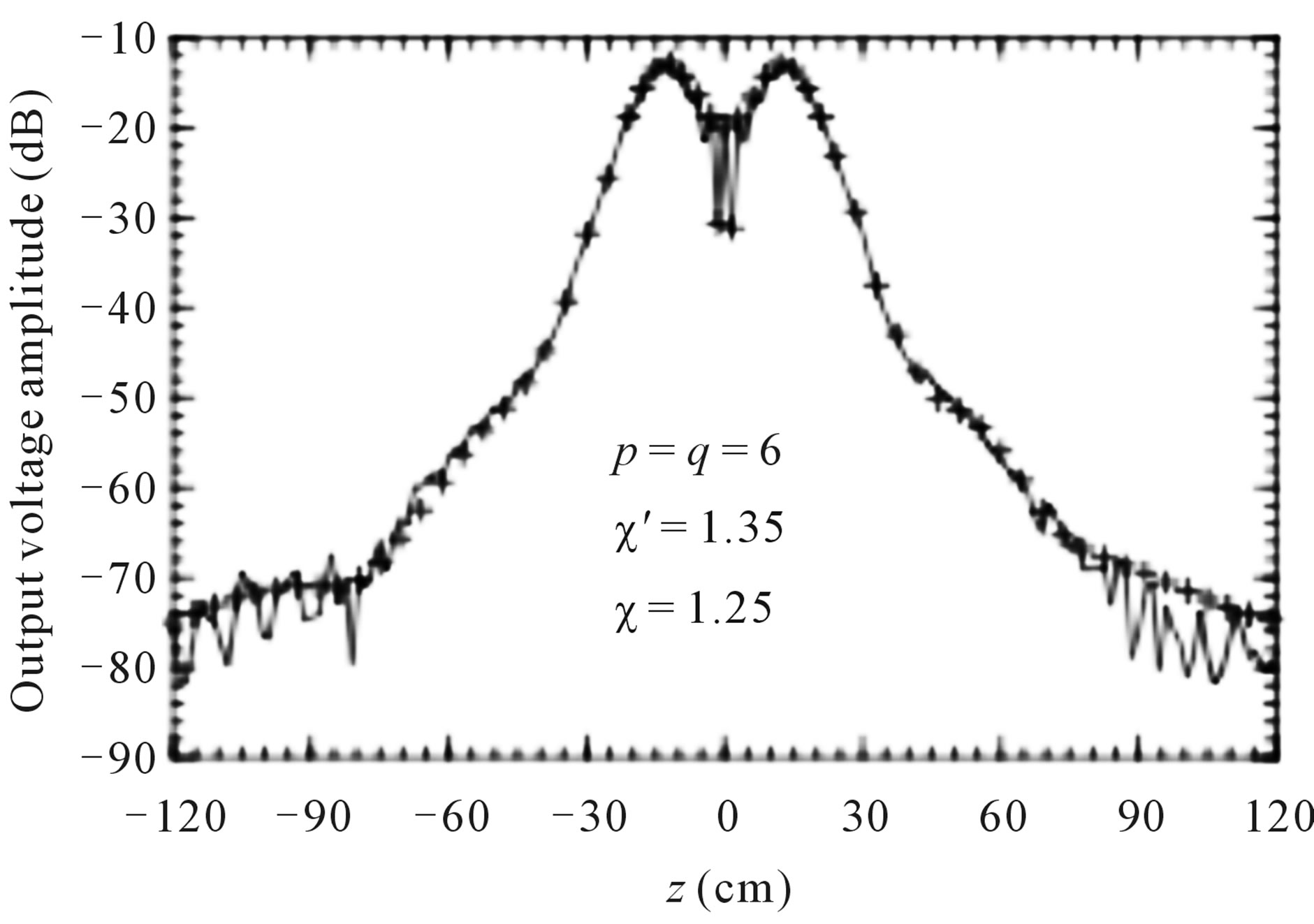
Figure 11. Amplitude of the probe voltage on the generatrix at φ = 0˚. Solid line: measured. Crosses: recovered from irregularly spaced NF data.
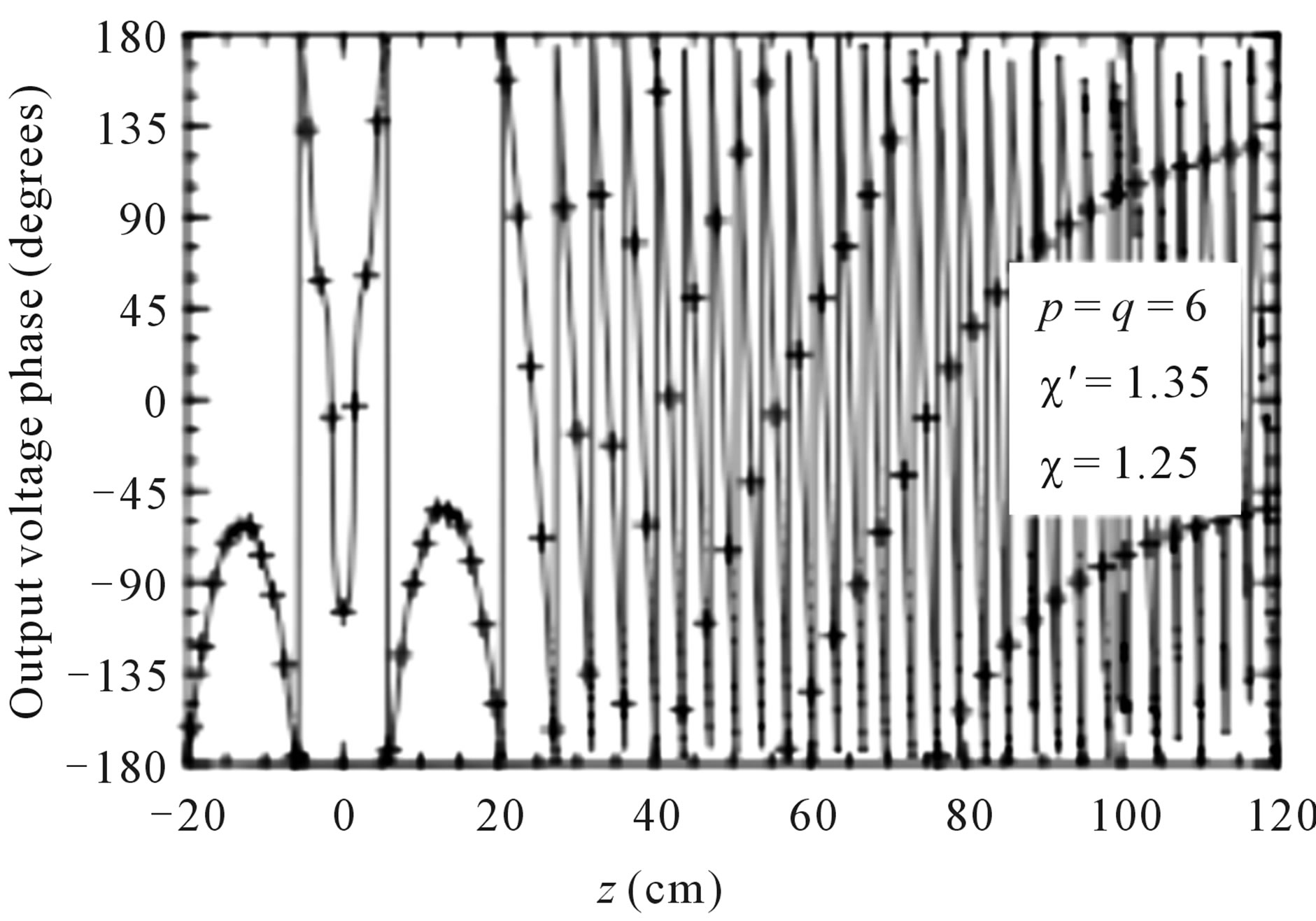
Figure 12. Phase of the probe voltage on the generatrix at φ = 0˚. Solid line: measured. Crosses: recovered from irregularly spaced NF data.
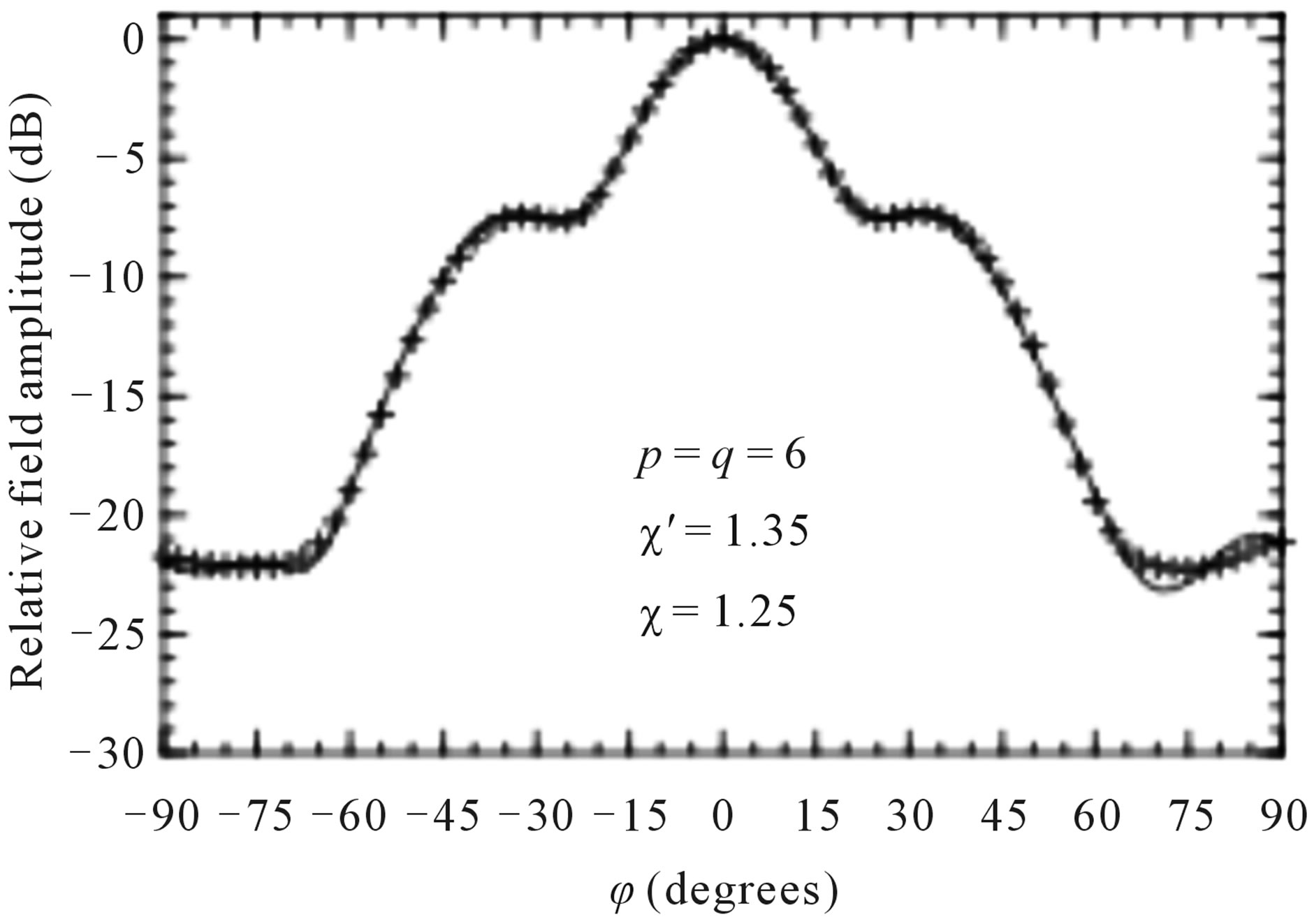
Figure 13. E-plane pattern. Solid line: reference. Crosses: recovered from irregularly spaced NF data.
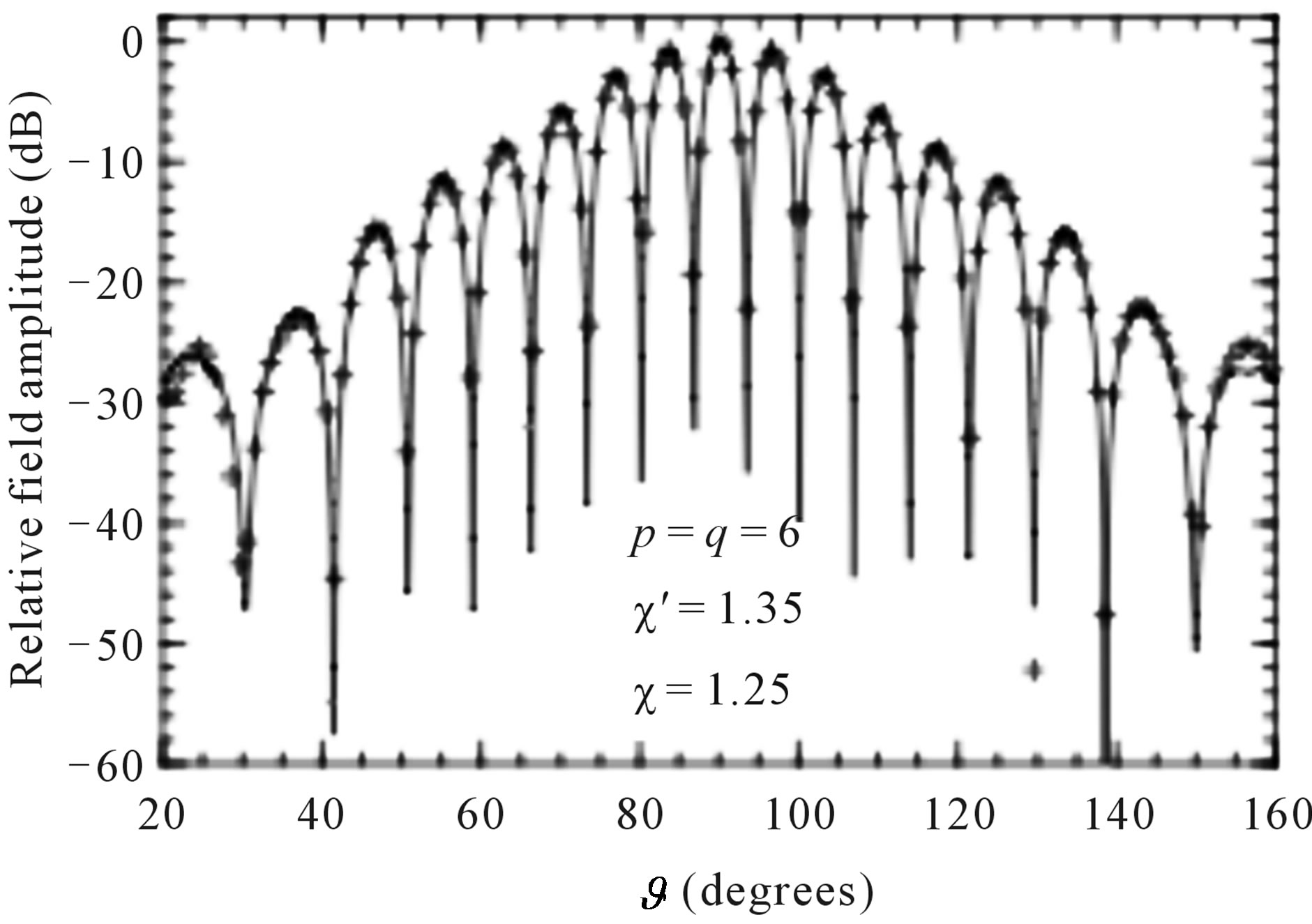
Figure 14. H-plane pattern. Solid line: reference. Crosses: recovered from irregularly spaced NF data.
half-spheres to model an electrically long antenna has been here proposed. In particular, the helicoidal NF data at the points fixed by the sampling representation are efficiently reconstructed from the acquired irregularly spaced ones, whose positions are known. Once the helicoidal data have been retrieved, those needed by a classical NF-FF transformation with cylindrical scanning are efficiently evaluated via the two-dimensional OSI algorithm. The effectiveness of the approach has been assessed both numerically and experimentally.
REFERENCES
- R. G. Yaccarino, L. I. Williams and Y. Rahmat-Samii, “Linear Spiral Sampling for the Bipolar Planar Antenna Measurement Technique,” IEEE Transactions on Antennas and Propagation, Vol. AP-44, No. 7, 1996, pp. 1049- 1051. doi:10.1109/8.504314
- O. M. Bucci, C. Gennarelli, G. Riccio and C. Savarese, “Nonredundant NF-FF Transformation with Helicoidal Scanning,” Journal of Electromagnetic Waves and Applications, Vol. 15, No. 11, 2001, pp. 1507-1519. doi:10.1163/156939301X00076
- O. M. Bucci, F. D’Agostino, C. Gennarelli, G. Riccio and C. Savarese, “Probe Compensated FF Reconstruction by NF Planar Spiral Scanning,” IEE Proceedings, Microwaves Antennas and Propagation, Vol. 149, No. 2, 2002, pp. 119-123. doi:10.1049/ip-map:20020265
- O. M. Bucci, F. D’Agostino, C. Gennarelli, G. Riccio and C. Savarese, “NF-FF Transformation with Spherical Spiral Scanning,” IEEE Antennas and Wireless Propagation Letters, Vol. 2, 2003, pp. 263-266. doi:10.1109/LAWP.2003.820710
- F. D’Agostino, C. Gennarelli, G. Riccio and C. Savarese, “Theoretical Foundations of Near-Field-Far-Field Transformations with Spiral Scannings,” Progress in Electromagnetics Research, Vol. PIER 61, 2006, pp. 193-214. doi:10.2528/PIER06021401
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero and M. Migliozzi, “Near-Field-Far-Field Transformation Technique with Helicoidal Scanning for Elongated Antennas,” Progress in Electromagnetics Research B, Vol. 4, 2008, pp. 249-261. doi:10.2528/PIERB08011503
- F. D’Agostino, F. Ferrara, J. A. Fordham, C. Gennarelli, R. Guerriero, M. Migliozzi, G. Riccio and C. Rizzo, “An Effective NF-FF Transformation Technique for Elongated Antennas Using a Fast Helicoidal Scan,” IEEE Antennas and Propagation Magazine, Vol. 51, No. 4, 2009, pp. 134-141. doi:10.1109/MAP.2009.5338700
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero and M. Migliozzi, “Laboratory Tests Assessing the Effectiveness of the NF-FF Transformation with Helicoidal Scanning for Electrically Long Antennas,” Progress in Electromagnetics Research, Vol. PIER 98, 2009, pp. 375-388. doi:10.2528/PIER09092303
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero and M. Migliozzi, “An Effective NF-FF Transformation Technique with Planar Spiral Scanning Tailored for QuasiPlanar Antennas,” IEEE Transactions on Antennas and Propagation, Vol. 56, No. 9, 2008, pp. 2981-2987. doi:10.1109/TAP.2008.928786
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero, M. Migliozzi and G. Riccio, “A Nonredundant Near-Field to Far-Field Transformation with Spherical Spiral Scanning for Nonspherical Antennas,” The Open Electrical & Electronic Engineering Journal, Vol. 3, 2009, pp. 1-8. doi:10.2174/1874129000903010001
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero, and M. Migliozzi, “The Unified Theory of Near-FieldFar-Field Transformations with Spiral Scannings for Nonspherical Antennas,” Progress in Electromagnetics Research B, Vol. 14, 2009, pp. 449-477. doi:10.2528/PIERB09031808
- O. M. Bucci, C. Gennarelli and C. Savarese, “Representation of Electromagnetic Fields over Arbitrary Surfaces by a Finite and Nonredundant Number of Samples,” IEEE Transactions on Antennas and Propagation, Vol. 46, No. 3, 1998, pp. 351-359. doi:10.1109/8.662654
- O. M. Bucci, C. Gennarelli and C. Savarese, “Optimal Interpolation of Radiated Fields over a Sphere,” IEEE Transactions on Antennas and Propagation, Vol. AP-39, No. 11, 1991, pp. 1633-1643. doi:10.1109/8.102779
- S. Costanzo and G. Di Massa, “Far-Field Reconstruction from Phaseless Near-Field Data on a Cylindrical Helix,” Journal of Electromagnetic Waves and Applications, Vol. 18, No. 8, 2004, pp. 1057-1071. doi:10.1163/1569393042955414
- S. Costanzo and G. Di Massa, “Near-Field to Far-Field Transformation with Planar Spiral Scanning,” Progress in Electromagnetics Research, Vol. PIER 73, 2007, pp. 49-59. doi:10.2528/PIER07031903
- A. Dutt and V. Rohklin, “Fast Fourier Transforms for Nonequispaced Data,” Proceedings of SIAM Journal Scientific Computation, Vol. 14, No. 6, 1993, pp. 1369-1393.
- R. Wittmann, B. K. Alpert and M. H. Francis, “NearField Antenna Measurements Using Nonideal Measurement Locations,” IEEE Transactions on Antennas and Propagation, Vol. 46, No. 5, 1998, pp. 716-722. doi:10.1109/8.668916
- R. C. Wittmann, B. K. Alpert and M. H. Francis, “NearField, Spherical Scanning Antenna Measurements with Nonideal Probe Locations,” IEEE Transactions on Antennas and Propagation, Vol. 52, No. 8, 2004, pp. 2184- 2186. doi:10.1109/TAP.2004.832316
- O. M. Bucci, C. Gennarelli and C. Savarese, “Interpolation of Electromagnetic Radiated Fields over a Plane from Nonuniform Samples,” IEEE Transactions on Antennas and Propagation, Vol. AP-41, No. 11, 1993, pp. 1501- 1508. doi:10.1109/8.267349
- F. Ferrara, C. Gennarelli, G. Riccio and C. Savarese, “NF-FF Transformation with Cylindrical Scanning from Nonuniformly Distributed Data,” Microwave and Optical Technology Letters, Vol. 39, No. 1, 2003, pp. 4-8. doi:10.1002/mop.11109
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero and M. Migliozzi, “On the Compensation of Probe Positioning Errors When Using a Nonredundant Cylindrical NF-FF Transformation,” Progress in Electromagnetics Research B, Vol. 20, 2010, pp. 321-335. doi:10.2528/PIERB10032402
- G. H. Golub and C. F. Van Loan, “Matrix Computations,” J. Hopkins University Press, Baltimore, 1996.
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero, and M. Migliozzi, “Near-Field - Far-Field Transformation with Helicoidal Scanning from Irregularly Spaced Data,” International Journal of Antennas and Propagation, Vol. 2010, 2010, Article ID: 859396. doi:10.1155/2010/859396
- F. D’Agostino, F. Ferrara, C. Gennarelli, R. Guerriero and M. Migliozzi, “An Iterative Technique to Compensate for Positioning Errors in the NF-FF Transformation with Helicoidal Scanning for Long Antennas,” Progress in Electromagnetics Research C, Vol. 18, 2011, pp. 73-86. doi:10.2528/PIERC10102801
- W. M. Leach Jr. and D. T. Paris, “Probe Compensated Near-Field Measurements on a Cylinder,” IEEE Transactions on Antennas and Propagation, Vol. AP-21, No. 4, 1973, pp. 435-445. doi:10.1109/TAP.1973.1140520
- O. M. Bucci, G. D’Elia and M. D. Migliore, “Advanced Field Interpolation from Plane-Polar Samples: Experimental Verification,” IEEE Transactions on Antennas and Propagation, Vol. 46, No. 2, 1998, pp. 204-210. doi:10.1109/8.660964

