ABSTRACT

We derive a general form of the induced electromotive force due to a time-varying magnetic field. It is shown that the integral form of Faraday’s law of induction is more conveniently written in the covering space. Thus the differential form is shown to relate the induced electric field in the n^th winding number to the (n+1)^th time-derivative of the magnetic field.

1. Introduction

Faraday’s law of induction in its differential and integral forms is a well-known standard topic which is discussed in many textbooks on electricity and magnetism [1-4]. Its integral form relates the closed line integral of the induced electric field to the negative time-derivative of the enclosed magnetic flux. This induced electric field creates an induced electromotive force which gives a magnetic field that, by Lenz’s law, opposes the change in the magnetic flux. Therefore the magnetic field is modified each time the path is traversed. A consequence of this is that the induced electromotive force (ε) is a sum over all contributions of multiple paths. The role of multiple paths in determining the final outcome was suggested long time ago by Feynman in his path integral method [5]. There have been several applications of the path integral method in various fields. For example, in the discussion of the Aharonov-Bohm effect [6], in nonlinear filtering [7], in proton-transfer reactions [8], in the study of vibrational and rotational free energies of hydrated Chloride ions [9] and in atomic interferometry [10]. A convenient way in the treatment of such problems is the use of a covering space as proposed long ago by Schulman [11]. 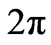In the covering space, the two-dimensional polar angle, θ ranges from to +∞ rather than 0 to in the physical space. The usefulness of a covering space in the discussion of multiple paths was utilized by several authors [12-14].The purpose of this work is to consider the consequences of a rather straight forward and more fundamental problem, for which the solution on the covering space can be written down. In particular, we derive a general form of the induced electromotive force due to a time-varying magnetic field. Thereafter, the integral form of Faraday’s law of induction is necessarily written on the covering space and the differential form relates the induced electric field for the n^th loop (the so-called winding number) to the (n + 1)^th time-derivative of the magnetic field. In section 2, we consider a time-varying magnetic field in a circuit and derive the induced electromotive force, ε. In section 3, we show how we can write the integral and differential forms of Faraday’s law of induction on the covering space. Section 4 is devoted for discussion and conclusion.

2. Derivation of the Induced Electromotive Force, emf

Consider an external time-varying magnetic field that passes through a circuit of resistance R. We derive the induced electromotive force (emf = ε) by the method of successive approximation. First, we pretend that the magnetic field is, and the emf is given by the negative rate of change of the magnetic flux as

, (1)

and thus the induced current is

. (2)

This induced current generates a magnetic field of its own, , whose direction is such that, by Lenz’s law, to oppose the change in the magnetic flux. Biot-Savart law ensures that this magnetic field can be written as

, (3)

where 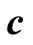is a vector whose magnitude depends on the geometry of the circuit. In the second step of the approximation, the total magnetic field through the circuit is

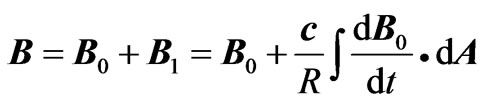, (4)

and thus, using Equation (1), the modified emf at the end of this step is

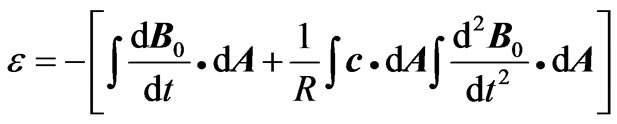. (5)

The above emf gives rise to a modified current given by

, (6)

which in turn generates its own magnetic field, 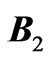given by

, (7)

where the prime denotes time derivative.

In the third step of the approximation, the total magnetic field that passes through the circuit is

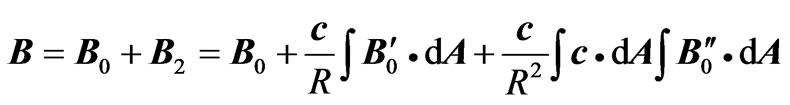, (8)

which corresponds to another modified emf given by

(9)

In a similar manor, it is easy to show that the modified emf at the end of the fourth step of approximation is

(10)

where is the 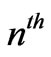time-derivative of the magnetic field. Therefore, carrying the above steps further, one finds that the general formula for the emf is

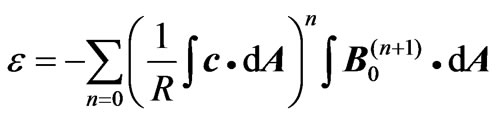. (11)

It is instructive to write Equation (11) in terms of the self-inductance, of the circuit which is defined as

, (12)

so the result is

. (13)

The above equation shows that the induced electromotive force is written as a power series of self-inductance of the circuit and surface integrals over higher time-derivatives of the external magnetic field,. One may easily check that the term in the sum in Equation (13) has the expected unit, volt. Furthermore, the first term in the sum () gives the induced emf that is found in most standard electromagnetic textbooks [4], namely

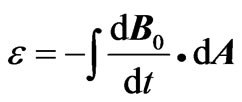. (14)

3. Integral and Differential Forms of Faraday’s Law

The term of Equation (13) contributes to the total induced emf a quantity given by

, (15)

and, as is well-known [4], this is accounted for by an induced electric field such that

. (16)

This may be viewed as a closed line integral around the 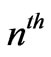loop (winding number) in the covering space whose polar angle. The necessity for a covering space was emphasized long time ago by AL-Jaber and Henneberger [12]. Therefore, the integral form of Faraday’s law in the covering space is

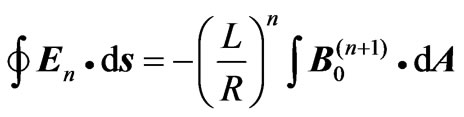, (17)

which gives the loop (winding number n) contribution to the induced electric field due to the 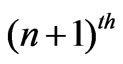time-derivative of the magnetic field. In the physical space, where the polar angle, one has to add all contributions coming from different loops (winding numbers) to get the induced electric field, namely

. (18)

The above equation gives the integral form of Faraday’s law. It must be noticed that the closed line integral on is carried out on the physical space, while the closed line integral on the right is carried out on the covering space. The differential form of Faraday’s law is readily obtained by applying Stoke’s theorem to convert a closed line integral into a surface integral. In the covering space, one immediately gets

, (19)

while in the physical space, the result is

. (20)

The case n = 0 is readily obtained from the above two equations with the result

, (21)

which is a well-known result.

4. Conclusions and Discussion

In this paper, we derived a general form of the induced electromotive force using the method of successive approximation. It was shown that this induced electromotive force is a power series of the self-inductance of the circuit and of surface integrals of higher time-derivatives of the external magnetic field. The first term in the series is the familiar induced electromotive force and the higher order terms are contributions coming from different winding numbers in the covering space. The 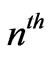term in the series is accounted for by the closed line integral of an induced electric field around the loop (winding number) in the covering space. Therefore, the integral form of Faraday’s law was written in the covering space and the contribution coming from the winding number is proportional to the power of self-inductance and to the surface integral of the 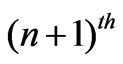timederivative of the external magnetic field. In addition, the differential form of Faraday’s law relates the curl of the induced electric field coming from the winding number to the 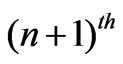time-derivative of the external magnetic field. While in the physical space, the curl of the total induced electric field is related to the sum of all contributions coming from different winding numbers.

REFERENCES